-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Condensed Matter Physics
p-ISSN: 2163-1115 e-ISSN: 2163-1123
2014; 4(4): 71-77
doi:10.5923/j.ajcmp.20140404.02
Elliott Model for Optical Absorption by Exciton and Two-Photon Absorption in Zinc Borophosphate Glasses
Fouad El-Diasty1, F. A. Abdel Wahab1, Manal Abdel-Baki2, Safeya Ibrahim2
1Physics department, Faculty of Science, Ain Shams University, Abbasia, Cairo, Egypt
2Glass Department, National Research Centre, Dokki, Giza, Egypt
Correspondence to: Fouad El-Diasty, Physics department, Faculty of Science, Ain Shams University, Abbasia, Cairo, Egypt.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
A series of ternary phosphate glass system, required for IR photonic applications, is synthesized by the melt-quenching technique. The effect of replacing ZnO (divalent) with Na2O (monovalent) on some optoelectronic properties of the prepared glass system, such as band gap energy and exciton-phonon coupling, is investigated. The dependence of composition on the two-photon absorption coefficient is inferred over a wavelength range of 0.2-2.5 μm. The exciton excitation mechanism is discussed by applying Elliott’s model which indicates a direct electronic interband transition. Chemical bond approach is applied to analyze and explain the obtained results and their effect on the glass properties.
Keywords: Two-photon absorption coefficient, Optoelectronic properties, Elliott’s model
Cite this paper: Fouad El-Diasty, F. A. Abdel Wahab, Manal Abdel-Baki, Safeya Ibrahim, Elliott Model for Optical Absorption by Exciton and Two-Photon Absorption in Zinc Borophosphate Glasses, American Journal of Condensed Matter Physics, Vol. 4 No. 4, 2014, pp. 71-77. doi: 10.5923/j.ajcmp.20140404.02.
Article Outline
1. Introduction
- Intrinsic optical properties of a glass used in optoelectronic devices are determined by two basic physical processes; UV- interband electronic transitions (band gap energy) and lattice vibrations (or phonons). However, interband transitions are from the upper anion valence band of oxygen (2p6) to the conduction band of cation (3s + 3d). According to electronic polarization theory, bound electrons oscillate at a frequency proportional to the square root of the binding energy divided by the electronic mass. Furthermore, oscillator strength is proportional to the inverse of binding energy. Therefore glasses with light atoms and strong bonding would have a large band gap, hence high UV transmission. High bonding energy (high-energy band gap) means low refractive index. On the other hand, absorption at the infrared edge (multiphonon absorption) of glass is mainly caused by anharmonic terms in the lattice potential leading to higher harmonics of lattice resonances; lattice vibrations (phonons). Since the experimental observation for two-photon absorption (TPA) by Kaiser and Garrett [1] and the nonlinear optical phenomenon is used to describe transition from ground state to an excited one by the simultaneous absorption of two laser photons. In the process, the atomic transition rate R is given by:
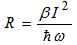 | (1) |
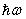 is the photon energy. Optical glasses with a large nonlinear absorption coefficient are promising materials for devices such as ultrafast power limiters.Phosphate glasses which include large amounts of d0 transition or empty d-block elements are of interest for photonic technological applications. For instance, amorphous phosphate sp3 hybrid orbitals are formed by the p-orbital electrons (3s23p3). The 5th electron is promoted to a 3d orbital where strong π-bonding molecular orbitals are formed with oxygen 2p electrons. These tetrahedra link through covalent bridging oxygens form various phosphate anions (v-P2O5). Due to low dispersion and relatively high refractive indices compared with silicate glasses, the phosphate glasses could be used as achromatic host materials in solid state lasers [2]. Borophosphate glasses with Raman vibrations up to 1300 cm-1 (equivalent to almost 50 THz of bandwidth) exhibit broad Raman bandwidth and flat gain broadband amplification [3].Sodium-borophosphate glass matrices are of interest for many applications such as hosts for rare-earth dopants needed for fiber amplifiers [4]. Zinc borophosphate glass is used for white LED and for second harmonic generation [5, 6]. Zinc borophosphate glass is a good host dielectric matrix for semiconductor quantum dots, therefore is used for optoelectronics and nonlinear applications [7]. Sodium zinc phosphate glasses are of practical interest as good hosts for laser applications [8]. Due to its high electro-optical Kerr effect and hence its large third-order nonlinearity [9, 10] sodium-borophosphate glass was applied for Bragg gratings production [11].As discussed previously, sodium zinc borophosphate glasses are indispensable materials for many fields such as microelectronics, lasers and infrared technology. In spite the chemical structure of these types of glasses are extensively studied [12], the effect of modifiers oxidation states on optoelectronic structure of the glass are poor investigated. In previous a work [13] we have attempted fabrication of sodium zinc borophosphate glass, which is suitable for IR photonic devices, and characterized its dispersion as well. In this context, the present study is designed to investigate the effect of the replacement of MO-type (ZnO) modifying oxide by M2O-type oxide (Na2O) on the linear and nonlinear absorption mechanisms of borophosphate glasses for optical limiting applications.
is the photon energy. Optical glasses with a large nonlinear absorption coefficient are promising materials for devices such as ultrafast power limiters.Phosphate glasses which include large amounts of d0 transition or empty d-block elements are of interest for photonic technological applications. For instance, amorphous phosphate sp3 hybrid orbitals are formed by the p-orbital electrons (3s23p3). The 5th electron is promoted to a 3d orbital where strong π-bonding molecular orbitals are formed with oxygen 2p electrons. These tetrahedra link through covalent bridging oxygens form various phosphate anions (v-P2O5). Due to low dispersion and relatively high refractive indices compared with silicate glasses, the phosphate glasses could be used as achromatic host materials in solid state lasers [2]. Borophosphate glasses with Raman vibrations up to 1300 cm-1 (equivalent to almost 50 THz of bandwidth) exhibit broad Raman bandwidth and flat gain broadband amplification [3].Sodium-borophosphate glass matrices are of interest for many applications such as hosts for rare-earth dopants needed for fiber amplifiers [4]. Zinc borophosphate glass is used for white LED and for second harmonic generation [5, 6]. Zinc borophosphate glass is a good host dielectric matrix for semiconductor quantum dots, therefore is used for optoelectronics and nonlinear applications [7]. Sodium zinc phosphate glasses are of practical interest as good hosts for laser applications [8]. Due to its high electro-optical Kerr effect and hence its large third-order nonlinearity [9, 10] sodium-borophosphate glass was applied for Bragg gratings production [11].As discussed previously, sodium zinc borophosphate glasses are indispensable materials for many fields such as microelectronics, lasers and infrared technology. In spite the chemical structure of these types of glasses are extensively studied [12], the effect of modifiers oxidation states on optoelectronic structure of the glass are poor investigated. In previous a work [13] we have attempted fabrication of sodium zinc borophosphate glass, which is suitable for IR photonic devices, and characterized its dispersion as well. In this context, the present study is designed to investigate the effect of the replacement of MO-type (ZnO) modifying oxide by M2O-type oxide (Na2O) on the linear and nonlinear absorption mechanisms of borophosphate glasses for optical limiting applications.2. Experimental
2.1. Glass Preparation
- Series of sodium zinc borophosphate glasses of the compositions xNa2O−(0.5−x)ZnO−0.1B2O3−0.4P2O5 with 0 ≤ x ≤ 0.4 mol fraction are prepared. The used materials were of chemically pure grade, in the form of H3BO3, Na2CO3, 2[NH4H2PO4] and ZnO. The amount of the glass batch was 50 g melt-1. The glass is prepared by melt quenching technique using platinum 2% rhodium crucibles in an electric furnace. The batch was pre-heated at 500-600℃ for almost an hour to evaporate the carbonates. The temperature of melting was 900-1100℃, the duration of melting was one hour after the last traces of batches were disappeared. To avoid the presence of bubbles the glasses were continue stirred during the glass melt preparation. Then the melt was poured onto stainless steel mould and annealed at around 350℃ to remove the thermal strains. Optical slabs were prepared by grinding and polishing of the prepared samples with paraffin oil and minimum amount of water. The thickness of the glass slabs was about 3 mm. Polishing method was completed with stannic oxide and paraffin to reach a surface roughness less than λ/3, which was tested by interferometric method. The homogeneity of the glasses was examined using two crossed polarizers.
2.2. Spectrophotometric Measurements
- Computer aided two-beam spectrophotometer (shimadzu-3101PC UV-VIS NIR) was used to record the reflectance, R, and the transmittance, T, data of the slab plane-parallel glass samples. A resolution limit of 0.2 nm and a sampling interval of 2 nm were utilized for the different 1401 measuring points. The uncertainty of measuring R(λ), and T (λ) is ±0.003 with the incident beam making an angle of 5.0°± 0.1° to the normal to the external slab faces. The measurements were carried out at room temperature for the spectral range 0.2-2.5 μm.
3. Results
3.1. Optical Band Gap Parameters Measurement
- Glass with low band gap energy, Eg, and thus high refractive index has advantageous for strong optical field confinement which allows standard waveguide bend radii. It also enhances the optical performance of photonic-crystals through efficient nonlinear interactions [14]. Using the measured transmittance T and reflectance R, and according to Beer-Lambert law, the absorption coefficient, α, (in cm-1) of the investigated glass system is calculated by:
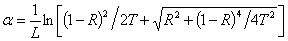 | (2) |
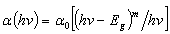 | (3) |
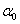 is a temperature independent constant related to the extent of the band tailing. The obtained values of the direct, Egd, and indirect, Egind, band gap energies using Eq. (3) are listed in Table 1, where Fig. 1 shows, for example, the calculation of direct band gap energy of sample 1.
is a temperature independent constant related to the extent of the band tailing. The obtained values of the direct, Egd, and indirect, Egind, band gap energies using Eq. (3) are listed in Table 1, where Fig. 1 shows, for example, the calculation of direct band gap energy of sample 1.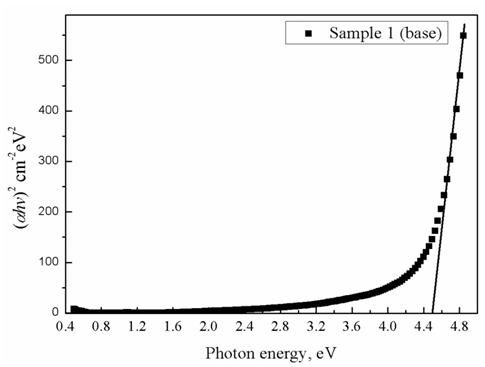 | Figure 1. Direct bandgap calculation, sample 1 is taken as an example |
3.2. Nonlinear Absorption for Photonic Applications
- Two-photon absorption (TPA) implies that two light quanta (two photons) must be absorbed simultaneously, so the excitation mechanism can be done through nonlinearly allowed electric-dipole transition. Two-photon absorption coefficient (in units of cm/GW) is determined from the obtained optical band gap Eg of the glass. The two-photon absorption coefficient is given by [17]:
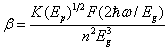 | (4) |
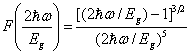 | (5) |
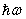 is less than the band gap energy Eg but greater than Eg /2.
is less than the band gap energy Eg but greater than Eg /2.3.3. Elliott Model for Interband Absorption by Excitons
- Optical absorption described by Tauc’s model [15, 20] for interband transitions assumes; (1) neglected contributions from heavy and light holes, (2) the matrix element is momentum independent, and (3) no bounded electron-hole pair (exciton) or electron-impurity interactions are included. Moreover, formation of excitons increases the optical transition rate. Regarding exciton model for optical response, Elliott [21] provided an expression for optical absorption in terms of effective exciton Rydberg. The Elliott model adopts: (1) parabolic bands and (2) transition momentum matrix elements between single-particle states are constant throughout the Brillouin zone. Considering a hydrogen-atom-like structure of exciton with negligible center-of-mass kinetic energy, the excited states of an exciton is given by:
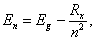 | (6) |
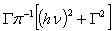 . The expression which is used to analyze the optical properties is given by [23, 24]:
. The expression which is used to analyze the optical properties is given by [23, 24]: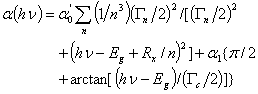 | (7) |
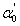 represents the absorption peak at ground state exciton energy and
represents the absorption peak at ground state exciton energy and 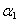 is the absorption at band gap. Also, Γn and Γc are the full-width at half maximum of Lorentzian and full-width of continuum excitons, and Rx the exciton binding energy. The higher values of the exciton quantum number n can be neglected due to n-3 dependence of the line intensity of excitons peak and thus n = 1 term is used in the summation of Eq. 7.
is the absorption at band gap. Also, Γn and Γc are the full-width at half maximum of Lorentzian and full-width of continuum excitons, and Rx the exciton binding energy. The higher values of the exciton quantum number n can be neglected due to n-3 dependence of the line intensity of excitons peak and thus n = 1 term is used in the summation of Eq. 7.4. Discussion
4.1. Optical Band Gap Energy
- According to Table 1, the band gap energy for the direct transition is 4.49 eV for sample 1 and 3.95 eV for sample 4. The equal molar fraction substitution of Na2O by ZnO led to a decrease in the glass band gap energy. The drop in the direct Eg reached 12.0 % with only 0.3 mole fraction of Na2O on expense of ZnO. For indirect interband transition the reduction in gap energy is 61.18 %, which depressing the glass band gap energy deeply to reach the direct semiconductor region. The molar mass of ZnO is 81.4084 g/mol while for Na2O is 61.97894 g/mol, so the replacement of sodium oxide by zinc oxide decreases the glass Eg with increasing Na2O content [13]. The inflection point observed with sample 5 for Eg may be attributed to P-O bond length change. Neutron diffraction studies indicate a decrease in the mean P–O bond length with increasing modifier field strength [25]. Since the field strength of the divalent modifier ion, Zn2+, is larger than that of the monovalent modifier ion Na+, so it is expected that with further increase for Na2O in place of ZnO content the mean P–O bond length increases and hence Eg decreases.The decrease in glass Eg can be explained taking into consideration that the basic units of pure amorphous borate glasses are trigonal BO3 groups, whereas the basic units of pure amorphous phosphate glasses are PO4 tetrahedra linked through covalent bridging oxygens. Therefore, addition of a modifier oxide to borate and phosphate networks has differing effects on the glass network and hence on alternation of the glass characteristics. In a borate network, the addition of a modifier oxide increases the degree of polymerization because the neutral trigonal BO3/2 groups are converted to nonbridging oxygen bonds (NBO) and tetrahedral
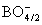 species owing to Lewis acid character of boron oxide. In the phosphate network, the addition of a modifier oxide has a depolymerizing effect; the extra oxygen atoms introduced by the modifier oxides form negative nonbridging oxygen sites, whose charge is compensated by positive charge of the modifier cations [26, 27].With addition of Na2O instead of ZnO, the value of glass molar polarization increased [13] and hence its band gap energy. The B3+ ion has 0.2
species owing to Lewis acid character of boron oxide. In the phosphate network, the addition of a modifier oxide has a depolymerizing effect; the extra oxygen atoms introduced by the modifier oxides form negative nonbridging oxygen sites, whose charge is compensated by positive charge of the modifier cations [26, 27].With addition of Na2O instead of ZnO, the value of glass molar polarization increased [13] and hence its band gap energy. The B3+ ion has 0.2  cation ionic radius and 0.003
cation ionic radius and 0.003 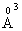 electronic polarizability, Na+ ion has 0.98
electronic polarizability, Na+ ion has 0.98 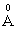 cation ionic radius and 0.181
cation ionic radius and 0.181 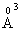 electronic polarizability, P5+ ion has 0.35
electronic polarizability, P5+ ion has 0.35 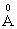 cation ionic radius and 0.0121
cation ionic radius and 0.0121 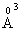 electronic polarizability, whereas the ionic radius of Zn2+ is 0.83
electronic polarizability, whereas the ionic radius of Zn2+ is 0.83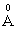 with 0.286
with 0.286 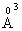 electronic polarizability [28]. The field strength of the divalent modifier ion, Zn2+, is 54.78
electronic polarizability [28]. The field strength of the divalent modifier ion, Zn2+, is 54.78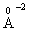 , which is more than that of the monovalent modifier ion Na+ (= 12.19
, which is more than that of the monovalent modifier ion Na+ (= 12.19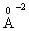 ). Thus, Zn2+ ion is more polarizable than Na+ ions. In the same time, with insertion of Na2O instead of ZnO the electronic polarizability of the oxygen ion increases [13]. So, as the ratio of Na2O/ZnO in the studied glasses composition changes the electronic polarizability of the oxygen ion changes as well, that describes the obtained behavior of the glass Eg.The overlap of atomic orbitals to form bands is an important effect that changes the band gap [29, 30]. Na2O is a direct band gap semiconductor could act as network modifier due to the relative large ionic radius of Na+ and its low field strength (in comparison to Zn2+) with spectra depend on the ligand field (crystal field effect). This concern suggests that both oxides enter in the glass in form of network modifiers, where the electronic shell of O2- ions is affected by the polarizing action of the modifying cations [31]. Thus conversion of covalent into ionic behavior of glass causes a decrease of Eg equivalent to semiconductor region. The s orbital energies for the alkali metals are quite high and their energetic overlap with the oxygen 2p orbitals is relatively poor. As consequence, these cations largely form ionic bonds with oxygen leading to a rapid decrease in Eg with the addition of Na2O. This behavior is associated with the facts that at higher Na2O content localized states are developed in the gap. This variation is due to increasing the influence of NBO ions with the increase in Na2O content. The large negative charges on NBO ions raise the top of the valance band resulting in the reduction of the glass optical energy gap [32].Since anionic atoms are more electronegative than cationic atoms, therefore the conduction band consists mainly of atomic orbitals of cationic atoms [33, 34]. Because oxygen has a higher electronegativity (3.5 eV) than sodium (0.93 eV), oxygen takes the electron from sodium. Since the difference in electronegativity (2.57 eV) is greater than 2.0 eV, then Na-O bond is an ionic bond which would decrease glass band gap. In case of zinc oxide, zinc has electronegativity 1.65 eV, so oxygen will share the binding electron with zinc pulling it closer to the oxygen atom forming a dipole. Because the difference in electronegativity of Zn-O bond is 1.85 eV, which is less than 2 eV, so a polar covalent bond is expected.
). Thus, Zn2+ ion is more polarizable than Na+ ions. In the same time, with insertion of Na2O instead of ZnO the electronic polarizability of the oxygen ion increases [13]. So, as the ratio of Na2O/ZnO in the studied glasses composition changes the electronic polarizability of the oxygen ion changes as well, that describes the obtained behavior of the glass Eg.The overlap of atomic orbitals to form bands is an important effect that changes the band gap [29, 30]. Na2O is a direct band gap semiconductor could act as network modifier due to the relative large ionic radius of Na+ and its low field strength (in comparison to Zn2+) with spectra depend on the ligand field (crystal field effect). This concern suggests that both oxides enter in the glass in form of network modifiers, where the electronic shell of O2- ions is affected by the polarizing action of the modifying cations [31]. Thus conversion of covalent into ionic behavior of glass causes a decrease of Eg equivalent to semiconductor region. The s orbital energies for the alkali metals are quite high and their energetic overlap with the oxygen 2p orbitals is relatively poor. As consequence, these cations largely form ionic bonds with oxygen leading to a rapid decrease in Eg with the addition of Na2O. This behavior is associated with the facts that at higher Na2O content localized states are developed in the gap. This variation is due to increasing the influence of NBO ions with the increase in Na2O content. The large negative charges on NBO ions raise the top of the valance band resulting in the reduction of the glass optical energy gap [32].Since anionic atoms are more electronegative than cationic atoms, therefore the conduction band consists mainly of atomic orbitals of cationic atoms [33, 34]. Because oxygen has a higher electronegativity (3.5 eV) than sodium (0.93 eV), oxygen takes the electron from sodium. Since the difference in electronegativity (2.57 eV) is greater than 2.0 eV, then Na-O bond is an ionic bond which would decrease glass band gap. In case of zinc oxide, zinc has electronegativity 1.65 eV, so oxygen will share the binding electron with zinc pulling it closer to the oxygen atom forming a dipole. Because the difference in electronegativity of Zn-O bond is 1.85 eV, which is less than 2 eV, so a polar covalent bond is expected. 4.2. Elliott Model for Optical Absorption by Excitons
- Optical absorption spectra recorded at room temperature of the present samples are fitted to Eq. (7) with
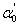 ,
, 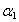 , Γ1, Γc, Eg, and Rx as adjustable parameters. Fig. 2 shows the representative fits to absorption spectra of sample 5 as an example. The disagreement observed at high energy side of the curve is due to a non-parabolic band effect [23]. The parameters obtained from the fit of absorption data of all samples are given in Table 1. It is clear that, the obtained values for gap energy using Elliot model,
, Γ1, Γc, Eg, and Rx as adjustable parameters. Fig. 2 shows the representative fits to absorption spectra of sample 5 as an example. The disagreement observed at high energy side of the curve is due to a non-parabolic band effect [23]. The parameters obtained from the fit of absorption data of all samples are given in Table 1. It is clear that, the obtained values for gap energy using Elliot model, 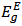 , [21] are close to those of direct transitions calculated in section 4.1 from the transmission spectra of the present glass compositions. Therefore, it is concluded that the direct electronic transition is the most probable transition in the present glass system. It should be noted that our findings exhibit small values of
, [21] are close to those of direct transitions calculated in section 4.1 from the transmission spectra of the present glass compositions. Therefore, it is concluded that the direct electronic transition is the most probable transition in the present glass system. It should be noted that our findings exhibit small values of 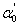 ,
, 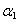 and Γc in comparison with previous studies on semiconducting thin films and single crystal materials [35-36]. This discrepancy could be attributed to the thermal history and amorphization degree of the studied samples. Moreover, exciton binding energy of the investigated glass is in the same order of magnitude as of semiconductor materials except that for the last two samples.
and Γc in comparison with previous studies on semiconducting thin films and single crystal materials [35-36]. This discrepancy could be attributed to the thermal history and amorphization degree of the studied samples. Moreover, exciton binding energy of the investigated glass is in the same order of magnitude as of semiconductor materials except that for the last two samples.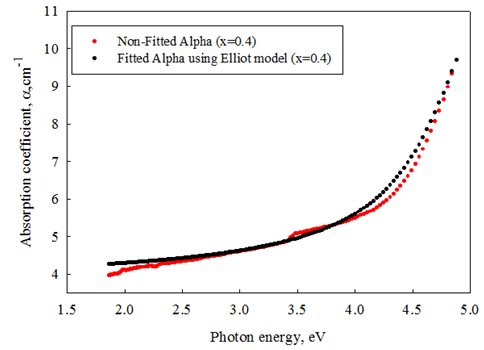 | Figure 2. Fitting routin for Elliot model with the fundamental absorption edge |
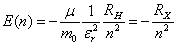 | (8) |
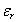 is the dielectric constant of the glass, RH is Rydberg constant of hydrogen atom (13.6 eV) and µ is the reduced mass. In addition the radius of the electron-hole orbit, rn, is given by:
is the dielectric constant of the glass, RH is Rydberg constant of hydrogen atom (13.6 eV) and µ is the reduced mass. In addition the radius of the electron-hole orbit, rn, is given by: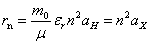 | (9) |
4.3. Nonlinear Absorption for Photonic Limiting Applications
- Glasses that exhibit a large nonlinear two-photon optical absorption (TPA) have enormous potential applications in photonic devices [38]. TPA puts crucial limitations on waveguide all-optical switching devices [39, 40]. Therefore, variation in nonlinear absorption coefficient or two-photon absorption coefficient, β, along with band gap energy, Eg, has been extensively studied [41-46]. The calculated dispersion of β versus photon energy (using Eqs.4 and 5) for the studied glass samples is shown in Fig. 3. Replacement of 0.3 mole fraction of Na2O by an equivalent molar fraction of ZnO enlarged the maximum value of nonlinear absorption coefficient from 1.66 cm/GW (sample 1, at 2.9 eV) to be 3.52 cm/GW (sample 4, at 2.59 eV). It means that nonbridging oxygen bonds have succeeded to increase the glass TPA coefficient by ≈ 112 % of its original value due to the obtained shrink in the glass band gap. Figure 3 shows also that the maximum value of β is shifted towards a lower energy as the molar fraction of NaO increases on the expense of ZnO (see Table 1). This enormous enhancement for TPA coefficient of glass is converted directly to enhance two-photon gain [47]. The obtained TPA coefficient of present glass is higher in magnitude than that reported for heavy bismuth and lead glasses [48-50]. Nevertheless, large free-carrier losses that limit the usable pump power for Raman amplification at telecommunication wavelengths is strongly overcome by the enhancement in two-photon emission [51, 52]. The gained results may open prospect for new two-photon amplifier devices and tunable laser technologies.
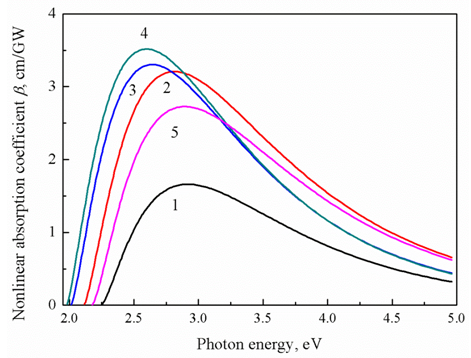 | Figure 3. Dispersion of two-photon absorption coefficient versus photon energy |
5. Conclusions
- The replacement of Na2O by ZnO in borophosphate glass increases the number of nonbridging oxygen bonds leading to a considerable shrink for the glass band gap. It means a robust control of TPA by tailoring glass band gap could be done through adjustment the Na2O to ZnO molar fraction ratio. Application of Elliot's model for the analysis of the fundamental absorption edge designated that the prepared glass has a direct interband transition mechanism. It explains the role of excitons on the calculated increase in two-photon absorption coefficient that is assisted by the existence of stable Frenkel excitons.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
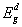 , and indirect,
, and indirect, 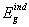 , band gap energies, fitting parameters for Elliot model including Elliot band gap,
, band gap energies, fitting parameters for Elliot model including Elliot band gap, 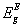 , values, exciton energy, Rx, and radius, rn, and temperature of exciton dissociation, and maximum value of two-photon absorption coefficient, βmax, and the corresponding photon energy, E, as function of composition for borophosphate glass samples
, values, exciton energy, Rx, and radius, rn, and temperature of exciton dissociation, and maximum value of two-photon absorption coefficient, βmax, and the corresponding photon energy, E, as function of composition for borophosphate glass samples