-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Condensed Matter Physics
p-ISSN: 2163-1115 e-ISSN: 2163-1123
2014; 4(4): 63-70
doi:10.5923/j.ajcmp.20140404.01
Electronic Structure Simulation of Aluminum Antimony Nanocrystal Using Ab-initio Density Functional Theorycoupled with Large Unit Cell Method
Akram Hashim Taha
Physics Dept., Faculty of Science and Health, Koya University, Erbil, Iraq
Correspondence to: Akram Hashim Taha, Physics Dept., Faculty of Science and Health, Koya University, Erbil, Iraq.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Ab-initio density functional theory (DFT) calculations coupled with large unit cell method (LUC) and using generalized gradient approximation (GGA)were carried out to simulate the electronic structure of AlSb nanocrystal for 8, 16, 54 and 64 core atoms. Results shows that the size of the core atoms effects on the electronic properties for a limited value of number of core atoms then most properties tends to behave more stable. The energy gap, lattice constant and total energy are inversely proportional with the number of core atoms. Significant result occurred that the energy gap of aluminum antimony nanocrystal drop to a very small value (0.03) eV at 54 core atoms and this amount of energy is in the range of conductor materials. The density of states increased with increasing of number of core atoms.
Keywords: Density functional theory, AlSb nanocrystals, Large unit cell, Ab-initio
Cite this paper: Akram Hashim Taha, Electronic Structure Simulation of Aluminum Antimony Nanocrystal Using Ab-initio Density Functional Theorycoupled with Large Unit Cell Method, American Journal of Condensed Matter Physics, Vol. 4 No. 4, 2014, pp. 63-70. doi: 10.5923/j.ajcmp.20140404.01.
1. Introduction
- Semiconductor nanocrystals of III-V compounds are of great significance due to their applications in various electronic and optical devices [1]. Rapid advances that have occurred in the preparation and characterization of nanocrystals, finally enables the studies of transformations between stable states of finite systems. Aluminum antimony (AlSb) seems to be a promising candidate for transistors and p-n junction diodes due to large band gap [2]. AlSb nanoclusters have also been synthesized by nanoscale electro deposition [3-5].Aluminum antimony (AlSb) has been ranked as one of the most promising materials for detection of γ-rayradiation at or near ambient temperatures [6]. Yee et al. [7] concluded that at room temperature AlSb should make an intrinsically better high-energy photon detector than CdTe, Si, and Ge. Applications with particular interest in such detectors include the interception and assessment of nuclear material in the field; nuclear-weapon control and disarmament (material protection, control, and accounting); the monitoring of nuclear-material processing; dismantling nuclear weapons; and remote unattended monitoring [8]. GaAs and In P both suffer from limited or inaccessible supplies of Ga and in thereby making the large-scale implementation of large arrays impossible. In considering materials availability, Al is one of the more abundantelements in the earth’s crust. Sb, while less abundant, is still considered common and is more abundant than As, Be, Bi, Cd, Te, and W. AlSb was originally a material system of great interest because of its potential applications inelectronic and photonic devices at high temperatures such as transistors, p–n junction diodes [7, 9, 10] and photovoltaic cells [6, 11, 12]. However, AlSb-based technologiesnever made any progress due to poor quality of surfaces that inhibits device processing and application. AlSb rapidly oxidizes when exposed to air, the growth of epitaxial layers and devices on AlSb substrates very difficult. Hence development of suitable chemical treatment of the wafer surface is crucial.AlSb crystal is used in a multitude of device applications, including light-emitting diodes (LEDs), lasers, detectors, and communication devices. It is also fabulous optical material, where it can be made to emit light efficiently, convert light energy into electrical energy, modulate the intensity of light and used as optical filters, mirrors, lenses, etc. [13]. Structural Phase Transition and the structural stability of lnm sized AlSb nanocrystal in its zinc blende (B3), rocksalt (Bl) and CsCl (B2) type phases under high compression of AISb Nanocrystal has been investigated by Neha et al. using density functional theory [14].Haider et al. studied the AlSb nanocrystals using restricted Hartree-Fock method [15]. In the present work we have used density functional theory formalism coupling with large unit cell method to investigate the electronic properties for AlSb nanocrystal for core atoms 8, 16, 54 and 64. The Slater Type Orbitals (STO) basis set is used in the calculation besides we have used unrestricted Hartree-Fock formalism. These calculations were carried out using the Gaussian 03 software package [16].
2. Theory
- The Schrödinger equation for one particle system can be solved simply, but it becomes more complicated for systems containing many particles. One of the most important goals of physics is to describe the physical properties of interacting many-particle systems. Such derivation requires the solution of the Schrödinger equation in 3N spatial variables and N spin variables.The Schrödinger equation of many body systems can be given by
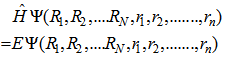 | (1) |
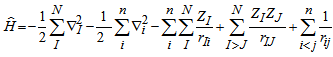 | (2) |
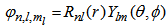 | (3) |
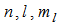 are the principal, azimuthal, and magnetic quantum numbers, respectively.The radial nodes, in practice, make little difference to the description of bounding, but considerably complicated the calculation of electron-electron repulsion integrals. Slater proposed a series of radial functions lacking nodes [20]:
are the principal, azimuthal, and magnetic quantum numbers, respectively.The radial nodes, in practice, make little difference to the description of bounding, but considerably complicated the calculation of electron-electron repulsion integrals. Slater proposed a series of radial functions lacking nodes [20]: 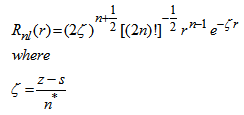 | (4) |
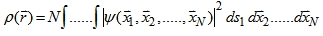 | (5) |
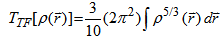 | (6) |
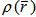 by using the classical expression for the nuclear-nuclear potential and electron-electron potential:
by using the classical expression for the nuclear-nuclear potential and electron-electron potential: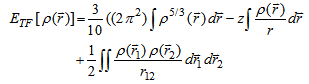 | (7) |
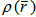 ]. So the total energy can be written as:
]. So the total energy can be written as: 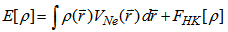 | (8) |
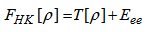 | (9) |
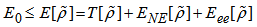 | (10) |
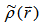 , which satisfies the necessary boundary conditions such as
, which satisfies the necessary boundary conditions such as 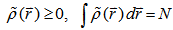 and associated with some external potential
and associated with some external potential 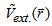 , the obtained energy from the functional of equation (7) represents the upper of the ground state energy E0. In 1965 Kohn-sham [26] derived two sets of differential equations enabling the ground state density
, the obtained energy from the functional of equation (7) represents the upper of the ground state energy E0. In 1965 Kohn-sham [26] derived two sets of differential equations enabling the ground state density 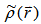 to be found. Kohn and Sham introduced the following separation of the functional F[ρ]:
to be found. Kohn and Sham introduced the following separation of the functional F[ρ]: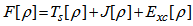 | (11) |
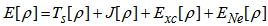 | (12) |
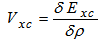 | (13) |
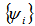 must be given, with the usual constraint
must be given, with the usual constraint 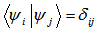 and using the variational principle we get the resulting equation which is known as Kohn-Sham equation:
and using the variational principle we get the resulting equation which is known as Kohn-Sham equation: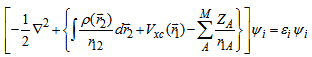 | (14) |
3. Results and Discussion
- The software used in the present work is the Gaussian 03 to simulate some of the properties of AlSb nanocrystal such as the optimized lattice constant, total energy, energy gap, etc… . The optimized value of 8, 16, 54 and 64 core atoms of AlSb nanocrystal have been calculated to find the minimum value of total energy (ground state) of each of these core atoms. Figure (1) shows the variation of total energy with lattice constant. The minimum energy means that the equilibrium point has been reached. Decreasing the distance between atoms leads to a decrease in the total energy, when the atoms become nearer to each other, the repulsive force will be the dominant. While at large distances the attractive force is the dominant. Stability of AlSb nanocrystal at equilibrium lattice constant is due to the equality of attractive and repulsive forces. Equilibrium lattice constant (aequ.) decreases as the number of core atoms increases. Results shows a good agreement with results recorded in Ref. [15]. For bulk AlSb the lattice constant is (0.6235) nm [27]. The aequ. for 8, 16, 54 and 64 AlSb core atoms were (0.6125, 0.6095, 0.603 and 0.6 nm) respectively. It is clear that the AlSb nanocrystal’s lattice constant tends to be close to the bulk value at small core atom.
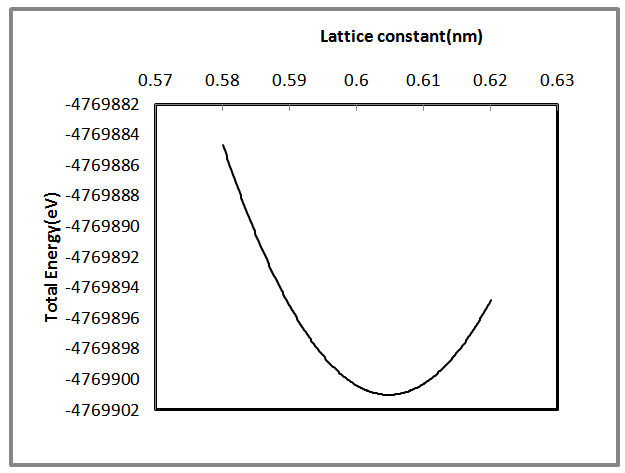 | Figure 1. Shows the total energy variation with lattice constant of 54 core atoms of AlSb nanocrystal |
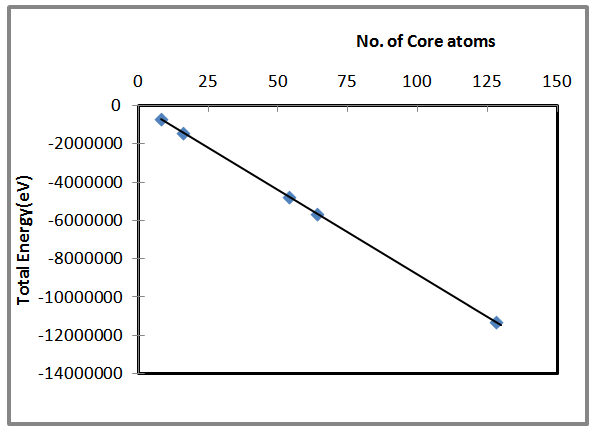 | Figure 2. Shows the total energy as a function of number of core atoms for AlSb nanocrystal |
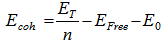
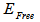 is the experimental free atom energy,
is the experimental free atom energy, 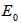 represents the correction to the cohesive energy for the zero-point motion of the nuclei [29] the theoretical value of the cohesive energy of bulk AlSb is (8.08 ev) according to Ahmed, et al [30] and experimentally Wyckoff found it to be (6.60eV) [31], while Aresti and Vermafount its experimental value to be (7.155 and 6.0245 eV) respectively [32, 33]. The calculated values in this work for AlSb nanocrystal for 8, 16, 54 and 64 core atoms was fluctuating about 6.90 eV see fig. (3).
represents the correction to the cohesive energy for the zero-point motion of the nuclei [29] the theoretical value of the cohesive energy of bulk AlSb is (8.08 ev) according to Ahmed, et al [30] and experimentally Wyckoff found it to be (6.60eV) [31], while Aresti and Vermafount its experimental value to be (7.155 and 6.0245 eV) respectively [32, 33]. The calculated values in this work for AlSb nanocrystal for 8, 16, 54 and 64 core atoms was fluctuating about 6.90 eV see fig. (3).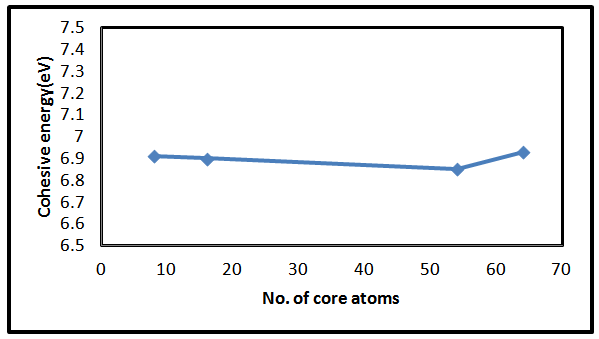 | Figure 3. The variation of cohesive energy Vs the number of core atoms for AlSb nanocrystal |
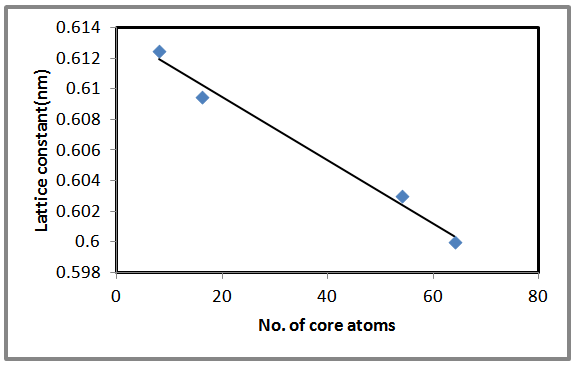 | Figure 4. The variation of the lattice constant with the number of core atoms for LUC AlSb nanocrystal |
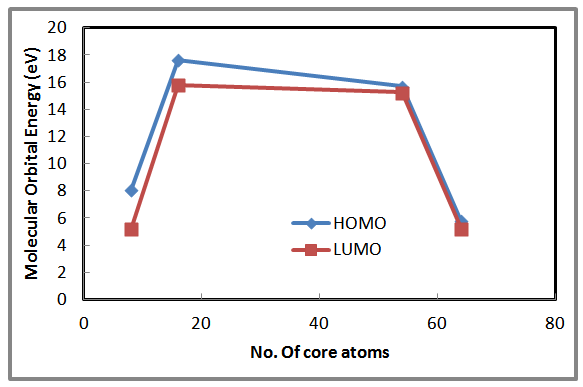 | Figure 5. Shows the HOMO and LUMO as a function of number of core atoms for AlSb nanocrystal |
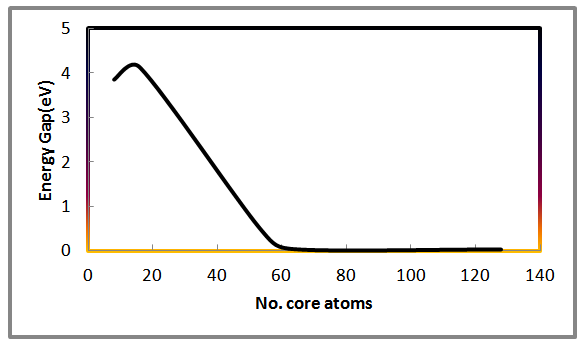 | Figure 6. Shows the variation of energy gap with the number of core atoms for AlSb nanocrystal |
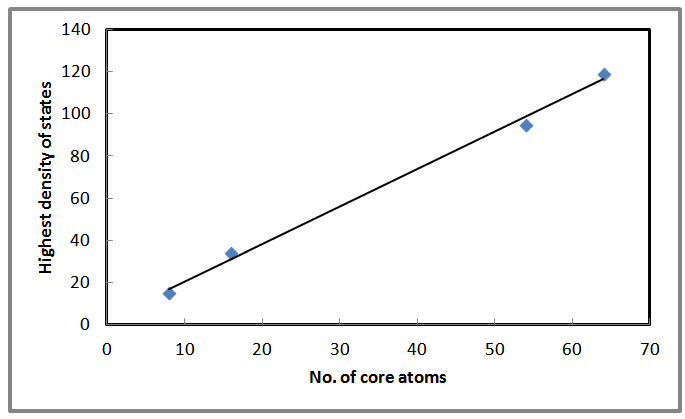 | Figure 7. Shows the highest density of states as a function of number of core atoms for AlSb nanocrystals |
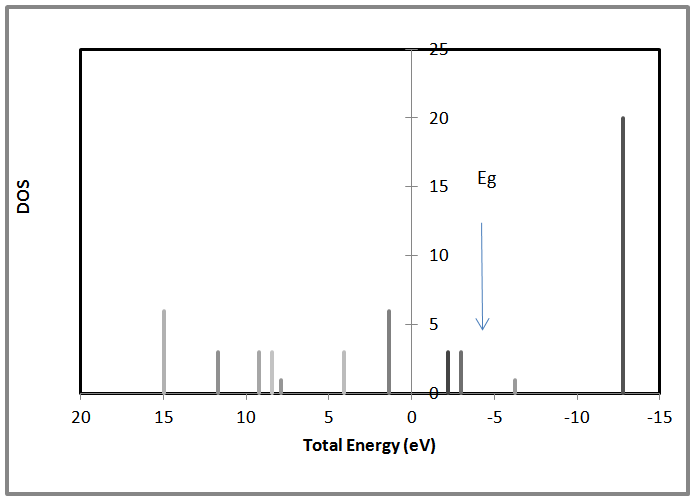 | Figure 8. Shows the density of states Vs the total energy for 8 atoms AlSb nanocrystal |
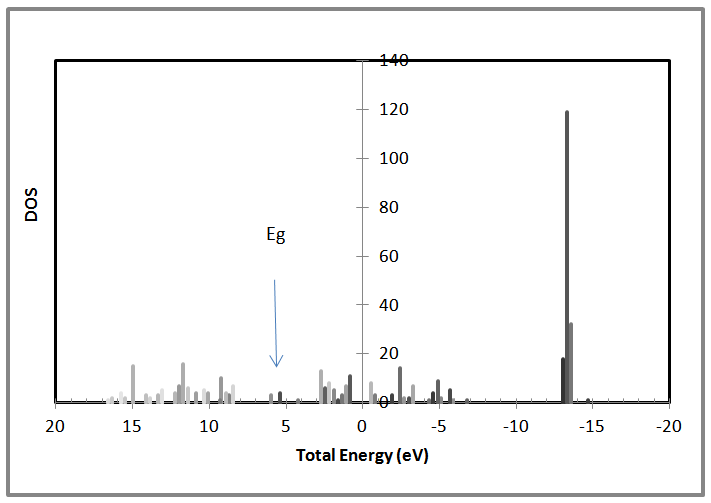 | Figure 9. Shows the density of states Vs the total energy for 64 atoms AlSb nanocrystal |
4. Conclusions
- A remarkable results found in this study is that the AlSb nanocrystals have a significant properties than bulk AlSb material. Ab-initio using the Gaussian 03 software stimulates some of important properties of nanocrystals rather than bulk materials. In the present work we can conclude that, the total energy, lattice constant and the energy gap are inversely proportional with the number of LUC core atoms while the density of states is proportional to the number of core atoms. The cohesive energy showed a fluctuated value with respect to increasing the number of core atoms. No significant dependency shown in this study between Ecoh. And the number of core atoms. Same behavior for both HOMO and LUMO with varying the number of core atoms.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML