Abdu S. G.1, Onimisi M. Y.2, Musa N.3
1Department of Physics, Kaduna State University, Kaduna, Nigeria
2Department of Physics, Nigerian Defence Academy, Kaduna, Nigeria
3Department of Applied Science, Kaduna Polytechnic, Kaduna, Nigeria
Correspondence to: Onimisi M. Y., Department of Physics, Nigerian Defence Academy, Kaduna, Nigeria.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The first and second ionization energies of the first ten elements of the periodic table were computed using the Hartree-Fock approximation code for small atomic systems developed by Koonin, S. E and Meredith, D. C. The results obtained compared fairly with the experimental values. The maximum and minimum values expected between helium at 31.4 eV and lithium at 3.4 eV for the first ionization energy and lithium at 86.7 eV and helium at 46.2 eV for the second ionization energy were observed. The spikes for the noble gases (helium and neon) were also observed for the first ionization energy. The computed values for the effective nuclear charge Z* had fairly, the same characteristics as the experimental results.
Keywords:
First ionization energy, Second ionization energy, Ground state energy, Hartree-Fock, Slater-determinant
Cite this paper: Abdu S. G., Onimisi M. Y., Musa N., Computation of the First and Second Ionization Energies of the First Ten Elements of the Periodic Table Using a Modified Hartree-Fock Approximation Code, American Journal of Condensed Matter Physics, Vol. 4 No. 3, 2014, pp. 51-56. doi: 10.5923/j.ajcmp.20140403.02.
1. Introduction
In quantum mechanics an atom can be viewed as a many-particle system [1], [2]. While the wave function for a single particle system is a function of only the coordinates of that particular particle and time, Ψ(r, t), a many-particle system will depend on the coordinates of all the particles.The Born-Oppenheimer Hamiltonian [3] for N electrons moving about a heavy nucleus can be written as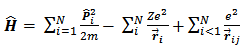 | (1) |
Here, (ri) is the location/position of electrons, m, -e, electron mass and charge respectively and  , the separation between electrons at i and j.The three sum of equation (1) embody [4]a. the electron kinetic energy (the first term)b. the electron-nucleus attraction (the second term)c. the electron-electron coulomb repulsion (the third term)For the accuracy of the Self Consistent Field, other approximations were neglected such as the spin-orbit interaction, hyperfine interaction, recoil motion of nucleus and relativity.By substituting
, the separation between electrons at i and j.The three sum of equation (1) embody [4]a. the electron kinetic energy (the first term)b. the electron-nucleus attraction (the second term)c. the electron-electron coulomb repulsion (the third term)For the accuracy of the Self Consistent Field, other approximations were neglected such as the spin-orbit interaction, hyperfine interaction, recoil motion of nucleus and relativity.By substituting 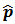 with the quantum mechanical operator
with the quantum mechanical operator 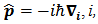 being the imaginary unit and
being the imaginary unit and 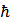 is the Planck’s constant divided by 2π, we get
is the Planck’s constant divided by 2π, we get | (2a) |
In the calculation of atomic structure, it is convenient to use Hartree’s atomic units (au) [4].The unit of mass = rest mass of the electron meThe unit of charge = the magnitude of the electronic charge, e.The unit of length = the first Bohr radius of the hydrogen atom 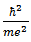 In these units, (2a) becomes
In these units, (2a) becomes | (2b) |
For one electron, (2b) can be solved exactly. The solution corresponding to bound states is 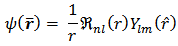 Electrons are Fermions which obey Pauli’s exclusion principle. This requires that the wave function of electrons should be anti-symmetric with respect to the interchange of coordinates x of any two electrons.
Electrons are Fermions which obey Pauli’s exclusion principle. This requires that the wave function of electrons should be anti-symmetric with respect to the interchange of coordinates x of any two electrons.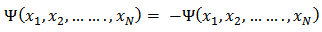 | (3) |
Slater determinants satisfy this anti-symmetric condition through appropriate linear combination of Hartree products, which are the non-interaction electron wave functions.It may be noted here that the Slater determinantal wave-function can be conveniently written as 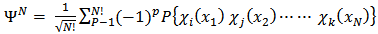 | (4) |
where the summation is over all possible N! number of permutations amongst the N completely identical electrons and p is the parity of the permutation P. [2]The many-body Hamiltonian for a system of N interacting electrons in the presence of nuclei fixed in some selected configuration can be written in the form | (5) |
where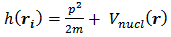 | (6) |
denotes for each electron the kinetic energy operator plus the potential energy due to the nuclei Eq. (4). In this case, 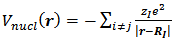 where
where 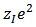 is the mutual attractive potential between the electron and the nucleus and
is the mutual attractive potential between the electron and the nucleus and  is their distance of separation.
is their distance of separation.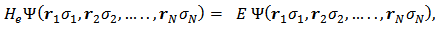 | (7) |
where  are the space and spin variables of the i-th electron. Although the Hamiltonian He does not include spin-dependent energy terms, the electron spin plays a fundamental role since the correct many-electron wavefunctions
are the space and spin variables of the i-th electron. Although the Hamiltonian He does not include spin-dependent energy terms, the electron spin plays a fundamental role since the correct many-electron wavefunctions 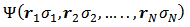 must be antisymmetric for interchange of the spatial and spin coordinates of any two electrons.The many-body electron Hamiltonian (5) contains two types of operators. One is the sum of one-particle operators of the form
must be antisymmetric for interchange of the spatial and spin coordinates of any two electrons.The many-body electron Hamiltonian (5) contains two types of operators. One is the sum of one-particle operators of the form | (8a) |
the other type is the sum of two-particle operators of the form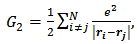 | (8b) |
which describes electron-electron interactions.Taking the expectation value of (8a) and (8b), we have: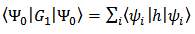 | (9a) |
 | (9b) |
and the expectation value of G2 on a given determinantal state thus becomes: | (10a) |
Which can be re-written as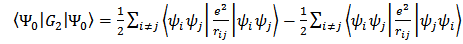 | (10b) |
The total ground state energy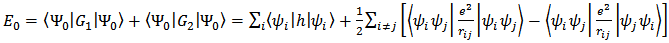 | (12) |
2. Materials and Methods
The materials used for this research were:• Fortran code developed by S. E. Koonin and D. C. Meredith in 1989 for the calculation of the ground-state energies of small atomic systems.• Origin 6.1 application software for graphical interpretation of the data generated from the Fortran code.• PC with Windows 7 operating system on which the application, Microsoft Developer Studio ® was mounted. It is used to run the Fortran code.The Hartree-Fock approximation code was compiled and debugged using Microsoft Developer Studio ®.The program is interactive. The DOS window that opens when in operation requests for the following:• The nuclear charge for the atomic system of interest• The number of electrons in the 1s, 2s and 2p states respectively• The radial step size measured in Angstrom unit• The outer radius of the lattice in Angstrom unit• The number of iterations• The choice of output for the resultο On the screenο Saved to a file with a filename of your choiceο Sent to a graphical output terminalThe code calculates • The total Kinetic energy, Ktot; inter-electron repulsive potential energy, Vee; Electron-nucleus attractive potential energy, Ven; Exchange potential energy, Vex; Total potential energy, Vtot; Total energy, Etot and the effective nuclear charge, Z*.The ground-state energy for the first ten elements of the periodic table was calculated using the electronic configuration of the respective elements
2.1. Computing First and Second Ionization Energies
To compute the first ionization energy of an element, we remove the outer electron from the lattice by deliberately reducing the number of electrons in the outer radius. For example, He has an electronic configuration of 1s2 2s0 2p0 at ground-state. We now remove one electron from the 1s2 orbital, giving us 1s1 2s0 2p0. The removal of the electrons from the elements is shown in Table 3.2. After entering the parameter required, we then ran the code for a number of iterations, all the while, looking at the result obtained. The iterations can be stopped immediately convergence was achieved. The total energy computed for each element was recorded and the ground state energy subtracted from it. The result obtained was recorded as the first ionization energy for the respective element.Using the same procedure, the second ionization energy was also calculated.The highly simplified algorithmic flowchart of the Hartree-Fock approximation is shown in Figure 1 below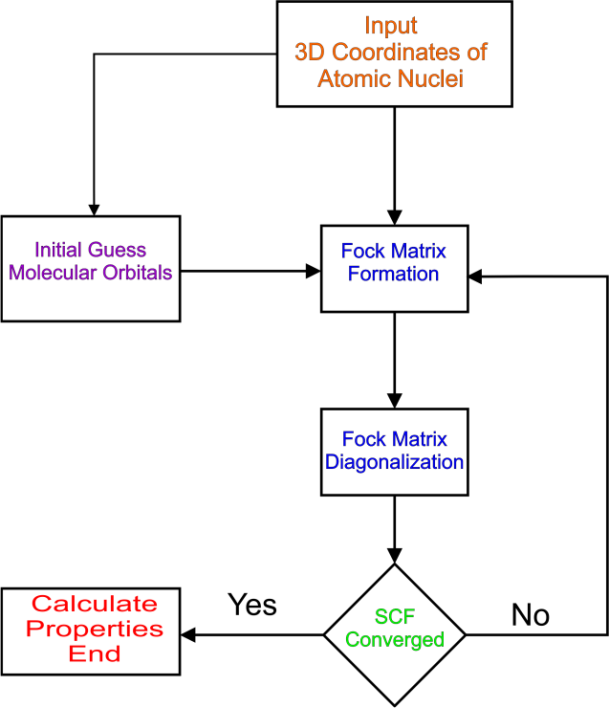 | Figure 1. Simplified algorithmic flowchart of the Hartree-Fock approximation |
3. Results and Discussion
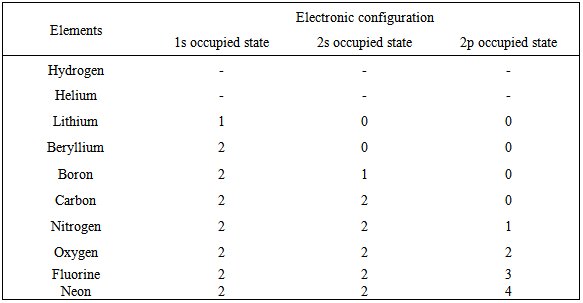
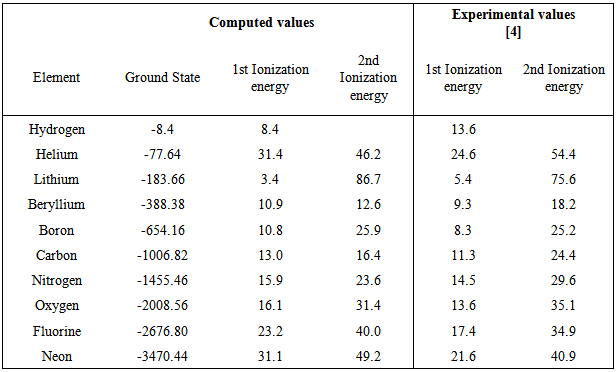
The following results were obtainedTable 1 gives the computed ground-state energy and the first and second ionization energies of the first ten elements. It also shows the experimental values for the first and second ionization energies of the first ten elements of the periodic table. From Table 1, the computed values for the ground-state energies of the ten elements are negative and decrease with increasing atomic number. This is because the energies bind the electrons to the nucleus. Commensurate amount of energy, called the binding energy will be required to remove the electrons bound to the respective nucleus from its position to the point where the kinetic energy is zero which implies that binding energy increases with increase in atomic number. [6]Table 1. Electronic configuration of first ten elements of the periodic table after removal of first electron
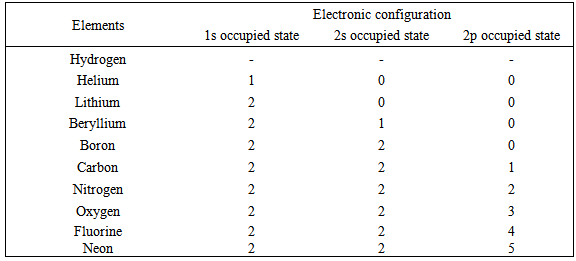 |
| |
|
Fig. 2, gives a graphical representation of the relationship between the ground-state energy and the elements.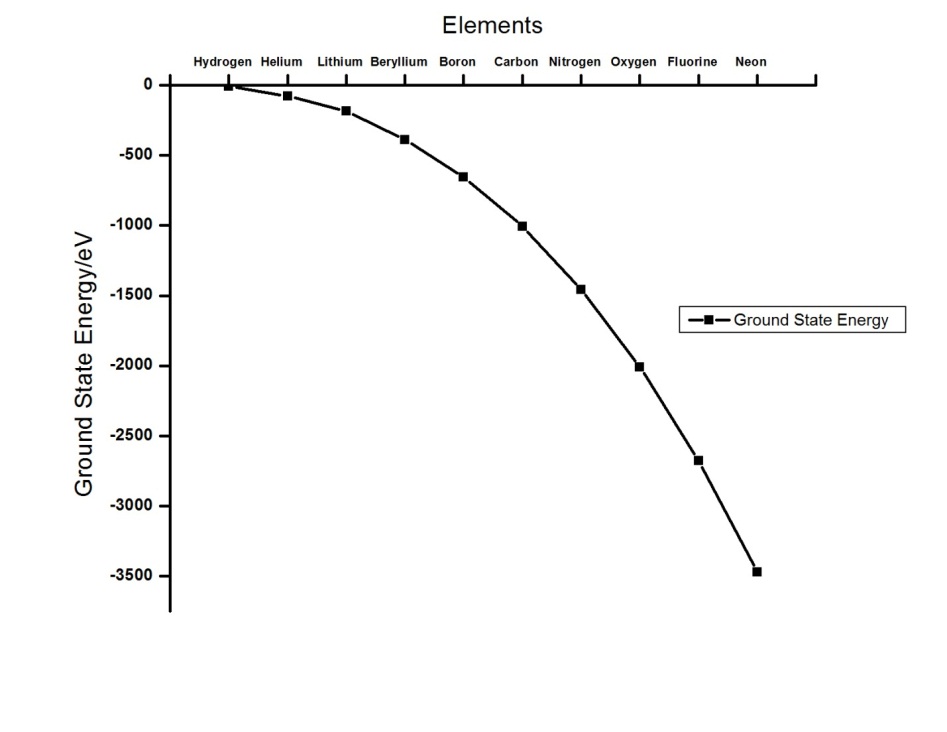 | Figure 2. Graph of Elements against ground-state energy |
From Figures 3-4, the comparison of our computed values and the experimental results for the first and second ionization energies against each element, shows a good similarity as the rise and dip at He and Li for the first ionization energy and Li and Be for the second ionization energies compare favourably.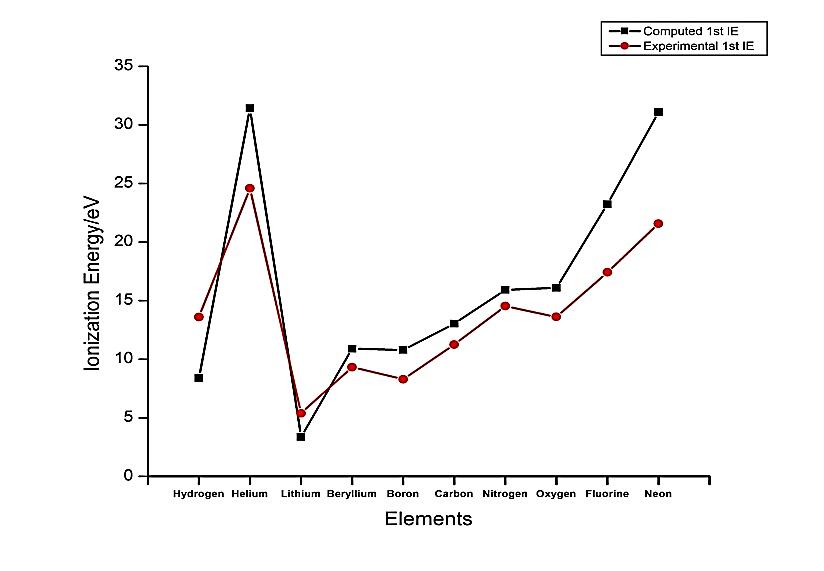 | Figure 3. Graph of Computed and calculated 1st I.E. against Elements |
 | Figure 4. Graph of Computed and Calculated 2nd I.E. against Elements |
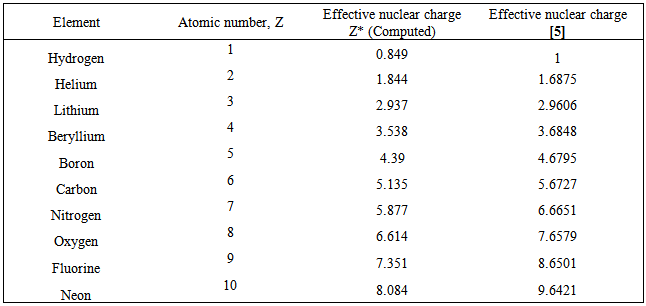
From Figure 3, we can see that the first ionization energy of helium (31.4 eV) is much greater than that of Lithium (3.4 eV). This is in agreement with [7]. The electrons provide some shielding for each other as mutual repulsion pushes them away from the nucleus. The outer electron of lithium occupies a new shell screened by two electrons and the ionization is much less than that of hydrogen or helium. This is in agreement with [8]From Table 1, the second ionization energies have higher values than the first ionization energies. This is because at the second ionization level, there are more protons than electrons holding the electrons down therefore more energy is required to pull out the second  [9]. The remarkable difference between the first and second ionization energies for lithium is due to the sudden breaking-in to an inner level, closer to the nucleus with less shielding [10].Table 2 shows the computed effective nuclear charge for the first ten elements of the periodic table. Z* shows a steady increase from Hydrogen to Neon. Going across the table, the effective nuclear charge increases because the electrons don not move farther away from the nucleus (stay in the same orbital). However, the charge of the nucleus increases as more protons are present. Because of shielding, the effective nuclear charge is somewhat less than the nuclear charge. [11]
[9]. The remarkable difference between the first and second ionization energies for lithium is due to the sudden breaking-in to an inner level, closer to the nucleus with less shielding [10].Table 2 shows the computed effective nuclear charge for the first ten elements of the periodic table. Z* shows a steady increase from Hydrogen to Neon. Going across the table, the effective nuclear charge increases because the electrons don not move farther away from the nucleus (stay in the same orbital). However, the charge of the nucleus increases as more protons are present. Because of shielding, the effective nuclear charge is somewhat less than the nuclear charge. [11]Table 2. Electronic configuration of first ten elements of the periodic table after removal of second electron
 |
| |
|
Table 3. Computed and calculated values of Ground-State, 1st and 2nd ionization energies
 |
| |
|
Table 4. Computed and Calculated Effective Nuclear charge of first ten elements of the periodic table
 |
| |
|
Figure 5 shows the graphical representation of computed effective nuclear charge Z1* against the experimental value for a hydrogenic atom. From the figure it can be seen that as the nucleus becomes more positive, Z* increases. | Figure 5. Graph of Computed and Calculated Effective nuclear charge vs. Elements |
The relationship between nuclear charge, Z and effective nuclear charge Z* isZ*=Z – Swhere S is the shielding factor [12].
4. Conclusions
The Hartree-Fock equation as a variational method was tested on the first ten elements of the periodic table using the Fortran code as developed by [4]. The characteristic zig-zig graphical pattern as we traversed the ten elements was observed. This is characteristic of all the elements as they have different properties that define them e.g. alkali earth metals, noble gases, etc.
References
| [1] | U. Rothlisberger and I. Tavernelli, 2011, “Electronic structure methods for molecular excited states.” http://www.tddft.org/TDDFT2008/lectures/IT3.pdf. Accessed on 3/10/2013. |
| [2] | P. C. Deshmukh, A. Banik, and D. Angom, Hartee-Fock self-consistent field method for many-electron system. nptel.iitm.ac.in/courses/115106057/STiAP_Unit_4_Hartree_Fock_L19_to_L23.pdf, 2011. Retrieved on 3/10/2013. |
| [3] | D. D. Fitts, Principles of quantum mechanics: as applied to chemistry and chemical physics. Cambridge University Press, Cambrigde IRP, 2002. |
| [4] | S. E. Koonin and D. C. Meredith, Computational physics (FORTRAN version), Westview Press, 1989. |
| [5] | dept.astro.lsa.umich.edu/~cowley/ionen.htm Accessed on 20/2/2014. |
| [6] | M. Gerken.classes.uleth.ca/200501/chem2810a/lecture_4.pdf extracted 14/4/2014 Chemistry lecture notes. |
| [7] | S. G. Abdu, 2010, Hartree-Fock solutions of the hydrogen, helium, lithium, beryllium and boron atoms. Nigerian Journal of Physics. 21(2). |
| [8] | F. Rioux, R. L. DeKock, 1998, J. Chem. Educ. 75, 537-539. |
| [9] | P. F. Lang, B. C. Smith, 2003, J. Chem. Educ. 8, 938-946. |
| [10] | wikianswers.com. |
| [11] | www.xtremepapers.com/revision/a-level/chemistry/atoms/properties/moreies.php Accessed on 20/2/2014. |
| [12] | www.chmdavidson.edu/ronutt/che115/zeff/zeff.htm Accessed on 8/3/2014. |

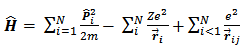
 , the separation between electrons at i and j.The three sum of equation (1) embody [4]a. the electron kinetic energy (the first term)b. the electron-nucleus attraction (the second term)c. the electron-electron coulomb repulsion (the third term)For the accuracy of the Self Consistent Field, other approximations were neglected such as the spin-orbit interaction, hyperfine interaction, recoil motion of nucleus and relativity.By substituting
, the separation between electrons at i and j.The three sum of equation (1) embody [4]a. the electron kinetic energy (the first term)b. the electron-nucleus attraction (the second term)c. the electron-electron coulomb repulsion (the third term)For the accuracy of the Self Consistent Field, other approximations were neglected such as the spin-orbit interaction, hyperfine interaction, recoil motion of nucleus and relativity.By substituting 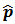 with the quantum mechanical operator
with the quantum mechanical operator 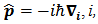 being the imaginary unit and
being the imaginary unit and 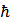 is the Planck’s constant divided by 2π, we get
is the Planck’s constant divided by 2π, we get
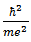 In these units, (2a) becomes
In these units, (2a) becomes
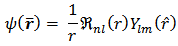 Electrons are Fermions which obey Pauli’s exclusion principle. This requires that the wave function of electrons should be anti-symmetric with respect to the interchange of coordinates x of any two electrons.
Electrons are Fermions which obey Pauli’s exclusion principle. This requires that the wave function of electrons should be anti-symmetric with respect to the interchange of coordinates x of any two electrons.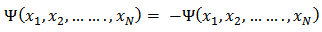
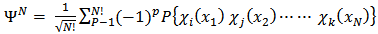

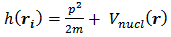
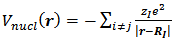 where
where 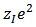 is the mutual attractive potential between the electron and the nucleus and
is the mutual attractive potential between the electron and the nucleus and  is their distance of separation.
is their distance of separation.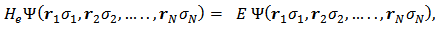
 are the space and spin variables of the i-th electron. Although the Hamiltonian He does not include spin-dependent energy terms, the electron spin plays a fundamental role since the correct many-electron wavefunctions
are the space and spin variables of the i-th electron. Although the Hamiltonian He does not include spin-dependent energy terms, the electron spin plays a fundamental role since the correct many-electron wavefunctions 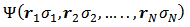 must be antisymmetric for interchange of the spatial and spin coordinates of any two electrons.The many-body electron Hamiltonian (5) contains two types of operators. One is the sum of one-particle operators of the form
must be antisymmetric for interchange of the spatial and spin coordinates of any two electrons.The many-body electron Hamiltonian (5) contains two types of operators. One is the sum of one-particle operators of the form
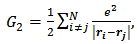
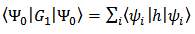


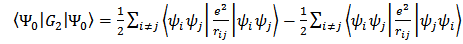
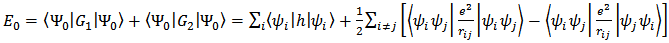




 [9]. The remarkable difference between the first and second ionization energies for lithium is due to the sudden breaking-in to an inner level, closer to the nucleus with less shielding [10].Table 2 shows the computed effective nuclear charge for the first ten elements of the periodic table. Z* shows a steady increase from Hydrogen to Neon. Going across the table, the effective nuclear charge increases because the electrons don not move farther away from the nucleus (stay in the same orbital). However, the charge of the nucleus increases as more protons are present. Because of shielding, the effective nuclear charge is somewhat less than the nuclear charge. [11]
[9]. The remarkable difference between the first and second ionization energies for lithium is due to the sudden breaking-in to an inner level, closer to the nucleus with less shielding [10].Table 2 shows the computed effective nuclear charge for the first ten elements of the periodic table. Z* shows a steady increase from Hydrogen to Neon. Going across the table, the effective nuclear charge increases because the electrons don not move farther away from the nucleus (stay in the same orbital). However, the charge of the nucleus increases as more protons are present. Because of shielding, the effective nuclear charge is somewhat less than the nuclear charge. [11]
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML


