1. Introduction

Molecular potentials, [1,2] energy gap, [3] ionicity, polarity, [4] phase transition, [5] etc. are very important characteristics determined by charge transfer. [6] On the other hand, many applications such as optoelectronics, [7] shielding, [8] resistant coating surface [9] and others depend on properties like bulk modulus, [10] sound velocity [11 and plasma frequency [12] which can be regarded as a result of charge distribution. [13] However; it is well known that materials size can effectively affect their properties and applications, [14,15] On account of such remarkable phenomenon many studies have been motivated to investigate materials in dimensions up to unit cell. [16-20]

Researchers consider III-V semiconductors as the most interesting type of materials due to their impressive characteristics and behavior. [21] For these reasons scientists have studied these materials using both first principle calculations for their accuracy, [22] and density functional theory (DFT) for its successful handling of many properties, especially the electronic structure. [14,23] However, knowing that Kohn-Sham DFT is insufficient method for its deficiencies concerning the gap issue, [24] and the long range interactions approximations, [25] the generalized gradient approximation (GGA) has been applied here, since it has recently been extensively used and proved to be an effective method for properties calculation [26-28 such as total energy, binding energy, molecular dimensions. [29]

Our aims are to find out the effect of compression on intermolecular charge transfer for small group of semiconductors and to check the effectiveness of the way chosen for calculation. Depending on the credibility of outputs, a comprehensive study would be presented. In order to execute this task, we have implemented the restricted Hartree–Fock (RHF) method, a successful proved tool, [30,31] in companying with the DFT within the Perdew, Burke, and Ernzerhof (PBE-GGA) framework [32-34] using GAUSSIAN 03 program. [35]

2. Method

The self-consistent Hartree–Fock method is used in the present work to obtain the electronic structure. Correlation corrections can be neglected in some closed-shell calculations (which is the case of the present work) using Koopmans theorem [36] owing to the cancellation of correlation corrections with relaxation. STO-3G basis states are used as the simplest basis to reach higher number of atoms. [30,31,37,38]

Large unit cell (LUC) method coupled with ab-initio Hartree-Fock self-consistent electronic structure calculations are used in the present work. This method was formulated and used previously to investigate the electronic structure of several kinds of bulk materials including diamond, [30,37-39] and nanocrystals like silicon [31] with smaller number of atoms. The LUC method is one kind of supercell methods with the (k=0) restriction, when is one point in the wave vector space. In this method, and instead of adding more k points, the single central cell is expanded to contain more atoms, which are now called core atoms in the present work. We found it very suitable for describing the core of a nanocrystal since it still has the outer dangling bonds that are saturated by surface atoms. The method does not expand to contain the whole space; instead it contains only the real number of atoms in a nanocrystals core that has nearly the exact diamond structure. [40]

3. Results and Discussion

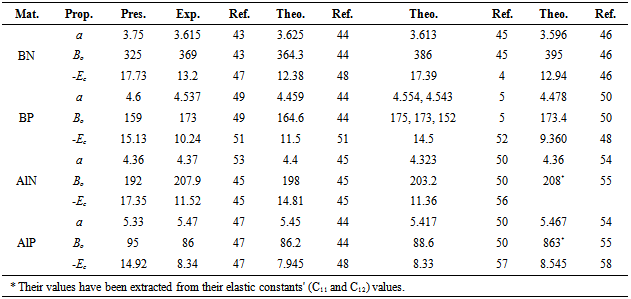
Our calculated properties for III-V compounds are illustrated in Table 1, these results are in reasonable agreement with other experimental and theoretical calculations. On one hand, lattice constants of BN and BP are overestimated, but this result is considered as a normal consequence of the current method. [41] Nevertheless, it can also be considered as a deficiency for this research. On the other hand, it is well known that these clusters are polar, as shown in Figure 1, and it is obvious that under compression both molecular electrostatic potential difference, calculated by Molekel Program, [42] and volume decrease as shown in Figure 2. While the charge concentration in the atom basins increases as in Figure 3. In the meanwhile, it is observed that the charges transfer from cations to anions (C⁺δ→A^-δ) except for B⁺δP^-δ (P→B) as shown in Figures 4 and 5.

It should be kept in mind that our charge calculations depend on Mullikan technique (MT). This model does not describe the charge density in details, but gives equal shears of charges for heteropolar semiconductor atoms (+Q_C = -Q_A). [59].

The main results show that the compression increases electron concentration due to the volume decreasing, as shown in Figures 2 and 3. [60] The resulted charge distribution, [61] which depends on the electronegativity (χ), moderates the antisymmetric potentials of atoms [62] and so it increases ionicity. On the other hand, as a results of the absence of the p-shell in the valence of B atom, [61] the covalent behavior appears clearly. [60]

Leaning on atoms in molecules theory (AIM) we can regard our clusters as a group of quantum atoms, especially by considering MT. [63] AIM theory consider atoms as individual basins, in order that charges can transfer from one reservoir to another, depending on the atoms’ χ. The more the electronegativity, the more the attraction is.

On the other hand, the atom's compressibility determines the resistance to deformation, and bulk modulus is a measure of covalency. However; high bulk modulus means high covalency and low ionicity in both zinc blende [64] and wurtzite structures [65] which can be attributed to the decreasing of the effective charge. [66] But charge flow is a reflex of the ionicity. [67] So it can be resemble as a ionic flavor for the whole covalent system.

It is well known that the molecular electrostatic potential (MEP), Figure 1, around N in BN and AlN, B in BP, and P in AlP leads to more flow of charges from cation to anion. [59] Less distance due to compression means less screening of the core upon the valence electrons, and so more attraction on them. [68] Then atoms with high χ, N is the highest, [69] will pull electrons effectively. While the BP’s anomalous flow can be attributed to high χ of B and the p-pseudopotential absence, [5] as shown in Figures 4 and 5. Our results are in consistent with previous studies such Sánchez et al. [5] for BP crystals, they illustrated that the anomalous behavior of this kind can be attributed to a transition state, in which the charges accumulate within the bond space not around the atoms. [5] Our calculations for charge distributions are in consistent with Wentzcovitch et al. results for BN and BP, [51] Sanjurjo et al. for their semiconductors, [66 and Saib et al for AlN. [70]

Table 1. The lattice constant in (A), bulk modulus in (GPa), and cohesive energy in (eV/pair) of BN, BP, AlN, and AlP

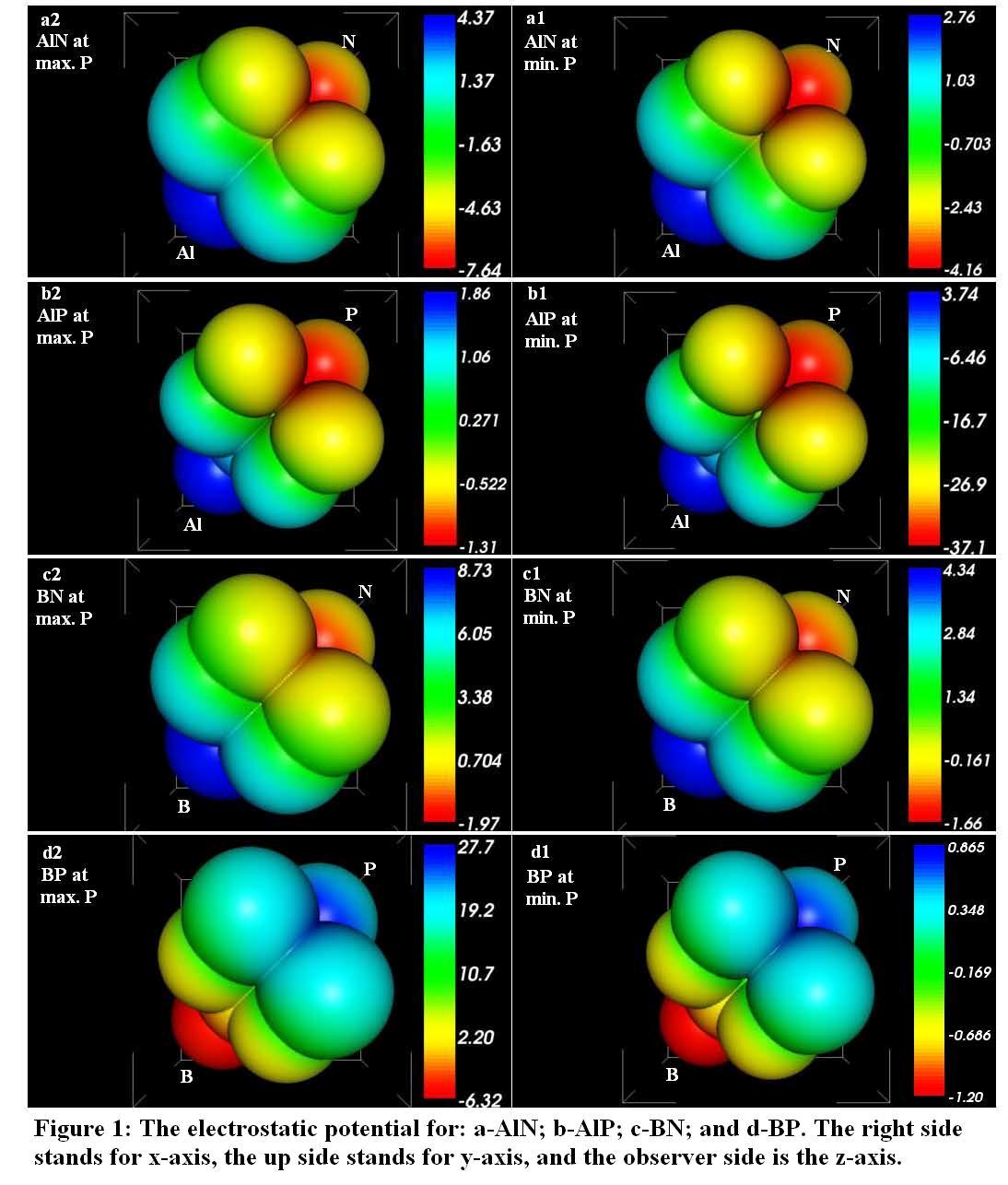Figure 1. The electrostatic potential for:a-AIN; b-AIP;c-BN; and d-BP. The right side stands for x-axis, the up side stands for y-axis, and the observer side is the z-axis

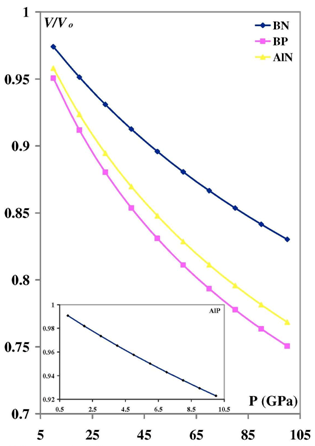Figure 2. the pressure dependence of volume

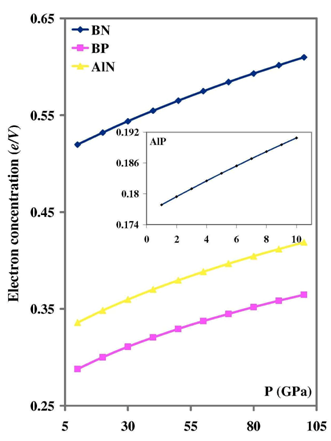Figure 3. the pressure dependence of electron concentration

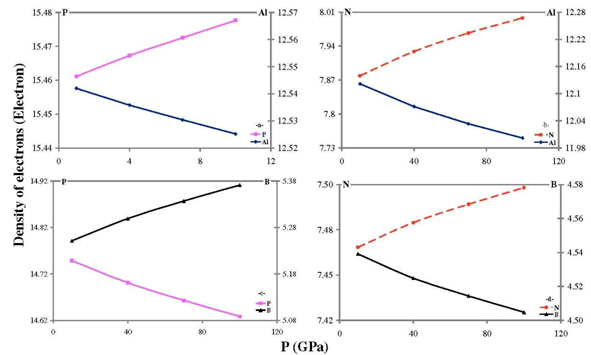Figure 4. The effect of compression on the number of electrons condensed to each atom for:(a) AIP; (b) AIN; (c) BP; and (d) BN

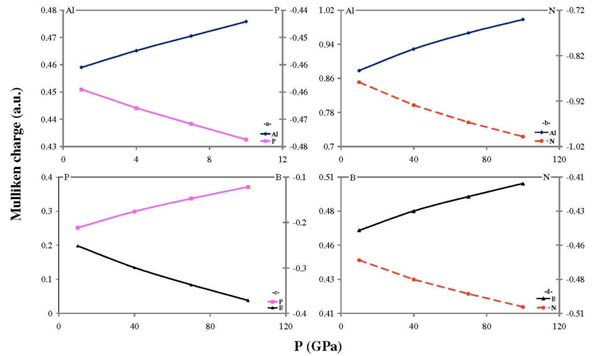Figure 5. The effect of compression on Mulliken atomic charge for:(a) AIP; (b) AIN; (c) BP; and (d) BN

4. Conclusions

It is obvious that within the strongly presence of covalency due to compression, there are small trends of ionic transfer. This transfer can be regarded as the flavor of each compound because it shows their significant properties. Generally, all materials subject to the same rule which is; the more the electronegativity, the more attraction. So BP behaves in normal way.