Famous Akpojotor1, Ejiroghene Akpojotor2, Lawrence Atuma3
1Physics Department, University of Benin, Benin City, Nigeria
2Physics Department, Delta State University, Abraka, Nigeria
3Physics Department, Delta State Polytechnic, Oghara, Nigeria
Correspondence to: Famous Akpojotor, Physics Department, University of Benin, Benin City, Nigeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
We calculated the exact self energy and the exact Green’s function for the Bethe lattice in the hopping model using the Dyson’s equation and from the fourth order of perturbation theory. The self energy is found from processes where an electron hops to its neighbors and includes terms where the particle hops twice to a next nearest neighbor (NNN) and then hops back.
Keywords:
Bathe lattice, Green function, Exact Solution, Self energy
Cite this paper: Famous Akpojotor, Ejiroghene Akpojotor, Lawrence Atuma, Exact Green’s Function for the Bethe Lattice in the Hopping Model, American Journal of Condensed Matter Physics, Vol. 4 No. 1, 2014, pp. 20-24. doi: 10.5923/j.ajcmp.20140401.03.
1. Introduction
The Bethe lattice has received huge interest in statistical mechanics because of its peculiar structure. Several interesting physical problems involving interactions are exactly solvable when defined on the Bethe lattice[1 – 5]. This has made it the candidate lattice to investigate various kinds of interactions and models. The Bethe lattice is an infinite tree graph, where any two points are connected by a single path and each vertex has the same number of branches[6]. Like most many body problems, it is not straightforward to obtain simple analytical approaches to explore the physics emanating from the Bathe lattice system. Within the harmonic approximation, the Green’s function represents perhaps the simplest type of many body problems. The Green’s function approach provides a unified systematic method for calculating various quantities of physical interest. It gives the ground state energy of a system and provides information on the excitation energies of the system[7]. It is applied to difficult problem of lattice dynamics of a harmonic crystal. Green’s function makes it possible to evaluate measurable thermodynamic and transport properties by studying the response of a simple perturbation[8, 9]. The local Green function for a quantum- mechanical particle with hopping between its nearest neighbor (NN) and next nearest neighbor (NNN) on the Bethe lattice has been calculated[10], where the on-site energies may alternate on sub-lattices. For infinite connectivity the renormalized perturbation expansion was carried out by counting all non-self intersecting paths, leading to an implicit equation for the local Green function. By integrating out branches of the Bethe lattice, the same equation is obtained from a path integral approach for the partition function. In this study, the electron Green’s function will be used to calculate the exact Green’s function and self energy for the Bethe lattice in the hopping model. Though it is not one of the goals of our study here, it is pertinent to point out that the self energy can be used to obtain the vertex function which contains all the information on the kinetic and interaction behaviour of the particles in the system. Interestingly the vertex function can be decoupled into the charge vertex function and spin vertex function, thereby enabling the studying of either non-spin ordering systems or spin ordering system independently.
2. The Electron Green’s Function
The electron Green’s function is defined as[6] 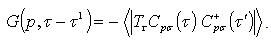 | (1) |
Re-expressing Eqn. (1) in the Heisenberg representation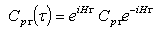 | (2) |
so that  is independent of time τ, we obtain
is independent of time τ, we obtain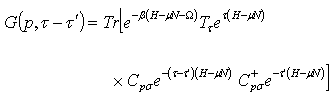 | (3) |
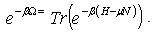 | (4) |
The bracket 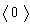 on an operator 0 means we should take the thermodynamic average which is a trace over the complete set of states. The Hamiltonian is replaced by H-μN where μ is the chemical potential and N is the particle number operator. This definition of the Green’s function applies to a many particle system. It can also be used very successfully for one particle in an empty band. Here it is consider for an electron.
on an operator 0 means we should take the thermodynamic average which is a trace over the complete set of states. The Hamiltonian is replaced by H-μN where μ is the chemical potential and N is the particle number operator. This definition of the Green’s function applies to a many particle system. It can also be used very successfully for one particle in an empty band. Here it is consider for an electron.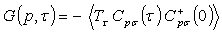 | (5) |
The factor 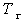 is a
is a 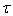 -ordering operator which arranges operators with earlier τ to the right (closest to -β). It serves the same function as the time ordering operator in the zero temperature Green’s functions. The subscript τ is affixed to T to distinguish this operator from the temperature. The thermodynamic potential Ω in exp(-β Ω) is the usual normalization factor for a thermodynamic average.
-ordering operator which arranges operators with earlier τ to the right (closest to -β). It serves the same function as the time ordering operator in the zero temperature Green’s functions. The subscript τ is affixed to T to distinguish this operator from the temperature. The thermodynamic potential Ω in exp(-β Ω) is the usual normalization factor for a thermodynamic average.
3. Exact Green’s Function for the Bethe Lattice
The Green’s function for the Bethe lattice will be calculated from the Hamiltonian with the NN hopping term, as given by[9]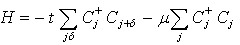 | (6) |
where t is the kinetic hopping term that describes the itinerancy tendency of the electron and the other parameters retain their usual meanings[11, 12].The summation over δ runs over the z neighbors. Spins plays no role in this calculation and will be omitted. The last term contains the chemical potential μ. The standard model of particle motion has hopping between nearest neighbor sites using a tight-binding model.Defining the electron Green’s function of Eqn. (1) as 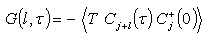 | (7) |
where all the parameters retain their earlier definitions. The expectation value in Eqn. (7) can be transformed into trace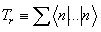 | (8) |
where the symbol Tr denotes trace.Taking into account Eq. (8) and the Heisenberg representation,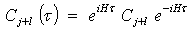 | (9) |
Eq.(7) becomes 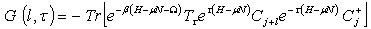 | (10) |
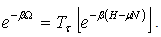 | (11) |
For compactness, we introduce 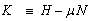 .Then considering
.Then considering 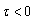 , we obtain
, we obtain 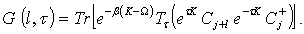 | (12) |
Using the theorem that trace is unchanged by a cyclic variation of the operators,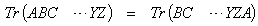 | (13) |
it can be shown that 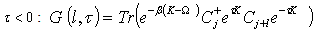 | (14) |
By using the cyclic property of the trace several times, Eqn. (14) can be re-arrange into 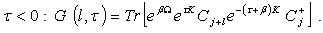 | (15) |
The factor exp (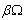 ) is not cycled since it is not an operator. These terms can be regrouped by adding exp
) is not cycled since it is not an operator. These terms can be regrouped by adding exp 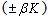 to the first terms to give
to the first terms to give 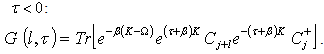 | (16) |
We deploy the fermion Green’s function property,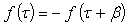 | (17) |
when 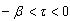 , to obtain the term on the right side of Eqn. (17) as
, to obtain the term on the right side of Eqn. (17) as 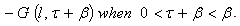 These steps show that
These steps show that 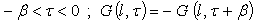 | (18) |
Expanding the Green’s function in the Fourier series as 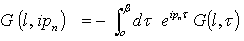 | (19) |
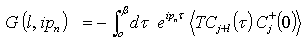 | (20) |
Eqn. (19) serves as the definition G(l, ipn), where ipn is always an odd multiple of π/β for fermions. The non-interacting Green’s function is obtained from Eqn. (12) by the use of the Hamiltonian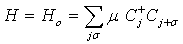 | (21) |
The 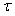 dependence of the Green’s function is
dependence of the Green’s function is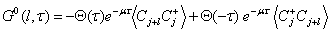 | (22) |
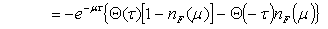 | (23) |
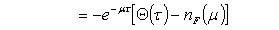 | (24) |
where 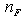 (µ) is the expectation of the number operator
(µ) is the expectation of the number operator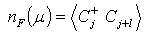 | (25) |
which gives 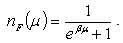 | (26) |
Obtaining the Green’s function of frequency for l = 0 | (27) |
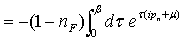 | (28) |
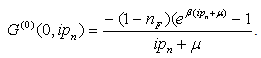 | (29) |
The second term in the numerator may be simplified upon recalling that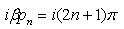 | (30) |
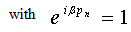 | (31) |
which gives 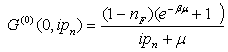 | (32) |
From Eqn (26),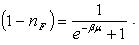 | (33) |
Therefore, 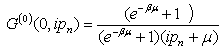 | (34) |
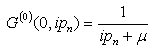 | (35) |
Equation (35) is the non-interacting Green’s function for l = 0Consider the Green’s function of energy defined by taking the usual Fourier transform with respect to the time variable equation, we obtain 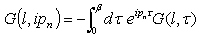 .The Fourier transform in time is applied to each term in the S-matrix summation
.The Fourier transform in time is applied to each term in the S-matrix summation 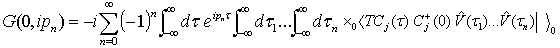 | (36) |
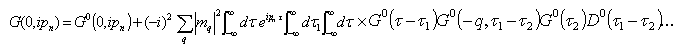 | (37) |
The Green’s function integral is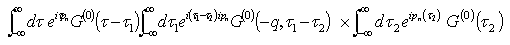 | (38) |
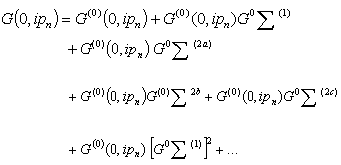 | (39) |
Summing the terms in the series Eqn. (39) yield self energy diagrams which may be collected into the Dyson equation.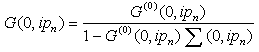 | (40) |
where the total self energy 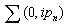 is the summation of all the different self energy contribution
is the summation of all the different self energy contribution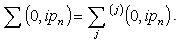 | (41) |
The Dyson’s equation is really a theorem which states that one may sum the series of energy terms which develops in higher order and the form of Eqn. (40) is obtained with each distinct contribution to ∑ occurring just once[9].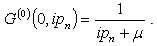 The self energy
The self energy 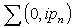 is found from processes where an electron hops to its neighbors and then hops back. Each hop has a matrix element t. The total number of hops in each self-energy is an even number such as 2n. For 2n hops, which return the particle to the original site, the lowest order self-energy (n = 1) is from the process where a particle hops to the neighbors and then hops back to the original site. There are z neighbors and the intermediate Green’s function at the neighboring site must be G(0)(0,ipn). The self-energy from double hops is
is found from processes where an electron hops to its neighbors and then hops back. Each hop has a matrix element t. The total number of hops in each self-energy is an even number such as 2n. For 2n hops, which return the particle to the original site, the lowest order self-energy (n = 1) is from the process where a particle hops to the neighbors and then hops back to the original site. There are z neighbors and the intermediate Green’s function at the neighboring site must be G(0)(0,ipn). The self-energy from double hops is 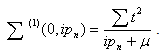 | (42) |
The next in the self energy comes from the fourth order of perturbation theory and includes terms where the electron hops twice to a NNN and then hops back. The first hop has a bandwidth of z–1 since the hop back to the starting point has already been included and the resulting self energy will be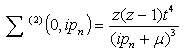 | (43) |
Therefore, including both terms gives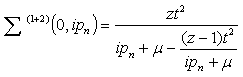 | (44) |
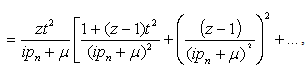 | (45) |
where the terms in the bracket are with higher dimension in the perturbation expansion. The terms in the series in the brackets describes processes where after hopping to the first neighbor, the electron hops to and from its neighbors multiple times before hopping back to the original site once. When it hops away from the original site the second time, it counts as another self energy function.The factor multiplying zt2 in Eqn. (44), 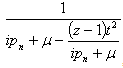 ,has the appearance of a Green’s function. It has the Green’s function for the electron as it hops around. The same Green’s function should be in its own denominator. This process leads to a continued fraction
,has the appearance of a Green’s function. It has the Green’s function for the electron as it hops around. The same Green’s function should be in its own denominator. This process leads to a continued fraction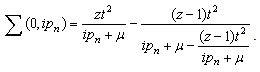 | (46) |
Every denominator is the same. Further terms in the continued fraction describe processes where the particle hops further away in the lattice. The continued fraction contains all forward hops to all sites. This expression is the self energy.Defining the self energy in the denominator of Eqn. (44) as ∑D, then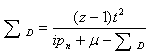 | (47) |
The continued fraction yields a quadratic equation which is solved easily: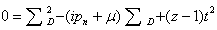 | (48) |
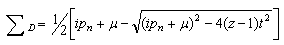 | (49) |
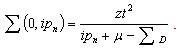 | (50) |
Substituting ∑D of Eqn. (49) into Eqn.(50) gives 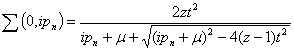 | (51) |
which is the exact self energy. Thus the exact Green’s function for the Bethe lattice in the hopping model becomes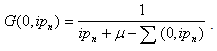 | (52) |
4. Conclusions
We have developed an exact Green’s function and self energy for the Bethe lattice in the hopping model. The physics of most strongly correlelated systems are generally believed to be influenced by the hopping of the electron often referred to as the electron itinerancy. For systems with broad energy band, they have large kinetic energy so that the electrons are highly itinerant thereby spending less time at the atomic sites. Such delocalized electrons can be described by assuming an independent particle picture[12]. For systems with narrow energy band, they have small kinetic energy so that the electrons spend more time at the atomic sites. Such localized electrons are correlated and therefore need to be described as quasiparticles. Now for system that are partially itinerant and partially localized such as in correlated systems, most model Hamiltonians formulated to explore them usually have the electron itinerancy represented to competes with the correlated interaction[11 – 14]. Therefore it is expected that our formulation will be very useful in investigating the effects of the electron itinerancy in these models using the Bathe lattice. Further, we have considered the hopping restricted to the NNN here. It will also be worthwhile to investigate the effects which hopping beyond NNN has on the physics of interacting many-body and disordered systems on the Bethe lattice.
References
| [1] | da Silva C. R. and Coutinho S. (1986) Ising model on the Bethe lattice with competing interactions up to the third-nearest-neighbor generation. Phys. Rev. B34, 7975-7985. |
| [2] | Mancini F.P. (2009) Magnetic Properties of a Strongly Correlated System on the Bethe Lattice. J. of Phys. Studies 13, 4702-(1-8). |
| [3] | Jurcisinova E. and Jurcisin M. (2012) Critical Temperatures of the Ising Model on the Bethe Lattice for Arbitrary Values of Spin. Int. J. of Modern Phys. 26, 1250003. |
| [4] | Liang T. and Min L. (2012) Relaxation of Evolutionary Dynamics on the Bethe Lattice. Chinese Phys. Lett. 29, 038701. |
| [5] | Akpojotor F.A., Babalola M.I. and Idiodi J.O.A. (2012) The Ising Model on the Bethe Lattice. J. NAMP 22, 43-48. |
| [6] | Eckstein M., Kollar M., Byczuk K. and Vollhardt D. (2005) Hopping on the Bethe Lattice; Exact results for Densities of States and Dynamical Mean-Field Theory. Phys. Rev. B71, 235119-1 – 235119-13. |
| [7] | Baxter R.J. (1982) Exactly solved models in Statistical Mechanics. Academic Press, London. |
| [8] | Doniah S. and Sondheimer E.H. (1974) Green’s Functions for Solid State Physicist. Academic Press, London 1974. |
| [9] | Mahan G.D. (2000) Many Particle Physics. 3rd edition. Kluwer Academic/Plenum Publishers, New York. Mahan G.D. (2001) Energy bands of the Bethe lattice. Phys. Rev. B63, 155110-1 – 155110-5. |
| [10] | Kollar M., Eckstein M., Byczuk K., Blumer N., van Dongen P., Redke de cube M.H., Metzner W., Tanaskovie D., Dobrosavljevic V., Kotliar G. and Vollhardt D. (2005) Green Functions for Nearest and Next Nearest Neighbor Hopping on the Bethe Lattice. Ann. Phys. 14, 642-657. |
| [11] | Akpojotor G.E. (2008), “The statistical equivalents of the t-U and t-t-U models” in Lectures on the Physics of Strongly Correlated Systems XII (edited by A. Avella and F. Mancini), AIP Con. Proc. 1014, 251 -259. |
| [12] | Ogata M and Fukuyama H (2008) The t – J model for the oxide high-Tc superconductors, Rep. Prog. Phys. 71 036501. |
| [13] | Akpojotor G.E and Akpojotor F. (2009) A highly simplified correlated variational study of the singlet-triplet transition in quantum dots embedded in kagome lattice. Proceedings of the 2008 Joint NSBP and NSHP Conference, AIP Con. Proc. 1040, 54-59. |
| [14] | Tsvelik A. M (Editor) (2001) New theoretical approaches to strongly correlated systems, kluwar academic publishers. |

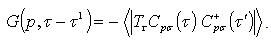
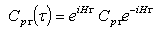
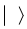 is independent of time τ, we obtain
is independent of time τ, we obtain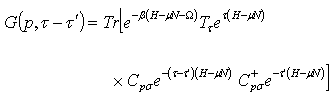
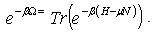
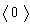 on an operator 0 means we should take the thermodynamic average which is a trace over the complete set of states. The Hamiltonian is replaced by H-μN where μ is the chemical potential and N is the particle number operator. This definition of the Green’s function applies to a many particle system. It can also be used very successfully for one particle in an empty band. Here it is consider for an electron.
on an operator 0 means we should take the thermodynamic average which is a trace over the complete set of states. The Hamiltonian is replaced by H-μN where μ is the chemical potential and N is the particle number operator. This definition of the Green’s function applies to a many particle system. It can also be used very successfully for one particle in an empty band. Here it is consider for an electron.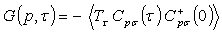
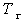 is a
is a 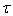 -ordering operator which arranges operators with earlier τ to the right (closest to -β). It serves the same function as the time ordering operator in the zero temperature Green’s functions. The subscript τ is affixed to T to distinguish this operator from the temperature. The thermodynamic potential Ω in exp(-β Ω) is the usual normalization factor for a thermodynamic average.
-ordering operator which arranges operators with earlier τ to the right (closest to -β). It serves the same function as the time ordering operator in the zero temperature Green’s functions. The subscript τ is affixed to T to distinguish this operator from the temperature. The thermodynamic potential Ω in exp(-β Ω) is the usual normalization factor for a thermodynamic average.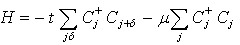
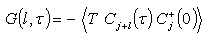
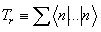
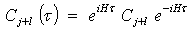
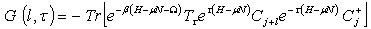
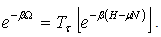
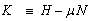 .Then considering
.Then considering 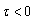 , we obtain
, we obtain 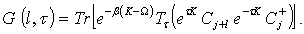
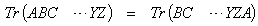
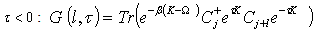
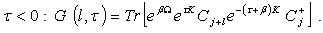
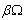 ) is not cycled since it is not an operator. These terms can be regrouped by adding exp
) is not cycled since it is not an operator. These terms can be regrouped by adding exp 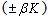 to the first terms to give
to the first terms to give 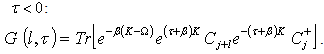
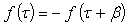
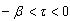 , to obtain the term on the right side of Eqn. (17) as
, to obtain the term on the right side of Eqn. (17) as 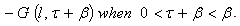 These steps show that
These steps show that 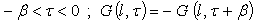
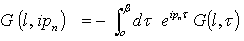
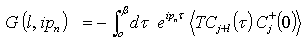
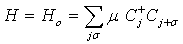
 dependence of the Green’s function is
dependence of the Green’s function is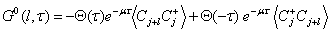
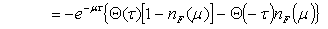
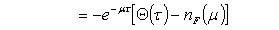
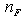 (µ) is the expectation of the number operator
(µ) is the expectation of the number operator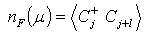
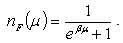

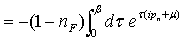
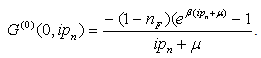
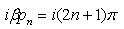
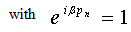
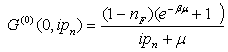
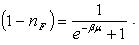
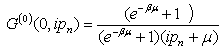
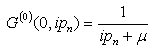
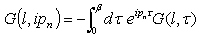 .The Fourier transform in time is applied to each term in the S-matrix summation
.The Fourier transform in time is applied to each term in the S-matrix summation 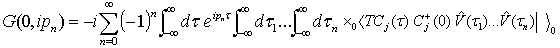
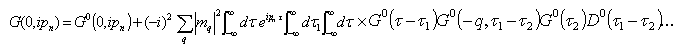
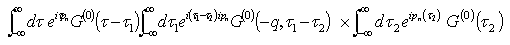
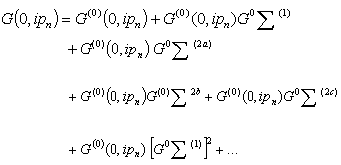
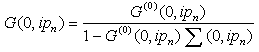
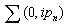 is the summation of all the different self energy contribution
is the summation of all the different self energy contribution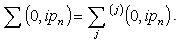
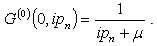 The self energy
The self energy 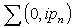 is found from processes where an electron hops to its neighbors and then hops back. Each hop has a matrix element t. The total number of hops in each self-energy is an even number such as 2n. For 2n hops, which return the particle to the original site, the lowest order self-energy (n = 1) is from the process where a particle hops to the neighbors and then hops back to the original site. There are z neighbors and the intermediate Green’s function at the neighboring site must be G(0)(0,ipn). The self-energy from double hops is
is found from processes where an electron hops to its neighbors and then hops back. Each hop has a matrix element t. The total number of hops in each self-energy is an even number such as 2n. For 2n hops, which return the particle to the original site, the lowest order self-energy (n = 1) is from the process where a particle hops to the neighbors and then hops back to the original site. There are z neighbors and the intermediate Green’s function at the neighboring site must be G(0)(0,ipn). The self-energy from double hops is 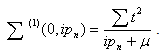
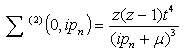
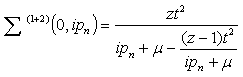
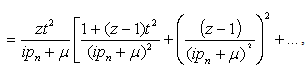
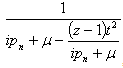 ,has the appearance of a Green’s function. It has the Green’s function for the electron as it hops around. The same Green’s function should be in its own denominator. This process leads to a continued fraction
,has the appearance of a Green’s function. It has the Green’s function for the electron as it hops around. The same Green’s function should be in its own denominator. This process leads to a continued fraction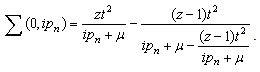
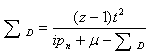
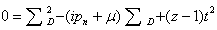
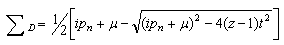
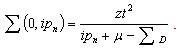
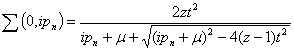
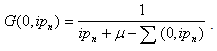
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML