-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Condensed Matter Physics
p-ISSN: 2163-1115 e-ISSN: 2163-1123
2013; 3(5): 133-136
doi:10.5923/j.ajcmp.20130305.03
Incommensurate Phase in Ferroelectrics: The Urbach Energy Remains Unchanged
Ihor Studenyak1, Alexander Slivka1, Mladen Kranjcec2
1Physics Department, Uzhhorod National University, Uzhhorod, 88000, Ukraine
2Geotechnical Department, University of Zagreb, Varazdin, 42000, Croatia
Correspondence to: Ihor Studenyak, Physics Department, Uzhhorod National University, Uzhhorod, 88000, Ukraine.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Temperature invariance of the Urbach energy and parallel red shift of optical absorption edge in the incommensurate phase of Sn2Р2Se6 ferroelectric is analyzed. The observed effect is explained by the presence of dynamic structural disordering of the crystal lattice caused by a wave of structure modulation which is formed by the shift of tin atoms.
Keywords: Phase Transition, Incommensurate Phase, Absorption Edge
Cite this paper: Ihor Studenyak, Alexander Slivka, Mladen Kranjcec, Incommensurate Phase in Ferroelectrics: The Urbach Energy Remains Unchanged, American Journal of Condensed Matter Physics, Vol. 3 No. 5, 2013, pp. 133-136. doi: 10.5923/j.ajcmp.20130305.03.
1. Introduction
- It is well known that for a great number of solids absorption near the optical absorption edge increases exponentially and the spectral dependences of the absorption coefficient at different temperatures are described by the Urbach rule[1]. Since the discovery of this universal rule, it was set for a number of ferroics: ferroelectrics (e.g.[2-6]), ferrielectrics (e.g.[7,8]), antiferroelectrics (e.g.[9]), and ferroelastics (e.g.[10,11]). However, despite its versatility, in many cases deviations from this rule are observed. Some of these materials are ferroelectrics with incommensurate phase. The aim of this paper is an attempt to explain the non-Urbach behaviour of the optical absorption edge in incommensurate phases of some ferroelectrics from the standpoint of disordering processes and the presence of the dynamic component of structural disordering caused by the structure modulation. As an example, we have chosen Sn2Р2Se6 crystal which belongs to proper uniaxial ferroelectrics, in which at low temperatures two phase transitions exist, one of which is a phase transition from the paraelectric phase to the incommensurate phase at Тi =221 K, the other is the phase transition from the incommensurate phase to the ferroelectric phase at Тс=193 K[4, 5, 12].
2. Theory
- In 1953, F. Urbach was the first to observe experimentally the exponential behaviour of absorption edge spectra in AgBr crystal, which formed a characteristic “bundle” at the temperature increase[1]:
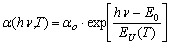 | (1) |
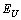 is the Urbach energy which is the value inverse to the absorption edge slope
is the Urbach energy which is the value inverse to the absorption edge slope 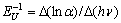 ;
; 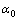 and
and 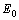 are coordinates of the convergence point of the Urbach “bundle”. The temperature behaviour of the Urbach energy
are coordinates of the convergence point of the Urbach “bundle”. The temperature behaviour of the Urbach energy 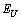 in the framework of the Einstein model is described by the equation[13]
in the framework of the Einstein model is described by the equation[13]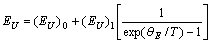 | (2) |
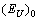 and
and 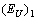 are constants,
are constants, 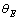 is the Einstein temperature which corresponds to the average frequency of phonon excitations of non-interacting oscillators. It is known that the Urbach energy in solids is determined not only by temperature, but also by structural disordering[14]:
is the Einstein temperature which corresponds to the average frequency of phonon excitations of non-interacting oscillators. It is known that the Urbach energy in solids is determined not only by temperature, but also by structural disordering[14]: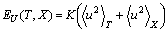 | (3) |
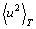 and
and 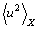 are mean-square deviations (displacements) of the atoms from their equilibrium positions, caused by the temperature disorder and the structural disorder of the solid-state system, respectively. As displacement of atoms from the equilibrium positions leads to a change in the electrical potential of the system, Eq. (3) can be written as
are mean-square deviations (displacements) of the atoms from their equilibrium positions, caused by the temperature disorder and the structural disorder of the solid-state system, respectively. As displacement of atoms from the equilibrium positions leads to a change in the electrical potential of the system, Eq. (3) can be written as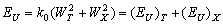 | (4) |
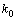 is a constant,
is a constant, 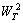 and
and 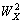 are mean-square deviations from the electric potential of a perfectly ordered structure, caused by the temperature and the structural disorder, respectively. The contributions of the temperature disordering
are mean-square deviations from the electric potential of a perfectly ordered structure, caused by the temperature and the structural disorder, respectively. The contributions of the temperature disordering 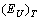 and structural disordering
and structural disordering 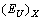 to the Urbach energy
to the Urbach energy 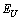 are considered independent, equivalent, and additive.
are considered independent, equivalent, and additive.3. Experimental
- Sn2Р2Se6 single crystals were obtained by chemical transport[15]. The studies were performed for the samples of different thickness d=30÷500 µm in a broad temperature range 77–350 K. The incident light was linearly polarized, the electric field strength vector oscillating in planes parallel to X (coinciding with[100] crystallographic direction), or Y ([010] crystallographic direction). For transmission and reflection measurements a LOMO MDR-3 grating monochromator was used. The instrumental width was near 1 Å. A UTREX cryostat was applied providing temperature stabilization within 0.1 K. The experimental setup and technique are described in Ref.[10].
4. Results and Discussion
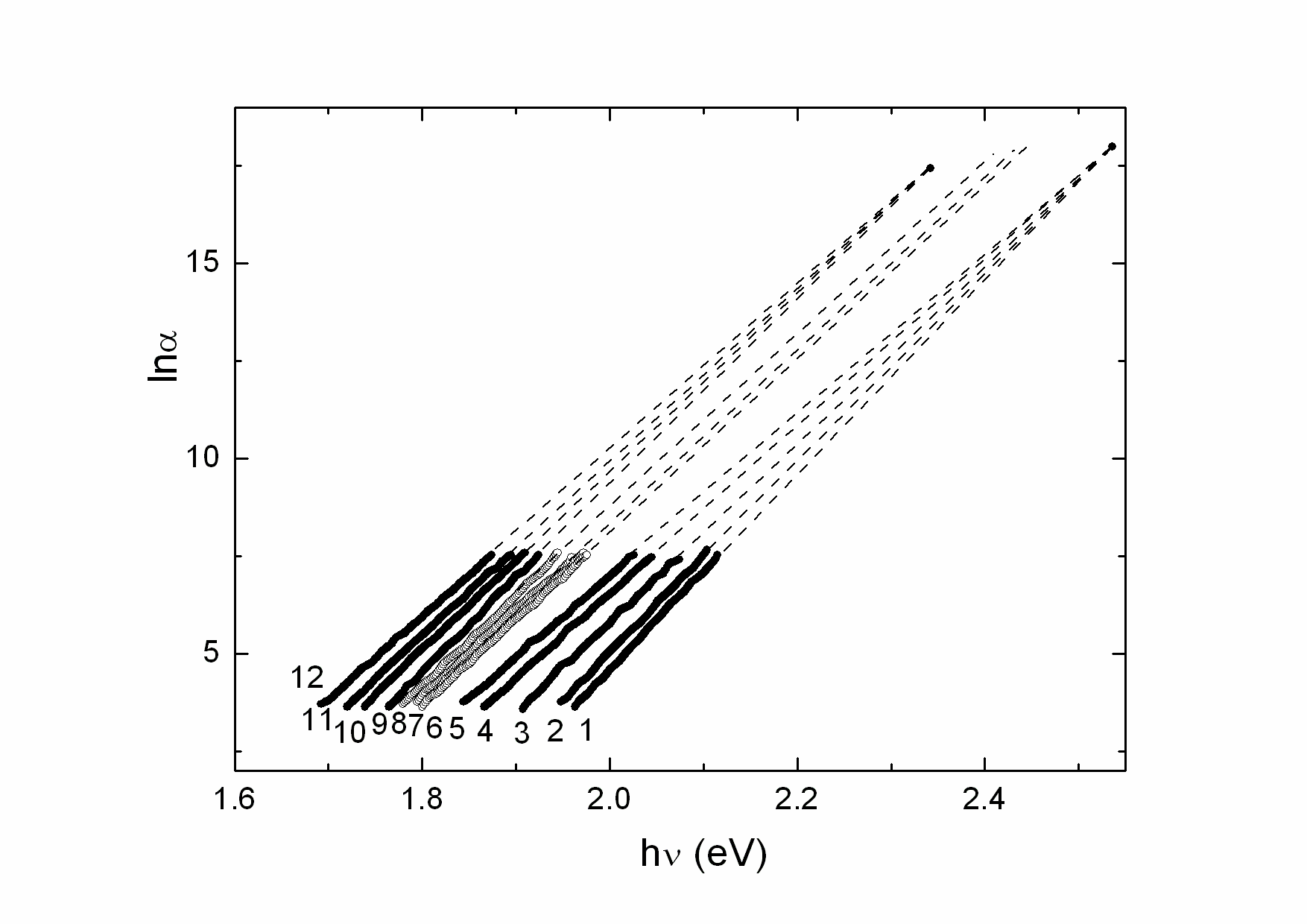
- The studies of optical absorption edge of Sn2P2Se6 ferroelectric have revealed three typical temperature ranges: (i) the range of the Urbach behaviour of the absorption edge at T<193 K, (ii) the range of parallel red shift of the optical absorption edge within the temperature interval 193≤T≤ 221 K and (iii) the range of the Urbach behaviour of the absorption edge at T>221 K (Fig.1). The parallel red shift of the optical absorption edge in Sn2Р2Se6 and, consequently, the temperature invariance of the Urbach energy
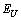 (Fig. 2), like in the case of other materials with modulated structures such as (PbySn1-y)2P2Se6[16], CdP2, α-ZnP2[17], (N(CH3)4)2ZnCl4[18] (N(CH3)4)2CuCl4[19], are related to the presence of the structure modulation in the incommensurate phase.
(Fig. 2), like in the case of other materials with modulated structures such as (PbySn1-y)2P2Se6[16], CdP2, α-ZnP2[17], (N(CH3)4)2ZnCl4[18] (N(CH3)4)2CuCl4[19], are related to the presence of the structure modulation in the incommensurate phase. | Figure 2. Temperature dependences of the Urbach energy EU for Sn2P2Se6 crystal. The insert shows the temperature dependence of the 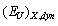 contribution contribution |
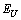 in the incommensurate phase (Fig. 2), we present the contribution of the structural disordering
in the incommensurate phase (Fig. 2), we present the contribution of the structural disordering 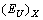 as a sum of two components – static structural disordering
as a sum of two components – static structural disordering 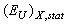 and dynamic structural disordering
and dynamic structural disordering 
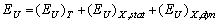 | (5) |
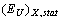 is caused by the presence of various defects, impurities and inhomogeneities of the crystal structure. Thus, in Ref.[20] it is shown that the most probable defects in Sn2P2Se6-type crystal lattice are the vacancies of Se atoms which result in the formation of deep levels in the band gap. The presence of the defects leads to the appearance of local non-uniform electrical fields which are revealed as the presence of a strong photorefractive effect and impurity-type photoconductivity[21, 22]. The contribution of the temperature-dependent dynamic structural disordering
is caused by the presence of various defects, impurities and inhomogeneities of the crystal structure. Thus, in Ref.[20] it is shown that the most probable defects in Sn2P2Se6-type crystal lattice are the vacancies of Se atoms which result in the formation of deep levels in the band gap. The presence of the defects leads to the appearance of local non-uniform electrical fields which are revealed as the presence of a strong photorefractive effect and impurity-type photoconductivity[21, 22]. The contribution of the temperature-dependent dynamic structural disordering 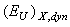 is caused by the presence of structure modulation in ferroics.The values of these contributions were determined from Eq. (2), the parameters
is caused by the presence of structure modulation in ferroics.The values of these contributions were determined from Eq. (2), the parameters 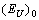 ,
, 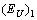 and Einstein temperature
and Einstein temperature 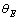 being obtained from the temperature dependence of the Urbach energy
being obtained from the temperature dependence of the Urbach energy 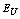 . The calculations and further analysis showed that in the commensurate paraelectric (T>Ti) and ferroelectric (T<Tc) phases the temperature behaviour of
. The calculations and further analysis showed that in the commensurate paraelectric (T>Ti) and ferroelectric (T<Tc) phases the temperature behaviour of 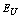 is determined by the temperature behaviour of the contribution
is determined by the temperature behaviour of the contribution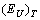 caused by lattice thermal vibrations, at a constant value of
caused by lattice thermal vibrations, at a constant value of 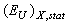 =const and in the absence of
=const and in the absence of 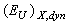 =0 (see Eq. (5)). In the incommensurate phase (Tc<T<Ti), with decreasing temperature the contribution of
=0 (see Eq. (5)). In the incommensurate phase (Tc<T<Ti), with decreasing temperature the contribution of 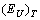 decreases; however, as the contribution
decreases; however, as the contribution 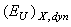 increases and the contribution of
increases and the contribution of 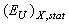 remains constant, the combination of these factors leads to the temperature invariability of the Urbach energy
remains constant, the combination of these factors leads to the temperature invariability of the Urbach energy 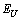 =const (see Eq. (5), Fig. 2) and to the parallel red shift of the absorption edge (Fig. 1). Dynamic structural disordering
=const (see Eq. (5), Fig. 2) and to the parallel red shift of the absorption edge (Fig. 1). Dynamic structural disordering 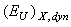 in the incommensurate phase is caused by the appearance of a modulation wave formed by displacement of tin atoms in (010) symmetry plane along a direction close to[100] (See Ref.[23]). With the temperature variation, the changes of the amplitude and the period of the modulation wave are observed whereas the direction of the modulation wave vector remains unchanged[23]. Thus, the temperature range for which the condition
in the incommensurate phase is caused by the appearance of a modulation wave formed by displacement of tin atoms in (010) symmetry plane along a direction close to[100] (See Ref.[23]). With the temperature variation, the changes of the amplitude and the period of the modulation wave are observed whereas the direction of the modulation wave vector remains unchanged[23]. Thus, the temperature range for which the condition 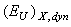 ≠0 becomes true and the parallel red shift of the optical absorption edge as well the temperature invariance of the Urbach energy
≠0 becomes true and the parallel red shift of the optical absorption edge as well the temperature invariance of the Urbach energy 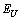 are observed, can be identified as the range of existence of the incommensurate phase in ferroics. The observed features of the absorption edge behaviour in the incommensurate phase of Sn2P2Se6 crystal are characteristic properties of incommensurate superstructures, similarly to the invar effect[24] and anomalous hysteresis[25].
are observed, can be identified as the range of existence of the incommensurate phase in ferroics. The observed features of the absorption edge behaviour in the incommensurate phase of Sn2P2Se6 crystal are characteristic properties of incommensurate superstructures, similarly to the invar effect[24] and anomalous hysteresis[25].5. Conclusions
- In Sn2P2Se6 ferroelectric, the dynamic structural disordering of the crystal lattice, the parallel red shift of optical absorption edge and the temperature invariance of Urbach energy are observed in the incommensurate phase in the temperature range 193≤T≤221 K. The presence of the dynamic structural disordering
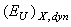 in the incommensurate phase of Sn2P2Se6 is caused by modulation wave, the parameters of which depend on temperature.
in the incommensurate phase of Sn2P2Se6 is caused by modulation wave, the parameters of which depend on temperature. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML