-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Condensed Matter Physics
p-ISSN: 2163-1115 e-ISSN: 2163-1123
2013; 3(5): 123-132
doi:10.5923/j.ajcmp.20130305.02
Elastic, Acoustical and Electronic Behaviour of the RM (R = Dy, Ho, Er; M=Cu, Zn) Compounds
R. P. Singh1, V. K. Singh1, R. K. Singh1, M. Rajagopalan2
1Department of Physics, Banaras Hindu University, Varanasi, India
2Department of Physics, Anna University, Chennai, India
Correspondence to: R. K. Singh, Department of Physics, Banaras Hindu University, Varanasi, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
First principle calculations using the full-potential augmented plane-waves plus local orbital (FP-APW + lo) within density-functional theory (DFT) have been carried out to study the elastic, acoustical and electronic properties of R-Cu and R-Zn (R= Dy, Ho, Er) intermetallic compounds. Acoustic velocities are found to increase for both groups of intermetallics. The band structure and density of states histograms are plotted. From the density of states (DOS) histograms, we find that total density of states (DOS) near Fermi level is mostly dominated by R-atom (R= Dy, Ho, Er, Tm) and DOS below the Fermi level are mainly due to “3d” orbital electrons of Cu (or Zn).
Keywords: Intermetallic Compounds, Elastic Properties, Acoustical Properties, Electronic Properties
Cite this paper: R. P. Singh, V. K. Singh, R. K. Singh, M. Rajagopalan, Elastic, Acoustical and Electronic Behaviour of the RM (R = Dy, Ho, Er; M=Cu, Zn) Compounds, American Journal of Condensed Matter Physics, Vol. 3 No. 5, 2013, pp. 123-132. doi: 10.5923/j.ajcmp.20130305.02.
Article Outline
1. Introduction
- Intermetallic compounds are a class of materials that are often characterized by high melting point, high specific strength, ductility, attractive high temperature mechanical properties, as well as good electrical and magnetic properties, which make them promising high temperature structural materials for aerospace applications. The high ductility and fracture toughness of intermetallics have made them useful for developing commercial aircraft turbines[1, 2]. Some of the properties of intermetallics, viz. ductility can be modified by making them off-stoichiometric or by doping with a suitable third element[3]. The study of the rare earth intermetallic compounds represents an important part of the more general problem of the metallic phases, particularly rare earths have peculiar electronic configuration (e.g. electron occupancy in f-shell results valence states etc). As one moves along the rare-earth groups in the periodic table, the atomic dimensions and electro-negativities change regularly. Therefore, combining these rare-earth (R) with transition metals (M: like Cu and Zn) results in a series of interesting intermetallics showing regularity in various properties. The rare earth intermetallics studied in the present work are R-Cu and R-Zn (where, R= Dy, Ho, Er). The intermetallics R-Cu and R-Zn are known to have CsCl type structure (bcc) which is often referred to as ‘B2’ type structure and have space group Pm3m[4, 5].In general, subject of RM intermetallics has long been studied. Many excellent books/reviews on intermetallics are available[3-4, 6-15]. Recent detailed analysis on RM intermetallics has given some interesting observations: (1) Presence of multiple phases apart from dominant CsCl type phase[16] (ii) Presence of dislocations[16] and (iii) Magnetic ordering[11, 17-20]. Because of the importance of rare earth intermetallics in aerospace engineering/machine parts, some studies have been carried out on mechanical (ductility, tensile strength etc) and elastic properties. Gschneidner et al.[3] presented an extensive study on rare earth intermetallic materials which were followed by many more studies[21, 22]. Gschneidner et al.[3] prepared a number of binary rare earth intermetallics out of which they focused on three compounds namely DyCu, YCu and YAg. These compounds were found to exhibit room temperature ductility. Samples were prepared by arc-melting high-purity elements to form compounds with a 50-50 atomic mix of Y or Dy and Ag or Cu. X-ray diffraction, optical metallographic and electron microscopy experiments confirmed the specimens were single-phase with the fully ordered B2 structure. DyCu, YAg, and YCu are the most extensively studied intermetallics compounds; All the three compounds display tensile ductility of 11 to 20% elongation.To verify that the large tensile elongations were indicative of high toughness, fracture-toughness tests were performed on samples of DyCu. The fracture-toughness values obtained for DyCu were similar to those for commercial aircraft aluminum alloys[3, 23-24]. Another subsequent study made by Zhang et al.[23], also examined further for the fracture toughness of polycrystalline YAg, YCu, and DyCu. Ductility in RM has been discussed in terms of Poisson’s ratio, defects, anisotropy factor etc. Literature survey indicates that, in spite of technological importance of these rare earth intermetallics, there is still a need for a systematic theoretical study of structural, elastic, electronic and acoustical properties of these materials for future applications. The present study is an attempt in this direction. First principle calculations have been carried out using DFT formalism within Linearized Full Potential Augmented Plane Wave plus local orbitals (FPLAPW + lo) method for rare earth intermetallics (R-Cu and R-Zn; R= Dy, Ho Er). Theoretical studies have been carried out to calculate the following properties: (a) Structural properties: Lattice parameter (a0), equilibrium bulk modulus (B0). (b) Elastic properties: Elastic constants (Cij), Bulk modulus (B), Young’s modulus (Y), Shear modulus (G) and Poisson’s ratio (v). (c) Acoustic parameters: Acoustic velocity for longitudinal and shear mode (VL and VS) and Debye average velocity (Vm). (d) Some other parameters: Debye temperature (θD), Grüneisen parameter (
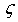 ) and density (ρ). (e) Electronic properties: Charge density distribution, Density of States (DOS) and Band Structure.Attempt has been made to establish a structure-property correlation. Particularly emphasis is to see how the properties change as one of the constitutent atoms is changed in a particular group of materials. For example the properties of R-Cu and R-Zn follow a sequential behavior as we change R from Dy→Ho→Er.
) and density (ρ). (e) Electronic properties: Charge density distribution, Density of States (DOS) and Band Structure.Attempt has been made to establish a structure-property correlation. Particularly emphasis is to see how the properties change as one of the constitutent atoms is changed in a particular group of materials. For example the properties of R-Cu and R-Zn follow a sequential behavior as we change R from Dy→Ho→Er.2. Computational Approach
- To compute the electronic structure and the basic ground state properties of R-Cu and R-Zn (R= Dy, Ho, Er), full-potential (linear) augmented plane wave plus local orbital (FP-APW+ lo) method has been used[25-28]. The valence part is treated within a potential expanded into spherical harmonics up to l=4. The valence wave functions inside the spheres are expanded up to lmax = 8. A plane-wave expansion with Rmt ·Kmax is taken to be 8. The K and E convergence are checked by increasing the number of K points and the energy convergence criteria. In the irreducible part of the Brillouin Zone, 10 х 10 х 10 K points were used to calculate the total and partial density of states. For each of these compounds the following basis orbitals were used as the valence states:
 The elastic constants (C11, C12 and C44) have been calculated by means of crystal strained method[29]. Using the three elastic constants, the elastic parameters viz. bulk modulus (B) Young’s modulus (Y) isotropic shear modulus (G) and Poisson ratio, (
The elastic constants (C11, C12 and C44) have been calculated by means of crystal strained method[29]. Using the three elastic constants, the elastic parameters viz. bulk modulus (B) Young’s modulus (Y) isotropic shear modulus (G) and Poisson ratio, (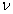 ) can be calculated using the following explicit expressions[30, 31]:
) can be calculated using the following explicit expressions[30, 31]: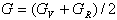 | (1) |
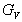 is Voigt’s shear modulus corresponding to the upper bound of G values, and
is Voigt’s shear modulus corresponding to the upper bound of G values, and 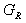 is Reuss’s shear modulus for cubic crystals corresponding to the lower bound values, expressed as:
is Reuss’s shear modulus for cubic crystals corresponding to the lower bound values, expressed as: 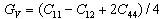 | (2) |
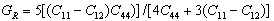 | (3) |
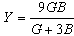 | (4) |
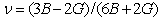 | (5) |
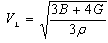 | (6) |
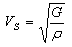 | (7) |
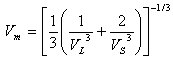 | (8) |
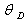 [33] and Grüneisen parameter,
[33] and Grüneisen parameter, 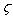 [34] are sound velocity and mass density dependent, which are calculated using the expressions given by
[34] are sound velocity and mass density dependent, which are calculated using the expressions given by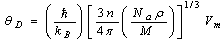 | (9) |
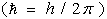 and n, Na, ρ and M,
and n, Na, ρ and M, 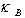 are the number of atoms in the molecule, Avogadro’s number, mass density, molecular weight and Boltzmann constant respectively.The Grüneisen parameter (which provides anharmonicity) of crystals is given by:
are the number of atoms in the molecule, Avogadro’s number, mass density, molecular weight and Boltzmann constant respectively.The Grüneisen parameter (which provides anharmonicity) of crystals is given by: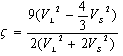 | (10) |
3. Results and Discussion
3.1. Structural Properties
- In the present study, we report the investigations on the ground state structural properties viz. lattice parameter (ao), bulk modulus (Bo) and its first order pressure derivative (B0’) for the rare earth intermetallic compounds (RM, R=Dy, Ho, Er and M= Cu, Zn). Total energy calculations can be used conveniently to determine the equilibrium structure of a system. The configuration of the lowest energy has been determined by comparing the total energy for different possible configurations.The bulk properties of a crystalline material can accordingly be determined by calculating the total energy as a function of cell volume. Structural properties viz. lattice parameter (ao), bulk modulus (Bo) and its first order pressure derivative (B0’) are calculated by fitting the total energy according to the Birch-Murnaghan's equation of state[35, 36] given by:
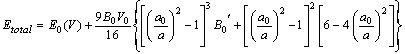 | (11a) |
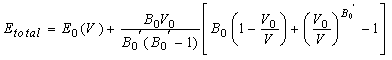 | (11b) |
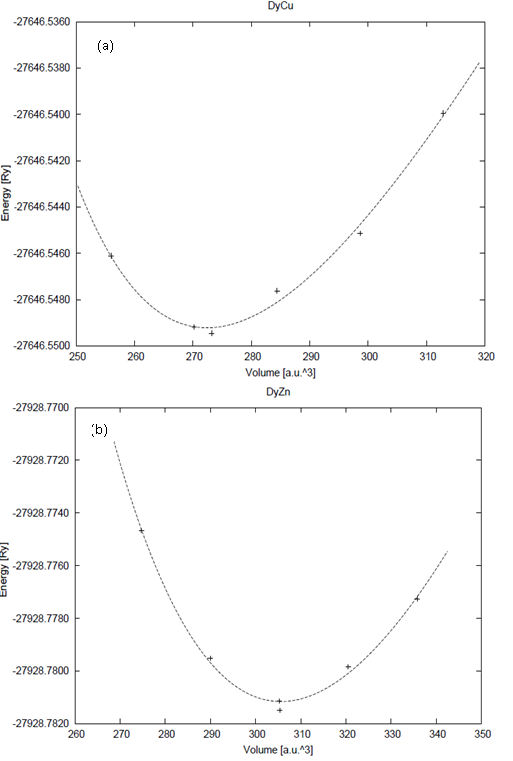 | Figure 1. Total equilibrium energy as a function of volume for (a) DyCu and (b) DyZn with GGA calculation |
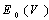 and
and 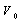 are the energy and volume at equilibrium.
are the energy and volume at equilibrium. 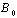 and
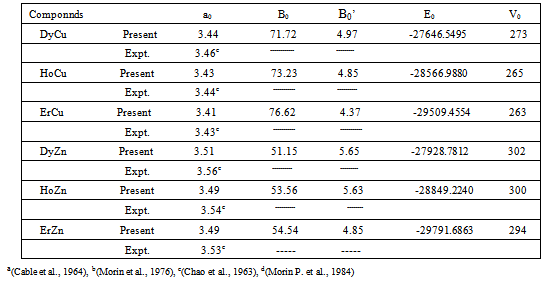
and 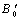 are the equilibrium bulk modulus and its first order pressure derivative.The energy vs. volume curve has been shown for DyCu and DyZn in Figures 1(a) and 1(b) respectively (while for others R-Cu and R-Zn compound only the equilibrium energy and volume have been shown in Table 1). It is obvious from Figures 1(a) and 1(b) and Table 1 that equilibrium volume and lattice parameters decrease as we go from DyCu to ErCu (or DyZn to ErZn) due to increasing f-orbital electrons from DyCu to ErCu (or DyZn to ErZn) (i.e. bonding states are being filled). Calculated ground state lattice parameter (ao), bulk modulus (Bo) and its first order pressure derivative (B0’), obtained using GGA approximation are shown in Table 1. Calculated values of ao and B0 for R-Cu and R-Zn are found to be in good agreement with available experimental values[7, 8, 37].
are the equilibrium bulk modulus and its first order pressure derivative.The energy vs. volume curve has been shown for DyCu and DyZn in Figures 1(a) and 1(b) respectively (while for others R-Cu and R-Zn compound only the equilibrium energy and volume have been shown in Table 1). It is obvious from Figures 1(a) and 1(b) and Table 1 that equilibrium volume and lattice parameters decrease as we go from DyCu to ErCu (or DyZn to ErZn) due to increasing f-orbital electrons from DyCu to ErCu (or DyZn to ErZn) (i.e. bonding states are being filled). Calculated ground state lattice parameter (ao), bulk modulus (Bo) and its first order pressure derivative (B0’), obtained using GGA approximation are shown in Table 1. Calculated values of ao and B0 for R-Cu and R-Zn are found to be in good agreement with available experimental values[7, 8, 37].3.2. Elastic Properties
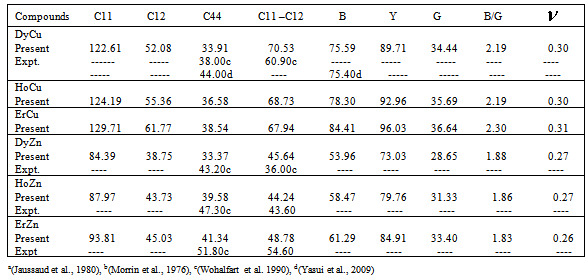
- The calculated values of elastic moduli (Cij) along with Bulk modulus (B), Young’s modulus (Y), isotropic shear modulus (G), B/G ratio and Poisson’s ratio,
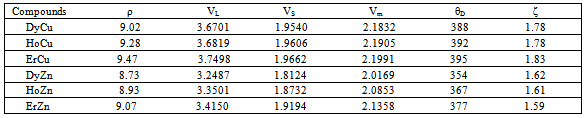
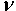 at equilibrium for RM intermetallics (R=Dy, Ho, Er and M= Cu, Zn) using PBE-GGA approximations have been given in Tables 2. Experimental values of C11 - C12 and C44 determined by ultrasonic measurement techniques[10, 37-39] for DyCu, DyZn, HoZn, ErZn compounds are available in literature, which show close agreement with present calculated values.Values of Cij, B, Y and G are increasing in R-Cu and R-Zn intermetallic series as R changes in sequence Dy → Ho → Er. Our C44 and C11-C12 values are underestimated and overestimated respectively by about ∼15% and ∼22 % respectively for DyCu compared to the experimental value of Wohalfarath et al.[10], while C44 value is underestimated by about ∼14% to the experimental value of Yasui et al.[39]. Present value of bulk modulus for DyCu is in close agreement with available experimental value of Yasui et al.[39].Present C44 and C11-C12 values for DyZn and HoZn are underestimated and overestimated respectively by ∼30%, ∼20%; and ∼20%, ∼1%, while for ErZn, these values are underestimated by ∼19% and ∼11% respectively compared to the experimental values of Wohalfarth et al.[10]. The minor difference between experimental values and our calculated values may be attributed to the reason that available experimental values are given at room temperature, while our values are in equilibrium state. Furthermore, the structural stability conditions (C11 - C12 > 0, C11 > 0, C44 > 0, C11 + 2C12 > 0) are satisfied for calculated elastic moduli[40]. Besides above stability conditions, present calculated elastic moduli satisfy the condition C12 < B < C11 (applicable to cubic systems). This gives credence to our calculated values of elastic moduli.The B/G value is an index of ductility for metallic / intermetallic materials, proposed by Pugh[41] to predict brittle or ductile behaviors of the materials. If B / G > 1.75, then ductile behavior is predicted, otherwise, the material behavior is brittle in manner. The B/G ratio of R-Cu and R-Zn compounds is greater than 1.75 (Tables 2). Therefore, all RM compounds are ductile and R-Cu compounds are more ductile than R-Zn compounds as R-Cu compounds have large value of B/G than R-Cu. The calculated data on acoustic velocities (VL and VS and Vm), Debye temperature (θD), Grüneisen parameter (
at equilibrium for RM intermetallics (R=Dy, Ho, Er and M= Cu, Zn) using PBE-GGA approximations have been given in Tables 2. Experimental values of C11 - C12 and C44 determined by ultrasonic measurement techniques[10, 37-39] for DyCu, DyZn, HoZn, ErZn compounds are available in literature, which show close agreement with present calculated values.Values of Cij, B, Y and G are increasing in R-Cu and R-Zn intermetallic series as R changes in sequence Dy → Ho → Er. Our C44 and C11-C12 values are underestimated and overestimated respectively by about ∼15% and ∼22 % respectively for DyCu compared to the experimental value of Wohalfarath et al.[10], while C44 value is underestimated by about ∼14% to the experimental value of Yasui et al.[39]. Present value of bulk modulus for DyCu is in close agreement with available experimental value of Yasui et al.[39].Present C44 and C11-C12 values for DyZn and HoZn are underestimated and overestimated respectively by ∼30%, ∼20%; and ∼20%, ∼1%, while for ErZn, these values are underestimated by ∼19% and ∼11% respectively compared to the experimental values of Wohalfarth et al.[10]. The minor difference between experimental values and our calculated values may be attributed to the reason that available experimental values are given at room temperature, while our values are in equilibrium state. Furthermore, the structural stability conditions (C11 - C12 > 0, C11 > 0, C44 > 0, C11 + 2C12 > 0) are satisfied for calculated elastic moduli[40]. Besides above stability conditions, present calculated elastic moduli satisfy the condition C12 < B < C11 (applicable to cubic systems). This gives credence to our calculated values of elastic moduli.The B/G value is an index of ductility for metallic / intermetallic materials, proposed by Pugh[41] to predict brittle or ductile behaviors of the materials. If B / G > 1.75, then ductile behavior is predicted, otherwise, the material behavior is brittle in manner. The B/G ratio of R-Cu and R-Zn compounds is greater than 1.75 (Tables 2). Therefore, all RM compounds are ductile and R-Cu compounds are more ductile than R-Zn compounds as R-Cu compounds have large value of B/G than R-Cu. The calculated data on acoustic velocities (VL and VS and Vm), Debye temperature (θD), Grüneisen parameter (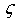 ) for R-Cu and R-Zn which are important to describe anharmonic properties of the compounds have been given in Table 3. The calculated values of mass density (ρ) for R-Cu and R-Zn have also been given in Table 3.
) for R-Cu and R-Zn which are important to describe anharmonic properties of the compounds have been given in Table 3. The calculated values of mass density (ρ) for R-Cu and R-Zn have also been given in Table 3.
|
|
3.3. Electronic Properties
- DFT calculations determine the ground state electron density in the material which provides information about the location of electrons in the system. The charge distribution reveals, for instance, if the valence electrons are evenly distributed as in simple metals or highly concentrated to the host ions as in ionic materials. Even more interesting is the difference between charge densities of two similar systems. This can be used to investigate electron accumulation at particular places in the material e.g. near defects, surfaces or grain boundaries. The results on charge density calculations are necessary to determine the character of chemical bonds between elements.In order to investigate the bonding properties of rare earth intermetallics (RM, R= Dy, Ho, Er and M= Cu, Zn), valance charge density distribution in the (100) plane has been plotted in Figures 2 (a) and 2 (b) for DyCu and DyZn respectively (charge density distribution plots for remaining R-Cu and R-Zn compound have not been shown as they show similar features). Three-dimensional representations of valance charge density distribution for DyCu and DyZn have been shown in Figures 3 (a) and 3 (b) respectively. The charge density distribution shows spherically symmetric concentration centered on R (R = Dy, Ho, Er) and Cu, Zn atoms. It can also be seen from the charge density distribution (Figures 2 (a) and 2 (b) and Figures 3 (a) and 3 (b)) that charge density in the vicinity of Cu (or Zn) is larger compared to the rare earth counterpart due to the fact that d orbitals of Cu (or Zn) contribute dominantly in R-Cu (or R-Zn), which can be seen from density of states shown in Figures 4 and 5 for DyCu and DyZn respectively. Thus, it may be concluded that electron charge density in R-Cu and R-Zn is mainly due to “d” orbital electrons of Cu (or Zn). Furthermore, Total density of states for DyCu, Dy and Cu, and partial density of states plots for “s”, “p” and “d” states for Dy and Cu and “f” states of Dy have been shown in Figures 4 (a-e), while total density of states for DyZn, Dy and Zn and partial density of states plots for “s”, “p” and “d” states for R and Zn and “f” states of Dy have been shown in Figures 5(a- e). The dotted line at 0 eV shows Fermi level. (The DOS plots for remaining R-Cu and R-Zn compound have not been shown as they show similar features). It can be seen from Figures 4 (a- e) and 5 (a-e) that the DOS mostly lie in the energy range approximately between -5 eV to 0 eV for R-Cu and nearly between -7 eV to 0 eV for R-Zn. It is obvious that DOS near Fermi level are mostly dominated by Dy (or Ho or Er ) (see green line contribution) and DOS below the Fermi level are mostly dominated by Cu (or Zn) (see blue line contribution). Furthermore, Figures 4 (d) and 5 (d) also show that DOS below Fermi level are mainly due to “3d” orbital electrons of Cu (or Zn). In case of R-Cu, the peak below Fermi level at around -3eV shows strong hybridization of Cu-s and Cu-d states while, in case of R-Zn, the peak below Fermi level at around -7 eV is due to Zn-d states. Therefore, it can be concluded that out of s, p, d and f-partial density of states of R, Cu and Zn in R-Cu and R-Zn, d states of Cu and Zn have the dominant character. Thus, d-states of Cu (or Zn) contribute dominantly to the electronic conduction in R-Cu and R-Zn compounds. Again, In case of R-Cu and R-Zn, it has been found that near Fermi level, total DOS for R atoms increases from Dy to Er which is the effect of increasing of number of f-orbital electrons from Dy to Er. The Kohn-Sham eigenvalues extracted from DFT calculation can be used to determine band structure of the system. The bands can be considered as the collection of the individual energy levels of electrons surrounding each atom. The electron band gap energy of a solid describes ranges of energy that an electron is forbidden to have. It is due to the diffraction of the quantum mechanical electron waves in the periodic crystal lattice. The band structure of a material determines several characteristics such as understanding the concept of an energy band gap and material character.The electron dispersion curve along high symmetry direction in the Brilloun zone (Band structure) for DyCu and DyZn have been shown in Figures 6(a) and 1(a) respectively (electron dispersion plots for remaining R-Cu and R-Zn compound have not been shown in as they show similar features). From Figures 6 (a) and 6 (b), it is obvious that conduction and valence bands are overlapping near the Fermi level, reflecting metallic character of R-Cu (or R-Zn). Most of Valence band states are lying in energy range -5eV to 0 eV and -7 eV to 0 eV for DyCu and DyZn respectively. This can be seen also from the corresponding DOS Figures 4 (a-e) for DyCu and 5 (a- e) for DyCu and DyZn respectively.
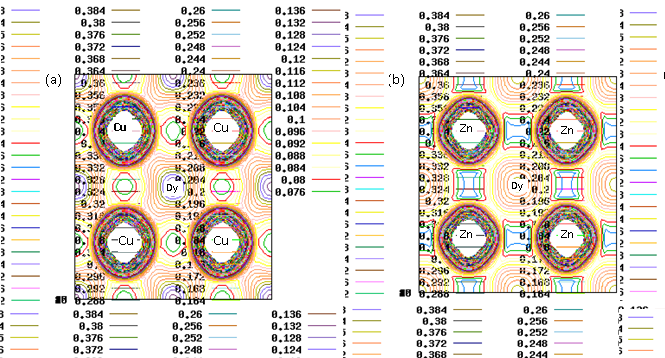 | Figure 2. Contour plot of the total valance charge density in the (100) plane for (a) DyCu (b) DyZn |
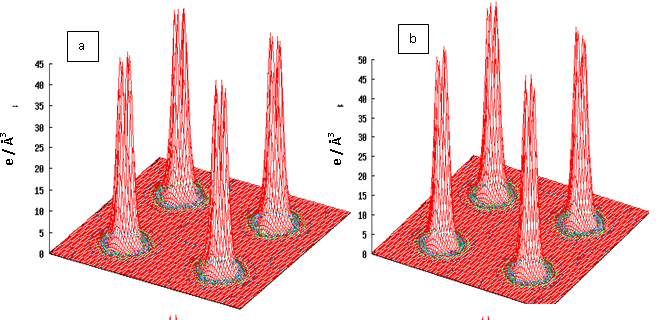 | Figure 3. 3-dimentional plots of the total valance charge density in the (100) plane for (a) DyCu (b) DyZn |
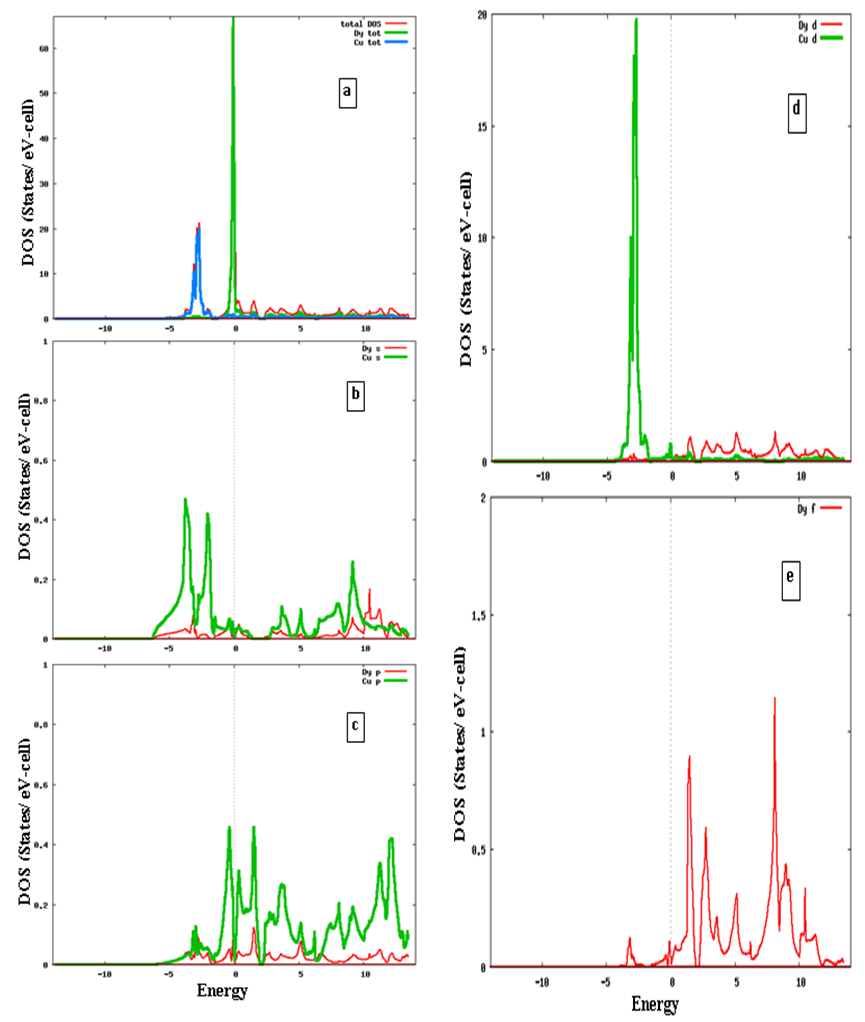 | Figure 4. Calculated density of states (a) total density of states for DyCu, Dy and Cu (b) density of s-states for Dy and Cu (c) density of p-states for Dy and Cu (d) density of d-states for Dy and Cu (e) density of f-states for Dy |
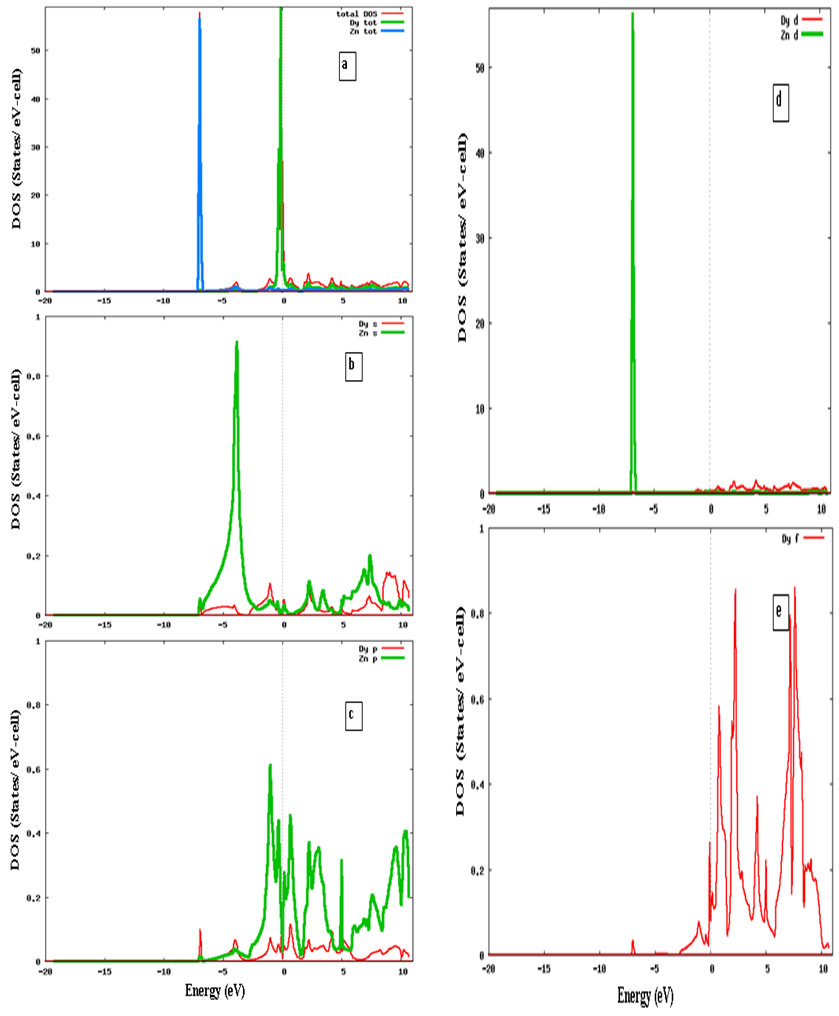 | Figure 5. Calculated density of states (a) total density of states for DyZn, Dy and Zn (b) density of s-states for Dy and Zn (c) density of p-states for Dy and Zn (d) density of d-states for Dy and Zn (e) density of f-states for Dy |
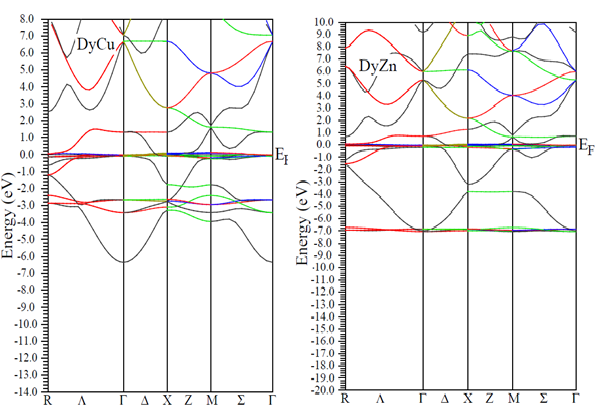 | Figure 6. Electron dispersion curves along high symmetry direction in the Brilloun zone for DyCu and DyZn with GGA calculation |
4. Conclusions
- First principles calculations have been carried out to study the structural parameters (viz. a0, B0’), second order elastic constants (Cij), electronic properties (viz. charge density distribution, density of states, band structure), acoustical parameters (viz. VL, VS, Vm) and some other parameters (viz. Debye temperature, θD Grüneisen parameter,
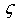 and density, ρ) of CsCl type compounds, R-Cu and R-Zn (R= Dy, Ho, Er). The following conclusions have been drawn from the calculations;(a) Structural parameters (a0, B0 and B0’) and elastic constants (Cij) are in good agreement with available experimental literature values.(b) Calculated elastic constants obey the structural stability conditions (C11 - C12 > 0, C11 > 0, C44 > 0, C11 + 2C12 > 0) and (C12 < B < C11.) which gives credence to our calculated values.(c) Acoustic velocities (VL, VS and Vm) increase for both group of intermetallics viz. R-Cu and R-Zn.(d) B/G ratio > 1.75, so, ductile character of R-Cu and R-Zn predicted and R-Cu are more ductile compared to corresponding member of R-Zn.(e) The charge density in the vicinity of Cu (or Zn) is larger than that of R atoms (R= Dy, Ho, Er).(f) Total density of states (DOS) near Fermi level is mostly dominated by R-atom and DOS below the Fermi level are mostly dominated by Cu (or Zn).(g) Partial density of states for R-Cu (or R-Zn) shows that DOS below Fermi level are mainly due to “3d” orbital electrons of Cu (or Zn).(h) Electronic conduction in R-Cu and R-Zn compounds is due to “3d” orbital electrons. (i) In band structure diagram, conduction and Valence bands are overlapping near the Fermi level which reflects metallic character of R-Cu and R-Zn.
and density, ρ) of CsCl type compounds, R-Cu and R-Zn (R= Dy, Ho, Er). The following conclusions have been drawn from the calculations;(a) Structural parameters (a0, B0 and B0’) and elastic constants (Cij) are in good agreement with available experimental literature values.(b) Calculated elastic constants obey the structural stability conditions (C11 - C12 > 0, C11 > 0, C44 > 0, C11 + 2C12 > 0) and (C12 < B < C11.) which gives credence to our calculated values.(c) Acoustic velocities (VL, VS and Vm) increase for both group of intermetallics viz. R-Cu and R-Zn.(d) B/G ratio > 1.75, so, ductile character of R-Cu and R-Zn predicted and R-Cu are more ductile compared to corresponding member of R-Zn.(e) The charge density in the vicinity of Cu (or Zn) is larger than that of R atoms (R= Dy, Ho, Er).(f) Total density of states (DOS) near Fermi level is mostly dominated by R-atom and DOS below the Fermi level are mostly dominated by Cu (or Zn).(g) Partial density of states for R-Cu (or R-Zn) shows that DOS below Fermi level are mainly due to “3d” orbital electrons of Cu (or Zn).(h) Electronic conduction in R-Cu and R-Zn compounds is due to “3d” orbital electrons. (i) In band structure diagram, conduction and Valence bands are overlapping near the Fermi level which reflects metallic character of R-Cu and R-Zn.ACKNOWLEDGEMENTS
- The authors thankfully acknowledge to Prof. P. Blaha for providing the WIEN2k code.
References
| [1] | A. M. Russell, Adv. Engg. Mat. 5 (2003) 629. |
| [2] | A. M. Russell, Z. Zhang, T. A. Lograsso, C. H. C. Lo, A. O. Pecharsky, J. R. Morris, Y. Y. Ye, K. A. Gschneidner Jr. and A. J. Slager, Acta Mater. 52, (2004) 4033. |
| [3] | K. A. Gschneidner Jr., A. M. Russell, A. O. Pecharsky, Z. Zhang, T. A. Lograsso, J. R. Morris, D. K. Hsu, C. H. C. Lo, Y. Y. Ye, A. J. Slager, D. C. Kesse, Nature Mater. 2 (2003) 591. |
| [4] | K.A. Gschneidner Jr., A. M. Russell, S. B. Biner, C.H.C. Lo, T. A. Lograsso, Y. Ye, D. Barnard, A. O. Tsokol, U. S. Department of Energy, Basic Energy Science (2004). |
| [5] | K. A. Gschneidner Jr., A. M. Russell, S. B. Biner, B. N. Harmon, D. K. Hsu, C. H. C. Lo, T. A. Lograsso, A. O. Pecharsky. U. S. Department of Energy, Basic Energy Science (2005). |
| [6] | W. J. Cable, W. C. Koehler, E. O. Wollan, Phys. Rev. 136 (1964) A240. |
| [7] | C. C. Chao, H. L. Luo, P. Duwez, J. Appl. Phys. 34 (1963) 1971. |
| [8] | P. Morin, S. J. Williamson, Phys. Rev. B 29 (1984) 1425. |
| [9] | P. Morin, J. Rouchy, E. Du Tremolet de Lacheisserie, Phys. Rev. B 16 (1977) 3182. |
| [10] | E. P. Wohalfarth, K. H. J. Buschow, 5 (1990) ISBN: 978-0-444-87477-1. |
| [11] | Y. N. Berdovsky, Nova Science Publishers, Inc. New York, (2008). |
| [12] | Y. R. Morris, Y. Y. Ye, Y. B. Lee, B. N. Harmon, K. A. Gschneidner Jr., A. M. Russell, Acta. Mater. 52 (2004) 4849. |
| [13] | A. R. Cause, E. Teghtsoonian, Matell. Trans. 1 (1970) 1177. |
| [14] | J. Rusz, I. Turek, M. Divis, Physica B 381 (2006) 265. |
| [15] | J. B. Sousa, P. P. Pinto, M. M. Amado, I. M. Moreira, M. E. Braga, P. Morin, M. Ausloos, J Phys F: Met Phys 10 (1980) 1809. |
| [16] | G. H. Cao, D. Shechtman, D.M. Wu, A.T. Becker, L.S. Chumbley, T.A. Lograsso, A. M. Russell, K. A. Gschneidner, Acta Mater. 55 (2007) 3765. |
| [17] | C. Chang-Chih, J. Appl. Phys. 37 (1966) 2081. |
| [18] | J. M. D. Coey, J. Appl. Phys. 49 (1978) 1646. |
| [19] | N. Heiman, N. Kazama, J. Appl. Phys. 49 (1978) 1686. |
| [20] | B. Tissier, R. Buder, J. M. D. Coey, J. Magn. and Magn. Mater. 15 (1980)1393. |
| [21] | A. S. Chernyshov, A. O. Tsokol, A. M. Tishin, K. A. Gschneidner Jr., V. K. Pecharsky, Phys. Rev. B 71 (2005) 184410. |
| [22] | V. K. Pecharsky, K. A. Gschneidner Jr., Intern. J. Refrig. 29 (2006) 1239. |
| [23] | Z. Zhang, A. M. Russell, S. B. Biner, K. A. Gschneidner Jr., C. H. C. Lo, Intermetallics 13 (2005) 559. |
| [24] | Oak Ridge National Laboratory, Status and Progress Report, Union Carbide Corporation for the U.S. Atomic Energy Commission (1964). |
| [25] | J. P. Perdew and K. Burke, Phys. Rev. Lett. 77 (1996) 3865. |
| [26] | E. Sjostedt, L. Nordstrom, D. J. Singh, Sol. Stat. Commun 114 (2000)15. |
| [27] | K. Schwarz, P. Blaha, G. K. H. Madsen, Comput. Phys. Commun. 147 (2002) 71. |
| [28] | H. J. Monkhorst, J. D. Pack, Phys. Rev. B 13 (1976) 5188. |
| [29] | T. Charpin, Laboratory of geometrix F-75252 Paris, France A package for Calculating elastic tensors of cubic phase using WIEN (2001). |
| [30] | M. Moakafi, R. Khenata, A. Bouhemadou, F. Semari, A. H. Reshak, M. Rabah. Comput. Mat. Sci. 46 (2009)1051. |
| [31] | F. Kalarasse, L. Kalarasse, B. Bennecer, A. Mellouki. Comput. Mat. Sci. 47 (2010) 869. |
| [32] | P. V. Reddy, M. B. Reddy, V. N. Muley, K. B. Reddy, Y. V. Ramana. J. Mat. Sc. Lett. 7(1988) 1243 |
| [33] | R.P. Singh, R.K. Singh, M. Rajagopalan, Intermetallics 19 (2011) 1359. |
| [34] | V. N. Belomestnykh, Tech. Phys. Lett. 30 (2) (2004) 91. |
| [35] | F. Birch, Phys. Rev. 71 (1947) 809. |
| [36] | F. D. Murnaghan, Proc. Nat. Acad. Sci. U.S.A 30 (1944) 244. |
| [37] | P. Morin, A. Waintal, B. Luthi, Phys. Rev. B. 14 (1976) 2972. |
| [38] | C. Jaussaud, P. Morin and D. Schmitt, J. Magnetism and Mag. Mat. 22 (1980) 98. |
| [39] | F. El Haj Hassan, A. Zaoui, W. Sekkal, Mat. Sci. and Engg. B87 (2001) 40. |
| [40] | M. Yasui, T. Terai, T. Kakeshita, M. Hagiwara, J. Phys. Conf. series 165 (2009) 012059. |
| [41] | S. F. Pugh, Philos. Mag. 45, (1954) 823. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML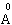 ), bulk modulus, B0 (GPa), its pressure derivative, B0' , equilibrium energy (Ryd) and equilibrium volume (Au^3) for RM intermetallics obtained using GGA functional
), bulk modulus, B0 (GPa), its pressure derivative, B0' , equilibrium energy (Ryd) and equilibrium volume (Au^3) for RM intermetallics obtained using GGA functional