-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Condensed Matter Physics
p-ISSN: 2163-1115 e-ISSN: 2163-1123
2013; 3(1): 1-8
doi:10.5923/j.ajcmp.20130301.01
Electronic, Elastic Structure and Phase Stability of TaRu Shape Memory Alloys
A. A. Mousa1, J. M. Khalifeh2, B. A. Hamad2
1Civil Engineerin Department, Middle East University, Amman, 11831, Jordan
2Physics Department, The University of Jordan, 11942, Amman, Jordan
Correspondence to: A. A. Mousa, Civil Engineerin Department, Middle East University, Amman, 11831, Jordan.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The phase stability and electronic structure of TaRu shape memory alloys are studied using full-potential linearized augmented plane wave method (FP-LAPW) on the basis of the density functional theory (DFT). The calculated equilibrium volumes are about 32 Å3and 30 Å3 for β-, 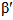 and β phases using the generalized gradient approximation (GGA) and local density approximation (LDA), respectively, in good agreement with the experimental values. The β-phase is favored by about 85 meV/f.u. than the β-phase. The value of the density of states at the Fermi energy, confirms that the β phase is the ground state equilibrium phase of TaRu at low temperatures, in agreement with the experimental findings.
and β phases using the generalized gradient approximation (GGA) and local density approximation (LDA), respectively, in good agreement with the experimental values. The β-phase is favored by about 85 meV/f.u. than the β-phase. The value of the density of states at the Fermi energy, confirms that the β phase is the ground state equilibrium phase of TaRu at low temperatures, in agreement with the experimental findings.
Keywords: Ta, Ru, DFT, Shape Memory Alloys, Bulk Modulus, Formation Energy
Cite this paper: A. A. Mousa, J. M. Khalifeh, B. A. Hamad, Electronic, Elastic Structure and Phase Stability of TaRu Shape Memory Alloys, American Journal of Condensed Matter Physics, Vol. 3 No. 1, 2013, pp. 1-8. doi: 10.5923/j.ajcmp.20130301.01.
Article Outline
1. Introduction
- Some metals that can remember their original shape and return to it when they are heated above a certain temperature are called the shape memory alloys (SMAs). The SMAs have two stable phases - the high-temperature phase, called austenite (the stronger high temperature phase) and the low-temperature phase, called martensite (the more deformable, lower temperature phase). Many SMAs have martensitic transformation below 200◦ C[1], so they are not suitable for high-temperature applications such as nuclear reactors, rockets and automotive engines[2]. So it is necessary to develop SMAs that have martensitec transformation more than 500 ◦C, called high temperature shape memory alloys[HTSMAs][3, 4]. The HTSMAs are attracting scientists in the field of shape memory and superelastic technology. They are suitable for high-temperature applications such as those listed above[1, 2, 5, 6]. Tantalum Ruthenium (TaRu) is an example of such alloys[3]. These alloys exhibit ordered CsCl-type
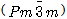 cubic structure (β-phase) for temperatures above 1100°C. Below 1100ºC, the crystal transforms to a tetragonal structure, called the β'-phase. When the temperature goes to less than 800ºC, the crystal transforms to a monoclinic structure (β"-phase)[3-9]. These alloys undergo transformations between the three different phases by changing the temperature, which is accompanied by changes in the electronic and elastic properties.Few studies have been carried out on TaRu alloys[10]. However, to the best of our knowledge this is the first attempt to study the structural and electronic properties of TaRu alloys using ab-initio calculations. In this work, we evaluate the angle of the monoclinic structure, which is not available experimentally, and calculate the elastic constants for the cubic structure.This paper is prepared as follows: In section two, we present the method of calculation. In section three, we present the results and discussion and the conclusions are outlined in section four.
cubic structure (β-phase) for temperatures above 1100°C. Below 1100ºC, the crystal transforms to a tetragonal structure, called the β'-phase. When the temperature goes to less than 800ºC, the crystal transforms to a monoclinic structure (β"-phase)[3-9]. These alloys undergo transformations between the three different phases by changing the temperature, which is accompanied by changes in the electronic and elastic properties.Few studies have been carried out on TaRu alloys[10]. However, to the best of our knowledge this is the first attempt to study the structural and electronic properties of TaRu alloys using ab-initio calculations. In this work, we evaluate the angle of the monoclinic structure, which is not available experimentally, and calculate the elastic constants for the cubic structure.This paper is prepared as follows: In section two, we present the method of calculation. In section three, we present the results and discussion and the conclusions are outlined in section four.2. Computational Method
- We performed self-consistent calculations using the full-potential linearized augmented plane wave (FP-LAPW) approach based on density functional theory (DFT)[11] as implemented in Wien2k[12]. In this method, the wave function, charge density and potential are expanded by spherical harmonic functions inside non overlapping spheres surrounding the atomic sites (muffin-tin spheres) and by a plane wave basis set in the remaining space of the unit cell (interstitial region). The calculated total energies are fitted to the Murnaghan equation of state[13] to obtain the energy-volume relation; and hence the lattice constants and bulk modulii are evaluated. The structures are fully relaxed using the damped Newton dynamics method to find the equilibrium atomic positions. The exchange correlation potential was treated using two methods: the generalized gradient approximation (GGA-PBE)[14] and local density approximation (LDA)[15]. The unit cells contain two atoms in the cubic CsCl structure (β phase), four atoms in the tetragonal L10 (β' phase) and monoclinic structures B19' (β" phase). The calculations are performed with a (12×12×12) Monkhorst-Pack (MP) k-point mesh for the cubic structure (space group
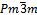 ), a (12×12×10) MP k-point mesh for tetragonal (space group P4/mmm) and (8×12×8) MP k-point mesh for monoclinic structures (space group P2/m), corresponding to 56 k points in the
), a (12×12×10) MP k-point mesh for tetragonal (space group P4/mmm) and (8×12×8) MP k-point mesh for monoclinic structures (space group P2/m), corresponding to 56 k points in the 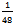 irreducible BZ of the simple cubic cell, 105 k points in the
irreducible BZ of the simple cubic cell, 105 k points in the 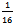 irreducible BZ of the tetragonal cell and 192 k points in the
irreducible BZ of the tetragonal cell and 192 k points in the 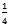 irreducible BZ of the monoclinic cell. In each case, we performed geometrical optimization followed by self-consistent calculations to obtain the partial densities of states (DOS) for all structures using the tetrahedron method with Blöchl corrections[16].The maximum quantum number ℓ for the wave function expansion inside the atomic spheres is confined to ℓ max = 10. The core cutoff energy is -81.66 eV and the plane wave cutoff, Kmax = 8/Rmt (Rmt is the smallest muffin-tin radius in the unit cell) is chosen for the expansion of wave functions in the interstitial region. The charge density is Fourier expanded up to Gmax = 12. The Rmt values for TaRu are chosen to be 2.2 a.u. for both Ta and Ru.
irreducible BZ of the monoclinic cell. In each case, we performed geometrical optimization followed by self-consistent calculations to obtain the partial densities of states (DOS) for all structures using the tetrahedron method with Blöchl corrections[16].The maximum quantum number ℓ for the wave function expansion inside the atomic spheres is confined to ℓ max = 10. The core cutoff energy is -81.66 eV and the plane wave cutoff, Kmax = 8/Rmt (Rmt is the smallest muffin-tin radius in the unit cell) is chosen for the expansion of wave functions in the interstitial region. The charge density is Fourier expanded up to Gmax = 12. The Rmt values for TaRu are chosen to be 2.2 a.u. for both Ta and Ru.3. Results and Discussion
- In this section we present the structural, electronic and elastic properties of TaRu binary alloys using GGA and LDA exchange-correlation potentials.
3.1. Structural Properties and Phase Transformations
- Tantalum-Ruthenium crystal has a CsCl-structure (β-phase) with a space group
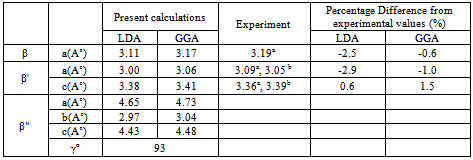
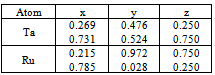
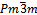 where Ta and Ru atoms are occupying the corners and the center of the cube. This material transforms martensitically from the parent phase (β) to a monoclinic martensitic phase (β") with an intermediate tetragonal phase (β') at 1100oC[3-8]. From Table 1, one can see that the calculated lattice constants agree well with the experimental values[8]. In order to obtain the crystal structure of the β′ phase, we deformed the CsCl-type structure of the β phase by continuously varying the c/a ratio, and keeping the volume fixed at its optimal value. In Fig.1 we present the relation of energy change versus the c/a ratio, where one can find two local minima at 0.94 (0.94) and 1.12 (1.13) using GGA (LDA) exchange-correlation potentials. The local minima at 1.12 (1.13) are lower in energy than the 0.94 minimum. This means that the cubic phase is unfavorable in energy as compared to the tetragonal phase, and undergoes two continuous tetragonal transformations. The β phase first undergoes cubic to tetragonal transformations with c/a =0.94, and then with c/a =1.12 (1.13). Our results show that the optimal c/a for the β′ phase is 1.12 (1.13), which is very close to the experimental value 1.09[5] and 1.12[10]. There is another transformation near 800ºC that has been evidenced experimentally[7-9, 17], where the structure transforms to monoclinic (β" phase). The optimum volume of β" phase is found to be the same as the other two phases (β, β'). In addition to volume optimization, we optimized c/a and b/a ratios at constant volumes of 32 (30) ų for GGA (LDA) exchange-correlation potentials, see Fig 2. Moreover, we optimized the γ angle for the β" phase, which is found to be 93° as can be seen in Fig.3. The final stage in building β" phase is by allowing the atoms to locate themselves in positions with minimum forces, i.e. finding the equilibrium positions of all individual atoms using a damped Newton dynamics method. In Table 2, we display the atomic positions for β" phase after relaxation.Furthermore, we performed geometrical optimization and a similar symmetry analysis to determine the crystal structure of the β′ and β" phases. It is found that the β′ phase has the P4/mmm space group with atomic positions: Ta (0, 0, 0), Ru (0.5, 0.5, 0.5) and β" has the P21/m space group with atomic position present in Table 2. The detailed lattice constants of the β′ and β" phases are listed in Table 1, the calculated volume of three phases is about 32 Å3, and thus, the martensitic transformation involves almost no change in volume. This indicates that TaRu is a shape memory alloy, since volume conservation is a necessary and sufficient condition for the shape memory effect in transforming the system from a martensitic to cubic austenitic phase[18].
where Ta and Ru atoms are occupying the corners and the center of the cube. This material transforms martensitically from the parent phase (β) to a monoclinic martensitic phase (β") with an intermediate tetragonal phase (β') at 1100oC[3-8]. From Table 1, one can see that the calculated lattice constants agree well with the experimental values[8]. In order to obtain the crystal structure of the β′ phase, we deformed the CsCl-type structure of the β phase by continuously varying the c/a ratio, and keeping the volume fixed at its optimal value. In Fig.1 we present the relation of energy change versus the c/a ratio, where one can find two local minima at 0.94 (0.94) and 1.12 (1.13) using GGA (LDA) exchange-correlation potentials. The local minima at 1.12 (1.13) are lower in energy than the 0.94 minimum. This means that the cubic phase is unfavorable in energy as compared to the tetragonal phase, and undergoes two continuous tetragonal transformations. The β phase first undergoes cubic to tetragonal transformations with c/a =0.94, and then with c/a =1.12 (1.13). Our results show that the optimal c/a for the β′ phase is 1.12 (1.13), which is very close to the experimental value 1.09[5] and 1.12[10]. There is another transformation near 800ºC that has been evidenced experimentally[7-9, 17], where the structure transforms to monoclinic (β" phase). The optimum volume of β" phase is found to be the same as the other two phases (β, β'). In addition to volume optimization, we optimized c/a and b/a ratios at constant volumes of 32 (30) ų for GGA (LDA) exchange-correlation potentials, see Fig 2. Moreover, we optimized the γ angle for the β" phase, which is found to be 93° as can be seen in Fig.3. The final stage in building β" phase is by allowing the atoms to locate themselves in positions with minimum forces, i.e. finding the equilibrium positions of all individual atoms using a damped Newton dynamics method. In Table 2, we display the atomic positions for β" phase after relaxation.Furthermore, we performed geometrical optimization and a similar symmetry analysis to determine the crystal structure of the β′ and β" phases. It is found that the β′ phase has the P4/mmm space group with atomic positions: Ta (0, 0, 0), Ru (0.5, 0.5, 0.5) and β" has the P21/m space group with atomic position present in Table 2. The detailed lattice constants of the β′ and β" phases are listed in Table 1, the calculated volume of three phases is about 32 Å3, and thus, the martensitic transformation involves almost no change in volume. This indicates that TaRu is a shape memory alloy, since volume conservation is a necessary and sufficient condition for the shape memory effect in transforming the system from a martensitic to cubic austenitic phase[18].
|
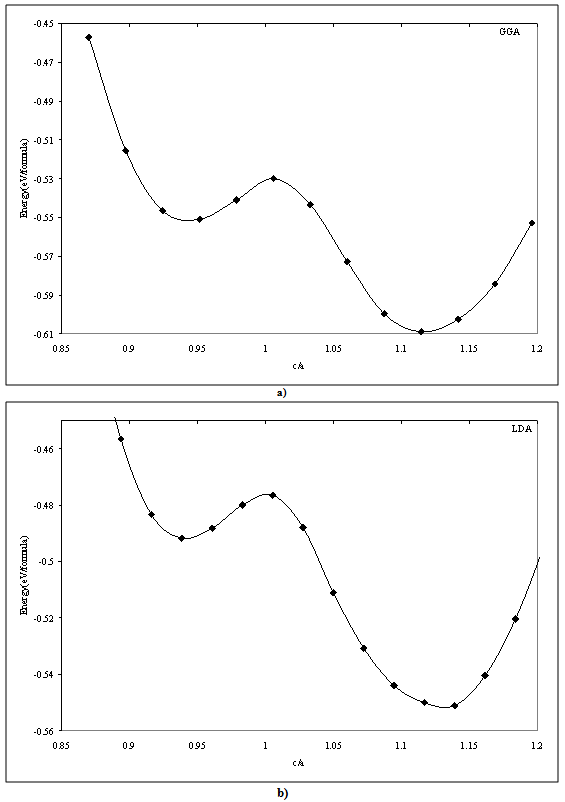 | Figure 1. Total energy of β' phase as a function of c/a at optimal volume; GGA (a), LDA (b) |
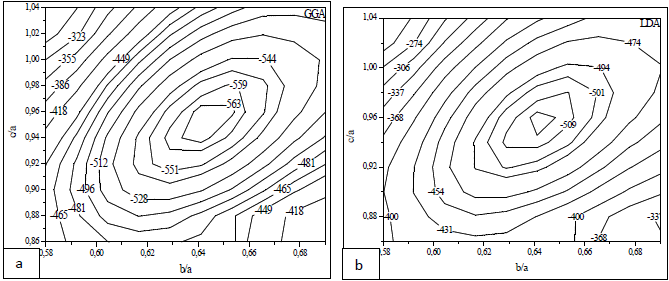 | Figure 2. Total energy as a function of b/a and c/a for β"-phase; GGA (a), LDA (b) |
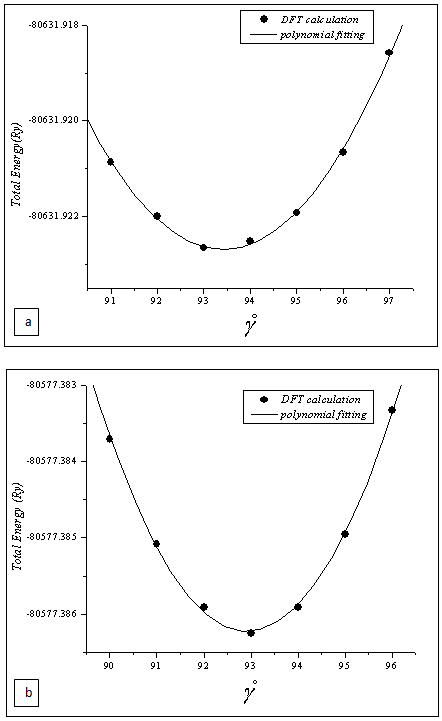 | Figure 3. Total energy as a function of γ; GGA (a), LDA (b) |
|
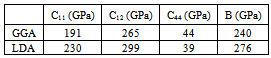
3.2. Elastic Properties
- The elastic properties play a key role in providing valuable information about structural stability and the binding characteristics between adjacent atomic planes. In general, there are only three independent elastic constants, C11, C12 and C44 for cubic crystals. To save the computation time, we have chosen three highly symmetrical types of deformation. The first type involves calculating the bulk modulus, which can be computed by the Birch-Murnaghan EOS[11]:
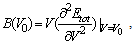 | (1) |
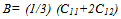 | (2) |
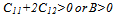 | (3-a) |
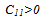 | (3-b) |
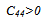 | (3-c) |
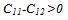 | (3-d) |
|
3.3. Energetic Properties
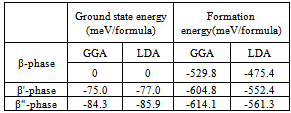
- We also calculated the formation energies for different structures by subtracting the weighted sum of the total energies of the constituent elements (Ta in fcc structure and Ru in hcp structure) from the total energy of the compound as[23]:
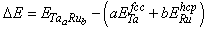 | (4) |
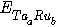 is the total energy of the compound per formula unit. The ground state is calculated relative to the β-phase, see Table 4. By comparing the formation energies of the three phases, we find that the β"-phase is the ground state with the lowest formation energy.
is the total energy of the compound per formula unit. The ground state is calculated relative to the β-phase, see Table 4. By comparing the formation energies of the three phases, we find that the β"-phase is the ground state with the lowest formation energy.
|
3.4. Electronic Properties
- To better examine the differences in the studied crystal structures, we plot the density of states (DOS) for β-phase, β'-phase and β"-phase in Fig.4. From this figure we note that the peaks of the β"-phase are the broadest among the three phases followed by the peaks of the β'-phase and then the β-phase. This can be ascribed to the fact that the β"-phase has a lowest symmetry as compared to β'-phase and finally β-phase. One can notice as well that total β"-phase has the lowest DOS at the Fermi level EF followed by that of β'-phase and finally that of β-phase. This could be used as an indication that the β"-phase is the most stable one[21]. Our calculations agree well with previous experimental results[3-6]. From this figure one can also notice that the total DOS below EF are mainly dominated by the Ru-d state, while the DOS above EF are mainly the Ta-d state. We find that the difference between Ru-d DOS and Ta-d DOS in β"-phase is very small as compared to the other two phases, so that the hybridization between Ta-d state and Ru-d state in β"-phase is the strongest among the three phases. In contrast, β-phase has the weakest hybridization.
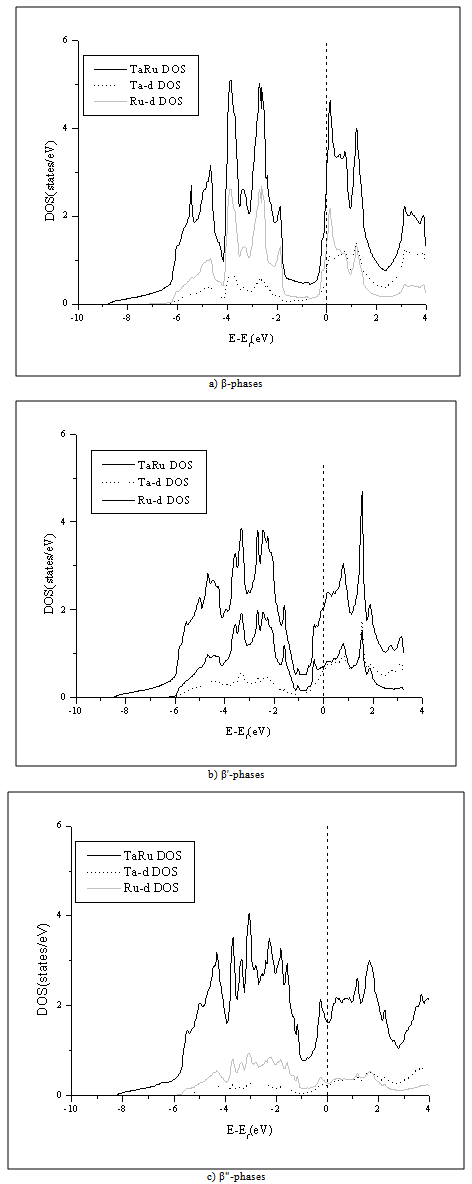 | Figure 4. Total and partial DOS for β (a), β' (b) and β"-phases(c) |
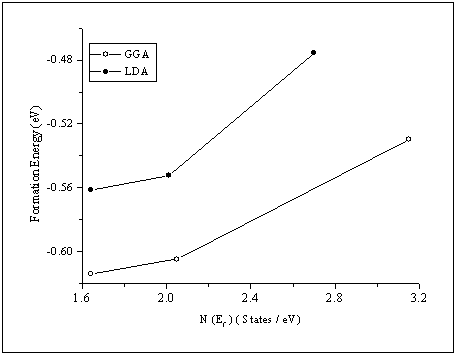 | Figure 5. Total DOS at Ef versus the formation energy for β, β' and β"-phases |
4. Conclusions
- The main conclusions of this work can be summarized as follows: 1. we put in evidence that the low-temperature ground-state structure is the β"-phase, which is found to be more stable than the tetragonal β'-phase and the cubic β-phase. 2. Our calculations show that the β"-phase has a monoclinic structure of (P21/m) symmetry.3. The calculated DOS shows that the hybridization between Ta “d” and Ru “d” states is responsible for the phase stability of TaRu.4. Our GGA calculations are found to be in a better agreement with the available experimental values[8, 10] than LDA.5. The Born’s mechanical stability condition, C11−C12 > 0, is not satisfied for β-phase due to the instability of this phase at low temperatures.
ACKNOWLEDGEMENTS
- The author thanks the staff at the theoretical physics laboratory of the University of Jordan.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML