-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Condensed Matter Physics
p-ISSN: 2163-1115 e-ISSN: 2163-1123
2012; 2(5): 126-134
doi:10.5923/j.ajcmp.20120205.04
Structural and Electronic Properties Calculations of AlAs1-xPx Alloy
Ali BENTOUAF, Mohammed AMERI, Rezki MEBSOUT, Djelloul HACHEMANE
Département de Physique, Faculté des Sciences, Université Djillali LIABES, Sidi-Bel, Abbès, 22000, Algérie
Correspondence to: Ali BENTOUAF, Département de Physique, Faculté des Sciences, Université Djillali LIABES, Sidi-Bel, Abbès, 22000, Algérie.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
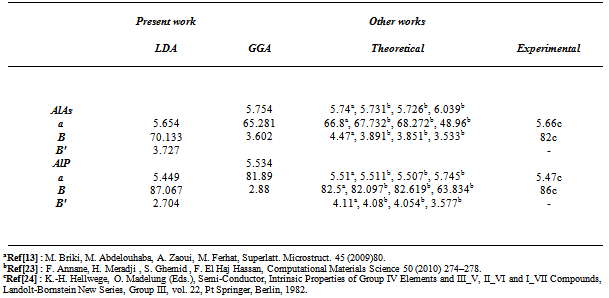
Based on the self-consistent ab initio the full-potential linear muffin-tin orbital (FP-LMTO) method, the structural, electronic, optical, and thermodynamic properties of AlAs1-xPx ternary semiconductor alloys have been investigated. The exchange–correlation potential was calculated using both the local density approximation (LDA) and generalized gradient approximation (GGA). The ground-state properties are determined for the cubic bulk materials AlAs, AlP, and their mixed crystals at various concentrations (x = 0.25, 0.5, and 0.75). Deviation of the lattice parameter from Vegard’s law and the bulk modulus from linear concentration dependence has been examined. The microscopic origins of the band-gap bowing parameter have been discussed. Moreover, the refractive index for AlAs1-xPx is studied using Reedy and Nazeer model. Besides, the thermodynamic stability of the alloys of interest is investigated by means of the miscibility critical temperature.
Keywords: FP-LMTO, Electronic Properties, Optical Properties, AlAs1-xPx Alloy
Cite this paper: Ali BENTOUAF, Mohammed AMERI, Rezki MEBSOUT, D, Structural and Electronic Properties Calculations of AlAs1-xPx Alloy, American Journal of Condensed Matter Physics, Vol. 2 No. 5, 2012, pp. 126-134. doi: 10.5923/j.ajcmp.20120205.04.
Article Outline
1. Introduction
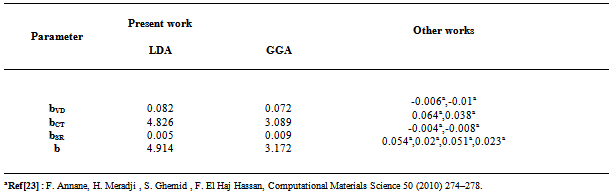
- Recently, III–V zinc blende semiconductors compounds have become an area of great technological activity. The reason for this is the possibility of producing novel materials with adjustable electronic and magnetic properties. Among them, the aluminum compounds AlAs and AlP are concerned in this paper. AlAs is one of the most important electronic and optoelectronic materials because of its frequent incorporation into GaAs-based heterostructures [1,2]. AlP, with the largest direct gap of the III–V compound semiconductors, is undoubtedly the most ‘‘exotic’’ and least studied[1]. However, in recent years, it is attracted special attention to its incorporation in the AlAs/AlP and GaP/AlP - based heterostructures. AlAs/AlP superlattices are attractive due to their potential applications in optoelectronic devices because they are expected to become direct band gap materials[3].GaP/AlP-based heterostructures are attractive in their characteristics for the development of optoelectronic devices operating in the yellow-green spectral region[4,5] and are considered as an alternative to a GaN/AlGaN system for the development of infrared semiconductor lasers and detectors [6]. Although there have been numerous calculations[7–9] of the structural, electronic and optical properties of aluminum compounds using different methods, to our knowledge there are few reports that had used the full potential calculation FP-LAPW to calculate the electronic, structural and optical properties for those compounds. Khanin and Kulkova[10] and Reshak and Auluck[11] used FP-LAPW method within local density approximation (LDA)[12] of the exchange – correlation energy to calculate the electronic and optical properties respectively. Recently, Briki et al.[13] studied the effects of relativistic on the structural and transport properties of III–V compounds utilizing LDA andPBE-GGA[14] for the exchange– correlation energy.In the present work, we have aimed to combine AlP and AlAs compounds having different structural and electronic properties in order to obtain new materials, AlAs1-xPx ternary alloys with intermediate properties. However, to the best of our knowledge, no experimental or theoretical investigations of AlAs1-xPx alloys have been appeared in the literature. The present work study the structural, electronic, optical, and thermodynamic properties of these alloys by using a full-potential, linear muffin-tin-orbital (FP-LMTO) method. The physical origins of gap bowing are calculated following the approach of Zunger and co-workers[15].A brief description of the computational details and methodology are given in Section 2. We present the theoretical results and discussion concerning the structural, electronic, optical and thermodynamic properties in Section 3. The conclusion is given in Section 4.
2. Computational Details
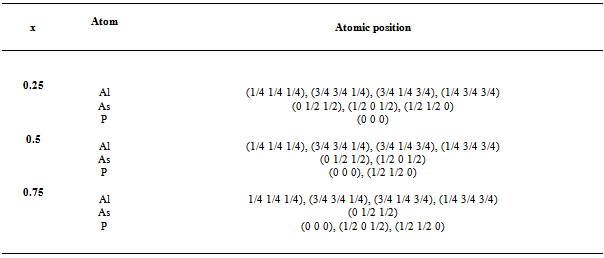
- The calculations reported here were carried out using the ab-initio full-potential linear muffin-tin orbital (FP- LMTO) method as implemented in the Lmtart code[16-18]. The exchange and correlation potential was calculated using the local density approximation (LDA)[19] and the generalized approximation (GGA)[20]. This is an improved method compared to previous (LMTO) methods. The FP-LMTO method treats muffin-tin spheres and interstitial regions on the same footing, leading to improvements in the precision of the eingen-values. At the same time, the FP-LMTO method, in which the space is divided into an interstitial regions (IR) and non overlapping muffin-tin spheres (MTS) surrounding the atomic sites, uses a more complete basis than its predecessors. In the IR regions, the basis functions are represented by Fourier series. Inside the MTS spheres, the basis functions are represented in terms of numerical solutions of the radial Schrödinger equation for the spherical part of the potential multiplied by spherical harmonics. The charge density and the potential are represented inside the MTS by spherical harmonics up to lmax = 6. The integrals over the Brillouin zone are performed up to 55 special k-points for binary com-pounds and 27 special k-points for the alloys in the irreducible Brillouin zone (IBZ), using the Blöchl’s modified tetrahedron method[21]. The self - consistent calculations are considered to be converged when the total energy of the system is stable within 10–5 Ry. In order to avoid the overlap of atomic spheres the MTS radius for each atomic position is taken to be different for each case. Both the plane waves cut-off are varied to ensure the total energy convergence. The values of the sphere radii (MTS), number of plane waves (NPLW).
3. Results and Discussions
3.1. Structural Parameters
|
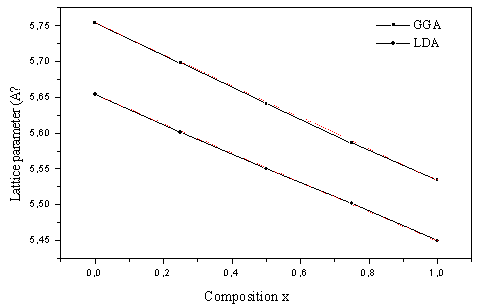 | Figure 1. Composition dependence of the calculated lattice constants (solid squares) of GGA and (solid circle) of LDA of AlAs1-xPx alloy compared with Vegard’s prediction (dot line) |
|
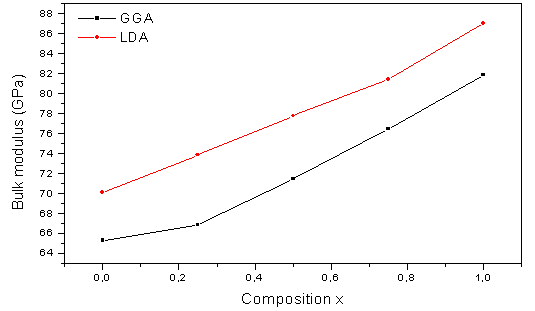 | Figure 2. Composition dependence of the calculated bulk modulus (red solid) of LDA and (black solid) of GGA of AlAs1-xPx alloy |
3.2. Electronic Properties
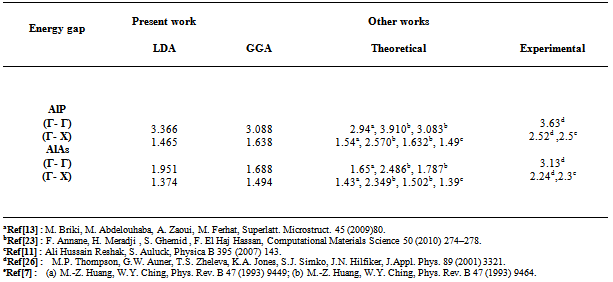
- The self consistent scalar relativistic band gaps of the compounds under investigation and their alloys were calculated within LDA and GGA schemes. An indirect band gap (Г –X) has been observed for AlAs and AlP compounds. The results are presented in Table 3. The values obtained for the band gap within GGA are in better agreement with available experimental results in comparison with the values calculated by LDA. In fact, it is well known that the LDA usually underestimates the energy gap[27]. It is noticeable that the GGA scheme, which is based on potential optimization, is capable of giving a more reliable band structure. The calculated energy gaps for AlAs1-xPx alloys are presented in Table 4. In Fig. 3, we display the composition dependence of the calculated band gaps using LDA and GGA schemes. The results are shown in Fig. 3 and obey the following variations:
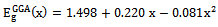 | (1) |
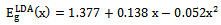 | (2) |
|
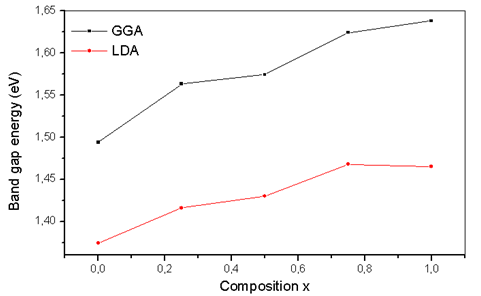 | Figure 3. Variation of the calculated band gap versus x concentration of AlAs1-xPx alloys using both GGA and LDA exchange and correlation potentials |
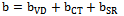 | (3) |
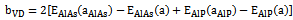 | (4) |
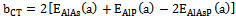 | (5) |
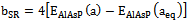 | (6) |
|
3.3. Linear Optical Properties
- It is well known that the basic optical properties of semiconductors result from the electronic excitation in crystals when an electromagnetic wave is incident on them. The calculation of the optical properties of the solids is beset with numerous problems. The knowledge of the dielectric functions
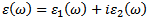 allows to describe the optical properties of the medium at all phonon energies. Calculations of the dielectric function involve the energy eigen-values and the electron wave functions. These are the natural output of the ab initio band structure calculation which is usually performed under LDA and GGA[30,31] .We have calculated the frequency dependent imaginary dielectric function and real dielectric function. The effects of using K points in the BZ have already been discussed in the earlier work by Khan et al (1993)[32]. The knowledge of both the real and the imaginary parts of the dielectric function allows the calculation of important optical functions. In this paper, we also present and analyze the refractive index
allows to describe the optical properties of the medium at all phonon energies. Calculations of the dielectric function involve the energy eigen-values and the electron wave functions. These are the natural output of the ab initio band structure calculation which is usually performed under LDA and GGA[30,31] .We have calculated the frequency dependent imaginary dielectric function and real dielectric function. The effects of using K points in the BZ have already been discussed in the earlier work by Khan et al (1993)[32]. The knowledge of both the real and the imaginary parts of the dielectric function allows the calculation of important optical functions. In this paper, we also present and analyze the refractive index 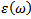 given by:
given by: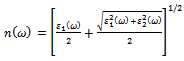 | (7) |
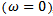 , we obtain the following relation:
, we obtain the following relation: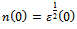 | (8) |
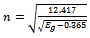 | (9) |
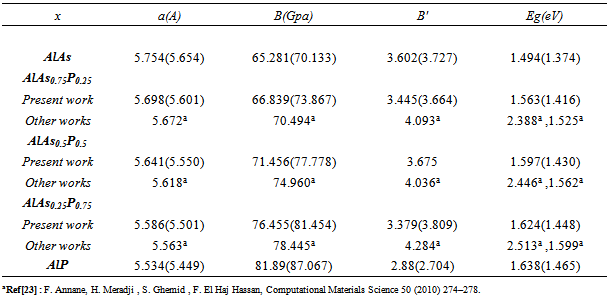
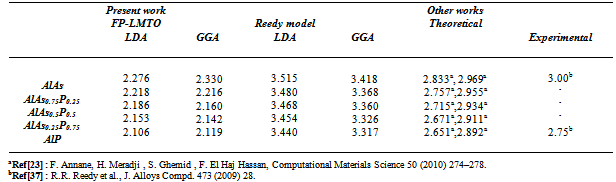
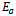 is the energy gap in eV. This equation is a straightforward modification of the original Moss equation[34], with a second arbitrary constant (0.365) added in order to improve the results obtained.In Table 6, we summarize the calculated values of the refractive index for the alloy under investigation, obtained by using the FP-LMTO method and Reddy et al. model. Comparison with the available data has been made where possible. It is clear that the values of the refractive index obtained by the FP-LMTO occur within the range of those obtained using Reddy et al. model; and for the end-point compounds (i.e. AlAs and AlP) are in good agreement with available experimental results.Fig. 4 shows the variation of the calculated refractive index versus concentration for the alloys. One can notice that the refractive index decreases monotonically with increasing P content over the entire range of 0–1 for both FP-LMTO and model used. The calculated refractive index versus concentration is fitted by a polynomial equation. The results are summarized as follows:
is the energy gap in eV. This equation is a straightforward modification of the original Moss equation[34], with a second arbitrary constant (0.365) added in order to improve the results obtained.In Table 6, we summarize the calculated values of the refractive index for the alloy under investigation, obtained by using the FP-LMTO method and Reddy et al. model. Comparison with the available data has been made where possible. It is clear that the values of the refractive index obtained by the FP-LMTO occur within the range of those obtained using Reddy et al. model; and for the end-point compounds (i.e. AlAs and AlP) are in good agreement with available experimental results.Fig. 4 shows the variation of the calculated refractive index versus concentration for the alloys. One can notice that the refractive index decreases monotonically with increasing P content over the entire range of 0–1 for both FP-LMTO and model used. The calculated refractive index versus concentration is fitted by a polynomial equation. The results are summarized as follows: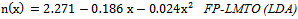 | (10) |
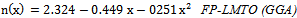 | (11) |
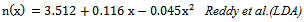 | (12) |
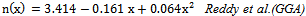 | (13) |
|
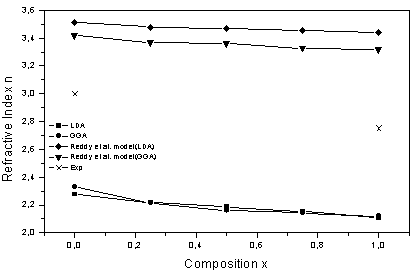 | Figure 4. Variation of the calculated refractive index versus x concentration of AlAs1-xPx alloys using both GGA and LDA exchange and correlation potentials |
3.4. Thermodynamic Properties
- In this section we present a rigorous theoretical study of the thermodynamic properties of AlAs1-xPx alloys, the calculations carried out here are based on ab initio method within GGA scheme. We calculate the Gibbs free energy of mixing ∆Gm (x, T) which allows us to access the T–x phase diagram and obtain the critical temperature, Tc, for miscibility. Details of the calculations are given in Refs.[39–41]. For alloys, Gibbs free energy of mixing ∆Gm is expressed as:
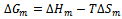 | (14) |
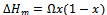 | (15) |
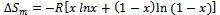 | (16) |
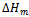 and
and 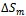 are the enthalpy and entropy of mixing, respectively;
are the enthalpy and entropy of mixing, respectively;  the interaction parameter and depends on material; R the gas constant and T the absolute temperature.Indeed, an importance contribution arises from the mixing enthalpy, which can be obtained from the calculated total energies as
the interaction parameter and depends on material; R the gas constant and T the absolute temperature.Indeed, an importance contribution arises from the mixing enthalpy, which can be obtained from the calculated total energies as 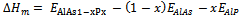 , where
, where 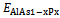 ,
, 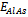 and
and 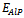 are the respective energies of AlAs1-xPx alloy, and the binary compounds AlAs and AlP. We then calculated
are the respective energies of AlAs1-xPx alloy, and the binary compounds AlAs and AlP. We then calculated 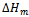 to obtain
to obtain 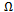 as a function of concentration. From a linear fit we obtained:
as a function of concentration. From a linear fit we obtained: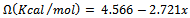 which shows the marginal dependence of
which shows the marginal dependence of 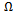 to the concentration x for AlAs1-xPx alloys.Now, we first calculate
to the concentration x for AlAs1-xPx alloys.Now, we first calculate 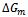 by using Eqs. (14)–(16). Then we use the Gibbs free energy at different concentrations to calculate the T–x phase diagram which shows the stable, metastable and unstable mixing regions of the alloy. At a temperature lower than the critical temperature Tc, the two binodal points are determined as those points at which the common tangent line touches the
by using Eqs. (14)–(16). Then we use the Gibbs free energy at different concentrations to calculate the T–x phase diagram which shows the stable, metastable and unstable mixing regions of the alloy. At a temperature lower than the critical temperature Tc, the two binodal points are determined as those points at which the common tangent line touches the 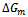 curves. The two spinodal points are determined as those points at which the second derivative of
curves. The two spinodal points are determined as those points at which the second derivative of 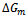 is zero;
is zero; 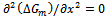 .
.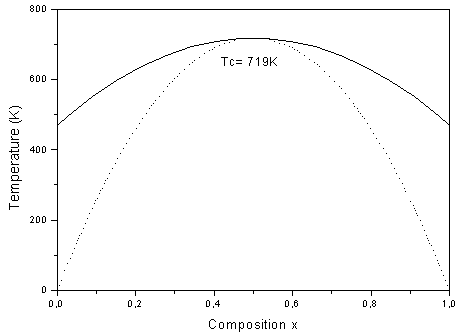 | Figure 5. T–x phase diagram for AlAs1-xPx alloys. Dotted line: binodal curve; solid line: spinodal curve |
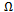 , hence the phase diagram looks symmetric. We observed a critical temperature Tc of 719K for AlAs1-xPx alloys. The spinodal curve in the phase diagram marks the equilibrium solubility limit, i.e. the miscibility gap. For temperatures and compositions above this curve a homogeneous alloy is predicted. The wide range between spinodal and binodal curves indicates that the alloy may exist as a metastable phase. Hence our results indicate that the AlAs1-xPx alloys are stable at relatively high temperature.
, hence the phase diagram looks symmetric. We observed a critical temperature Tc of 719K for AlAs1-xPx alloys. The spinodal curve in the phase diagram marks the equilibrium solubility limit, i.e. the miscibility gap. For temperatures and compositions above this curve a homogeneous alloy is predicted. The wide range between spinodal and binodal curves indicates that the alloy may exist as a metastable phase. Hence our results indicate that the AlAs1-xPx alloys are stable at relatively high temperature.4. Conclusions
- In this paper, the structural, electronic, optical and thermodynamic properties of the zinc blend AlAs1-xPx ternary alloys as a function of the composition x are presented using density-functional theory within different approximations of exchange-correlation energy: LDA and GGA. A nonlinear behavior of the lattice constant, bulk modulus and band gap dependence on x has been observed. Our results are in favorable agreement with the previous theoretical works. The bowing is found to be mainly caused by the charge transfer effect, while the volume deformation and the structural relaxation contribute to the bowing parameter at smaller magnitude.We find that n(Eg) for AlAs1-xPx alloys increases with decreasing energy gap, in agreement with the quantum- mechanics equation. The investigation of the thermodynamic stability allowed us to calculate the critical temperature which is 719K.
References
| [1] | I. Vurgaftman, J.R. Meyer, L.R. Ram-Mohan, J. Appl. Phys. 89 (2001) 5815. |
| [2] | S. Adachi, GaAs and Related Materials: BulkSemiconducting and Superlattice Properties, World Scientific, Singapore, 1994. |
| [3] | T. Ohnuma, M. Nagano, Jpn. J. Appl. Phys. 39 (2000) L972. |
| [4] | A. Morii, H. Okagawa, K. Hara, et al., Electron. Lett. 28 (1992) 836. |
| [5] | R.K. Soni, S. Tripathy, H. Asahi, Physica E 21 (2004) 131. |
| [6] | M.P. Semtsiv, U. Müller, W.T. Masselink, et al., Appl. Phys. Lett. 89 (2006) 84102. |
| [7] | (a) M.-Z. Huang, W.Y. Ching, Phys. Rev. B 47 (1993) 9449; (b) M.-Z. Huang, W.Y. Ching, Phys. Rev. B 47 (1993) 9464. |
| [8] | A.R. Jivani, H.J. Trivedi, P.N. Gajjar, A.R. Jani, Pramana J. Phys. 64 (1) (2005) 153. |
| [9] | S.Zh. Karaahanov, L.C. Yan Voon, Semiconductors 39 (2) (2005) 161. |
| [10] | D.V. Khanin, S.E. Kulkova, Russ. Phys. J. 48 (1) (2005) 70. |
| [11] | Ali Hussain Reshak, S. Auluck, Physica B 395 (2007) 143. |
| [12] | J.P. Perdew, Y. Wang, Phys. Rev. B 45 (1992) 13244. |
| [13] | M. Briki, M. Abdelouhaba, A. Zaoui, M. Ferhat, Superlatt. Microstruct. 45 (2009) 80. |
| [14] | J.P. Perdew, S. Burke, M. Ernzerhof, Phys. Rev. Lett. 77 (1996) 3865. |
| [15] | (a) G.P. Srivastava, G.L. Martins, A. Zunger, Phys. Rev. B 31 (1985) 2561; (b) J.E. Bernard, A. Zunger, Phys. Rev. B 34 (1986) 5992. |
| [16] | S. Y. Savrasov, Phys. Rev. B 54 , (1996) 16470 |
| [17] | S. Savrasov, D. Savrasov, Phys. Rev. B 46 ( 1992) 12181 |
| [18] | D. Rached, M. Rabah, N. Benkhettou, M. Driz and B. Soudini Physica B : Physics of Condensed Matter, 337/1-4 (2003) pp. 394-403 |
| [19] | J.P. Perdew, Y. Wang, Phys. Rev. B 45 (1992) 13244. |
| [20] | J.P. Perdew, S. Burke, M. Ernzerhof, Phys. Rev. Lett. 77 (1996) 3865 |
| [21] | P. Blochl, O. Jepsen, and O. K. Andersen, Phys. Rev. B 49, 16223 (1994). |
| [22] | F.D. Murnaghan, Proc. Nat. Acad. Sci. USA 30 (1944) 5390. |
| [23] | F. Annane, H. Meradji , S. Ghemid , F. El Haj Hassan, Computational Materials Science 50 (2010) 274–278. |
| [24] | K.-H. Hellwege, O. Madelung (Eds.), Semi-Conductor, Intrinsic Properties of Group IV Elements and III_V, II_VI and I_VII Compounds, Landolt-Bornstein New Series, Group III, vol. 22, Pt Springer, Berlin, 1982 |
| [25] | L. Vegard, Z. Phys. 5 (1921) 17. |
| [26] | M.P. Thompson, G.W. Auner, T.S. Zheleva, K.A. Jones, S.J. Simko, J.N. Hilfiker, J.Appl. Phys. 89 (2001) 3321. |
| [27] | P. Dufek, P. Blaha, K. Schwarz, Phys. Rev. B 50 (1994) 7279. |
| [28] | F. El Haj Hassan, H. Akbarzadeh, Mater. Sci. Eng. B 121 (2005) 170. |
| [29] | W. Sargent, Table of Periodic Properties of the Elements, Sargent-Welch Scientific, Skokie, IL, 1980. |
| [30] | Alouani M, Koch J M and Khan M A J. Phys. F16 (1986) 437 |
| [31] | Koenig C and Khan M A Phys. Rev. B17 (1983) 6129 |
| [32] | Khan M A, Kashyap A, Solanki A K, Nautiyal T and Auluck S Phys. Rev. B48 (1993)16947 |
| [33] | Y. Al Douri, H. Abid, H. Aourag, Mater. Chem. Phys. 65 (2000) 117. |
| [34] | T.S. Moss, Phys. Status Solidi (b) 131 (1985) 415. |
| [35] | N.M. Ravindra, S. Anuch, V.K. Srinvastava, Phys. State Solid (b) 93 (1979) 115. |
| [36] | R. Reddy, Y. Nazeer Ahammed, Infra. Phys. Technol. 36 (1995) 825. |
| [37] | R.R. Reedy et al., J. Alloys Compd. 473 (2009) 28. |
| [38] | M. Anani, C. Mathieu, S. Lebida, Y. Amar, Z. Chama, H. Abid, Comput. Mater. Sci. 41 (2008) 570. |
| [39] | R.A. Swalin, Thermodynamics of Solids, Wiley, New York, 1961. |
| [40] | L.G. Ferreira, S.H. Wei, J.E. Bernard, A. Zunger Phys. Rev. B 40 (1989) 3197. |
| [41] | L.K. Teles, J. Furthmüller, L.M.R. Scolfaro, J.R. Leite, F. Bechstedt, Phys. Rev. B 62(2000) 2475 |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML