P. Koteeswari 1, S. Suresh 2, P. Mani 1
1Department of Physics, Hindustan Institute of Technology, Padur, India
2Department of Physics, Loyola College, Chennai, 600 025, India
Correspondence to: S. Suresh , Department of Physics, Loyola College, Chennai, 600 025, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Single crystals of non-linear optical material, L-Serine Sodium Nitrate (LSSN) have been grown by slow evaporation technique. The crystal system and lattice parameters were found from single crystal X-ray diffraction. Some fundamental data such as valance electron plasma energy, Penn gap, Fermi energy and electronic polarizability of the grown crystal were calculated. Microhardness investigations are conducted on the grown crystals. Mechanical behaviour was analyzed using Vicker’s microhardness test. Microhardness studies revealed that the hardness of the grown crystal decrease with an increase in load. Meyer’s index number n was calculated and found that the material belongs to hard material category .The dielectric constant measurements are carried out and the nature of variation of dielectric constant and dielectric loss in the frequency range of 50 Hz to 5 MHz is studied and reported.
Keywords:
Single Crystal, Growth from Solution, Single X-Ray Diffraction, Microhardness, Dielectric Constant
Cite this paper:
P. Koteeswari , S. Suresh , P. Mani , "Synthesis, Theoretical, Mechanical and Dielectric Property of L-Serine Sodium Nitrate NLO Single Crystal", American Journal of Condensed Matter Physics, Vol. 2 No. 5, 2012, pp. 116-119. doi: 10.5923/j.ajcmp.20120205.02.
1. Introduction
In recent years, great efforts have been made to develop new organic, inorganic and semi-organic nonlinear optical (NLO) crystals due to their widespread applications such as frequency conversion, high-speed information processing, optical communications, and optical data storage[1-3]. In the field of nonlinear optical crystal growth, amino acids play a vital role. Amino acids exhibit natural chiral properties and crystallize in the non-centrosymmetric space groups, which is an essential criterion for NLO applications. In addition, amino acids possess particular features, such as weak Vander Waals and hydrogen bonds, wide transparency range in the visible region and zwitter ionic nature of the molecules. Complexes of amino acids with inorganic salts are promising materials for optical second harmonic generation (SHG) as they tend to combine the advantages of organic amino acid and inorganic salt. In the present work, L-Serine Sodium Nitrate was synthesized and the crystals were grown by slow evaporation technique. The grown crystals were characterized by Single X-ray diffraction, microhardness and dielectric studies. Fundamental parameters like plasma energy, Penn gap, Fermi energy and electronic polarizability of the crystal were calculated for the First time.
2. Crystal Growth
Single crystals of L-Serine Sodium Nitrate were grown from L-serine and sodium nitrate taken in equimolar ratio in aqueous solution by slow evaporation method. The solution was stirred continuously using a magnetic stirrer. The prepared solution was filtered and kept undisturbed at room temperature. Tiny seed crystals with good transparency were obtained due to the spontaneous nucleation. Among them, defect free seed crystal was suspended in the mother solution, which was allowed to evaporate at room temperature. Large size single crystals were obtained due to collection of monomers at the seed crystal sites from the mother solution after the nucleation process was completed. Figure 1 shows as-grown crystals of LSSN. | Figure 1. Photograph of as grown crystal of LSSN |
3. Results and Discussion
3.1. Single Crystal X-Ray Diffraction and Fundamental Parameters
Single crystal X-ray diffraction analysis for the grown crystals has been carried out to identify the cell parameters using an ENRAF NONIUS CAD4 automatic X-ray diffractometer. Calculated lattice parameters are: a = 5.63Å, b = 8.59Å, c = 9.37Å, α = β = γ = 90o and the crystals belongs to orthorhombic system with space group is P21P21P21. These values are found to agree with the reported values[4]. The molecular weight of the grown crystal is M=190.08 g, and total number of valence electron Z=66. The density of the grown crystal was found to be ρ=1.50 g/cm3 and dielectric constant at 1 MHz is 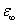 =18. The valence electron plasma energy,
=18. The valence electron plasma energy, 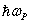 is given by
is given by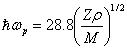 | (1) |
where Z is the total number of valence electrons, ρ is the density and M is the molecular weight of the LSSN single crystal. The Plasma energy is terms of Penn gap and Fermi energy[5] in eV is given as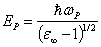 | (2) |
and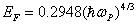 | (3) |
Polarizability, α is obtained using the relation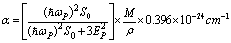 | (4) |
where S0 is a constant for a particular material, and is given by 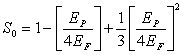 | (5) |
The value of α so obtained agrees well with that of Clausius-Mossotti equation, which is given by,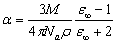 | (6) |
| Table 1. Some theoretical data for LSSN single crystal |
| | Parameters | Values | | Plasma energy (eV) | 20.78 | | Penn gab ( eV) | 5.04 | | Fermi gap (eV) | 16.67 | | Polarizability (cm3) Penn analysis | 1.594 x 10-23 | | Clausius-Mossotti Equation | 1.583 x 10-23 |
|
|
Where the symbols have their usual significance. Na is Avagadro number and the calculated fundamental data on the grown crystal of LSSN are listed in Table1.
3.2. Microhardness Studies
Mechanical strength of the materials plays a key role in device fabrication. It is a measure of the resistance, the lattice offers to local deformation[6]. Selected smooth and flat surface of the grown crystal was subjected to hardness study at room temperature with the load range 10–200 g using Vicker’s hardness tester (LEITZ WETZLER) fitted with a diamond pyramidal indenter and attached to a incident light microscope. The indentation time was kept as 5 s for all the loads. The Vicker’s hardness number was calculated using the relation,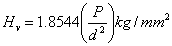 | (7) |
where P is the applied load in kg and d is the diagonal length of the indentation impression in mm. Variation of hardness value, Hv with the load P is shown in Figure 2. From the profile, it is observed that the hardness decreases with increase in load satisfying indentation size effect (ISE). Well-known Meyer’s law gives the relationship between load and size of the indentation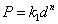 | (8) |
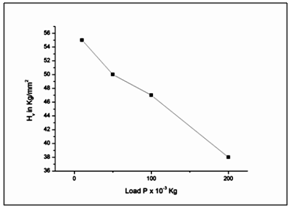 | Figure 2. Variation of hardness number (HV) with load P |
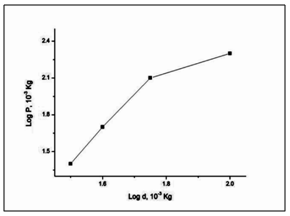 | Figure 3. Plot of log P vs log d |
where k1 and n are constants for a particular material. The work hardening coefficient was calculated from the plot of log P versus log d, depicted in Figure 3. Since the material takes some time to revert to the elastic mode after every indentation, a correction x, known as the measure of dislocation density of the material is applied to the d value and the Kick’s law is related as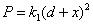 | (9) |
Simplifying, Eqs. (8) and (9) we have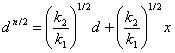 | (10) |
The slope of dn/2 versus d yields (k2/k1)1/2 and the intercept is a measure of x. The yield strength of the material[7] can be found out using the relation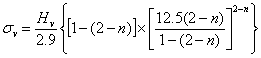 | (11) |
Using these relations, the hardness parameters of LSSN crystals such as, n, k1, k2, x and σv were calculated and presented in Table 2.The elastic stiffness constant (C11) were calculated for all the grown crystals using Wooster’s empirical relation as[8] 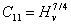 | (12) |
The calculated stiffness constant for a load from 10 gm to 200 gm has been calculated and is given in Tablle.3.| Table 2. The hardness parameters for the LSSN single crystal |
| | n | k1 106 (Kg/m) | k2 (Kg/m) | x(µm) | σv(MPa) | | 1.77 | 11.42 | 1.56 | 4 | 17.97 |
|
|
| Table 3. Stiffness constant of L-Serine Sodium Nitrate crystal |
| | Load P | d (mm) | Hv (Kg/mm2) | C11 x 1014 Pa | | 10 | 35 | 55 | 11.60 | | 50 | 40 | 50 | 9.40 | | 100 | 50 | 47 | 8.43 | | 200 | 100 | 38 | 5.81 |
|
|
3.3. Dielectric Studies
The dielectric constant and the dielectric loss of the LSSN crystals were studied at room temperature using HIOKI 3532 LCR HITESTER in the frequency region 50Hz-5MHz. Figure 4 shows the variation of dielectric constant (εr) with log frequency. From the plot, it is observed that the dielectric constant is relatively higher in the region from 50Hz-5MHz and further decreases with increase in frequency, and this trend continues up to 5 MHz After this, dielectric constant almost remains constant (εr=18) at all other higher frequencies. The high value of dielectric constant at low frequency is due to the presence of electronic, ionic, dipolar and space charge polarizations[9]. In accordance with Miller rule, the lower value of dielectric constant at higher frequencies is a suitable parameter for the enhancement of SHG coefficient[10]. The variation of dielectric loss with frequency is shown in Figure 5. The characteristic of low dielectric loss with high frequency for the sample suggests that the crystal possess enhanced optical quality with lesser defects and this parameter play a vital role for the fabrication of nonlinear optical devices[11].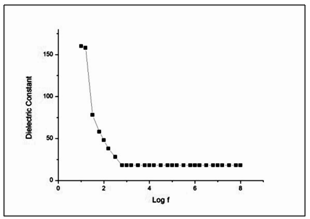 | Figure 4. Variation of dielectric constant with log f |
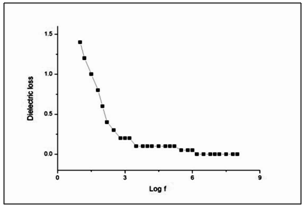 | Figure 5. Variation of dielectric loss with log f |
4. Conclusions
Good optical quality bulk single crystal of LSSN has been grown by slow evaporation technique. Single crystal XRD analysis confirms that the crystal belongs to orthorhombic system. Fundamental parameters like plasma energy, Penn gap, Fermi energy and electronic polarizability of the crystal have been calculated. From micro hardness test, it is observed that hardness number Hv decreases with the increase in load and the value of Meyer index number or the work hardening coefficient n was calculated as 1.77,which is less than 2 establishing that the crystal to be a hard material. The low value of work hardening coefficient shows less dislocation in the grown crystal since the dislocations present in the crystal cause work hardening coefficient. The frequency dependence of dielectric constant and dielectric loss is found to be decreased with increase in frequency at room temperature.
References
| [1] | T.Sasaki and A.Yokotani , J. Cryst. Growth. 99(1990) 820 |
| [2] | F.Tsunesada, T.Iwai, T.Watanabe, H.Adachi, M.Yoshimura, Y.Mori and T.Sasaki, J. Cryst. Growth. 2104 (2002) 237–239 |
| [3] | Y.Zhang, H.Li, B.Xi, Y.Che and J.Zheng, Mater. Chem. Phys. 108(2008)192 |
| [4] | S.D.Zulifiqar Ali Ahamed, G.R.Dillip, L.Manoj, B.Raghavaiah Deva Prasad Raju, Photonics Letters of Poland. 2(4) (2010)183-185 |
| [5] | Ravindra NM, Bharadwaj RP, Sunil Kumar K, and Srivastava VK, Infrared Phys. 21 (1981)369 |
| [6] | B.W.Mott, Microindentation Hardness Testing, Butterworth, London. (1956)206. |
| [7] | E.M.Onitsch, Mikroskopie. 2 (1947)131 |
| [8] | W.A.Wooster, Rep. Progr. Phys.16 (1953) 62 |
| [9] | J.S.Pan, X.W.Zhang, Acta Mat.54 (2006)1343. |
| [10] | U.Von Hundelshausen, Phys. Lett. 34A (1971) 7 |
| [11] | C.Balarew, R.Duhlew, J. Solid State Chem. 55(1984) 1 |


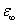 =18. The valence electron plasma energy,
=18. The valence electron plasma energy, 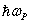 is given by
is given by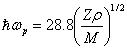
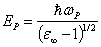
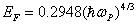
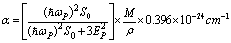
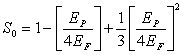
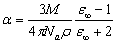
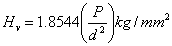
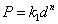


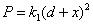
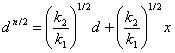
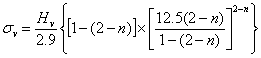
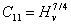


 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML