-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Condensed Matter Physics
p-ISSN: 2163-1115 e-ISSN: 2163-1123
2012; 2(4): 101-108
doi: 10.5923/j.ajcmp.20120204.05
Molecular Dynamics Simulations of Bottle-Brush Polymers with a Flexible Backbone under Theta and Good Solvent Conditions
Panagiotis E. Theodorakis 1, 2, Nikolaos G. Fytas 3
1Faculty of Physics,University of Vienna A-1090, Boltzmanngasse 5, Vienna, Austria
2Institute for Theoretical Physics and Center for Computational MaterialsScience (CMS), Technical University of Vienna A-1040 Vienna, Hauptstrasse8-10, Austria
3Departamento de Fisica Teorica I, Universidad Complutense de Madrid, Madrid, 28040, Spain
Correspondence to: Panagiotis E. Theodorakis , Faculty of Physics,University of Vienna A-1090, Boltzmanngasse 5, Vienna, Austria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Using molecular dynamics simulations of a standard bead-spring model for polymer chains,bottle-brush polymerswith a flexible backbone of Nbeffective units,where side chains of length N are grafted under theta and good solvent conditionsin the range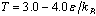 , are studied.The range of backbone and side chains' length varies correspondingly as
, are studied.The range of backbone and side chains' length varies correspondingly as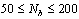 and
and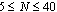 for two different grafting densities σ, namely σ=0.5 and 1.0.Even at temperatures T close to the theta point the side chains are significantly stretched, as it has been confirmed for bottle brushes with a rigid backbone, their linear dimension depending on the solvent quality only weakly. However, the distribution of monomers shows a more pronounced dependence, which we characterize through the asphericity and acylindricity as functions of σ, T, Nb, and N. In particular, increase of σ, T, Nb, and N increases the normalized asphericity and acylindricity of the macromolecule. Interestingly, we also find that the dimensions of the side chains reveals differences in the distributions of side chain monomers by changing the backbone length Nb as the region between the two backbone-ends increases. A method to extract the persistence length of bottle-brush macromolecules and its drawbacks is also discussed given that different measures of the persistence length are not mutually consistent with each other and depend distinctly both on Nb and the solvent quality.Macromolecules which consist of a backbone where side chains are graftedrandomly or regularly have recently found much interest[1-6]. Such macromolecules are described in terms of their structure by a multitudeof parameters, such as the backbone length Nb and the grafting densitythat the side chains with length N are grafted ontothe flexible backbone, while solvent conditions may also varyby variation of the temperature T or the pH of the solution resulting inthe structural change of these stimuli-responsive macromolecules.The response of the large scale structure of bottle-brush polymers tosolvent conditions is an intriguing We recall that for linear chains, the theta temperaturefor the present (implicit solvent) model has been roughlyestimated[46] as Ttheta≈ 3.0 (note, however, that there is still some uncertainty about the precise value of Ttheta,for a similar model[47] Ttheta= 3.18 in this case, couldonly be established for chain lengths exceeding N= 200).Thus, in the present work we have thoroughly studied thetemperature range
for two different grafting densities σ, namely σ=0.5 and 1.0.Even at temperatures T close to the theta point the side chains are significantly stretched, as it has been confirmed for bottle brushes with a rigid backbone, their linear dimension depending on the solvent quality only weakly. However, the distribution of monomers shows a more pronounced dependence, which we characterize through the asphericity and acylindricity as functions of σ, T, Nb, and N. In particular, increase of σ, T, Nb, and N increases the normalized asphericity and acylindricity of the macromolecule. Interestingly, we also find that the dimensions of the side chains reveals differences in the distributions of side chain monomers by changing the backbone length Nb as the region between the two backbone-ends increases. A method to extract the persistence length of bottle-brush macromolecules and its drawbacks is also discussed given that different measures of the persistence length are not mutually consistent with each other and depend distinctly both on Nb and the solvent quality.Macromolecules which consist of a backbone where side chains are graftedrandomly or regularly have recently found much interest[1-6]. Such macromolecules are described in terms of their structure by a multitudeof parameters, such as the backbone length Nb and the grafting densitythat the side chains with length N are grafted ontothe flexible backbone, while solvent conditions may also varyby variation of the temperature T or the pH of the solution resulting inthe structural change of these stimuli-responsive macromolecules.The response of the large scale structure of bottle-brush polymers tosolvent conditions is an intriguing We recall that for linear chains, the theta temperaturefor the present (implicit solvent) model has been roughlyestimated[46] as Ttheta≈ 3.0 (note, however, that there is still some uncertainty about the precise value of Ttheta,for a similar model[47] Ttheta= 3.18 in this case, couldonly be established for chain lengths exceeding N= 200).Thus, in the present work we have thoroughly studied thetemperature range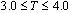 . From previous work[48] on rather long chains in polymer brushes on flat surfaces, using the same model[Eqs. (1) and (2)] to describe the interactions, it is known that for T= 4.0 one finds a behaviour characteristicfor (moderately) good solvents. Very good solvent conditionscould be obtained from a slightly different model that hasextensively been studied for standard polymer brushes[40,49],where the cut-off in Eq. (1) is chosen to coincide with theminimum of the potential,
. From previous work[48] on rather long chains in polymer brushes on flat surfaces, using the same model[Eqs. (1) and (2)] to describe the interactions, it is known that for T= 4.0 one finds a behaviour characteristicfor (moderately) good solvents. Very good solvent conditionscould be obtained from a slightly different model that hasextensively been studied for standard polymer brushes[40,49],where the cut-off in Eq. (1) is chosen to coincide with theminimum of the potential, 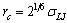 (and then also T= 1 can be chosen for this essentially a-thermal model).
(and then also T= 1 can be chosen for this essentially a-thermal model).
Keywords: Molecular Dynamics, Bottle-Brush Polymers, Structural Properties
Article Outline
1. Introduction
- Biopolymers with a related architecture are also abundant in nature;for example proteoglycans[8] or the aggrecan molecules kept responsible for the very good lubricating properties in human joints[9]. In thiscontext the change in the solvent conditions is an important parameter, and theinfluence of these parameters on bottle-brush polymers has beenstudiedfor the case of single[10-12] and two-component[12-14] bottle brushes with a rigid backbone,suggesting in agreement with theoretical predictions structures rangingfrom individual collapsed chains at low grafting densities to the so-called “pearl-necklace” structures for intermediate densities andto homogenous cylinders and Janus-like structures at even higher densities.Another interesting discussion regards the local "stiffness" traditionally measured by the persistence length lp and the effective contour length[15-18].It is argued that finding a unique persistencelength measuring the “intrinsic” stiffness of a polymer cannotbe defined in the standard fashion with definitions that would all agree for Gaussian chains. Therefore, it has recently been shown that the persistence length depends not onlyon the backbone length[19,20], but on the solvent conditions as well [15]. Although there exist many experimental and theoretical studies for the linear dimensions of these macromolecules in various solvents[3,4,19,21-36],there are very few systematic studies of this problem[15], wherethe power laws and the associated effective exponents have been discussed.It has been shown that for bottle brushes with a flexible backbone evenat the theta point the side chains are considerably stretched,their linear dimension depending on the solvent quality only weakly, whilethe dependence of the persistence length on backbone length and temperature has alsobeen discussed[15]. The present work intends to make a contribution in giving a geometrical intuitionof single-component bottle-brush polymers with a flexible backbone undertheta and good solvent conditions and how the distribution of monomers changesby changing the various parameters. A pertinent discussion for a method to compute the persistence lengthof these complex macromolecules and its drawbacks will be also presented.The rest of this paper is laid out as follows. In Section 2,the current simulation model and its analysis are unfolded. A relevantdiscussion for the peculiarities of our system of interest is also provided. Section 3 presents a brief discussion of properties and our numerical results.This manuscript closes in Section 4, with a short summary.
2. Model and Methods
- We describe the backbone chain and the side chains by a bead-spring model[37-43] where all beads interact with a truncated and shifted Lennard-Jones (LJ) potential ULJ(r) and nearest neighbours bonded together along a chain also experience the finitely extensible nonlinear elastic potential UFENE(r), r being the distance between the beads. Thus,
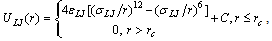 | (1) |
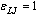 , σLJ = 1, the Boltzmann constant kB = 1, and in addition also the mass mLJ of beads is chosen to be unity. The potential of Eq. (1) acts between any pair of beads, irrespective of whether they are bonded or not. For bonded beads additionally the potential UFENE(r) is used,
, σLJ = 1, the Boltzmann constant kB = 1, and in addition also the mass mLJ of beads is chosen to be unity. The potential of Eq. (1) acts between any pair of beads, irrespective of whether they are bonded or not. For bonded beads additionally the potential UFENE(r) is used,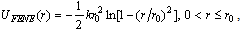 | (2) |
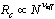 , is a delicate matter,νeff being an effective exponent and characterizes only the specifiedrange of rather small values of N and not the limit
, is a delicate matter,νeff being an effective exponent and characterizes only the specifiedrange of rather small values of N and not the limit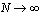 considered by most theories[6,25,33-35]. Thus, the actual value of νeff is generally of limited interest, it only gives an indication to whichpart of an extended crossover region the data belong. However,we emphasize that: (i) our range of N nicely corresponds tothe range available in experiments[1,2,21-23,32,46-48] and (ii) the analysis in term of power laws with effective exponents isa standard practice of experimentalists in this context.A simulation analysis for the static properties of bottle-brushmacromolecules with flexible backbone have been discussed in detail previously[15].In this work we rather focus on the overall shapes that suchmacromolecules obtain, and discuss various aspects that couldnot be discussed in the frame of effective exponent analysis.In our simulations, the positions
considered by most theories[6,25,33-35]. Thus, the actual value of νeff is generally of limited interest, it only gives an indication to whichpart of an extended crossover region the data belong. However,we emphasize that: (i) our range of N nicely corresponds tothe range available in experiments[1,2,21-23,32,46-48] and (ii) the analysis in term of power laws with effective exponents isa standard practice of experimentalists in this context.A simulation analysis for the static properties of bottle-brushmacromolecules with flexible backbone have been discussed in detail previously[15].In this work we rather focus on the overall shapes that suchmacromolecules obtain, and discuss various aspects that couldnot be discussed in the frame of effective exponent analysis.In our simulations, the positions 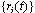 of the effective monomers with label i evolve in time t according toNewton's equation of motion, amended by the Langevinthermostat[37-49]
of the effective monomers with label i evolve in time t according toNewton's equation of motion, amended by the Langevinthermostat[37-49]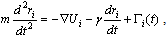 | (3) |
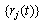 ,γ is the friction coefficient, and Γi(t) is the associated random force. The latter is related to γ by the fluctuation-dissipationrelation
,γ is the friction coefficient, and Γi(t) is the associated random force. The latter is related to γ by the fluctuation-dissipationrelation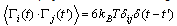 | (4) |
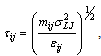 | (5) |
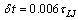 , and utilizing the GROMACS package[51]. For the calculation of properties of the bottle brushes, typically 500 statistically independent configurations are averaged over. Of course, for bottle-brushes with large Nb equilibration of the polymer conformations is a difficult problem. Since we expect that end-to-end distance Re and gyration radius Rg of the whole molecule belong to the slowest relaxing quantities, the judgment of the quality of results was based on the autocorrelations function of either of these quantities[15].
, and utilizing the GROMACS package[51]. For the calculation of properties of the bottle brushes, typically 500 statistically independent configurations are averaged over. Of course, for bottle-brushes with large Nb equilibration of the polymer conformations is a difficult problem. Since we expect that end-to-end distance Re and gyration radius Rg of the whole molecule belong to the slowest relaxing quantities, the judgment of the quality of results was based on the autocorrelations function of either of these quantities[15].3. Results and Discussion
- The interplay of various length scales in bottle-brush macromolecules results in interesting structures. The most extreme cases for the present system are shown in Fig. 1. For small values of N and temperatures close to theta (T = 3.0), the molecule can adopt conformations like the one of Fig. 1a, or that of Fig. 1b where still locally the backbone holds a high local flexibility. Moreover, at higher temperatures (e.g., T = 4.0, Figs. 1c and d) the whole macromolecule stretches due to the high affinity with the solvent molecules (Figs. 1c and d). Due to the longer side chains (N = 40, Fig. 1c) the backbone end beads are now not able to come close to each other due to the presence of the side chains which stretch the backbone monomers in the directions parallel to the backbone ends. It is clear that the side chains cause a significant stiffening of the backbone, at least on a coarse-grained scale, and that bottle brushes where Nb is not very much larger than N look like wormlike chains. It has been shown that, for temperatures close to the theta temperature, bottle-brush molecules can be very well described by the Kratky-Porodmodel[15], which describes the crossover from rods to Gaussian chains. Such analysis was based on the discussion of bond orientationcorrelations along the backbone beads, the measurement of the end-to-end distance and the use of effective exponents[15].Here, we show plots (Figs. 2 -5) of an alternative definition of a “local” persistence length lp(k) with the bond vector αk connecting monomers at positions rk and rk-1 (αk = rk– rk-1)[16,30,52]
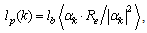 | (6) |
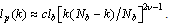 | (7) |
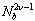 as
as 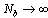 [4,52]. Furthermore, this problem is not improved when one considers an average of lp(k) along the chain[5,16], while no divergence occurs for lp(1)[16]. However, the use of lp(1) is inconvenient in simulations due to the limited statistical accuracy. However, it is interesting to see that this definition in agreement with previous work[15] gives distinct dependence of the “persistence length” both on Nb and thesolvent quality.
[4,52]. Furthermore, this problem is not improved when one considers an average of lp(k) along the chain[5,16], while no divergence occurs for lp(1)[16]. However, the use of lp(1) is inconvenient in simulations due to the limited statistical accuracy. However, it is interesting to see that this definition in agreement with previous work[15] gives distinct dependence of the “persistence length” both on Nb and thesolvent quality.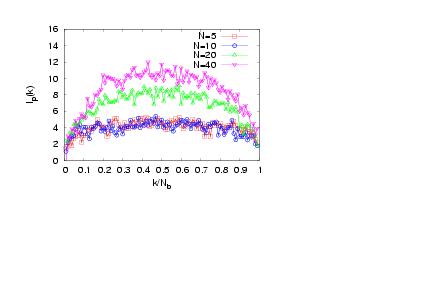 | Figure 2. (Colour online) Local persistence length lp(k) plotted versus k / Nb for σ = 0.5, Nb = 100, and T = 3.2 for different chain lengths N, as indicated |
 | Figure 3. (Colour online) Local persistence length lp(k) plotted versus k / Nb for σ = 0.5, Nb = 100, and T = 4.0 for different chain lengths N, as indicated |
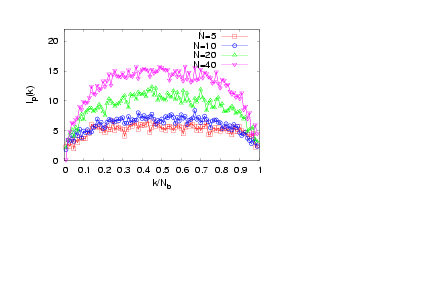
 | Figure 4. (Colour online) Local persistence length lp(k) plotted versus k / Nb for σ = 1, Nb = 50, and T = 3.2 for different chain lengths N, as indicated |
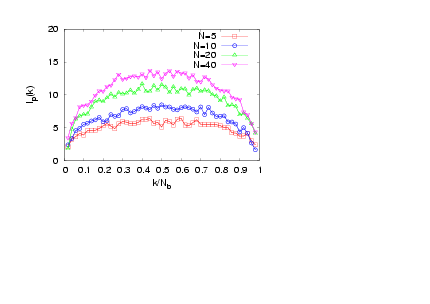
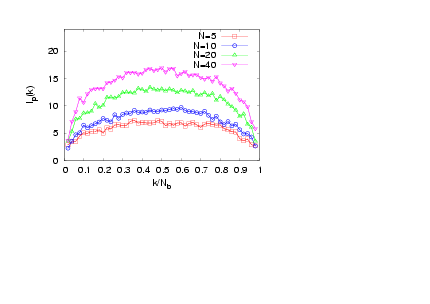 | Figure 5. (Colour online) Local persistence length lp(k) plotted versus k / Nb for σ = 1, Nb = 50, and T = 4.0 for different chain lengths N, as indicated |
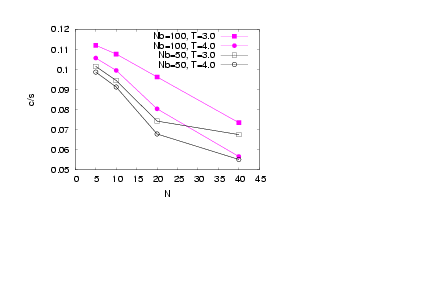
 | Figure 6. (Colour online) Average dihedral angle along the backbone measured in Radians plotted versus N for σ = 0.5 (open symbols) and σ=1.0(full symbols) for differentNb and T, as indicated |
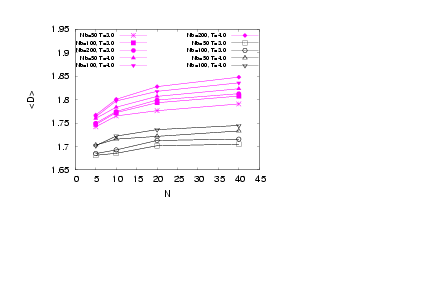
 there is a pronounced increase in D, which is mediatedfor N=40. Data also show a systematic increase in D as Nb increases showing that the local stiffness also clearly on average depends on Nb.
there is a pronounced increase in D, which is mediatedfor N=40. Data also show a systematic increase in D as Nb increases showing that the local stiffness also clearly on average depends on Nb.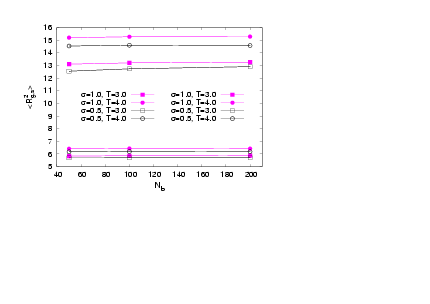 | Figure 7. (Colour online) The mean square gyration radius of the side chains versus Nb for different σand T. Full symbols refer to data with N=40, while open symbols to data with N=20 |
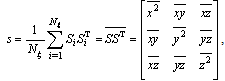 | (8) |
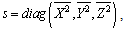 | (9) |
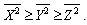 | (10) |
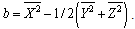 | (11) |
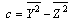 | (12) |
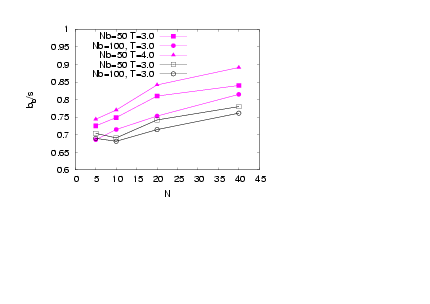 | Figure 8. (Colour online) Asphericity of the backbone beads versus N forσ=1.0 (full symbols) and σ=0.5 (open symbols) andvarious cases ofNb and T as indicated |
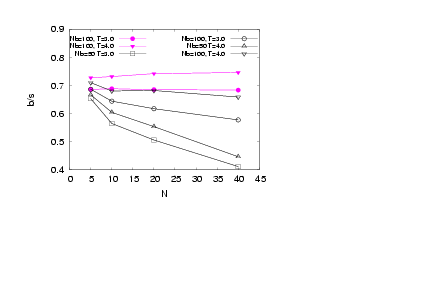 | Figure 9. (Colour online) A corresponding plot for the asphericity of the whole bottle-brush molecules is shown |
 effects dueto the backbone ends are smeared out. Also, the results for N = 20 exhibit higher values of normalized asphericity than those for the case N = 40, where the chain is more stretched inthe radial directions from the backbone.
effects dueto the backbone ends are smeared out. Also, the results for N = 20 exhibit higher values of normalized asphericity than those for the case N = 40, where the chain is more stretched inthe radial directions from the backbone.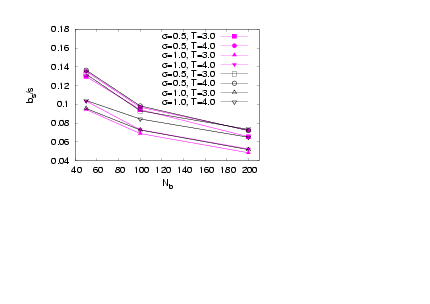 | Figure 10. (Colour online) Asphericity of the side chains versus Nbis plotted for two different side chain lenghts N = 20 (full symbols) and N = 40 (open symbols) for different σand T as indicated |
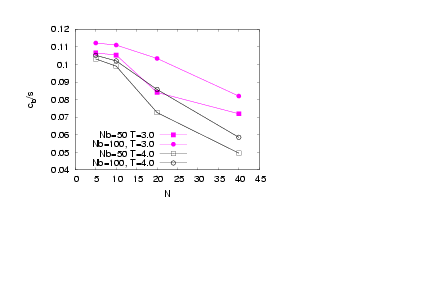 | Figure 11. (Colour online) Acylindricity of the backbone beads versus N for two different temperaturesT=3.0 (full symbols) and T=4.0 (open symbols)for σ = 1.0 and differentNbas indicated |
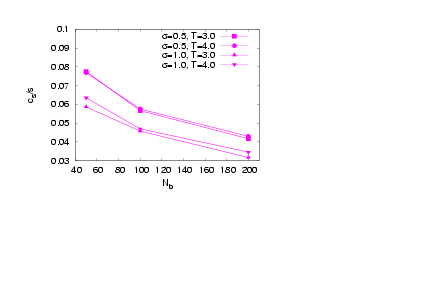 | Figure 13. (Colour online) Acylindricity of the side chains versus Nb for the case N = 20 and different grafting density σand temperature T, as indicated |
4. Conclusions
- In summary, we have demonstrated that the interplay of solvent quality, grafting density, side chain and backbone length in bottle brushes gives rise to very rich structural properties, where the distribution of monomers exhibit differences between bottle brushes, whereas other quantities would not reveal any dependence. A coarse-grained bead-spring model for bottle-brush polymers was studied via molecular dynamics, by varying both the chain length Nb of the backbone and the side chains N, for two values of the grafting density, under variable solvent conditions. The main target of the present work was to emphasize this geometric description of the shape of bottle-brush macromolecules at temperatures close to theta solvent conditions and in the good solvent regime. A short discussion on a way to extract the persistence length in bottle brushes and its relevant drawbacks was also briefly discussed for the present model.
ACKNOWLEDGEMENTS
- P.E.T. would like to thank Profs. K. Binder and W. Paul for an exceptional collaboration over the last years. This work has benefitted by their insight and discussions. He also acknowledges financial support by the Austrian Science Foundation within the SFB ViCoM (Grant No. F41).N.G.F. has been partly supported by MICINN, Spain, through Research Contract No. FIS2009-12648-C03.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML