A. Hassen 1, A. I. Ali 2, Bog G. Kim 3, A. Krimmel 4
1Department of Physics, Faculty of Science, Fayoum University, 63514 El Fayoum, Egypt
2Basic Science Department, Helwan University, Cairo, Kopry-El Qouba, Egypt
3Department of Physics, Pusan National University, Pusan, 609-735, Korea
4Technical Trainers College TTC, 11451 Riyadh, Kingdom of Saudi Arabia
Correspondence to: A. Hassen , Department of Physics, Faculty of Science, Fayoum University, 63514 El Fayoum, Egypt.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The structural, magnetic and electric properties of Pr1−xSr1+xCoO4 layered perovskite have been investigated systematically over the range of doping, 0 ≤ x ≤ 0.40. The Rietveld refinements of X- ray powder diffraction (XRD) patterns at room temperature indicate that the samples crystallize in the K2NiF4-type structure with group symmetry I4/mmm. The samples of 0 ≤ x < 0.20 show Curie-Weiss paramagnetic behavior. With increasing x (0.20 ≤ x ≤ 0.40), three magnetic transition temperatures can be identified. The ground state exhibits a spin glass (SG) phase below the spin glass transition temperature TSG . Above, there is a mixture of ferromagnetic (FM) and antiferromagnetic (AFM) short-range order for TSG< T < TM with TM denoting the temperature of the corresponding anomaly in the magnetic susceptibility data. The third state can be attributed to a Griffiths phase for TM < T <TG with TG being the transition temperature between the Griffiths phase and the paramagnetic high temperature state. While the SG phase was suppressed with increasing applied field, both TM and TG shifted towards lower temperatures. No indications for a single pure ferromagnetic phase were observed even for applied magnetic fields up to 60 kOe. The electrical resistivity of the samples shows either thermally activated semiconducting behavior or 2D variable range hopping. The results are summarized in (x−T) phase diagram and discussed with respect to structure-property relationships.
Keywords:
Pr1−xSr1+xCoO4, Crystal Structure, Magnetic Susceptibility, Magnetization, Spin Glass, Electrical Resistivity, Structure-Property Relationship
Cite this paper: A. Hassen , A. I. Ali , Bog G. Kim , A. Krimmel , Structure-Property Relationships in Pr1-xSr1+xCoO4, (0 ≤ x ≤ 0.40), American Journal of Condensed Matter Physics, Vol. 2 No. 4, 2012, pp. 93-100. doi: 10.5923/j.ajcmp.20120204.04.
1. Introduction
Perovskite cobalt oxides have attracted great interest because of both, their fundamental physical characteristics related to unique spin state transitions, as well as their technological importance[1–3]. The spin state transitions observed in perovskite cobaltates are different compared to those of perovskite manganites. The crystal-field splitting energy of d-state electrons (Ecf ) and Hund energy (Eex ) are comparable for perovskite cobaltates. This implies that the energy gap between the t2g and eg states is small and the electrons in t2g can be thermally excited into the eg state. As a result, complex magnetic properties not only arise in the original perovskite compounds R1−xSrxCoO3 which exhibit a rather isotropic three-dimensional (3-D) arrangement of magnetic ions; but also in layered perovskite systems R2−xSrxCoO4, R = La, Nd or Pr[2].The layered-type cobaltates A2BO4 with K2NiO4 structure are characterized by two- dimensional confinement of the B − O −B network that significantly reduces the eg electron bandwidth. In turn, electrons correlations are strong and can alter the interplay between the different microscopic degrees of freedom (lattice, charge, orbital and spin degrees of freedom). For instance, the magnetic state of La2-xSrxCoO4 transforms from antiferromagnetic (AFM) to ferromagnetic (FM) upon doping for x ≥ 0.6[4]. On the other hand, the zero field susceptibility of Nd1−xSr1−xCoO4 (for 0.25 ≤ x ≤ 0.6) shows different magnetic transitions[5]. The first is a spin-glass (SG) transition at 18 K as reported for layered manganites[6]. The magnetic frustration necessary for the formation of a spin glass state is attributed to the competition between double exchange (Co4+ - Co3+) and superexchange (Co3+ -Co3+ or Co4+-Co4+) interactions. The second transition is due to a Griffiths singularity around 210 K, i.e. the formation of short-range ferromagnetic clusters with large spins in the paramagnetic matrix.The electrical behavior of Nd1−xSr1+xCoO4 follows an Arrhenius law for x = 0.25, 0.33 and 0.60. This indicates that the temperature dependent resistivity of Sr-doped samples is semiconducting-like due to hopping of small lattice polarons, as in the case of manganites. Doping “dependent” charge and superstructures in Pr2−xCaxCoO4 (0.39 ≤ x ≤ 0.7) and La2−xSrxCoO4 (x = 0.40, 0.61) were reported[7]. It was found that the hole charge carriers in these doped cobaltates are strongly localized and therefore, thermal activated behavior was observed with an activation energy of the order of 0.5 eV. A systematic increase of the resistivity with decreasing A-site rare earth ionic radius r3+ in cobaltates was reported[8] implying that upon narrowing the bandwidth, the mobility of eg electrons is decreased. The activation energy of PrSrCoO4 is about 0.20 eV [8].Despite intense research activities in this field, there is no detailed analysis of the structural, magnetic and electric behavior of the substitutional series Pr1−xSr1+xCoO4. Here we report on a systematic study of the physical properties of these layered perovskites as a function of doping to understand the complex interplay between spin, charge and lattice/orbital degrees of freedom. The results are summarized in (x−T) phase diagram and discussed based on structure-property relationships.
2. Experimental
Polycrystalline Pr1−xSr1+xCoO4 samples (0 ≤ x ≤ 0.4) were prepared by the solid state method. Stoichiometric mixtures of Pr6O11 (4N, MTI), SrCO3 (5N, Cerac) and Co3O4 (4N, Aldrich) were well ground and palletized. Then the specimen were calcined at 1000℃ and sintered in oxygen at 1050 ∼1150℃ for 48 h with intermediate grindings. The sintered samples were annealed in oxygen at 1200℃ for 48 h. These pellets were further annealed at lower temperature (550-600℃) for 24 h in oxygen overpressure in order to achieve the high oxidation state. The samples were confirmed to be single phase by x-ray diffraction (XRD) using Cu Kα radiation (Bruker D8). The XRD data were analyzed by standard Rietveld refinement employing the FULLPROF program suite[9].DC magnetization measurements were performed in a SQUID magnetometer (Quantum Design MPMS-5S). Temperature dependent magnetization (M-T) curves were measured in zero-field-cooled (ZFC) mode between 5 and 300K with an applied magnetic field (H) of 100 Oe and 5000 Oe, respectively. The field dependent magnetization (M-H) was measured within H = ± 60 kOe at 5K. The temperature dependence of the electrical resistivity, ρ(T), was measured both on cooling and on heating (from 10 to 300 K) by the standard dc four-probe method using a CCR type refrigerator.
3. Results and Discussion
3.1. X-Ray Diffraction
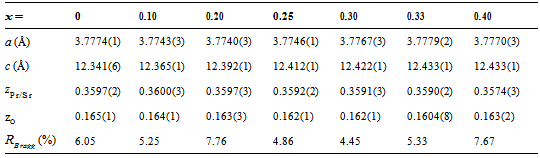
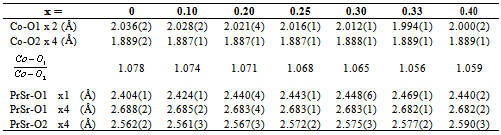
Polycrystallines Pr1−xSr1+xCoO4 (x = 0, 0.10, 0.20, 0.25, 0.30, 0.33, 0.40) were characterized by conventional powder x-ray diffraction at room temperature employing Cu-Kα radiation. All investigated samples crystallize in the K2NiF4-type structure[10]. The crystal structure is described by space group I4/mmm (No. 139) with Pr/Sr ions at the Wyckhoff position 4e (0, 0, z) (z ≈ 0.35), Co ions at the 2a site (0, 0, 0) and oxygen ions at the 4c site (1/2, 0, 0) and the 4e site (0, 0, z) (z ≈ 0.16), respectively. The diffraction patterns showed single phase material for all investigated compounds. In particular, no indications of spurious perovskite-related phases could be detected. Fig. 1 shows representative diffractograms and the corresponding refinements of Pr1−xSr1+xCoO4 for x = 0, 0.25, 0.33. The Rietveld refinements included the following fit parameters: overall scale factor, zero point shift, peak shape, isotropic temperature factors, 3 Cagliotti resolution parameters, the lattice constants a and c, the atomic positional parameters zPr/Sr and zO of Pr/Sr and oxygen ions, respectively. Pronounced preferred orientation effects were observed in particular for x = 0.20 and x = 0.30 and were corrected using the March function of the FULLPROF program. Good agreement between observed and calculated intensities is achieved as reflected in the reliability factors. The structural properties of Pr1−x Sr1+xCoO4 are summarized in Table 1. The results show good agreement with values published in the literature[10].Table 1. Structural parameters of Pr1-xSr1+xCoO4 for 0 ≤ x ≤ 0.40 as resulting from the Rietveld refinements of the X-ray powder diffraction measurements. Space group is I4/mmm with Pr/Sr ions at the 4(e) site with fractional coordinates (0, 0, z), Co ions at 2(a) sites with coordinates (0, 0, 0), oxygen O1 at the 4(c) site (0.5, 0, 0) and oxygen O2 at the 4(e) site (0, 0, z). Calculated standard deviations are given in parentheses
 |
| |
|
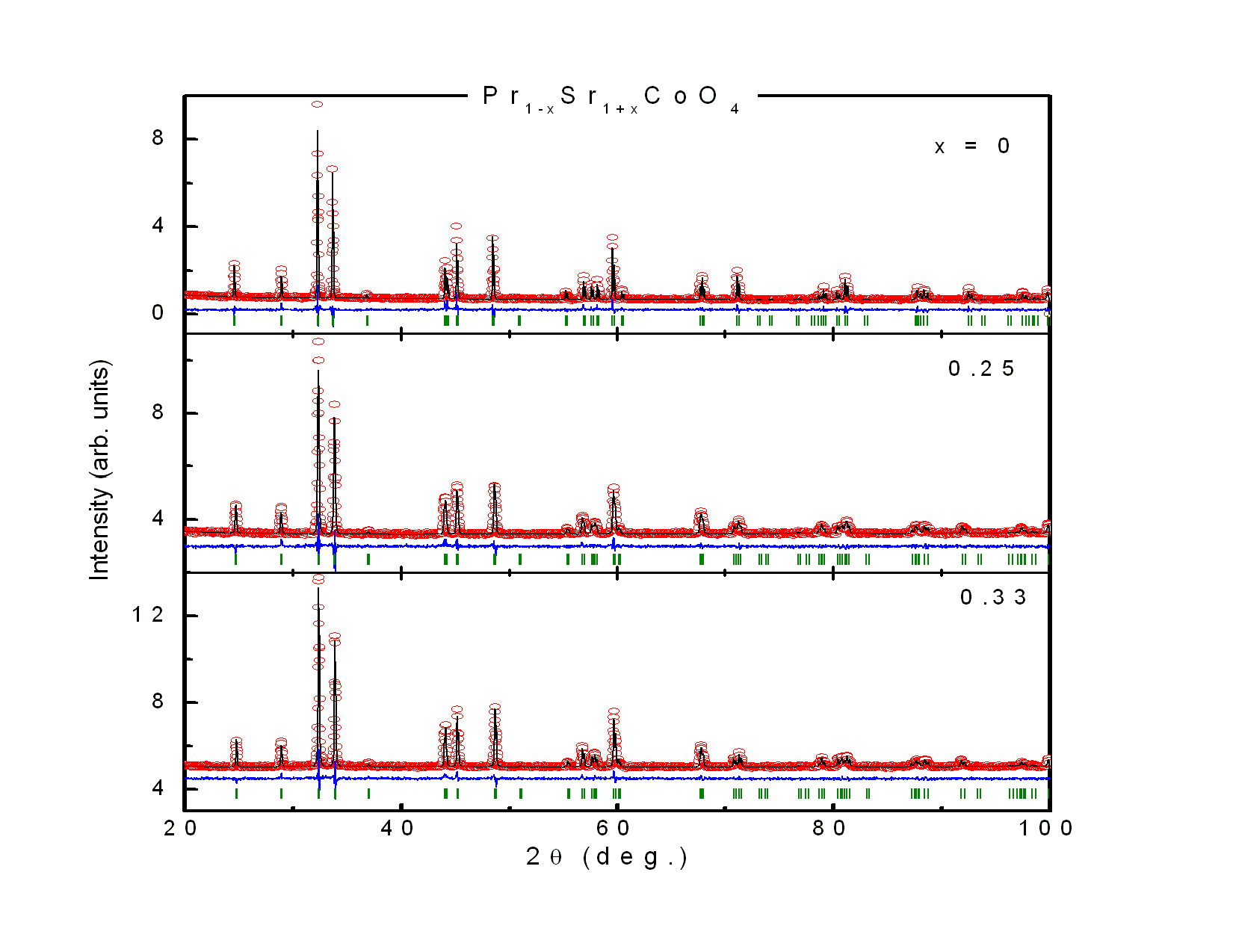 | Figure 1. X-ray diffraction patterns of some samples of Pr1-xSr1+xCoO4 system. Shown are observed intensities (open red circles), calculated intensities (full black line), their difference (blue line below), and the position of the calculated reflections (green vertical bars) |
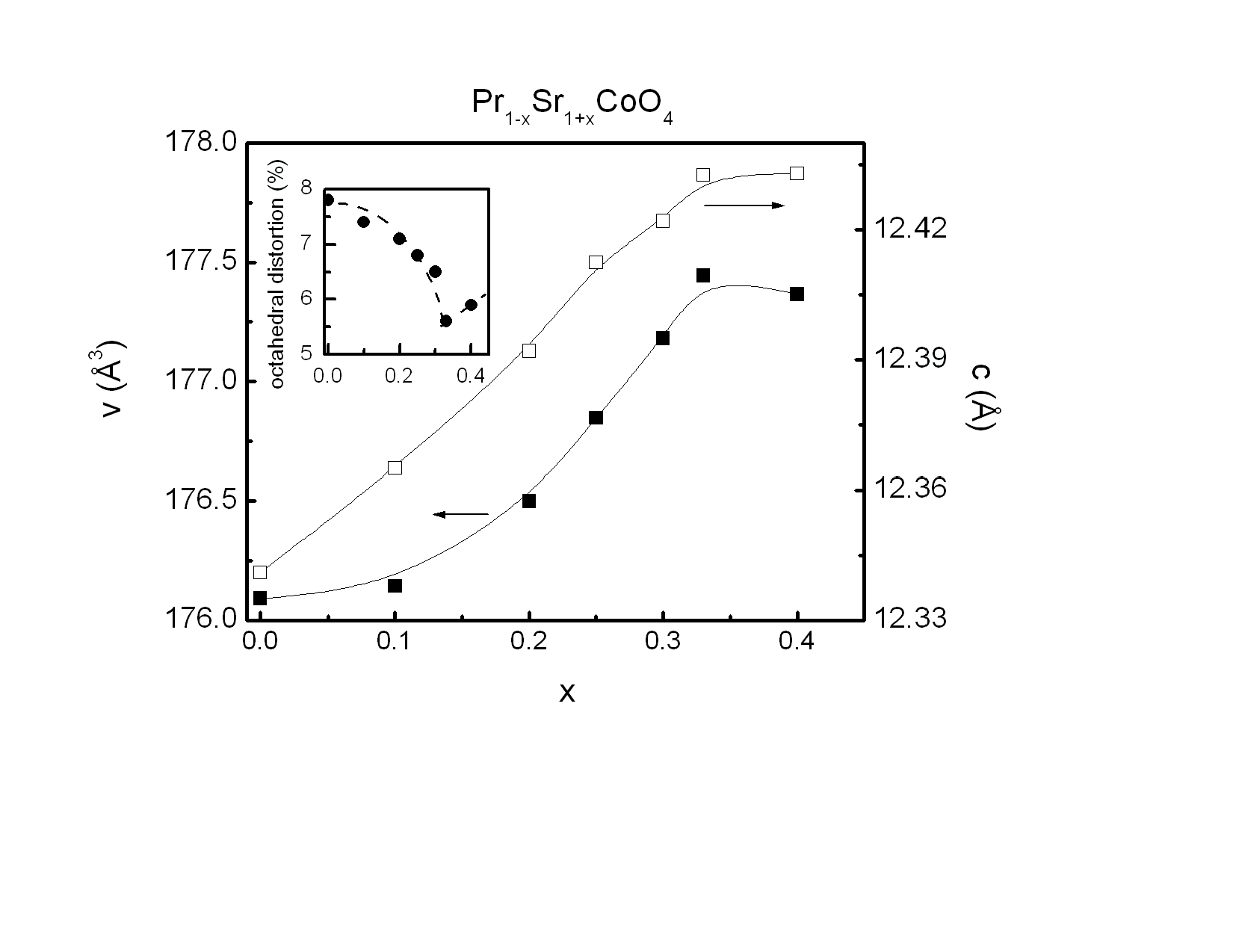 | Figure 2. Lattice constant c (open squares, right scale) and unit cell volume V (closed squares, left scale) of Pr1-xSr1+xCoO4 as determined from the Rietveld refinements of the x-ray diffraction measurements. The inset shows the octahedral distortion as the ratio of the two different Co-O bond lengths. Lines are guides to the eye |
The unit cell volume increases with increasing Sr concentration, as illustrated in Fig. 2 Interestingly, this change of the unit cell volume is predominantly originating by an increase of the tetragonal lattice constant c (see Fig. 2), whereas the lattice constant a within the equatorial plane remains almost constant. This behavior is similar to a previous study[10] on Pr1−xSr1+xCoO4 and the results found for the La, Nd and Gd homologue compounds[11]. It emphasizes the quasi two-dimensional character of the K2NiF4-type structure representing the n = 1 end member of the Ruddlesden-Popper phases. The concentration dependence of the unit cell volume is governed by two competing effects. The substitution of Pr3+ (ionic radius for ninefold coordination is r(Pr3+) = 1.179 Å) by Sr2+ (r (Sr2+) = 1.31 Å) leads to a lattice expansion. On the other hand, charge neutrality then implies oxidation of Co3+ (ionic radius for high spin state in sixfold coordination is r(Co3+) = 0.545 Å) to Co4+ (r(Co4+) = 0.53 Å). The substitution of Pr by Sr is the dominating effect, in particular at low doping levels.The refinements allow a determination of the bond length listed in Table 2. The ratio of the Co-oxygen bonds (apical bond length over equatorial bond length) reveals the distortion of the CoO6 octahedra. This octahedral distortion clearly decreases upon increasing Sr concentration up to x = 0.33. This behavior is directly reflected in the z-coordinateof oxygen. The octahedral distortion is shown in the inset of Fig. 2. However, on further increasing Sr content from x = 0.33 to x = 0.40, both the z-coordinate of oxygen, as well as the distortion reveal a significant increase. A common method to analyze the octahedral buckling in perovskite related transition metal oxides is the tolerance factor t defined as 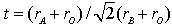 . In the present case, rA represents the average ionic radius of Pr3+ and Sr2+, rB is the mean ionic radius of Co3+ and Co4+ and rO is the ionic radius of O2-. t = 1 corresponds to the ideal cubic perovskite structure. Decreasing values of t < 1 indicate an increasing buckling of the octahedra with a lowering from cubic to tetragonal/orthorhombic symmetry for t < 0.97. For fixed ionic radii, the substitutional series like Pr1−xSr1+xCoO4 necessarily exhibit a linear dependence of the tolerance factor t on concentration, as shown in Fig. 3 for intermediate spin (IS) and high spin (HS) configurations of Co3+, respectively. Similar behavior was observed for La2−xSrx CoO4 system[12]. The ionic radius of Co ions changes depending on their spin state. Taking r(Co3+) = 0.577 Å for the intermediate (IS) spin state and r(Co3+) = 0.61 Å for the high (HS) spin state results in a change from t = 0.962 to 0.952 which fits well with the bond length listed in Table 2. The structural data thus point towards a spin state transition from an IS to a HS sate of Co3+ ions in Pr1-xSr1+xCoO4 on going from x = 0.33 to x = 0.40. The crystal structure is now sufficiently large to accommodate high spin Co ions.
. In the present case, rA represents the average ionic radius of Pr3+ and Sr2+, rB is the mean ionic radius of Co3+ and Co4+ and rO is the ionic radius of O2-. t = 1 corresponds to the ideal cubic perovskite structure. Decreasing values of t < 1 indicate an increasing buckling of the octahedra with a lowering from cubic to tetragonal/orthorhombic symmetry for t < 0.97. For fixed ionic radii, the substitutional series like Pr1−xSr1+xCoO4 necessarily exhibit a linear dependence of the tolerance factor t on concentration, as shown in Fig. 3 for intermediate spin (IS) and high spin (HS) configurations of Co3+, respectively. Similar behavior was observed for La2−xSrx CoO4 system[12]. The ionic radius of Co ions changes depending on their spin state. Taking r(Co3+) = 0.577 Å for the intermediate (IS) spin state and r(Co3+) = 0.61 Å for the high (HS) spin state results in a change from t = 0.962 to 0.952 which fits well with the bond length listed in Table 2. The structural data thus point towards a spin state transition from an IS to a HS sate of Co3+ ions in Pr1-xSr1+xCoO4 on going from x = 0.33 to x = 0.40. The crystal structure is now sufficiently large to accommodate high spin Co ions.Table 2. Bond lengths of Pr1−xSr1+xCoO4 for 0 ≤ x ≤ 0.40 as resulting from the Rietveld refinements of the x-ray powder diffraction measurements
 |
| |
|
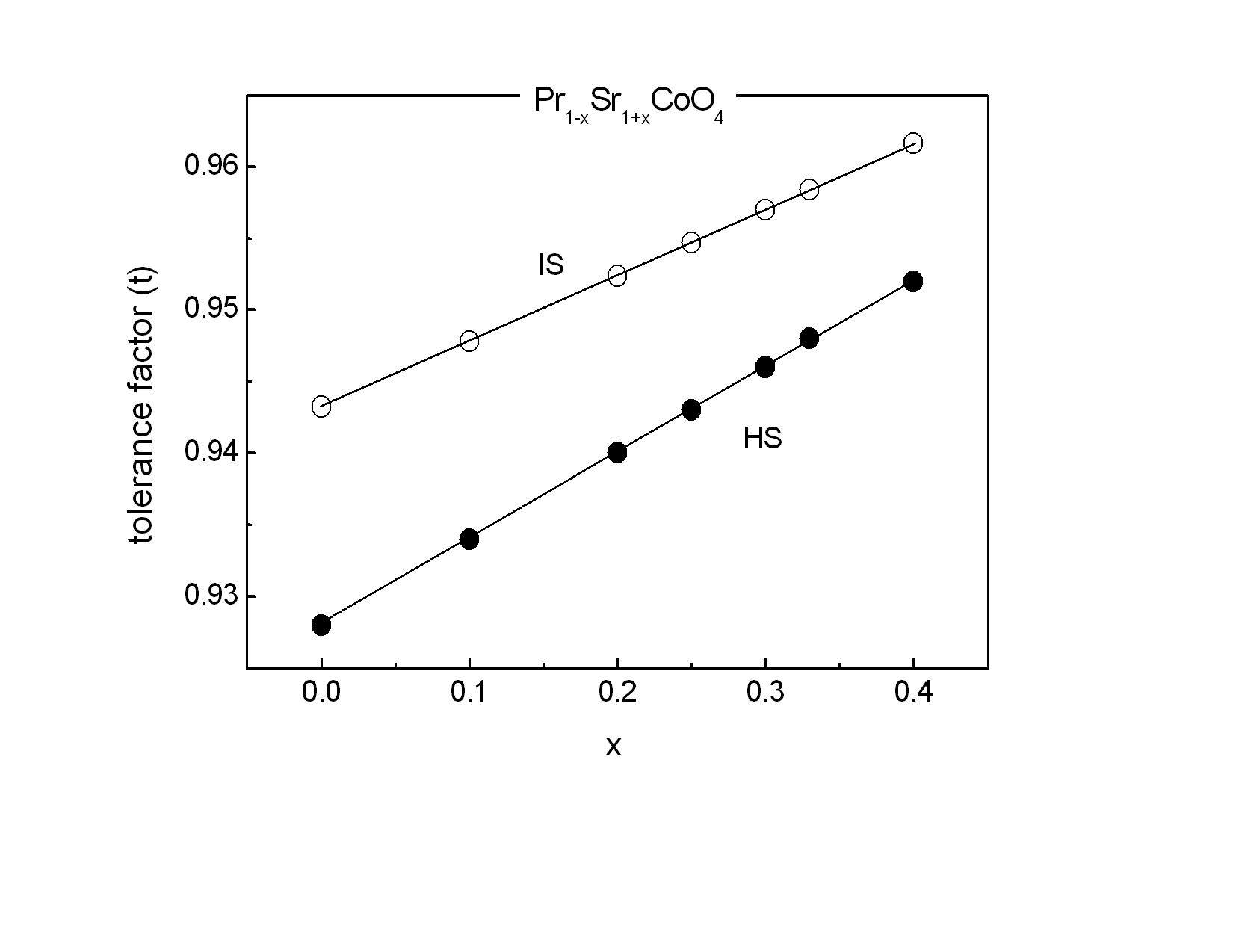 | Figure 3. Tolerance factor t of Pr1-xSr1+xCoO4 for the intermediate spin (IS) and high spin (HS) configuration of Co3+ ions |
3.2. Magnetic Properties
The temperature dependence of the zero field-cooled (ZFC) magnetic susceptibility, χ, collected at 100 Oe of Pr1−xSr1+xCoO4, 0 ≤ x ≤ 0.40 is shown in the upper frame of Fig. 4. The samples of x = 0 and x = 0.10 exhibit Curie-Weiss paramagnetic behavior in the whole temperature range as shown in the inset of Fig. 4. A pronounced increase of χ(T) upon cooling was observed for x = 0.20 with a cusp at ∼16 K due to a spin glass (SG) transition (TSG). No traces of a Griffiths phase were identified for this level of doping as reported earlier[13]. All compounds with 0.20 ≤ x ≤ 0.40 reveal spin glass anomalies with the highest spin glass transition temperatures of TSG ∼ 22 K observed for the compounds of x = 0.30 and 0.33. Similar SG transitions were observed at 25 K for La1−xSr1+xMnO4 (x = 0.2, 0.40)[6] and at 10 K for LaSrCoO4 [14].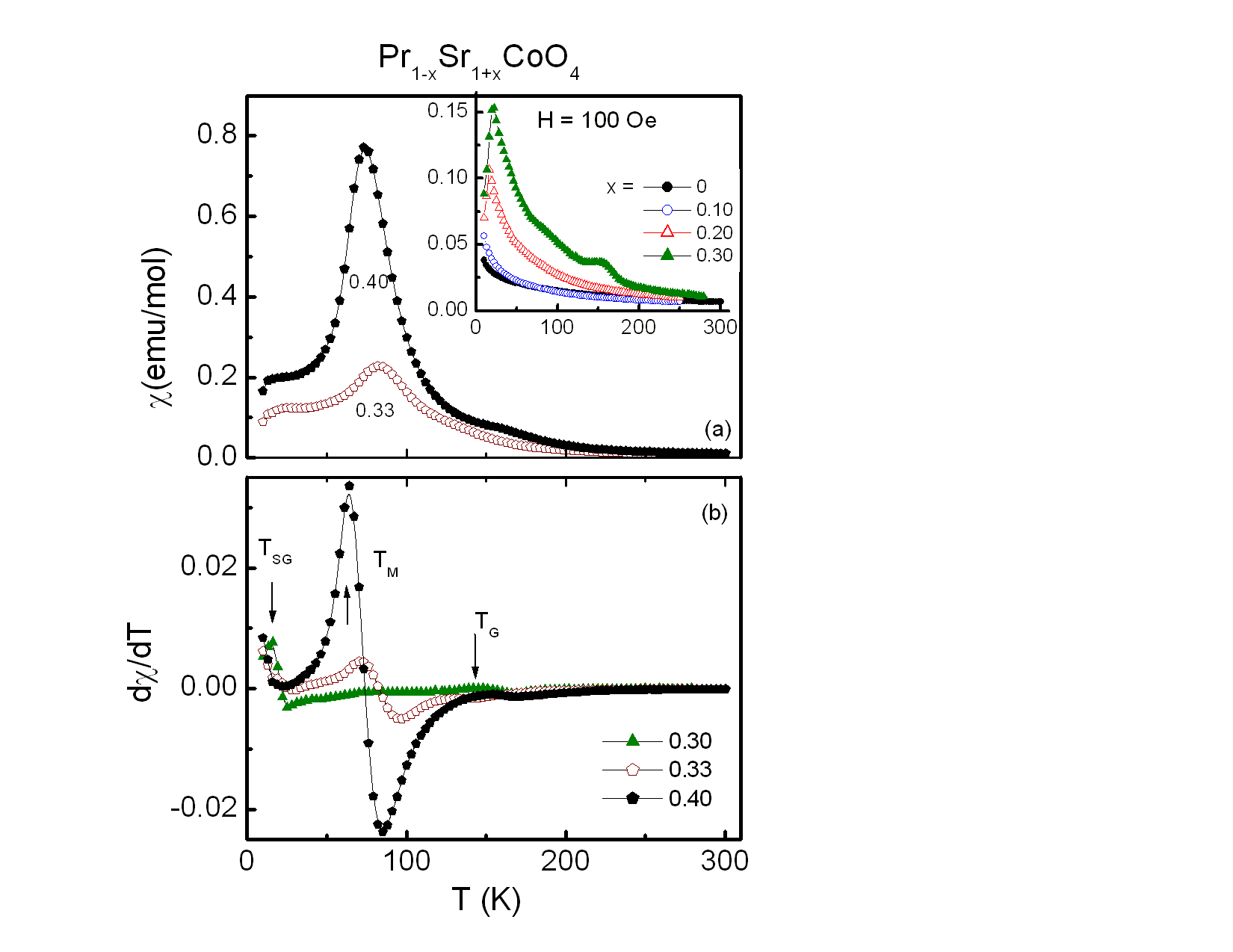 | Figure 4. The upper frame (a) with the inset represent the zero-field cooled susceptibility χ(T) of the investigated Pr1-xSr1+xCoO4, 0 ≤ x ≤ 0.4, samples at H = 100 Oe. The lower frame (b) shows dχ/dT versus T. The corresponding magnetic transitions are indicated by arrows |
The transition temperatures of the different magnetic phases are more clearly identified by plotting dχ/dT versus T as shown in the lower frame of Fig. 4. Comparison with previous results leads us to identify two transitions indicated by arrows in the lower frame of Fig. 4. TG ≈ 145 K and TM ≈ 73 K for the sample of x = 0.30. The values of TG shift to 127 K for x = 0.33 and 154 K for x = 0.40. TG refers to a Griffiths singularity, i.e., the formation of short-range ferromagnetic clusters with large spins in the paramagnetic matrix. Such Griffiths singularities were also observed at 200 K for La0.5Sr1.5CoO4 as in[14] and at 100 K for Rb2Co1−xMnxF4[15]. A similar behavior was reported for Nd1−xSr1+xCoO4, x = 0.25, 0.33 and 0.60[5]. Below the Griffiths phase and before entering the spin glass phase there is an intermediate short range ferromagnetic phase for TSG < T < TM. As derived from dχ/dT, T is about 70 K and 64 K for the samples of x = 0.33 and 0.40, respectively. Whereas the substitution of Pr by Sr ions strengthen the ferromagnetic exchange, no long range ordered FM phase was found, as discussed below.To further study these complicated magnetic transitions of Pr1−xSr1+xCoO4, the ZFC magnetic susceptibility of all investigated compounds was measured at 5000 Oe, as depicted in Fig. 5. Again, χ(T) increases with increasing Sr concentration x as evident from Fig. 5. The spin-glass transition, TSG, was suppressed with increasing field and the magnetic transitions became broad and shifted towards lower temperatures. As seen clearly in a corresponding plot of dχ/dT versus temperature in the lower frame of Fig. 5, TG and TM for x = 0.30, are 143 K and 76 K, respectively. On the other hand, the samples of x ≥ 0.30 undergo magnetic transitions at TM = 40 K and TG = 85 K.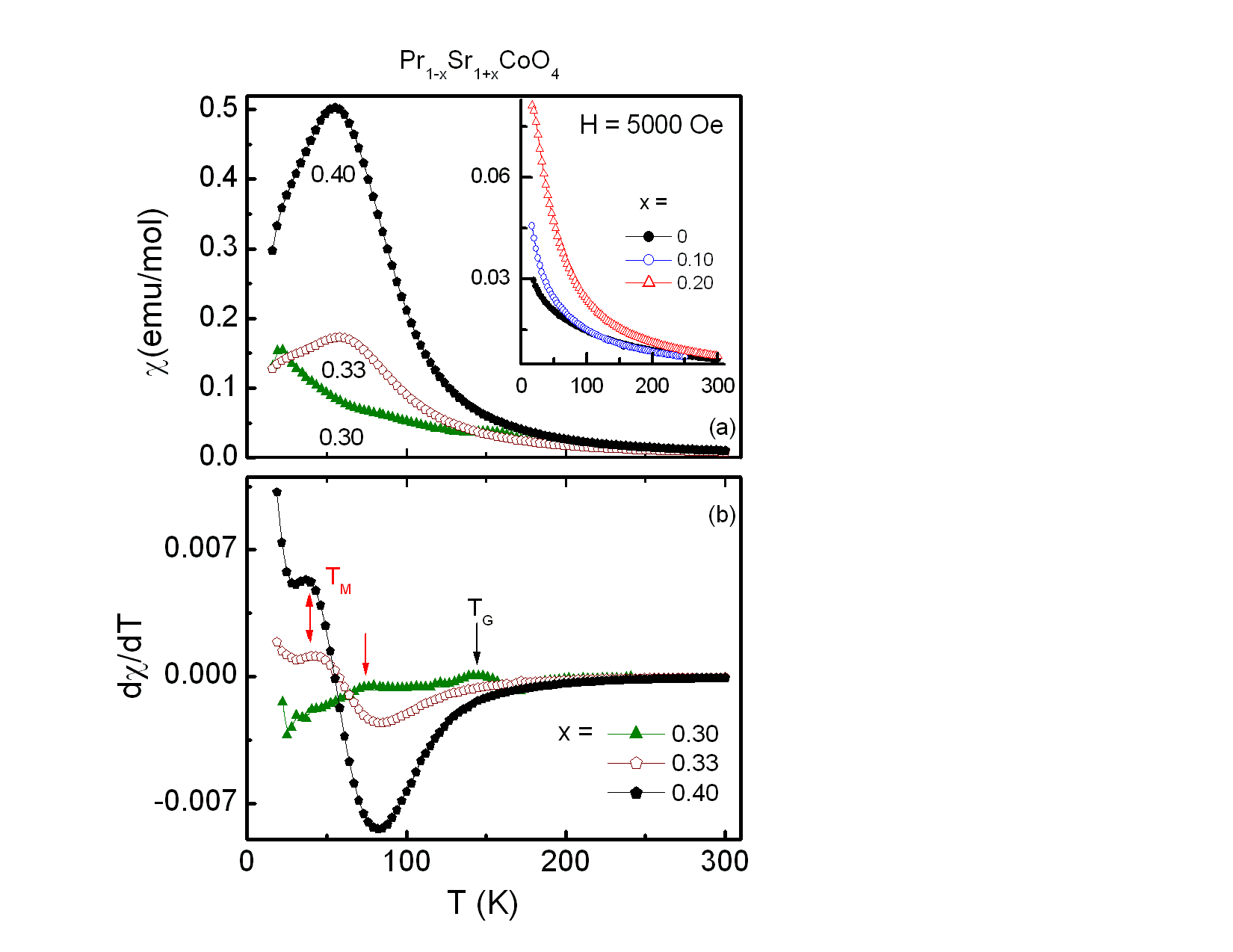 | Figure 5. (a) The upper frame and the inset represent the zero-field cooled susceptibility χ(T) of the compounds Pr1-xSr1+xCoO4, 0 ≤ x ≤ 0.4, in an applied magnetic field of H = 5000 Oe. (b) The lower frame shows dχ/dT versus T for x = 0.30, 0.33, 0.40 with the corresponding magnetic transitions indicated by arrows |
A Curie-Weiss behavior is observed over the entire temperature range for the samples of x = 0 and x = 0.10. Deviations from CW behavior at low temperatures were observed for higher doping levels x and the paramagnetic CW behavior is limited to high temperatures T > 150 K. Based on the CW law, the effective paramagnetic moments, µeff, and Curie-Weiss temperatures, Tθ , were calculated and listed in Table 3. The Curie-Weiss temperature Tθ alters from negative values for x ≤ 0.10 to positive values for x ≥ 0.20 and increases gradually with increasing x. Similar behavior was also observed for the La1−xSr1+xCoO4 with increasing x [16]. The change of sign of Tθ with x shows that the substitution of Pr3+ by Sr2+ ions changes the magnetic interactions from predominantly AFM to FM. The interplay between these different magnetic interactions provides the basis for the complex magnetic behavior. The determined values of the Curie constant (C) and Tθ enable us to estimate the CW susceptibility, 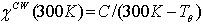 [17, 18] and the contribution of the permanent magnetic moments at room temperature. The differences of the magnetic parameters Tθ and µeff for different applied magnetic fields of 100 Oe and 5000 Oe are small and therefore, only values for H = 5000 Oe are listed in Table 3. As shown in Table 3, χCW(300 K) exhibits an overall increase with increasing Sr content due to increasing magnetic exchange. The effective paramagnetic moment µeff shows only moderate changes upon increasing Sr doping x. The magnetic dilution by substituting rare earth Pr3+ by Sr2+ is, at least to a major part, compensated by an increase of the magnetic moments in the Co sublattice. The presence of the rare earth ions leads to a shift of the effective paramagnetic moments µeff as compared to La1−xSr1+xCoO4 [14].
[17, 18] and the contribution of the permanent magnetic moments at room temperature. The differences of the magnetic parameters Tθ and µeff for different applied magnetic fields of 100 Oe and 5000 Oe are small and therefore, only values for H = 5000 Oe are listed in Table 3. As shown in Table 3, χCW(300 K) exhibits an overall increase with increasing Sr content due to increasing magnetic exchange. The effective paramagnetic moment µeff shows only moderate changes upon increasing Sr doping x. The magnetic dilution by substituting rare earth Pr3+ by Sr2+ is, at least to a major part, compensated by an increase of the magnetic moments in the Co sublattice. The presence of the rare earth ions leads to a shift of the effective paramagnetic moments µeff as compared to La1−xSr1+xCoO4 [14].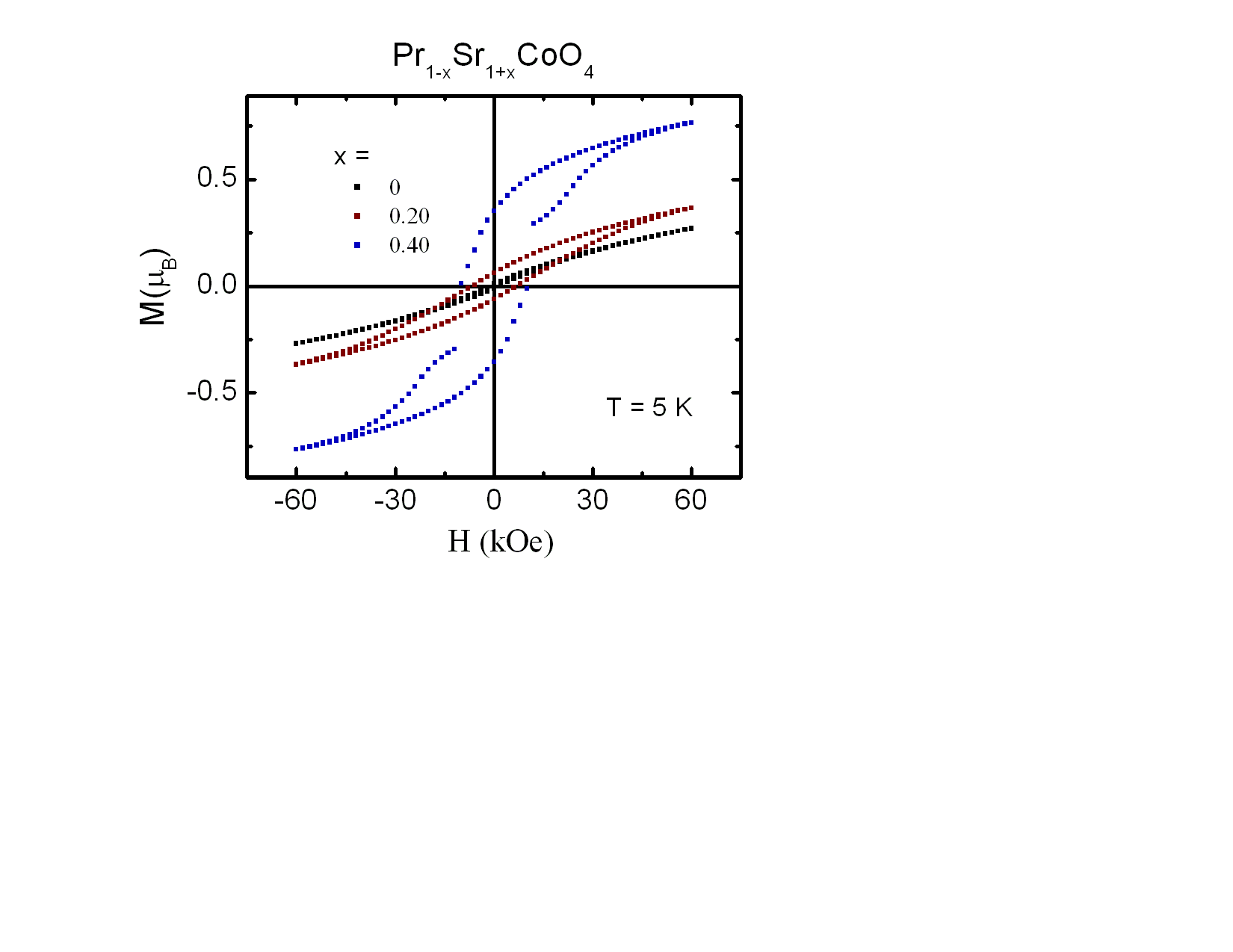 | Figure 6. Magnetization hysteresis of Pr1-xSr1+xCoO4 versus applied field (H) for selected concentrations x = 0, 0.20 and 0.40. The hysteresis curves of x = 0.25, 0.30 and 0.33 (not shown) reveal only slight differences |
To give more evidence about the absence of a fully developed FM phase, the magnetic hysteresis of some selected samples are displayed in Fig. 6 at T = 5 K. The paramagnetic behavior of PrSrCoO4 is evidenced by negligible hysteresis although M(H) shows slight deviations from a strict linear behavior. The area of the hysteresis loop increases as well as there is a tendency of M to saturate with increasing x. As a result, remnant magnetization (Mr), maximum magnetization at 5K, Mmax,5K, and coercive field (Hco ) increase with increasing the level of doping (see Table 3). However, none of the investigated samples shows full saturation.
3.3. Electrical Properties
The temperature dependence of the resistivity, ρ(T ), for Pr1−xSr1+xCoO4, 0 ≤ x ≤ 0.40 is depicted in Fig. 7. It is observed in the upper frame of figure 7 that ρ(T ) exhibits semiconducting characteristics (dρ/dT<0) for all compositions, consistent with results reported earlier[13]. The decrease of the room temperature resistivity, ρ300K , with increasing Sr content is given in Table 3. Such a decrease of ρ with increasing Sr concentration was also found for polycrystalline samples of La1−xSr1+xCoO4[14]. The relationship between ρ and T follows Arrhenius law for thermally activated semiconductors: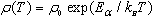 | (1) |
where ρ0, Ea and kB are a material constant, the activation energy and Boltzmann’s constant, respectively. To determine Ea, the variation of ln(ρ) as a function of 1/T is shown for x = 0, 0.10, 0.20, 0.40 in the lower frame of Fig. 7.The calculated values of Ea are listed in Table 3.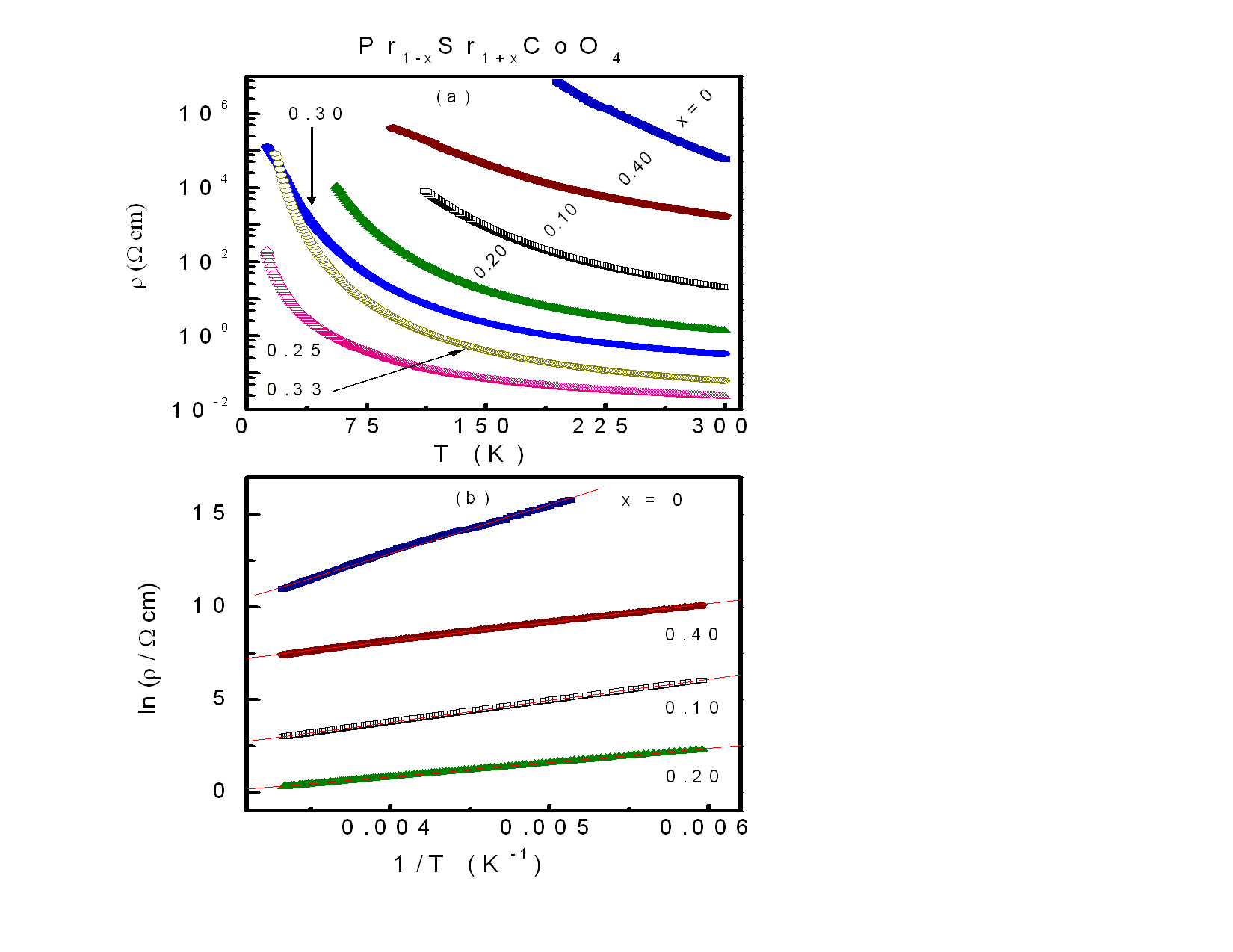 | Figure 7. (a) The resistivity as a function of temperature of x of Pr1-xSr1+xCoO4 system. (b) The variation of ln(ρ) against 1/T for some selected samples. The solid lines display the linear fitting. |
Table 3. Magnetic and electrical transport properties of Pr1−x Sr1+x CoO4 for 0 ≤ x ≤ 0.40. Listed are the Curie-Weiss temperature Tθ , the effective paramagnetic moment, μeff , the maximum magnetization at 5 K, Mmax,5K , the calculatesd CW magnetic susceptibility χCW(300 K), the coercive field H-co , the remnant magnetization Mr , the room temperature resistivity, ρ-300K , and the activation energy Ea for samples showing thermally activated behavior
 |
| |
|
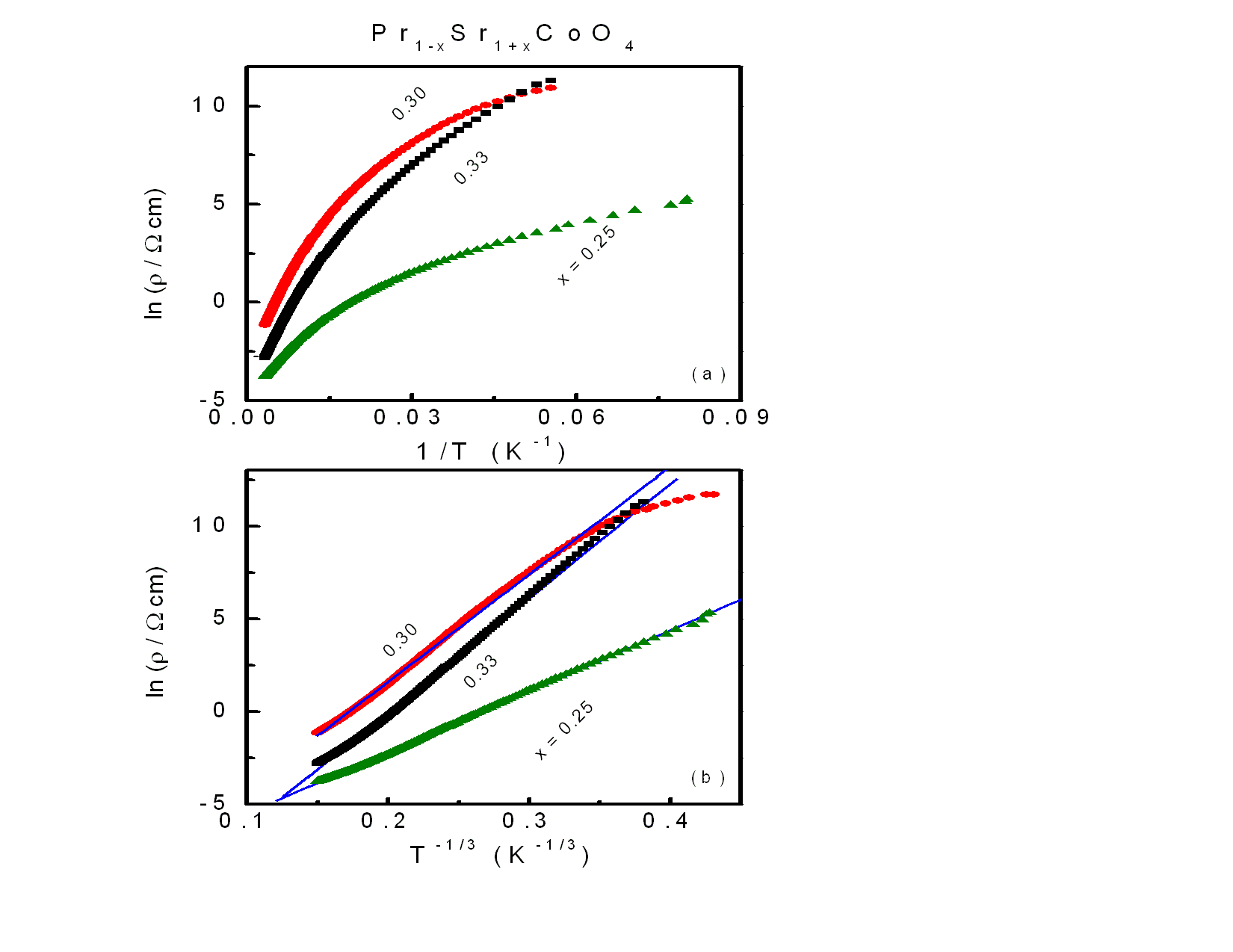 | Figure 8. (Upper frame) The variation of ln(ρ) against 1/T for the samples x = 0.25, 0.30 and 0.33. (Lower frame) ln(ρ) versus T-1/3 for the same samples. The solid lines display the fitting according to 2D-VRH model. |
The compositions with x = 0.25, 0.30 and 0.33 did not exhibit linear behavior with 1/T as shown in the upper frame of Fig. 8. The temperature dependent resistivity ρ(T) for the samples of x = 0.25, 0.30 and 0.33 can be fitted by Mott’s two-dimensional variable range hopping (2D-VRH) model [13, 19]: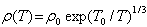 | (2) |
where ρ0 is constant and T0 is the variable-range hopping parameter described by Mott and Davis[20]. The magnitude of T0 can be used as a measure of the VRH phenomenon and it relates the density of states (g) near the Fermi level to the localization length (fo ) by [19],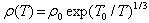 | (3) |
where kB is Boltzmann’s constant and β a numerical factor ∼21 [19, 21, 22]. According to Eq. (2), the fitting of ln(ρ) vs T-1/3 yields two parameters T0 and ρ0. As seen in the lower frame of Fig. 8, the 2D-VRH model is a good fit of ρ(T) for these three compounds. The values of T0 are 0.4, 2 and 2.3 106 K for x = 0.25, 0.30 and 0.33, respectively. The corresponding values of ρ0 for these samples are 0.02, 0.85 and 4.4 x 10−6 (Ω cm), respectively. To get the values of g, the exact value of fo should be determined from the proper knowledge of the dielectric constant (ε) by 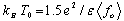 where e is the electronic charge[23].
where e is the electronic charge[23].
3.4. Phase Diagram and Structure Property Relationships
Based on structural, magnetic and electrical properties discussed above, the corresponding x−T phase diagram for Pr1-xSr1+xCoO4 was constructed as shown in Fig. 9. Magnetic transition temperatures have been taken from dχ/dT at 100 Oe applied field. The parent compound PrSrCoO4 is a paramagnetic insulator (PMI) within the studied range of temperatures. Therefore, this sample exhibits the lowest Tθ and Mmax,5K although it shows a higher µeff because of the large magnetic moment of Pr ions. With increasing Sr concentration, three magnetic transitions can be identified. Both Mmax,5K and Tθ increases gradually while µeff decreases slightly. For 0.20 ≤ x ≤ 0.40, a spin glass phase appears with the highest transition temperature TSG at x = 0.33. The two other magnetic transitions observed for the compounds of x = 0.25, 0.30, 0.33 and 0.40 represent a short range ordered FM state at TM and the second is attributed to a Griffiths phase at TG. Above TG, these samples are also PMI.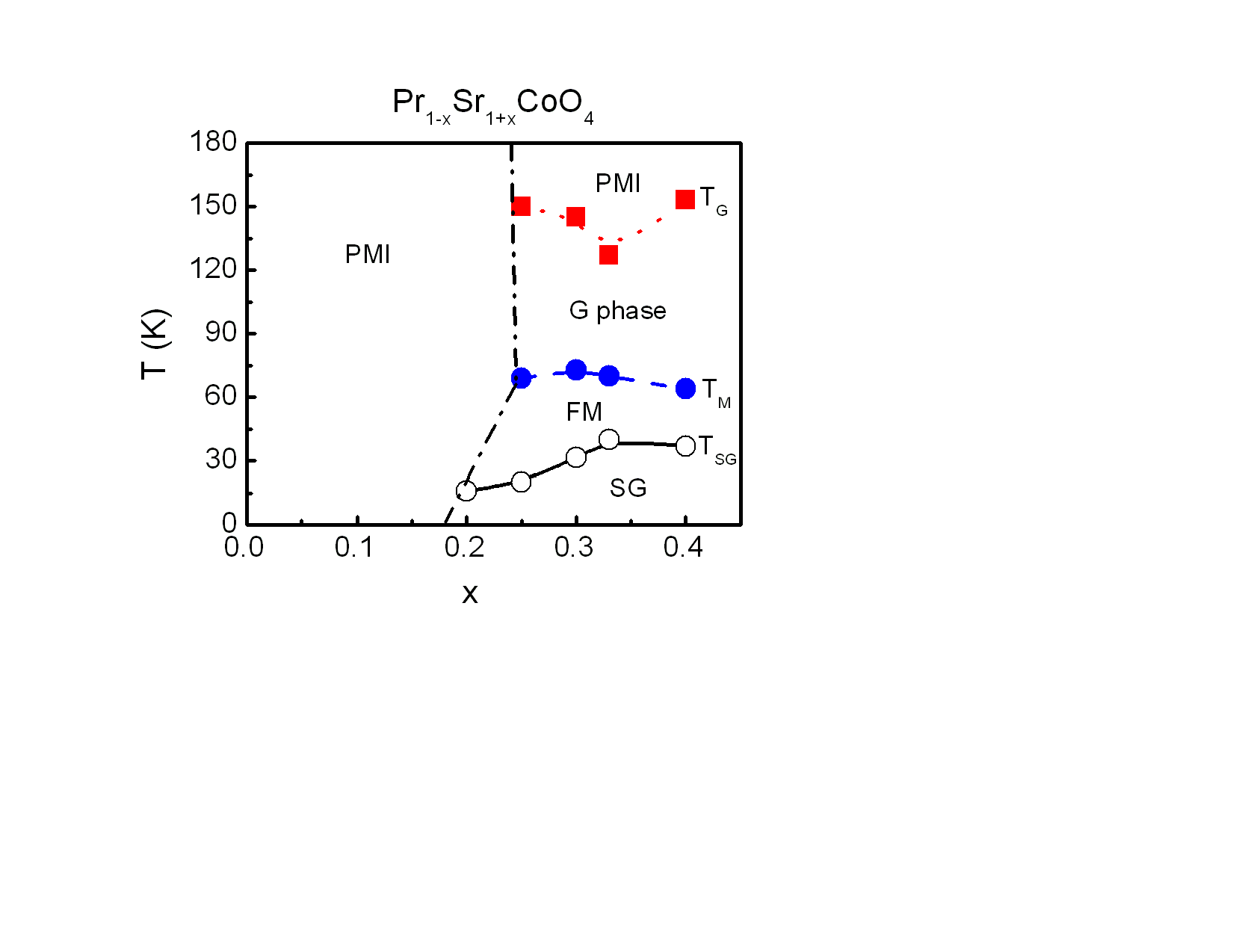 | Figure 9. Phase diagrams for Pr1-xSr1+xCoO4 system. Transition temperatures, TSG, TM and TG determined from magnetic properties are plotted as a function of doping x. The open circles with solid lines represent the spin glass (SG) phase. TM displays the short range ferromagnetic (FM) phase as indicated by red closed circles through dashed lines. Finally, the dotted lines with squares show Griffiths (TG) phase. The states are denoted by abbreviation PMI are paramagnetic insulators. The dash-dotted lines are separation lines between PM and other magnetic transitions |
All samples of Pr1−xSr1+xCoO4 (0 ≤ x ≤ 0.40) crystallize in the K2NiF4 structure with space group I4/mmm. There are strong correlations between the physical properties and the crystal structure of these compounds. The XRD studies show that the unit cell volume increased with the increase of Sr content because the ionic radius of Sr2+ is larger than the ionic radius of Pr3+. The concomitant decrease of the ionic radius of Co by oxidation of Co3+ to Co4+ has a minor effect. The increase of the unit cell volume is mainly caused by an increase of the tetragonal c-axis, whereas the lattice parameter a within the equatorial plane remains almost constant, thereby reflecting the quasi-2D structure of the layered Pr1-xSr1+xCoO4 system. Once again, the parent compound PrSrCoO4 is a paramagnetic semiconductor with strong AFM superexchange interactions evidenced by Tθ = -59.7 K. The octahedral distortion is about 8% which suggests an intermediate S = 1 spin state of the Co3+ ions typically found in these perovskite cobaltates[2]. Upon Sr doping, the oxidation of Co3+ to Co4+ gives rise to FM double exchange. In turn, the Curie-Weiss temperature increases to Tθ = -30.7 K for x = 0.10 reflecting increasing FM double exchange. Meanwhile, the conductivity also increases due to the increasing number of charge carriers and its mobility. Reaching a doping level of x = 0.20, the FM interactions are sufficiently strong that the Curie-Weiss temperature changes sign to Tθ > 0. The competition between FM double exchange and AFM superexchange now leads to a low temperature spin-glass phase (TSG). With increasing applied field this phase is fully suppressed. Because of the decreasing octahedral buckling and distortion, also the AFM superexchange interactions are expected to become stronger according to the Kanamori-Goodenough rules. The electrical conductivity continues to increase from x = 0.10 to x = 0.20. On further increasing the Sr concentration to x = 0.25 and beyond, the interplay between FM double exchange and AFM superexchange is sufficiently strong to give rise to a series of magnetic transitions. Since both types of interactions increase (FM double exchange by the increasing number of Co4+ ions, AFM superexchange by the decrease of the octahedral buckling and distortion), the resulting effect on the magnetic transition temperatures is comparably small. However, for x = 0.25, 0.30, 0.33 a strong change in the electrical transport takes place from a thermal activated behavior to 2D variable range hopping. The charge carrier number and the increased electronic mobility by the double exchange apparently results in a transition from a semiconductor to a quasi-2D metal. Interesting structural and physical changes occur upon increasing the Sr concentration from x = 0.33 to x = 0.40. Structurally, the octahedral distortion significantly increases as shown in the inset of Fig. 2. Based on the analysis of the tolerance factor shown in Fig. 3 and the bond length listed in Table 2, we conclude that a spin state transition takes place from an IS to a HS state of Co3+ ions on going from x = 0.33 to x = 0.40. The crystal structure is now sufficiently large to accommodate high spin Co ions. A high spin state implies strong Hunds coupling and thus on-site interactions. In this sense, an electronic localization is expected as also observed in the homologue La2-xSrxCoO4 compounds[7]. Electronic localization effects are corroborated by the change in the electronic transport back from 2D metallic-like VRH to thermal activation. Localization upon the IS to HS spin state transition is also consistent with the significant increase of the magnetization and hysteresis.
4. Conclusions
We have investigated the structural, magnetic, and electrical properties of Pr1-xSr1+xCoO4 system as a function of doping x and constructed the corresponding phase diagram. While the magnetization of the investigated samples increases with x, the effective paramagnetic magnetic moment decreases slightly because of the dilution of Pr3+ by Sr2+ ions. The substitution of Pr3+ by Sr2+ leads to a volume expansion and the oxidation of Co3+ to Co4+. The latter gives rise to increasing FM double exchange. The interplay of the FM double exchange and AFM superexchange interactions results in a complex magnetic behavior. For the samples of 0.2 ≤ x ≤ 0.4, a spin glass ground state is followed by a short range ordered FM phase and a Griffiths phase before becoming paramagnetic at high temperatures. The electrical conductivity changes from thermally activated semiconducting behavior (x = 0, 0.10, 0.20, 0.40) to 2D-VRH (x = 0.25, 0.30, 0.33). The changes of the magnetic and transport properties correlate with changes in the crystal structure. We found evidence for an IS-HS spin state transition upon doping from x = 0.33 to x = 0.40.
ACKNOWLEDGMENTS
B. G. Kim was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (2011-0006055 and 2011-0006256).
References
| [1] | S. Mukherjee, R. Ranganathan, P. S. Anilkumar and P. A. Joy, Phys. Rev. B 54, 9267 (1996). |
| [2] | K. Knižek, P. Novak, and Z. Jirák, Phys. Rev. B 71, 054420 (2005). |
| [3] | K. Berggold, M. Kriener, C. Zobel, A. Reichl, M. Reuther, R. Müller, A. Freimuth, and T. Lorenz, Phys. Rev. B 72, 155116 (2005). |
| [4] | Y. Furukawa, S. Wada, and Y. Yamada, J. Phys. Soc. Jpn 62, 1127 (1993). |
| [5] | S. Huang, K. Ruan, Z. Lv, L. Zhuang, P. Wei , H. Wu, M. Li, J. Zhang, Y. Chai, H. Yang, L. Cao and X. Li, Phys. Rev. B 73, 094431 (2006). |
| [6] | Y. Moritomo, Y. Tomioka, A. Asamitsu, Y. Tokura and Y. Matsui, Phys. Rev. B 51, 3297 (1995). |
| [7] | N. Sakiyama, I. A. Zaliznyak, S. H. Lee, Y. Mitsui and H. Yoshizawa, Phys. Rev. B 78, 180406(R) (2008). |
| [8] | R. Ang, Y. P. Sun, X. Luo, C. Y. Hao and W. H. Song, J. Phys. D: Appl. Phys. 41, 045404 (2008). |
| [9] | J. Rodriguez-Carvajal, Physica B 192, 55 (1993). |
| [10] | M. Li, S. L. Huang , Z. M. Lv, J. L. Zhang , H. Y. Wu , X. M. Wang, Z. Q. Pang and K. Q. Ruan, Mod. Phys. Lett. B 22, 3195 (2008). |
| [11] | M. Sánchez-Anduĵar and M. A. Señaris-Rodriguez, Solid State Sciences 6, 21 (2004). |
| [12] | Y. Moritomo, K. Higashi, K. Matsuda and A. Nakamura, Phys. Rev. B 55, R14725-R14728 (1997). |
| [13] | S. L. Huang, Z. C. Fan, J. B. Yi, B. C. Zhao, Y. Wu, K. Q. Ruan, M. Li, J. Ding and L. Wang, J. Phys. Cond. Matt. 20, 395213 (2008). |
| [14] | Y. Shimada, S. Miyasaka, R. Kumai and Y. Tokura, Phys. Rev. B 73, 134424 (2006). |
| [15] | Ch. Binek, W. Kleemann and D. P. Belanger, Phys. Rev. B 57, 7791 (1998). |
| [16] | M. Sańchez-Andūjar, B. Rivas-Murias, D. Rinaldi, R. Caciuffo, J. Mira, J. Rivas and M. A. Señaris-Rodriguez, J. Mag. Mag. Mater. 272-276, 855 (2004). |
| [17] | H. Hohl, A. P. Ramirez, T. T. M. Palstra and E. Bucher, J. Alloys Comp. 248, 70 (1997). |
| [18] | A. Hassen, A. I. Ali, B.J. Kim, Y. S. Wu, S. H. Park and Bog. G. Kim, J. Appl. Phys.102, 123905 (2007). |
| [19] | B. I. Shklovskii and A. L. Efros, Electronic Properties of Doped Semiconductors, Springer Series in Solid State Sciences, Vol. 45 (Springer-Verlag), Berlin, Germany. (1984). |
| [20] | N. F. Mott and E. A. Davies, Electronic Processes in Noncrystalline Materials, Oxford Uni- versity Press, Oxford (1979). |
| [21] | I. S. Shlimak, M. J. Lea, P. Fozooni, P. Stefanyi and A. N. Ionov, Phys. Rev. B 48, 11796 (1993). |
| [22] | A. S. Ioselevich, Phys. Rev. Lett. 74, 1411 (1995). |
| [23] | R. Mahendiran and A. K. Raychaudhuri, Phys. Rev. B 54, 16044 (1996). |



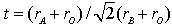 . In the present case, rA represents the average ionic radius of Pr3+ and Sr2+, rB is the mean ionic radius of Co3+ and Co4+ and rO is the ionic radius of O2-. t = 1 corresponds to the ideal cubic perovskite structure. Decreasing values of t < 1 indicate an increasing buckling of the octahedra with a lowering from cubic to tetragonal/orthorhombic symmetry for t < 0.97. For fixed ionic radii, the substitutional series like Pr1−xSr1+xCoO4 necessarily exhibit a linear dependence of the tolerance factor t on concentration, as shown in Fig. 3 for intermediate spin (IS) and high spin (HS) configurations of Co3+, respectively. Similar behavior was observed for La2−xSrx CoO4 system[12]. The ionic radius of Co ions changes depending on their spin state. Taking r(Co3+) = 0.577 Å for the intermediate (IS) spin state and r(Co3+) = 0.61 Å for the high (HS) spin state results in a change from t = 0.962 to 0.952 which fits well with the bond length listed in Table 2. The structural data thus point towards a spin state transition from an IS to a HS sate of Co3+ ions in Pr1-xSr1+xCoO4 on going from x = 0.33 to x = 0.40. The crystal structure is now sufficiently large to accommodate high spin Co ions.
. In the present case, rA represents the average ionic radius of Pr3+ and Sr2+, rB is the mean ionic radius of Co3+ and Co4+ and rO is the ionic radius of O2-. t = 1 corresponds to the ideal cubic perovskite structure. Decreasing values of t < 1 indicate an increasing buckling of the octahedra with a lowering from cubic to tetragonal/orthorhombic symmetry for t < 0.97. For fixed ionic radii, the substitutional series like Pr1−xSr1+xCoO4 necessarily exhibit a linear dependence of the tolerance factor t on concentration, as shown in Fig. 3 for intermediate spin (IS) and high spin (HS) configurations of Co3+, respectively. Similar behavior was observed for La2−xSrx CoO4 system[12]. The ionic radius of Co ions changes depending on their spin state. Taking r(Co3+) = 0.577 Å for the intermediate (IS) spin state and r(Co3+) = 0.61 Å for the high (HS) spin state results in a change from t = 0.962 to 0.952 which fits well with the bond length listed in Table 2. The structural data thus point towards a spin state transition from an IS to a HS sate of Co3+ ions in Pr1-xSr1+xCoO4 on going from x = 0.33 to x = 0.40. The crystal structure is now sufficiently large to accommodate high spin Co ions.


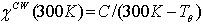 [17, 18] and the contribution of the permanent magnetic moments at room temperature. The differences of the magnetic parameters Tθ and µeff for different applied magnetic fields of 100 Oe and 5000 Oe are small and therefore, only values for H = 5000 Oe are listed in Table 3. As shown in Table 3, χCW(300 K) exhibits an overall increase with increasing Sr content due to increasing magnetic exchange. The effective paramagnetic moment µeff shows only moderate changes upon increasing Sr doping x. The magnetic dilution by substituting rare earth Pr3+ by Sr2+ is, at least to a major part, compensated by an increase of the magnetic moments in the Co sublattice. The presence of the rare earth ions leads to a shift of the effective paramagnetic moments µeff as compared to La1−xSr1+xCoO4 [14].
[17, 18] and the contribution of the permanent magnetic moments at room temperature. The differences of the magnetic parameters Tθ and µeff for different applied magnetic fields of 100 Oe and 5000 Oe are small and therefore, only values for H = 5000 Oe are listed in Table 3. As shown in Table 3, χCW(300 K) exhibits an overall increase with increasing Sr content due to increasing magnetic exchange. The effective paramagnetic moment µeff shows only moderate changes upon increasing Sr doping x. The magnetic dilution by substituting rare earth Pr3+ by Sr2+ is, at least to a major part, compensated by an increase of the magnetic moments in the Co sublattice. The presence of the rare earth ions leads to a shift of the effective paramagnetic moments µeff as compared to La1−xSr1+xCoO4 [14].
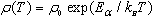


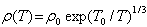
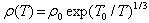
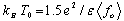 where e is the electronic charge[23].
where e is the electronic charge[23].
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML

