-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Condensed Matter Physics
p-ISSN: 2163-1115 e-ISSN: 2163-1123
2012; 2(4): 88-92
doi: 10.5923/j.ajcmp.20120204.03
A Simple, Potential-Free Model to Calculate Elastic Constants of Solids at High Temperature
Madan Singh 1, Himanshu Narayan 1, Munish Kumar 2
1Department of Physics and Electronics, National University of Lesotho, Roma, 180, Lesotho, Southern Africa
2Department of Physics, G.B. Pant University of Ag. & Technology, Pantnagar, 263145, Uttranchal, India
Correspondence to: Madan Singh , Department of Physics and Electronics, National University of Lesotho, Roma, 180, Lesotho, Southern Africa.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
A simple method for the determination of temperature dependent second order elastic constants (SOEC) of MgO, CaO, Mg2SiO4 and Grossular garnet[Ca3Al2(SiO4)3] using a potential free model based on thermodynamical relationships, has been proposed. The equations developed here are based on the linear relationship between elastic constants at temperatures higher than the Debye temperature. The extrapolated data for elastic constants at very high temperatures obtained in the present study are useful to understand the thermoelastic properties of given solids. It is found that the calculated values of elastic constants, in general, decrease with temperature. The theoretical predictions incorporating the concept of Debye temperature, reported in this paper, are well supported by the available experimental data. The proposed empirical relationship provides a method to estimate the thermoelastic properties of geophysical minerals and solids at high temperature range.
Keywords: Elastic Constants, High Temperature, Thermodynamical Relationships
Article Outline
1. Introduction
- A thorough understanding of the elastic properties of various solids and their variations with temperature is essential in the study of geophysical and geochemical theories of earth interior[1],[2]. Behaviour of minerals under extreme conditions of temperature plays an important role in understanding the dynamics and evolution of lower mantle of earth. Knowledge of elastic constants is essential to interpret the thermodynamic and thermoelastic properties of minerals and solids at high temperatures. The study of temperature dependence of elastic constants for solids has been a subject of wide interest[3],[4]. Therefore, a number of theoretical as well as experimental physicists are currently engaged in the investigations related to elastic constants of diverse materials, employing a wide variety of approaches[5-10]. The elastic constants of some minerals have been calculated starting from the room temperature to higher temperatures, but there are deviations from experimental results after Debye temperature[10-12]. As far as the theoretical studies are concerned, methods like the Monte-Carlo and lattice dynamical simulation using a rigid body model[13] and three-body potential model[14] have been adopted with reasonable amount of success. Nevertheless, there have been some serious weaknesses in these models. For example, in the three-body potential model[14], the short-range overlap potential parameters calculated at 300 K, have been used in the high temperature range as such, presuming to be independent of temperature. Moreover, the Van der Waal’s coefficient calculated from the lattice sums was also taken as temperature independent. The interior separations (r) in various minerals and crystals varies with temperature (Vandana et al[15]) and therefore, it is imperative to consider the short range overlap, as well as the Van der Waal’s interaction parameters, as temperature dependent quantities.In order to overcome the above mentioned discrepancies in existing theories, and to make the theory simpler we have employed a potential free model based on thermodynamical relationships. In this article, we report temperature dependent second order elastic constants (SOEC) of some solids calculated in the higher temperature (
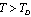 ;
;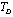 is the Debye temperature)[16] region, using a simple and straightforward theoretical model based on some approximations. This model may be used to calculate the thermoelastic properties of any type of minerals. We have chosen four different crystals, viz., MgO, CaO, Mg2SiO4 and Grossular garnet[Ca3Al2(SiO4)3], to test the outcome of our theory. Among these, MgO and CaO are common oxides, Mg2SiO4 is a material of geophysical importance, and Grossular garnet is a well-known mineral. Basically all these four solids possess cubic crystal structure. However, MgO and CaO have octahedral; Mg2SiO4 has hexoctahedral, and Grossular garnet, dodecahedral coordination geometry. Experimentally determined values of elastic constants for MgO, CaO, Mg2SiO4 and Grossular garnet solids are available in the temperature range starting from 300 K up to 1800 K, 1200 K, 1700 K and 1350 K, respectively[3]. The method of analysis is given in section 2 and results are discussed and compared with experimental data in section 3.
is the Debye temperature)[16] region, using a simple and straightforward theoretical model based on some approximations. This model may be used to calculate the thermoelastic properties of any type of minerals. We have chosen four different crystals, viz., MgO, CaO, Mg2SiO4 and Grossular garnet[Ca3Al2(SiO4)3], to test the outcome of our theory. Among these, MgO and CaO are common oxides, Mg2SiO4 is a material of geophysical importance, and Grossular garnet is a well-known mineral. Basically all these four solids possess cubic crystal structure. However, MgO and CaO have octahedral; Mg2SiO4 has hexoctahedral, and Grossular garnet, dodecahedral coordination geometry. Experimentally determined values of elastic constants for MgO, CaO, Mg2SiO4 and Grossular garnet solids are available in the temperature range starting from 300 K up to 1800 K, 1200 K, 1700 K and 1350 K, respectively[3]. The method of analysis is given in section 2 and results are discussed and compared with experimental data in section 3.2. Method of Analysis
- Starting with the expressions for SOEC[17], as employed on the cubic crystals under isotropic pressure[18]:
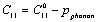 | (1) |
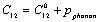 | (2) |
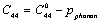 | (3) |
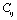 is the SOEC at temperature
is the SOEC at temperature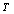 , and
, and 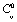 represents their values at 300 K (
represents their values at 300 K (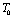 ). The quantity
). The quantity  is phonon pressure, equivalent to the thermal pressure (
is phonon pressure, equivalent to the thermal pressure (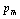 ), which may be evaluated using the following relationship[3],[19],[20]:
), which may be evaluated using the following relationship[3],[19],[20]: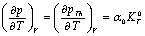 | (4) |
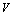 is the volume. Also,
is the volume. Also, 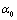 and
and 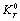 are the coefficient of volume thermal expansion, and bulk modulus, respectively, at
are the coefficient of volume thermal expansion, and bulk modulus, respectively, at 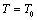 (i.e., at 300 K).One can get the expression for
(i.e., at 300 K).One can get the expression for 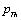 from Eq. 4 as,
from Eq. 4 as,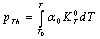 | (5) |
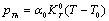 | (6) |
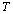 is defined as[19],
is defined as[19],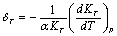 | (7) |
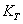 with respect to temperature as,
with respect to temperature as,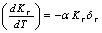 | (8) |
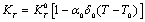 | (9) |
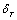 and
and 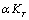 as temperature independent quantities, which has already been assumed empirically in the case of solids studied in[1]. The quantity
as temperature independent quantities, which has already been assumed empirically in the case of solids studied in[1]. The quantity 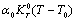 involved in this equation is thermal pressure
involved in this equation is thermal pressure 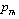 as obtained in Eq. 6 above. Obviously,
as obtained in Eq. 6 above. Obviously, 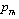 would change with temperature resulting in change in volume. Accordingly, the bulk modulus, as well as other elastic constants, would be temperature dependent. The same inference may also be drawn directly from Eqs. 1-3.Presuming that similar trend of variation with respect to temperature is followed by other elastic constants also; one can generalize Eq. 9[21] to obtain the expressions for the latter, which may be collectively written as:
would change with temperature resulting in change in volume. Accordingly, the bulk modulus, as well as other elastic constants, would be temperature dependent. The same inference may also be drawn directly from Eqs. 1-3.Presuming that similar trend of variation with respect to temperature is followed by other elastic constants also; one can generalize Eq. 9[21] to obtain the expressions for the latter, which may be collectively written as: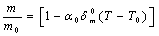 | (10) |
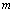 represents any of the elastic moduli such as
represents any of the elastic moduli such as 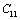 ,
, 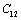 ,
, 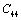 , etc. This expression nicely holds in the
, etc. This expression nicely holds in the 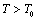 region for the solids whose Debye temperature is near
region for the solids whose Debye temperature is near 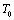 (room-temperature, 300 K), such as the ionic crystals NaCl, KCl, etc.[22]. However, when
(room-temperature, 300 K), such as the ionic crystals NaCl, KCl, etc.[22]. However, when 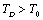 , it holds only up to
, it holds only up to 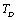 for the calculated values of some SOEC, such as,
for the calculated values of some SOEC, such as, 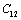 , and then some deviations may occur.Equation 10 therefore, may be modified to accommodate the
, and then some deviations may occur.Equation 10 therefore, may be modified to accommodate the 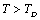 temperature regime by replacing the values of input parameters with those corresponding to
temperature regime by replacing the values of input parameters with those corresponding to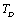 . In the modified picture, the relevant expressions for SOEC at
. In the modified picture, the relevant expressions for SOEC at 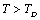 can be collectively written as follows:
can be collectively written as follows: 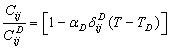 | (11) |
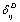 are constants corresponding to
are constants corresponding to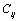 , defined as[23],
, defined as[23],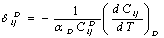 | (12) |
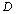 refers to values of the corresponding quantities at Debye temperature,
refers to values of the corresponding quantities at Debye temperature, 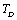 [16].
[16].
|
|
- From this simple theory, taking
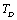 as the reference temperature, one can calculate the values of SOEC that are in excellent agreement with the experimental data. The constants
as the reference temperature, one can calculate the values of SOEC that are in excellent agreement with the experimental data. The constants 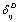 are calculated using Eq. 12 and the input parameter[3] given in Table 1, and then substituted with other quantities in Eq. 11 to obtain the theoretical values of SOEC at different temperatures. The values of
are calculated using Eq. 12 and the input parameter[3] given in Table 1, and then substituted with other quantities in Eq. 11 to obtain the theoretical values of SOEC at different temperatures. The values of 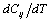 were not available, and therefore, we have used the interpolated values of these quantities at Debye temperature, obtained from the data given in Ref.[3]. These values are listed in Table 1.
were not available, and therefore, we have used the interpolated values of these quantities at Debye temperature, obtained from the data given in Ref.[3]. These values are listed in Table 1.3. Results and Discussion
- Many authors have reported theoretically calculated values of SOEC taking
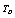 (300 K) as the reference temperature[7],[8]. Therefore, we first calculated all the SOEC values, viz.,
(300 K) as the reference temperature[7],[8]. Therefore, we first calculated all the SOEC values, viz., 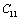 ,
, 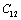 ,
, 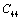 and
and 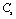 for four different solids MgO, CaO, Mg2SiO4 and Grossular garnet[Ca3Al2(SiO4)3], taking the reference temperature at 300 K instead of
for four different solids MgO, CaO, Mg2SiO4 and Grossular garnet[Ca3Al2(SiO4)3], taking the reference temperature at 300 K instead of 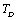 , to understand the inconsistency. To accomplish this, we used room temperature values of the input parameters in Eq. 11. The values of SOEC thus calculated were found to agree to great extent with the available experimental data for all the four solids considered in this work. It was observed that the values of SOEC decrease with increasing T in all four solids, in concurrence with the experimentally reported values, except for the case of
, to understand the inconsistency. To accomplish this, we used room temperature values of the input parameters in Eq. 11. The values of SOEC thus calculated were found to agree to great extent with the available experimental data for all the four solids considered in this work. It was observed that the values of SOEC decrease with increasing T in all four solids, in concurrence with the experimentally reported values, except for the case of 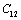 in MgO and CaO. Experimentally, it was observed that for MgO,
in MgO and CaO. Experimentally, it was observed that for MgO, 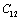 slowly increases with temperature up to 900 K, and then decreases[3]. Mathematically, the slow initial increase of
slowly increases with temperature up to 900 K, and then decreases[3]. Mathematically, the slow initial increase of 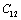 is associated with a positive
is associated with a positive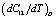 , which is because of a negative value of
, which is because of a negative value of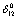 , or vice-verse. At higher temperature (T > 900 K),
, or vice-verse. At higher temperature (T > 900 K), 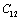 decreased with temperature, which was a reflection of positive
decreased with temperature, which was a reflection of positive 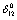 . In the case of CaO, the dependence of
. In the case of CaO, the dependence of 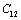 (experimental) on temperature becomes very small, after about 650 K. It may be noted that the change in trend occurs near the respective values of
(experimental) on temperature becomes very small, after about 650 K. It may be noted that the change in trend occurs near the respective values of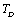 , i.e., 945 K (for MgO) and 671 K (for CaO)[3]. Therefore, the observed change in trend must essentially be associated with
, i.e., 945 K (for MgO) and 671 K (for CaO)[3]. Therefore, the observed change in trend must essentially be associated with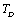 . Like all physical quantities associated with the lattice phonons in solids,
. Like all physical quantities associated with the lattice phonons in solids, 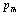 must also change its temperature dependence at
must also change its temperature dependence at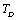 . Effectively, the SOEC that are dependent on
. Effectively, the SOEC that are dependent on 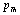 (Eqns. 1-3) should also be expected to change their dependence on temperature beyond
(Eqns. 1-3) should also be expected to change their dependence on temperature beyond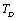 .In order to overcome this discrepancy, we changed the reference temperature from 300 K to the respective Debye temperature
.In order to overcome this discrepancy, we changed the reference temperature from 300 K to the respective Debye temperature 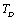 of the solids in Eq. 11, and calculated the SOEC again. Accordingly, the input parameters corresponding to
of the solids in Eq. 11, and calculated the SOEC again. Accordingly, the input parameters corresponding to 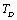 (Table 1) were used in the calculations. Due to the unavailability of experimental SOEC data beyond 1800 K, 1200 K, 1700 K and 1350 K, for MgO, CaO, Mg2SiO4 and Grossular garnet, we calculated the values of elastic constants only up to 1800, 1600, 1700 and 1700 K, respectively, for proper comparison of results.
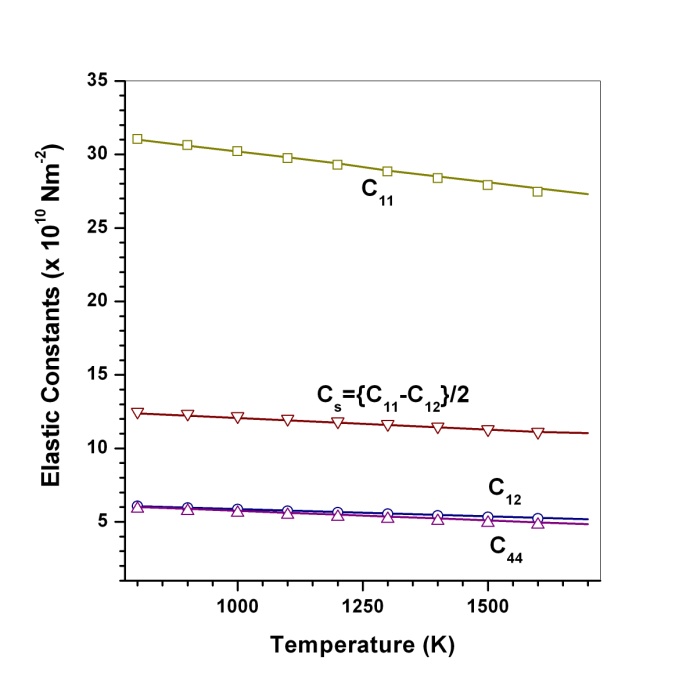
(Table 1) were used in the calculations. Due to the unavailability of experimental SOEC data beyond 1800 K, 1200 K, 1700 K and 1350 K, for MgO, CaO, Mg2SiO4 and Grossular garnet, we calculated the values of elastic constants only up to 1800, 1600, 1700 and 1700 K, respectively, for proper comparison of results. 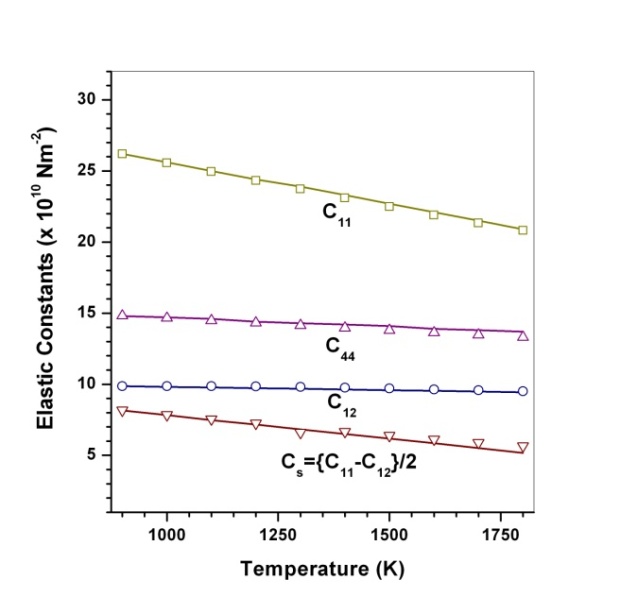 | Figure 1. Variation of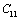 , ,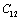 , , 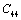 and and 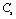 (1010 N/m2) for MgO with temperature. Values calculated in the present study using equation (11) are shown with continuous lines and the experimental data[3], with points (1010 N/m2) for MgO with temperature. Values calculated in the present study using equation (11) are shown with continuous lines and the experimental data[3], with points |
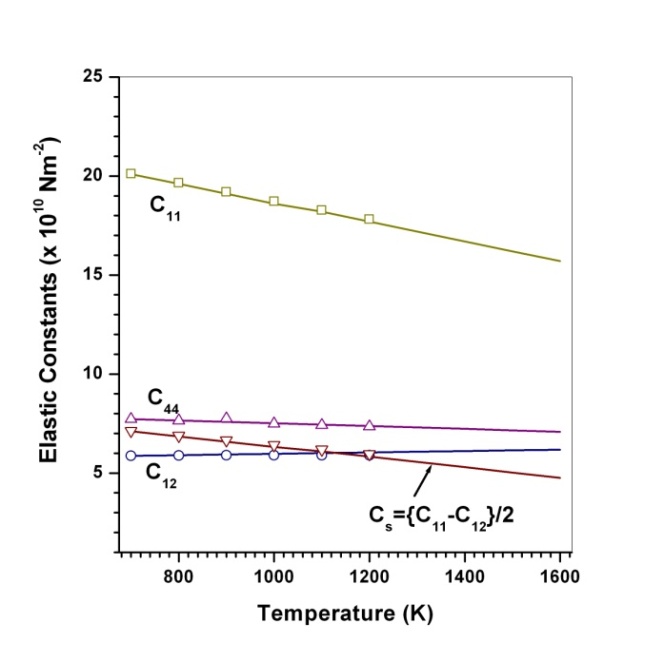 | Figure 2. Variation of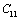 , ,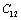 , , 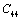 and and 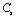 (1010 N/m2) for CaO with temperature. Values calculated in the present study using equation (11) are shown with continuous lines and the experimental data[3], with points (1010 N/m2) for CaO with temperature. Values calculated in the present study using equation (11) are shown with continuous lines and the experimental data[3], with points |
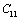 with temperature is found to be large but for
with temperature is found to be large but for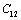 , it is small, and for
, it is small, and for 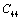 even smaller. This is because the constant
even smaller. This is because the constant 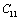 represents elasticity in length, and a longitudinal strain produces a change in volume without any change in shape. The volume change is closely related to temperature and therefore, produces a large change in
represents elasticity in length, and a longitudinal strain produces a change in volume without any change in shape. The volume change is closely related to temperature and therefore, produces a large change in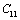 . On the other hand,
. On the other hand, 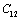 and
and 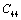 are related to elasticity in shape without the change in volume, which makes
are related to elasticity in shape without the change in volume, which makes 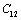 and
and 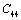 less temperature sensitive. Variations of the elastic constants
less temperature sensitive. Variations of the elastic constants 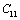 ,
, 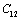 ,
, 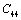 and
and 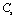 with temperature, for
with temperature, for 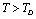 , calculated using
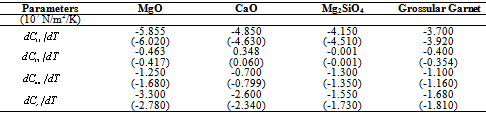
, calculated using 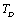 as the reference temperature, are shown in Figs. 1-4 for the MgO, CaO, Mg2SiO4 and Grossular garnet, respectively. For comparison, the experimentally determined values of the corresponding elastic constants are also shown. It may easily be noted that the calculated values, in general, are in very good agreement with the available experimental data[3]. This observation has been consolidated with the estimation of slopes of each of the theoretical lines, as well as that of the best fitting straight lines to experimental data. Values of these slopes, which essentially represent the rate with which a given SOEC varies with respect to temperature, are listed in Table 2. A comparison between theoretical, and the corresponding experimental, values of the slopes immediately reveals the significant agreement between the two. Moreover, since
as the reference temperature, are shown in Figs. 1-4 for the MgO, CaO, Mg2SiO4 and Grossular garnet, respectively. For comparison, the experimentally determined values of the corresponding elastic constants are also shown. It may easily be noted that the calculated values, in general, are in very good agreement with the available experimental data[3]. This observation has been consolidated with the estimation of slopes of each of the theoretical lines, as well as that of the best fitting straight lines to experimental data. Values of these slopes, which essentially represent the rate with which a given SOEC varies with respect to temperature, are listed in Table 2. A comparison between theoretical, and the corresponding experimental, values of the slopes immediately reveals the significant agreement between the two. Moreover, since 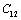 is a monotonically decreasing function of temperature (Eq. 11), when the reference temperature is set at
is a monotonically decreasing function of temperature (Eq. 11), when the reference temperature is set at 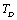 , as we have done in our calculations, the theory is expected to agree with the experimental data even up to the melting temperature of the solid under consideration.Finally, so far as the validity of theory in the temperature regime
, as we have done in our calculations, the theory is expected to agree with the experimental data even up to the melting temperature of the solid under consideration.Finally, so far as the validity of theory in the temperature regime 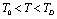 is concerned, values obtained with
is concerned, values obtained with 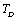 as the reference temperature are better than those obtained with
as the reference temperature are better than those obtained with 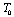 as the reference. This is evidenced from the fact that the maximum observed difference in theoretical and experimental values of
as the reference. This is evidenced from the fact that the maximum observed difference in theoretical and experimental values of 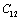 for MgO and CaO, are larger with the latter reference temperature. Therefore, it can be concluded that the theory reported here is valid at higher temperatures, especially beyond the Debye temperature.
for MgO and CaO, are larger with the latter reference temperature. Therefore, it can be concluded that the theory reported here is valid at higher temperatures, especially beyond the Debye temperature.4. Conclusions
- The Variation of SOEC of solids has been investigated on the basis of Anderson equation[19] with first order approximations. Good conformity between calculated and experimental values of SOEC from Debye temperature to higher temperature for solids under study reveals the validity of relationships used in the present analysis. The simple method developed in the present work is free from the theory of potential, and the results obtained are in good agreement with complete simulation studies as well. On the basis of overall descriptions, the method was found to be better than those reported earlier[10],[12], as far as the simplicity and applicability are concerned. The approach is independent of crystal structure and may be extended to the more complex solids like minerals of geophysical importance up-to their respective melting temperature. Due to the simplicity of calculations and potentially wider applicability, this model might be used in calculating the thermoelastic properties of various nanomaterials[24],[25]. More work in this direction is in progress.
ACKNOWLEDGEMENTS
- The authors are thankful to the referee for his valuable comments, which have been useful in revising the manuscript.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML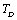 and the input parameters (near
and the input parameters (near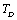 ) used in calculations[3]
) used in calculations[3] 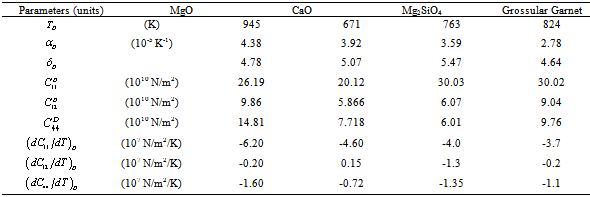
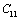 ,
,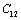 ,
, 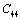 and
and 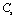 (1010 N/m2) for Mg2SiO4 with temperature. Values calculated in the present study using equation (11) are shown with continuous lines and the experimental data[3], with points
(1010 N/m2) for Mg2SiO4 with temperature. Values calculated in the present study using equation (11) are shown with continuous lines and the experimental data[3], with points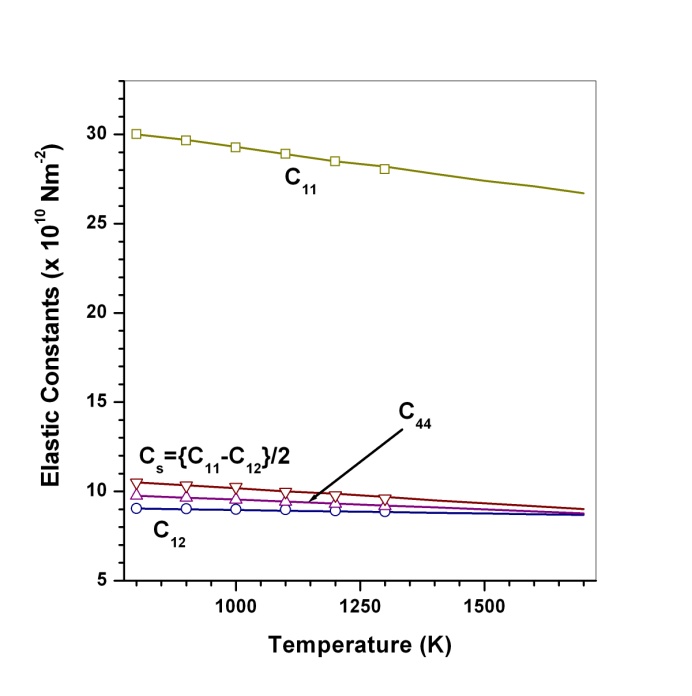
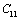 ,
,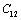 ,
, 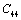 and
and 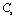 (1010 N/m2) for Grassular garnet with temperature. Values calculated in the present study using equation (11) are shown with continuous lines and the experimental data[3], with points
(1010 N/m2) for Grassular garnet with temperature. Values calculated in the present study using equation (11) are shown with continuous lines and the experimental data[3], with points