1. Introduction

Aluminium arsenide (AlAs) is a compound semiconductor with an indirect band gap and it has a zinc-blend (zb) structure[1]. AlAs is the most technologically important compound semiconductor material, where it has many optoelectronics and photovoltaic applications in space solar cells, telecommunication and data communication networks, mobiles, telephones, laptop computers, compact disc players, etc[2]. Therefore, aluminium arsenide has been intensively investigated in the recent years, where Bouarissa and Boucenna[3] studied the electronic, optical and mechanical properties of AlAs and they showed that the results are in agreement with the available experimental and theoretical data. Chimata[4] studied theoretically the electronic structure of aluminium arsenide crystal, and they found that the band gap value obtained is in good agreement with the experimental value. Shimazaki and Asai[5] studied the energy band structure of Si, AlP, AlAs, GaP and GaAs using screened Hartree–Fock exchange method, and they found that the direct and indirect band gaps don't agree with experimental values.

The aforementioned researches and most of other researches deal with bulk AlAs crystals. Due to our extended literature survey, it is found that the electronic properties of AlAs nanocrystals are not investigated comprehensively. Sothe aim of the present work is to achieve this task. In the present work we introduce the ab-initio restricted Hartree-Fock(RHF) formalism within the frame of large unit cell (LUC) method to investigate the electronic structure of AlAs nanocrystals (nc_s) employing Gaussian (03) software[6] to perform the calculations. This method has been chosen in the present work rather than other methods because this method is very reliable to analyse the electronic properties of solids, and because of the significant advantage of ab-initio methods which is the ability to study reactions that involve breaking or formation of covalent bonds, which correspond to multiple electronic states. The downside of ab-initio methods is their computational cost. They often take enormous amounts of computer time, memory and disk space[7].

2. Theory

The main idea of the large unit cell is computing the electronic structure of the unit cell extended in a special manner at k=0 in the reduced Brillouin zone[8, 9]. Using the linear combination of atomic orbitals (LCAO), the crystal wavefunction in the (LUC-RHF) formalism is written in the following form[10, 11]:

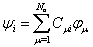(1)

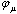where ψ_i is the molecular orbital, C_μi are the molecular orbital expansion coefficients, is the atomic orbital, N₀ is the number of the atomic orbitals. The total electronic energy can be written as[12, 13, 14]:

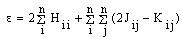(2)

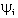where H_ii is the expectation value of the one electron core Hamiltonian corresponding to the molecular orbital (), J_ij and K_ij are the Coulomb and exchange operators respectively, and they are expressed as follows:

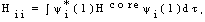(3)

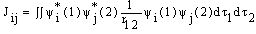(4)

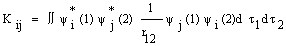(5)

Substituting the linear expansion of Eq.(1) in the molecular orbital integrals, yields:

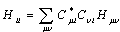(6)

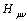where is the core Hamiltonian matrix elements,

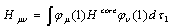(7)

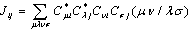(8)

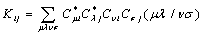(9)

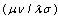where is the differential overlap matrix elements,

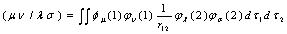(10)

The total electronic energy of Eq.(2) can be written in terms of integral over atomic orbitals. By substituting the previous expressions in the equation of the electronic energy, one can obtain

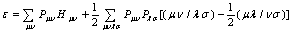(11)

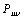where is the density matrix elements,

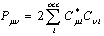(12)

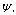The summation is over occupied orbitals only for closed shell systems which is the case in the present work. Applying the variational method to Eq.(11), a small variation of the molecular orbital can now be given as:

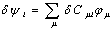(13)

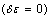And when the condition for a stationary point is applied, one can obtain the following final form[15,16]:

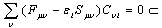(14)

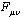where is the Fock matrix,

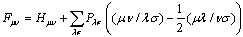(15)

3. Results and Discussion

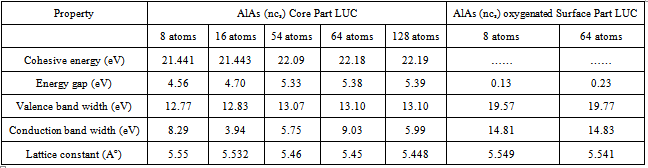
In the present work we have used Gaussian (3) software to calculate the lattice constant, energy gap, cohesive energy, valence band width and degeneracy of states of AlAs nc_s (core and surface). These properties are illustrated in table (1) and they are compared with other experimental and theoretical results in table (2). We divided the work into two parts, core and surface parts. In the core part we chose the number of atoms (8, 16, 54, 64, 128) for the (LUC), while in the surface part the choice of number of atoms is (8 and 64) because these numbers of atoms give cubic shapes.

The calculated total energy of AlAs nc_s as a function of lattice constant for the LUC of (8) atoms is shown in Fig. (1). The equilibrium lattice constant is at the minimum of the total energy curve.

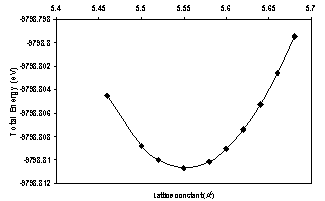Figure 1. Total energy as a function of lattice constant for 8 atom (core) LUC

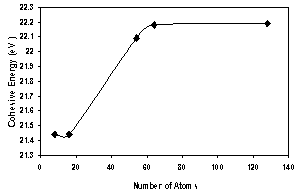Figure 2. Cohesive energy as a function of number of atoms for AlAs (ncs)

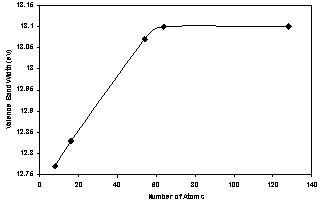Figure 3. The valence band width as a function of number of atoms for AlAs (ncs)

From Fig. (1), it is shown that the total energy in the core part decreases with increasing the lattice constant till it reaches the equilibrium lattice constant. After the equilibrium lattice constant, the total energy increases with the increase of lattice constant. The behaviour of the total energy as a function of the lattice constant is due to the attraction forces that take place at the large distances between atoms. Decreasing the distance between atoms leads to decreasing the total energy. At shorter distances between atoms, the repulsion forces become dominant and take place to cause the increase of the total energy. The stability of the nanocrystal at the equilibrium lattice constant is due to the equality of the attraction and repulsion forces at this point. In the surface part, we show that the total energy has the same behaviour as that of the core with less values of the total energy of the surface compared with that of the core. The decrease of the total energy for surface is caused by broken bonds and discontinuity at the surface leading to decrease in lattice constant. Also we show that the cohesive energy and valence band width increase with increasing the number of atoms per (LUC), reaching to 64 atoms in which they tend to stabilize, with the increasing number of atoms as shown in Fig. (2) and Fig. (3) respectively. The energy gap increases with increasing the number of atoms for core as in Fig. (4). Also the energy gap of oxygenated(001)-(1×1) surface increases with increasing the number of atoms. The conduction band width has some fluctuations.

An interesting observation can be deduced from Table (2), which is the significant difference between the electronic properties of AlAs nanocrystals compared with the corresponding properties of bulk AlAs crystal.

The cohesive energy of AlAs (nc_s) has high value in comparison with the experimental and theoretical values. Many factors that affect the cohesive energy are not introduced in the present calculations that include: correlation corrections, relativistic corrections, in addition of Simple STO-3G basis is used in the present work to be able to reach higher number of core and surface atoms. The present value of the cohesive energy and other properties can be greatly enhanced by merely changing the simple STO-3G basis used in the present calculations to a more sophisticated basis states. However, more sophisticated basis states consume more memory and computer time and will eventually prevent us from reaching large number of atoms. The high value of the band gap can be attributed to the approximations involved in HF method as well as in the present RHF-LUC formalism. and due to bonds nature (mixed bonds) in AlAs (nc_s), this sometimes causes very large band gaps for these nanocrystals[21].

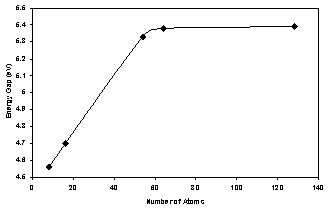Figure 4. Energy gap as a function of number of atoms for AlAs( ncs)

Table 1. The electronic structure of AlAs (ncs)

Table 2. Electronic structure of AlAs (ncs) of the present work compared with theoretical and bulk experimental values Property Present work (8 atoms LUC) Theor.(Bulk) Exp. (Bulk) Cohesive energy (eV) 22.975 8.89[17] 8.00[17] Energy gap (eV) 4.56 2.32[18] 2.25[18] Valence band width (eV) 12.77 11.37[19], 11.89[20] …… Conduction band width (eV) 8.29 …… …… Lattice constant (Ao) 5.55 5.70[18] 5.65[18]

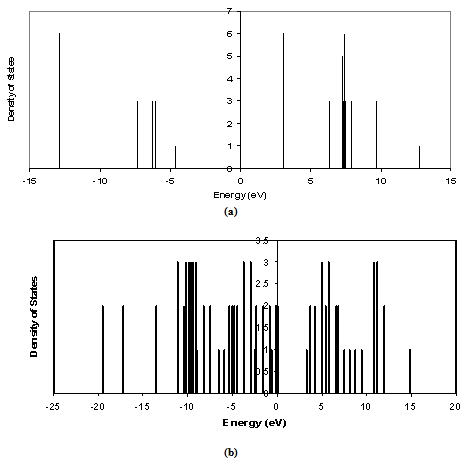Figure 5. Density of states as a function of energy levels for 8 atoms LUC: (a) core, and (b) oxygenated (001)-(1×1) slab

The density of states of AlAs (nc_s) as a function of the energy levels was calculated for both core and surface parts. Fig. (5a) shows the density of states for (8) atoms core LUC and Fig. (5b) represents the density of states for oxygenated (001)-(1×1) AlAs (nc_s) surface. The difference of the degeneracy of the surface in comparison with that of the core is caused by the broken bonds and the discontinuity at the surface and the existence of new kind of atoms (oxygen atoms) that leads to varying the bond lengths and angles, and then to changing the geometry of the structure.

4. Conclusions

1. The present work reveals an interesting fact that the electronic structure of AlAs nanocrystals differs significantly from that of the bulk AlAs crystal.

2. The present method cannot be used only to investigate the electronic properties of bulk crystals, but it may be also used to investigate the electronic properties of nanocrystals.

3. The lattice constant of all size of AlAs nc_s (core and surface) decreases with increasing the number of atoms in the LUC.

4. The present calculations show that the energy gap and valence band (absolute value) increase as the AlAs (nc_s) LUC size increases for both the core and oxygenated (001)-(1×1) surface. Also the cohesive energy (absolute value) for the core part increase with increasing the number of atoms.

5. The energy gap is controlled by the surface part of the nanocrystal. The surface part has lower symmetry than the core part with smaller energy gap and wider valence band. The density of states of the core part is higher than that of the surface part. This reflects the high symmetry and equal bond lengths and angles in the perfect AlAs nanocrystals structure.