Vladimir Mukhomorov
Agrophysical Institute, St-Petersburg, 195220, Russia
Correspondence to: Vladimir Mukhomorov , Agrophysical Institute, St-Petersburg, 195220, Russia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
A theoretical analysis of a homogeneous magnetic field the action on the electronic terms of the bipolaron in the triplet 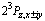 state is made. It is shown that the action of the magnetic field, on the one hand, leads to displacement of the triplet terms to the low-energy region and thus to stabilization of the bipolaron and, on the other hand, appreciable weakens the criteria that limit the conditions of their existence. It is shown that the inclusion of electron-electron correlation leads to the stabilization of the triplet bipolaron, as well as to expand the boundaries of his existence.
state is made. It is shown that the action of the magnetic field, on the one hand, leads to displacement of the triplet terms to the low-energy region and thus to stabilization of the bipolaron and, on the other hand, appreciable weakens the criteria that limit the conditions of their existence. It is shown that the inclusion of electron-electron correlation leads to the stabilization of the triplet bipolaron, as well as to expand the boundaries of his existence.
Keywords:
Bipolaron, Polaron, Singlet, Triplet, Magnetic Field, Interelectron Correlations
1. Introduction
It was postulated previously[1] the possibility of the existence in polar media of a bound two polarons (bipolaron) formations in a triplet (23P) state whose structure resembles the helium atom in the excited 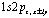 state. Such two polarons species can be formed in polar media where autolocalization is associated with the formation of a fairly deep and wide polarization potential well. It was shown that polarons can exist in the ground and relaxation-excited states. As is well known[2], optical excitation of a polaron Franck-Condon transition occurs between the electronic 1s and
state. Such two polarons species can be formed in polar media where autolocalization is associated with the formation of a fairly deep and wide polarization potential well. It was shown that polarons can exist in the ground and relaxation-excited states. As is well known[2], optical excitation of a polaron Franck-Condon transition occurs between the electronic 1s and 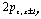 - states, the oscillator strength is ~ 0.9. At the same time the possible existence of singlet axially- symmetrical bipolarons has been widely discussed[3-10]. The most probable dipole-actives the optical transition for ground state of Landau-Pekar bipolaron will be
- states, the oscillator strength is ~ 0.9. At the same time the possible existence of singlet axially- symmetrical bipolarons has been widely discussed[3-10]. The most probable dipole-actives the optical transition for ground state of Landau-Pekar bipolaron will be 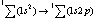 . For the special case
. For the special case 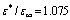 (a polaron in ammonia), we obtain the transition frequency
(a polaron in ammonia), we obtain the transition frequency 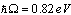 , which is very close to the experimental value 0.81eV[10].The bipolarons in triplet state will have an anomalous chemical activity and, in view of the translational invariance of the system, can transfer the trapped energy quantum in a selected direction. The spin prohibition of the emission of a photon from a metastable state is lifted as a result of relativistic interactions, but this deactivation mechanism is inefficient. Also possible are T→S (triplet→singlet) transition due to the interaction of the electron spin with the transverse phonons of the polar media. They lead to a change in the spatial symmetry of the bipolaron. From a centrally symetric state it changes to a singlet quasi-molecular bipolaron. However, in view of the small magnitude of the magnetic interactions, the spontaneous T→S transitions are of low probability. Triplet bipolarons may be treated as active centers having an inverted population relative to the ground singlet state.It is known[11] that a magnetic field lowers the energy of a polarons and stabilizes the relaxation-excited states relative to the processes of nonradiative deactivation. The present paper analyzes the conditions of triplet bipolarons existence and the effect of a magnetic field on the energy terms bipolaron in triplet state.
, which is very close to the experimental value 0.81eV[10].The bipolarons in triplet state will have an anomalous chemical activity and, in view of the translational invariance of the system, can transfer the trapped energy quantum in a selected direction. The spin prohibition of the emission of a photon from a metastable state is lifted as a result of relativistic interactions, but this deactivation mechanism is inefficient. Also possible are T→S (triplet→singlet) transition due to the interaction of the electron spin with the transverse phonons of the polar media. They lead to a change in the spatial symmetry of the bipolaron. From a centrally symetric state it changes to a singlet quasi-molecular bipolaron. However, in view of the small magnitude of the magnetic interactions, the spontaneous T→S transitions are of low probability. Triplet bipolarons may be treated as active centers having an inverted population relative to the ground singlet state.It is known[11] that a magnetic field lowers the energy of a polarons and stabilizes the relaxation-excited states relative to the processes of nonradiative deactivation. The present paper analyzes the conditions of triplet bipolarons existence and the effect of a magnetic field on the energy terms bipolaron in triplet state.
2. Basic Equations and Mathematical Method
In the adiabatic approximation the wave function of the system, the electron and the field of longitudinal long- wavelength phonons of polar medium can be described as the product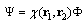 | (1) |
of a two-electron wave function 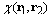 and a wave function
and a wave function 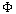 of normal vibrations of a dielectric continuum. To determine the energy of the two polarons system it is necessary to minimize the functional
of normal vibrations of a dielectric continuum. To determine the energy of the two polarons system it is necessary to minimize the functional 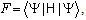 | (2) |
under the additional conditions 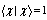 and
and 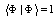 ; to describe the behavior of electrons in a polarizing medium we use the generalized Hamiltonian
; to describe the behavior of electrons in a polarizing medium we use the generalized Hamiltonian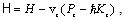 | (3) |
where Pz is the component of the total momentum operator, Kz is its eigenvalue, and vg is the mean translation velocity of the polaron moving along the z axis, 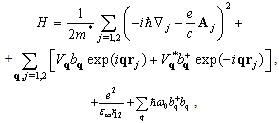 | (4) |
where rj is the radius vector of the jth electrons; bq and bq+ are the Bose operators of annihilation and creation of a quantum of longitudinal phonons with quasi-momentum 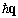 and longitudinal eigenfrequency ω0 (q = 0); and the Fourier coefficients
and longitudinal eigenfrequency ω0 (q = 0); and the Fourier coefficients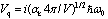
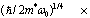
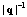 characterize the interaction of the electron with the polarization continuum. The dimensionless coupling constant is
characterize the interaction of the electron with the polarization continuum. The dimensionless coupling constant is 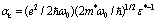 , m* is the effective electron mass in the approximation of the isotropic and quadratic law of dispersion, and V is the volume of the main region of the continuum. The effective permittivity is
, m* is the effective electron mass in the approximation of the isotropic and quadratic law of dispersion, and V is the volume of the main region of the continuum. The effective permittivity is 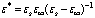 ,
, 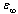 and
and 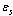 are the high-frequency and static permittivities of the polar medium. The vector potential of a constant homogeneous magnetic field directed along the z axis will be chosen in the symmetric form
are the high-frequency and static permittivities of the polar medium. The vector potential of a constant homogeneous magnetic field directed along the z axis will be chosen in the symmetric form 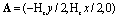 .Varying Eq. (2) with respect to and allowing for Eqs. (1) and (3), we obtain the following equation for the eigenvalues for the polarization continuum:
.Varying Eq. (2) with respect to and allowing for Eqs. (1) and (3), we obtain the following equation for the eigenvalues for the polarization continuum: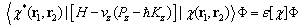 | (5) |
The left-hand side of Eq. (5) can be rewritten as follows: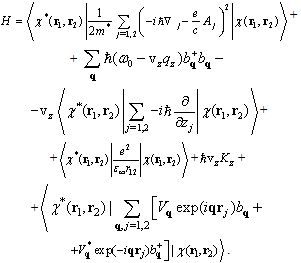 | (6) |
We introduce the unitary transformation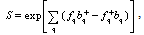 | (7) |
which converts Eq. (6) to a diagonal form.The unknown functions fq and fq* are determined from the condition of minimum of the functional S+HS. Considering the operator identities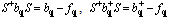 we obtain
we obtain 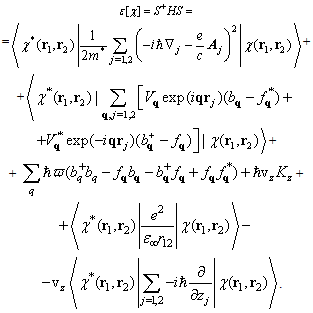 | (8) |
Varying Eq. (8) with respect to fq and fq* , we find the unknown functions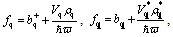 | (9) |
where 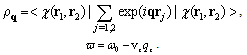 Substituting Eq.(9) into Eq.(8) we obtain the total energy functional, which takes into account the translational displacement of the bipolaron as a whole
Substituting Eq.(9) into Eq.(8) we obtain the total energy functional, which takes into account the translational displacement of the bipolaron as a whole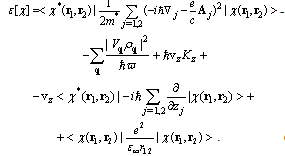 | (10) |
Considering the cylindrical symmetry of the problem, for slow velocity 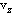 the electronic part of the wave function will be written in the form
the electronic part of the wave function will be written in the form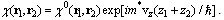 | (11) |
Substituting Eq. (11) into Eq.(10), we obtain the following equation for total energy of two-polaron system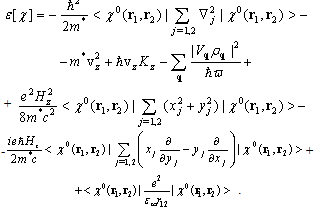 | (12) |
Assuming that 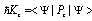 , as well as the definitions Eqs.(1) and (11), for the eigenvalue of the momentum operator, we find
, as well as the definitions Eqs.(1) and (11), for the eigenvalue of the momentum operator, we find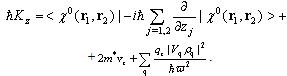 | (13) |
Substituting Eq. (13) into Eq. (12), we can readily obtain a general expression for the total energy of a bipolaron in a magnetic field allowing for its translational displacement: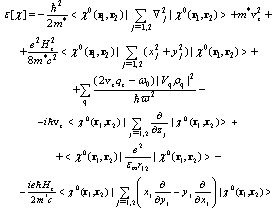 | (14) |
We expand 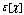 in power of
in power of 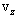 and keeping only the quadratic terms in the series, obtain
and keeping only the quadratic terms in the series, obtain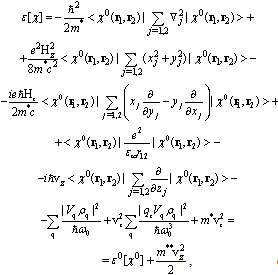 | (15) |
where the longitudinal translational mass of the bipolaron is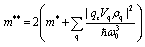 | (16) |
Thus, for slow velocities, the energy of translational motion can be separated from the intrinsic energy of the polaron. This makes it possible to consider  separately in Eq. (15). It is convenient henceforth to change from the q representation in Eq. (15) to a coordinate representation, and to introduce the one-electron spinless density function, which in the general case of an N-electron system may be written
separately in Eq. (15). It is convenient henceforth to change from the q representation in Eq. (15) to a coordinate representation, and to introduce the one-electron spinless density function, which in the general case of an N-electron system may be written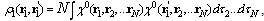 | (17) |
with 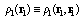 , and the two-electron spinless density function is
, and the two-electron spinless density function is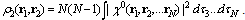 | (18) |
Then the self-consistent total energy of the stationary bipolaron formation may be written as follows: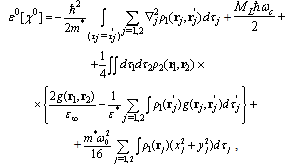 | (19) |
where ML is the projection of the orbital angular momentum L on the selected axis z, the cyclotron frequency is 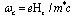 , the electron-electron interaction operator is
, the electron-electron interaction operator is 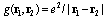 , and the energy is reckoned from the bottom of the conduction band at Hz = 0. In the derivation of Eq. (19), the identity
, and the energy is reckoned from the bottom of the conduction band at Hz = 0. In the derivation of Eq. (19), the identity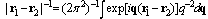 was considered, and the operator transformations of Ref. [12] were used.We shall consider triplet singly excited electronic states (for distances R → ∞ the energy of the two polaron system corresponds to the
was considered, and the operator transformations of Ref. [12] were used.We shall consider triplet singly excited electronic states (for distances R → ∞ the energy of the two polaron system corresponds to the 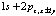 configuration).
configuration). 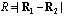 is the distance between centers of polarons gravity [1,9], while the vector ri is associated with oscillation motion of electron in polarization potential well near Ri. The two-electron wave function of the electronic excited state, approximating the eigenfunction
is the distance between centers of polarons gravity [1,9], while the vector ri is associated with oscillation motion of electron in polarization potential well near Ri. The two-electron wave function of the electronic excited state, approximating the eigenfunction 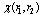 should be antisymmetric with respect to the transposition of both electrons orthogonal to the ground state. In the approximation of quasi-independent electrons, the electronic part of the two-center wave function (the centers of the potential wells are found at points a and b, separated by distance R) will be written in the Heitler-London form
should be antisymmetric with respect to the transposition of both electrons orthogonal to the ground state. In the approximation of quasi-independent electrons, the electronic part of the two-center wave function (the centers of the potential wells are found at points a and b, separated by distance R) will be written in the Heitler-London form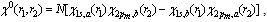 | (20) |
where N is the normalization constant. Subscripts a and b refer to polarons located at R1 and R2, respectively. χ1s and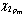 are one-particle wave functions of the 1s and 2pm states, and m = z, x±iy. The coordinate one-particle wave functions are chosen in the form of orthonormalized two-parameter Gaussian-type functions
are one-particle wave functions of the 1s and 2pm states, and m = z, x±iy. The coordinate one-particle wave functions are chosen in the form of orthonormalized two-parameter Gaussian-type functions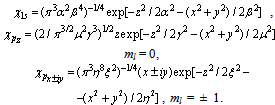 | (21) |
The minimization of Eq. (19) must be carried out with respect to the parameters α, β, γ, μ, ξ and η for fixed values of R and ε*/ε∞ . The magnetic field removes the degeneracy with respect to the magnetic quantum number ML of bipolaron, and the total energy Eq. (19) for the states 23Pz(ML = 0) and 23Px±iy(ML = ± 1) may be written in the form 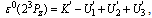 | (22) |
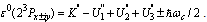 | (23) |
The variational parameters can be found only numerically, and in the selfconsistent state the virial theorem should be satisfied. We introduce the scale transformation r → tr, R → tR, χ(r) → t3/2χ(tr) and then obtain for the function of the total energy (without magnetic field)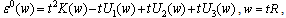 | (24) |
where K is the mean kinetic energy of electrons, U1 is the mean energy of interaction between electrons exchanging phonons, U2 is diamagnetic part of the energy, and the mean Coulomb interaction energy of electrons is U3. Minimizing Eq. (22) with respect to t and assuming t = 1, we obtain the virial relation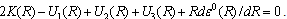 | (25) |
The virial relation Eq.(25) should be satisfied for all interpolaron distances.The triplet bipolaron in 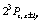 state will be stable to adiabatic dissociation by two polarons with conservation of the total spin and orbital angular momentum if the binding energy
state will be stable to adiabatic dissociation by two polarons with conservation of the total spin and orbital angular momentum if the binding energy 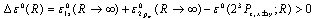 where
where 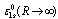 and
and 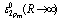 are the self-consistent total energy of the polarons in 1s and 2pm states. Figure 1 shows the total energy of the bipolaron on the distance R for dielectric parameters
are the self-consistent total energy of the polarons in 1s and 2pm states. Figure 1 shows the total energy of the bipolaron on the distance R for dielectric parameters 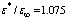 . Triplet bipolaron has minima when R = 0. For R = 0 in extreme case
. Triplet bipolaron has minima when R = 0. For R = 0 in extreme case 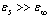 the ratio
the ratio 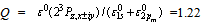 . With a decrease in the value of Q ratio decreases and reaches unity at
. With a decrease in the value of Q ratio decreases and reaches unity at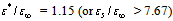 .Let us consider the change in the total energy of the triplet bipolaron in the limit of a weak magnetic field:
.Let us consider the change in the total energy of the triplet bipolaron in the limit of a weak magnetic field: 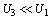 . In this case, we assume that the bipolaron has central symmetry (
. In this case, we assume that the bipolaron has central symmetry (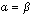 and
and 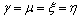 ). Hence, to determine the energy change, use may be made of the methods of perturbation theory, which for the 23Pz state gives the energy correction
). Hence, to determine the energy change, use may be made of the methods of perturbation theory, which for the 23Pz state gives the energy correction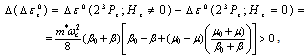 | (26) |
since 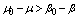 and
and 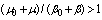 [10] it is evident that in the presence of a magnetic field
[10] it is evident that in the presence of a magnetic field 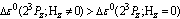 , i.e., the term of the total energy of the triplet bipolaron becomes lower, and is stabilization takes place.
, i.e., the term of the total energy of the triplet bipolaron becomes lower, and is stabilization takes place. 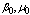 and
and 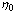 are the parameters for Hz = 0. The corresponding inequality can also be written for
are the parameters for Hz = 0. The corresponding inequality can also be written for 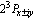 term:
term: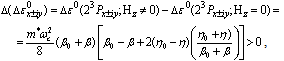 | (27) |
since 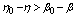 and
and 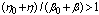 . In magnetic fields (dimensionless)
. In magnetic fields (dimensionless) 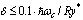 , where
, where 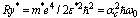 , the change in coupling energy for states with ML = 0 and ML = ± 1 is different, and independently of the ratio of the permittivities of the medium, always
, the change in coupling energy for states with ML = 0 and ML = ± 1 is different, and independently of the ratio of the permittivities of the medium, always 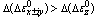 . However, in magnetic fields:
. However, in magnetic fields: 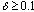 , the energy change of the 23Pz term becomes more significant than that of the 23Px±iy term, and for polar media with a smaller ratio of
, the energy change of the 23Pz term becomes more significant than that of the 23Px±iy term, and for polar media with a smaller ratio of 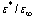 , this shift takes place in lower fields.
, this shift takes place in lower fields. | Figure 1. Triplet terms of the bipolaron as function of the polaron-polaron distance. 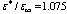 |
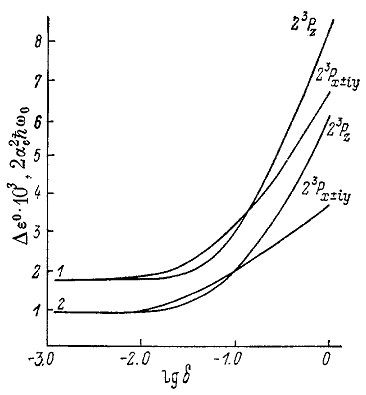 | Figure 2. The binding energy of the triplet bipolaron as function of the magnetic field (dimensionless). 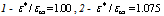 |
In the range of magnetic field values for which U1 > U3, i.e., 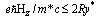 , a variation calculation of the change in total energy terms is shown in Fig.2 for two cases:
, a variation calculation of the change in total energy terms is shown in Fig.2 for two cases: 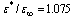 and extreme ratio
and extreme ratio 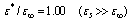 . These results fully confirm the conclusions that follow from Eqs. (26) and (27). Irrespective of the permittivity ratio, a constant homogeneous magnetic field decreases the energy of the triplet bipolaron, and this in turn leads to stabilization of bipolarons with respect to dissociative decay. Moreover, the action of the magnetic field expands the range of dielectric media where bound two-polaron formation can exist. Thus for the 23Pz state, even in a dimensionless field as low as
. These results fully confirm the conclusions that follow from Eqs. (26) and (27). Irrespective of the permittivity ratio, a constant homogeneous magnetic field decreases the energy of the triplet bipolaron, and this in turn leads to stabilization of bipolarons with respect to dissociative decay. Moreover, the action of the magnetic field expands the range of dielectric media where bound two-polaron formation can exist. Thus for the 23Pz state, even in a dimensionless field as low as 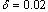 , the limitation (
, the limitation (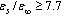 ) on the dielectric parameters of medium is reduced and will be
) on the dielectric parameters of medium is reduced and will be 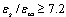 , whereas for the 23Px±iy state the effect of the magnetic field is still greater:
, whereas for the 23Px±iy state the effect of the magnetic field is still greater: 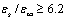 . Using the virial relation Eq. (25) is easy to show that the triplet bipolaron has spherical symmetry. Really, using the relation Eq. (25) and the condition
. Using the virial relation Eq. (25) is easy to show that the triplet bipolaron has spherical symmetry. Really, using the relation Eq. (25) and the condition 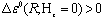 we find
we find 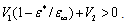 | (28) |
Here we used the follow notation for two-center integrals: 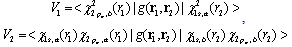 In addition we assumed that for rough estimates of the one-electron wave functions of the polaron and bipolaron are the same (this gives the underestimation of the binding energy). Hence the requirement of positive
In addition we assumed that for rough estimates of the one-electron wave functions of the polaron and bipolaron are the same (this gives the underestimation of the binding energy). Hence the requirement of positive 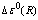 of Eq. (28) reduces to the inequality
of Eq. (28) reduces to the inequality 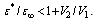 . Using numerical values for V1 and V2 we obtain
. Using numerical values for V1 and V2 we obtain 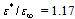 which is found in accordance with the result of the variational calculations of the triplet bipolaron. For the case R ≠ 0 near zero, when S=
which is found in accordance with the result of the variational calculations of the triplet bipolaron. For the case R ≠ 0 near zero, when S=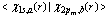 <<1, the inequality
<<1, the inequality 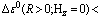
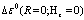 is satisfied if
is satisfied if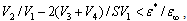 | (29) |
which is always valid, since V1 > V2 > 0, V3 ≈ SV1, V4 ≈ SV2 and S also are all positive. Here 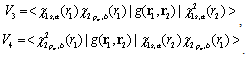 Thus, it has been shown that R = 0 is really the total energy minimum. Consequently, in contrast to the singlet axial- symmetric bipolarons[9,10] electron-excited triplet bipolarons are spherically symmetrical formations.
Thus, it has been shown that R = 0 is really the total energy minimum. Consequently, in contrast to the singlet axial- symmetric bipolarons[9,10] electron-excited triplet bipolarons are spherically symmetrical formations.
3. Interelectron Correlations
We now show that the inclusion of interelectron correlation leads to deeper potential well of the triplet bipolaron and extension of the dielectric media in which such formation may be exist. In the Hartree-Fock (HF) approximation for electrons with parallel spin correlation is partially accounted. However, this approximation not taken into account intershell Coulomb correlation. To account for this correlation, we need to introduce explicitly the interelectronic distance r12 in the symmetrized two-electron wave function 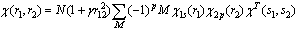 | (30) |
here 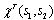 is antisymmetric spin-function, M is the operator of electron coordinates permutation, p is number of individual pairs of transpositions in the permutation M, γ is the additional variational parameter. As shown by calculations for extreme case
is antisymmetric spin-function, M is the operator of electron coordinates permutation, p is number of individual pairs of transpositions in the permutation M, γ is the additional variational parameter. As shown by calculations for extreme case  parameter
parameter  . We make up the ratio for the self-consistent total energies.
. We make up the ratio for the self-consistent total energies. 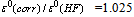 (magnetic field Hz = 0). That is, the electron-electron correlations leads to a decrease in the total energy of the triplet bipolaron in comparison with the Hartree-Fock approximation and the expansion of the existence of the triplet bipolaron. Macroscopic dielectric constants must now satisfy the weaker inequality
(magnetic field Hz = 0). That is, the electron-electron correlations leads to a decrease in the total energy of the triplet bipolaron in comparison with the Hartree-Fock approximation and the expansion of the existence of the triplet bipolaron. Macroscopic dielectric constants must now satisfy the weaker inequality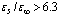 , than in the case of quasi-independent electrons
, than in the case of quasi-independent electrons 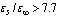 . An alternative method of accounting electronic correlations is the series enhancement of electronic part of the wave function of the electronic configurations of the same symmetry (multiplicity). Assuming that the total spin S is a constant of the motion, we expand the electronic wave function of the 23Pz,x±iy term of the system of eigenfunctions of a centrally symmetric field
. An alternative method of accounting electronic correlations is the series enhancement of electronic part of the wave function of the electronic configurations of the same symmetry (multiplicity). Assuming that the total spin S is a constant of the motion, we expand the electronic wave function of the 23Pz,x±iy term of the system of eigenfunctions of a centrally symmetric field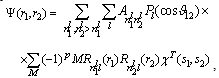 | (31) |
where 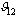 is the angle between the radius vectors of the first and second electrons. For example, take into account the superposition Eq. (31), two excited elecronic configurations 1s2p and 2s2p. Moreover, the radial part of the single-particle 2s function chosen in the quasi-Coulomb form
is the angle between the radius vectors of the first and second electrons. For example, take into account the superposition Eq. (31), two excited elecronic configurations 1s2p and 2s2p. Moreover, the radial part of the single-particle 2s function chosen in the quasi-Coulomb form 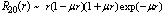 . Extremalization two-particle functional (2) under the additional condition of orthonormality of electronic configurations leads to the next value of self-consistent total energy (for the extreme case
. Extremalization two-particle functional (2) under the additional condition of orthonormality of electronic configurations leads to the next value of self-consistent total energy (for the extreme case  ,
,  >10):
>10): 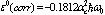 when the values of parameters are optimal ,
when the values of parameters are optimal , 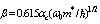 ,
, 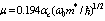 , and mixing ratio
, and mixing ratio 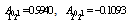 . Dimensionless ratio
. Dimensionless ratio 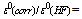 1.02. That is already in the approximation of two configurations of most of the correlation energy can be accounted for.
1.02. That is already in the approximation of two configurations of most of the correlation energy can be accounted for.
4. Conclusions
We establish conditions for the existence of electronically excited triplet bipolarons. It is shown that under certain conditions imposed on the macroscopic parameters of the dielectric medium, there may be quasi-stationary two- electron bipolaron formation in the triplet spin state. In contrast to the singlet bipolarons, triplet bipolarons are spherically symmetric. Similarly, the triplet bipolaron in 23P state can exist triplet 23S bipolaron. In this case, one electron occupies the 1s single-electron level and the other electron occupies the 2s one-electron level[10]. However, the triplet term in the energy scale is lower than the initial single-particle states. The prohibition on the electron spin makes it impossible for the radiative deactivation of electron-excited triplet formation. Nonradiative deactivation is not effective also[10]. The action of a uniform magnetic field stabilizes the triplet bipolaron.According to estimates[10], the nonradiative decay of the triplet bipolaron is of order (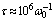 ), which is considerably longer than the characteristic phonon time (
), which is considerably longer than the characteristic phonon time (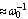 ), as well as time (
), as well as time (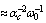 ) electron oscillations in the bipolaron potential well. The damping of the triplet bipolaron (
) electron oscillations in the bipolaron potential well. The damping of the triplet bipolaron (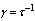 ) due to phonon emission decreases rapidly with increasing
) due to phonon emission decreases rapidly with increasing  . Thus, the triplet bipolaron for times of order
. Thus, the triplet bipolaron for times of order  can be regarded as an equilibrium. In principle such triplet electron-excited bipolarons being the quasi-stationary formations, but with a sufficiently long lifetime, can transfer the trapped energy in a uniform electric field in the selected direction.
can be regarded as an equilibrium. In principle such triplet electron-excited bipolarons being the quasi-stationary formations, but with a sufficiently long lifetime, can transfer the trapped energy in a uniform electric field in the selected direction.
References
| [1] | V. K. Mukhomorov, “Singlet and triplet states of a continual bipolaron for adiabatic and strong coupling,” Sov. Phys. – Optics and Spectroscopy, vol. 74, pp. 644-655, June 1993. |
| [2] | S. I. Pekar. Research in Electron Theory of Crystals. US AEC Report AEC-tr-5575, Ed. USA, 1963. |
| [3] | V. K. Mukhomorov, “Singlet and triplet states of quasimolecular dimer solvated in ammonia,” Sov. Phys. - Optics and Spectroscopy., vol. 69, pp.43-46, July 1990. |
| [4] | G. Iadonisi, M. Chiofolo, V. Cataudella, D. Ninno, “Phonon-plasmon cooperative effects in the dilute large-bipolaron gas: A possible mechanism for hogh-Tc superconductivity,” Phys. Rev. B, vol. 48, pp. 12966-12978, Nov. 1993-I. |
| [5] | S. Sahoo, “A variational calculation of the stability of the two centre Fröhlich bipolaron,” Phys. Lett. A, vol. 195, pp. 105-109, Sept. 1994. |
| [6] | W. B. da Costa, P. M. Peeters, “Phase diagram for large two-dimensional bipolarons in a magnetic field,” Phys. Rev. B, vol.57, pp.10569-10575, May 1998-I. |
| [7] | R. T. Senger, A. Ercelebi, “On the stability of Fröhlich bipolarons in spherical quantum dots,” Eur. Phys. J. B, vol.26, pp.5549-5560, May 2002. |
| [8] | V. K. Mukhomorov, “Stability of bipolarons, electron-electron correlations, the variational principle, and the virial theorem,” Physics of the Solid State, v.48, pp.864-870, May 2006. |
| [9] | R. T. Senger, B. Kozal, A. Chatterjee, A. Ercelebi, “Hartree-Fock approximation of bipolaron state in quantum dotes and wires,” Eur. Phys. J. B, vol.78, pp.525-529, Dec. 2010. |
| [10] | V. K. Mukhomorov, Bipolarons. (Structure. Properties). Ed. Saarbrücken, Germany: Lambert Academic Publishing, 2011. |
| [11] | E. Kartheuser, R. Evrard, J. Devreese, “Mechanism of absorption of light by free continuum polarons,” Phys. Rev. Lett., vol.22, pp.94-97, Jan. 1969. |
| [12] | R.McWeeny, B.T.Sutcliffe, Methods of Molecular Quantum Mechanics. Ed. New York, USA: Academic Press, 1969. |
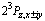 state is made. It is shown that the action of the magnetic field, on the one hand, leads to displacement of the triplet terms to the low-energy region and thus to stabilization of the bipolaron and, on the other hand, appreciable weakens the criteria that limit the conditions of their existence. It is shown that the inclusion of electron-electron correlation leads to the stabilization of the triplet bipolaron, as well as to expand the boundaries of his existence.
state is made. It is shown that the action of the magnetic field, on the one hand, leads to displacement of the triplet terms to the low-energy region and thus to stabilization of the bipolaron and, on the other hand, appreciable weakens the criteria that limit the conditions of their existence. It is shown that the inclusion of electron-electron correlation leads to the stabilization of the triplet bipolaron, as well as to expand the boundaries of his existence.
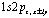 state. Such two polarons species can be formed in polar media where autolocalization is associated with the formation of a fairly deep and wide polarization potential well. It was shown that polarons can exist in the ground and relaxation-excited states. As is well known[2], optical excitation of a polaron Franck-Condon transition occurs between the electronic 1s and
state. Such two polarons species can be formed in polar media where autolocalization is associated with the formation of a fairly deep and wide polarization potential well. It was shown that polarons can exist in the ground and relaxation-excited states. As is well known[2], optical excitation of a polaron Franck-Condon transition occurs between the electronic 1s and 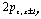 - states, the oscillator strength is ~ 0.9. At the same time the possible existence of singlet axially- symmetrical bipolarons has been widely discussed[3-10]. The most probable dipole-actives the optical transition for ground state of Landau-Pekar bipolaron will be
- states, the oscillator strength is ~ 0.9. At the same time the possible existence of singlet axially- symmetrical bipolarons has been widely discussed[3-10]. The most probable dipole-actives the optical transition for ground state of Landau-Pekar bipolaron will be 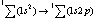 . For the special case
. For the special case 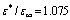 (a polaron in ammonia), we obtain the transition frequency
(a polaron in ammonia), we obtain the transition frequency 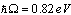 , which is very close to the experimental value 0.81eV[10].The bipolarons in triplet state will have an anomalous chemical activity and, in view of the translational invariance of the system, can transfer the trapped energy quantum in a selected direction. The spin prohibition of the emission of a photon from a metastable state is lifted as a result of relativistic interactions, but this deactivation mechanism is inefficient. Also possible are T→S (triplet→singlet) transition due to the interaction of the electron spin with the transverse phonons of the polar media. They lead to a change in the spatial symmetry of the bipolaron. From a centrally symetric state it changes to a singlet quasi-molecular bipolaron. However, in view of the small magnitude of the magnetic interactions, the spontaneous T→S transitions are of low probability. Triplet bipolarons may be treated as active centers having an inverted population relative to the ground singlet state.It is known[11] that a magnetic field lowers the energy of a polarons and stabilizes the relaxation-excited states relative to the processes of nonradiative deactivation. The present paper analyzes the conditions of triplet bipolarons existence and the effect of a magnetic field on the energy terms bipolaron in triplet state.
, which is very close to the experimental value 0.81eV[10].The bipolarons in triplet state will have an anomalous chemical activity and, in view of the translational invariance of the system, can transfer the trapped energy quantum in a selected direction. The spin prohibition of the emission of a photon from a metastable state is lifted as a result of relativistic interactions, but this deactivation mechanism is inefficient. Also possible are T→S (triplet→singlet) transition due to the interaction of the electron spin with the transverse phonons of the polar media. They lead to a change in the spatial symmetry of the bipolaron. From a centrally symetric state it changes to a singlet quasi-molecular bipolaron. However, in view of the small magnitude of the magnetic interactions, the spontaneous T→S transitions are of low probability. Triplet bipolarons may be treated as active centers having an inverted population relative to the ground singlet state.It is known[11] that a magnetic field lowers the energy of a polarons and stabilizes the relaxation-excited states relative to the processes of nonradiative deactivation. The present paper analyzes the conditions of triplet bipolarons existence and the effect of a magnetic field on the energy terms bipolaron in triplet state. 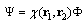
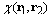 and a wave function
and a wave function 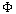 of normal vibrations of a dielectric continuum. To determine the energy of the two polarons system it is necessary to minimize the functional
of normal vibrations of a dielectric continuum. To determine the energy of the two polarons system it is necessary to minimize the functional 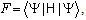
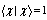 and
and 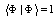 ; to describe the behavior of electrons in a polarizing medium we use the generalized Hamiltonian
; to describe the behavior of electrons in a polarizing medium we use the generalized Hamiltonian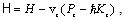
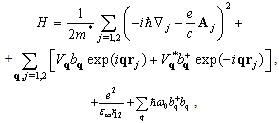
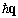 and longitudinal eigenfrequency ω0 (q = 0); and the Fourier coefficients
and longitudinal eigenfrequency ω0 (q = 0); and the Fourier coefficients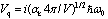
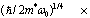
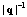 characterize the interaction of the electron with the polarization continuum. The dimensionless coupling constant is
characterize the interaction of the electron with the polarization continuum. The dimensionless coupling constant is 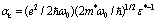 , m* is the effective electron mass in the approximation of the isotropic and quadratic law of dispersion, and V is the volume of the main region of the continuum. The effective permittivity is
, m* is the effective electron mass in the approximation of the isotropic and quadratic law of dispersion, and V is the volume of the main region of the continuum. The effective permittivity is 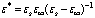 ,
, 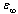 and
and 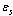 are the high-frequency and static permittivities of the polar medium. The vector potential of a constant homogeneous magnetic field directed along the z axis will be chosen in the symmetric form
are the high-frequency and static permittivities of the polar medium. The vector potential of a constant homogeneous magnetic field directed along the z axis will be chosen in the symmetric form 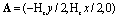 .Varying Eq. (2) with respect to and allowing for Eqs. (1) and (3), we obtain the following equation for the eigenvalues for the polarization continuum:
.Varying Eq. (2) with respect to and allowing for Eqs. (1) and (3), we obtain the following equation for the eigenvalues for the polarization continuum: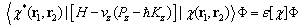
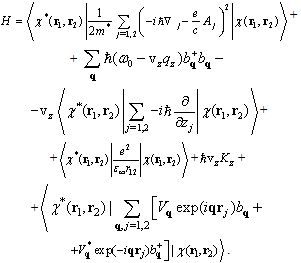
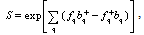
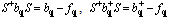 we obtain
we obtain 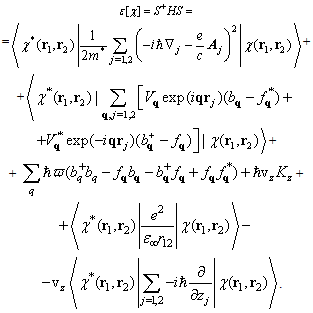
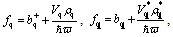
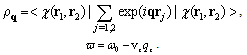 Substituting Eq.(9) into Eq.(8) we obtain the total energy functional, which takes into account the translational displacement of the bipolaron as a whole
Substituting Eq.(9) into Eq.(8) we obtain the total energy functional, which takes into account the translational displacement of the bipolaron as a whole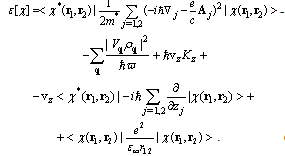
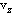 the electronic part of the wave function will be written in the form
the electronic part of the wave function will be written in the form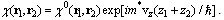
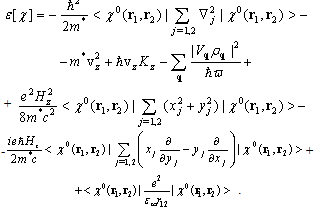
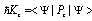 , as well as the definitions Eqs.(1) and (11), for the eigenvalue of the momentum operator, we find
, as well as the definitions Eqs.(1) and (11), for the eigenvalue of the momentum operator, we find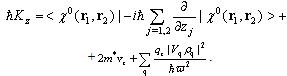
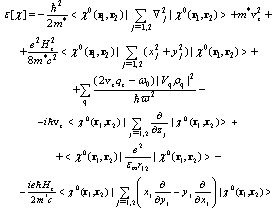
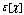 in power of
in power of 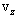 and keeping only the quadratic terms in the series, obtain
and keeping only the quadratic terms in the series, obtain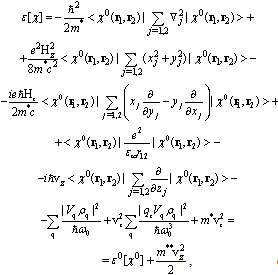
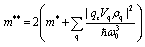
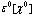 separately in Eq. (15). It is convenient henceforth to change from the q representation in Eq. (15) to a coordinate representation, and to introduce the one-electron spinless density function, which in the general case of an N-electron system may be written
separately in Eq. (15). It is convenient henceforth to change from the q representation in Eq. (15) to a coordinate representation, and to introduce the one-electron spinless density function, which in the general case of an N-electron system may be written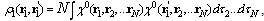
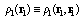 , and the two-electron spinless density function is
, and the two-electron spinless density function is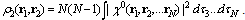
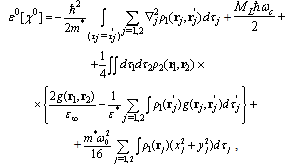
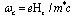 , the electron-electron interaction operator is
, the electron-electron interaction operator is 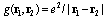 , and the energy is reckoned from the bottom of the conduction band at Hz = 0. In the derivation of Eq. (19), the identity
, and the energy is reckoned from the bottom of the conduction band at Hz = 0. In the derivation of Eq. (19), the identity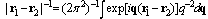 was considered, and the operator transformations of Ref. [12] were used.We shall consider triplet singly excited electronic states (for distances R → ∞ the energy of the two polaron system corresponds to the
was considered, and the operator transformations of Ref. [12] were used.We shall consider triplet singly excited electronic states (for distances R → ∞ the energy of the two polaron system corresponds to the 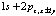 configuration).
configuration). 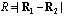 is the distance between centers of polarons gravity [1,9], while the vector ri is associated with oscillation motion of electron in polarization potential well near Ri. The two-electron wave function of the electronic excited state, approximating the eigenfunction
is the distance between centers of polarons gravity [1,9], while the vector ri is associated with oscillation motion of electron in polarization potential well near Ri. The two-electron wave function of the electronic excited state, approximating the eigenfunction 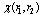 should be antisymmetric with respect to the transposition of both electrons orthogonal to the ground state. In the approximation of quasi-independent electrons, the electronic part of the two-center wave function (the centers of the potential wells are found at points a and b, separated by distance R) will be written in the Heitler-London form
should be antisymmetric with respect to the transposition of both electrons orthogonal to the ground state. In the approximation of quasi-independent electrons, the electronic part of the two-center wave function (the centers of the potential wells are found at points a and b, separated by distance R) will be written in the Heitler-London form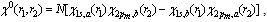
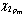 are one-particle wave functions of the 1s and 2pm states, and m = z, x±iy. The coordinate one-particle wave functions are chosen in the form of orthonormalized two-parameter Gaussian-type functions
are one-particle wave functions of the 1s and 2pm states, and m = z, x±iy. The coordinate one-particle wave functions are chosen in the form of orthonormalized two-parameter Gaussian-type functions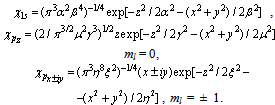
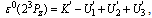
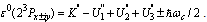
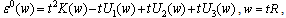
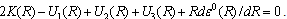
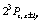 state will be stable to adiabatic dissociation by two polarons with conservation of the total spin and orbital angular momentum if the binding energy
state will be stable to adiabatic dissociation by two polarons with conservation of the total spin and orbital angular momentum if the binding energy 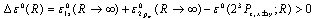 where
where 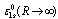 and
and 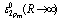 are the self-consistent total energy of the polarons in 1s and 2pm states. Figure 1 shows the total energy of the bipolaron on the distance R for dielectric parameters
are the self-consistent total energy of the polarons in 1s and 2pm states. Figure 1 shows the total energy of the bipolaron on the distance R for dielectric parameters 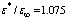 . Triplet bipolaron has minima when R = 0. For R = 0 in extreme case
. Triplet bipolaron has minima when R = 0. For R = 0 in extreme case 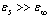 the ratio
the ratio 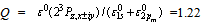 . With a decrease in the value of Q ratio decreases and reaches unity at
. With a decrease in the value of Q ratio decreases and reaches unity at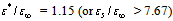 .Let us consider the change in the total energy of the triplet bipolaron in the limit of a weak magnetic field:
.Let us consider the change in the total energy of the triplet bipolaron in the limit of a weak magnetic field: 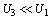 . In this case, we assume that the bipolaron has central symmetry (
. In this case, we assume that the bipolaron has central symmetry (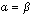 and
and 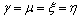 ). Hence, to determine the energy change, use may be made of the methods of perturbation theory, which for the 23Pz state gives the energy correction
). Hence, to determine the energy change, use may be made of the methods of perturbation theory, which for the 23Pz state gives the energy correction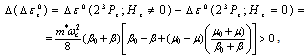
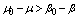 and
and 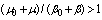 [10] it is evident that in the presence of a magnetic field
[10] it is evident that in the presence of a magnetic field 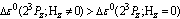 , i.e., the term of the total energy of the triplet bipolaron becomes lower, and is stabilization takes place.
, i.e., the term of the total energy of the triplet bipolaron becomes lower, and is stabilization takes place. 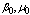 and
and 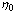 are the parameters for Hz = 0. The corresponding inequality can also be written for
are the parameters for Hz = 0. The corresponding inequality can also be written for 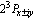 term:
term: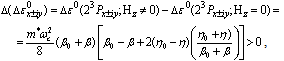
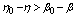 and
and 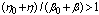 . In magnetic fields (dimensionless)
. In magnetic fields (dimensionless) 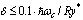 , where
, where 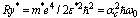 , the change in coupling energy for states with ML = 0 and ML = ± 1 is different, and independently of the ratio of the permittivities of the medium, always
, the change in coupling energy for states with ML = 0 and ML = ± 1 is different, and independently of the ratio of the permittivities of the medium, always 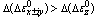 . However, in magnetic fields:
. However, in magnetic fields: 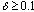 , the energy change of the 23Pz term becomes more significant than that of the 23Px±iy term, and for polar media with a smaller ratio of
, the energy change of the 23Pz term becomes more significant than that of the 23Px±iy term, and for polar media with a smaller ratio of 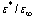 , this shift takes place in lower fields.
, this shift takes place in lower fields.
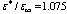

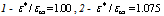
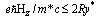 , a variation calculation of the change in total energy terms is shown in Fig.2 for two cases:
, a variation calculation of the change in total energy terms is shown in Fig.2 for two cases: 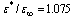 and extreme ratio
and extreme ratio 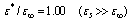 . These results fully confirm the conclusions that follow from Eqs. (26) and (27). Irrespective of the permittivity ratio, a constant homogeneous magnetic field decreases the energy of the triplet bipolaron, and this in turn leads to stabilization of bipolarons with respect to dissociative decay. Moreover, the action of the magnetic field expands the range of dielectric media where bound two-polaron formation can exist. Thus for the 23Pz state, even in a dimensionless field as low as
. These results fully confirm the conclusions that follow from Eqs. (26) and (27). Irrespective of the permittivity ratio, a constant homogeneous magnetic field decreases the energy of the triplet bipolaron, and this in turn leads to stabilization of bipolarons with respect to dissociative decay. Moreover, the action of the magnetic field expands the range of dielectric media where bound two-polaron formation can exist. Thus for the 23Pz state, even in a dimensionless field as low as 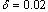 , the limitation (
, the limitation (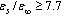 ) on the dielectric parameters of medium is reduced and will be
) on the dielectric parameters of medium is reduced and will be 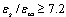 , whereas for the 23Px±iy state the effect of the magnetic field is still greater:
, whereas for the 23Px±iy state the effect of the magnetic field is still greater: 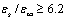 . Using the virial relation Eq. (25) is easy to show that the triplet bipolaron has spherical symmetry. Really, using the relation Eq. (25) and the condition
. Using the virial relation Eq. (25) is easy to show that the triplet bipolaron has spherical symmetry. Really, using the relation Eq. (25) and the condition 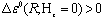 we find
we find 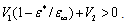
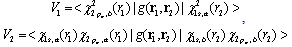 In addition we assumed that for rough estimates of the one-electron wave functions of the polaron and bipolaron are the same (this gives the underestimation of the binding energy). Hence the requirement of positive
In addition we assumed that for rough estimates of the one-electron wave functions of the polaron and bipolaron are the same (this gives the underestimation of the binding energy). Hence the requirement of positive 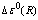 of Eq. (28) reduces to the inequality
of Eq. (28) reduces to the inequality 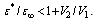 . Using numerical values for V1 and V2 we obtain
. Using numerical values for V1 and V2 we obtain 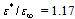 which is found in accordance with the result of the variational calculations of the triplet bipolaron. For the case R ≠ 0 near zero, when S=
which is found in accordance with the result of the variational calculations of the triplet bipolaron. For the case R ≠ 0 near zero, when S=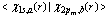 <<1, the inequality
<<1, the inequality 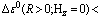
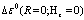 is satisfied if
is satisfied if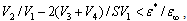
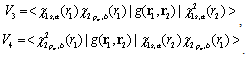 Thus, it has been shown that R = 0 is really the total energy minimum. Consequently, in contrast to the singlet axial- symmetric bipolarons[9,10] electron-excited triplet bipolarons are spherically symmetrical formations.
Thus, it has been shown that R = 0 is really the total energy minimum. Consequently, in contrast to the singlet axial- symmetric bipolarons[9,10] electron-excited triplet bipolarons are spherically symmetrical formations.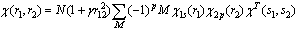
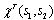 is antisymmetric spin-function, M is the operator of electron coordinates permutation, p is number of individual pairs of transpositions in the permutation M, γ is the additional variational parameter. As shown by calculations for extreme case
is antisymmetric spin-function, M is the operator of electron coordinates permutation, p is number of individual pairs of transpositions in the permutation M, γ is the additional variational parameter. As shown by calculations for extreme case  parameter
parameter 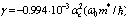 . We make up the ratio for the self-consistent total energies.
. We make up the ratio for the self-consistent total energies. 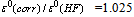 (magnetic field Hz = 0). That is, the electron-electron correlations leads to a decrease in the total energy of the triplet bipolaron in comparison with the Hartree-Fock approximation and the expansion of the existence of the triplet bipolaron. Macroscopic dielectric constants must now satisfy the weaker inequality
(magnetic field Hz = 0). That is, the electron-electron correlations leads to a decrease in the total energy of the triplet bipolaron in comparison with the Hartree-Fock approximation and the expansion of the existence of the triplet bipolaron. Macroscopic dielectric constants must now satisfy the weaker inequality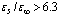 , than in the case of quasi-independent electrons
, than in the case of quasi-independent electrons 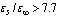 . An alternative method of accounting electronic correlations is the series enhancement of electronic part of the wave function of the electronic configurations of the same symmetry (multiplicity). Assuming that the total spin S is a constant of the motion, we expand the electronic wave function of the 23Pz,x±iy term of the system of eigenfunctions of a centrally symmetric field
. An alternative method of accounting electronic correlations is the series enhancement of electronic part of the wave function of the electronic configurations of the same symmetry (multiplicity). Assuming that the total spin S is a constant of the motion, we expand the electronic wave function of the 23Pz,x±iy term of the system of eigenfunctions of a centrally symmetric field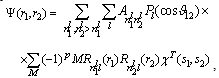
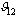 is the angle between the radius vectors of the first and second electrons. For example, take into account the superposition Eq. (31), two excited elecronic configurations 1s2p and 2s2p. Moreover, the radial part of the single-particle 2s function chosen in the quasi-Coulomb form
is the angle between the radius vectors of the first and second electrons. For example, take into account the superposition Eq. (31), two excited elecronic configurations 1s2p and 2s2p. Moreover, the radial part of the single-particle 2s function chosen in the quasi-Coulomb form 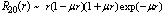 . Extremalization two-particle functional (2) under the additional condition of orthonormality of electronic configurations leads to the next value of self-consistent total energy (for the extreme case
. Extremalization two-particle functional (2) under the additional condition of orthonormality of electronic configurations leads to the next value of self-consistent total energy (for the extreme case 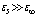 ,
, 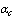 >10):
>10): 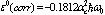 when the values of parameters are optimal ,
when the values of parameters are optimal , 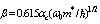 ,
, 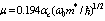 , and mixing ratio
, and mixing ratio 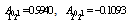 . Dimensionless ratio
. Dimensionless ratio 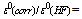 1.02. That is already in the approximation of two configurations of most of the correlation energy can be accounted for.
1.02. That is already in the approximation of two configurations of most of the correlation energy can be accounted for.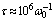 ), which is considerably longer than the characteristic phonon time (
), which is considerably longer than the characteristic phonon time (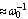 ), as well as time (
), as well as time (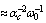 ) electron oscillations in the bipolaron potential well. The damping of the triplet bipolaron (
) electron oscillations in the bipolaron potential well. The damping of the triplet bipolaron (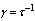 ) due to phonon emission decreases rapidly with increasing
) due to phonon emission decreases rapidly with increasing 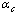 . Thus, the triplet bipolaron for times of order
. Thus, the triplet bipolaron for times of order 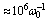 can be regarded as an equilibrium. In principle such triplet electron-excited bipolarons being the quasi-stationary formations, but with a sufficiently long lifetime, can transfer the trapped energy in a uniform electric field in the selected direction.
can be regarded as an equilibrium. In principle such triplet electron-excited bipolarons being the quasi-stationary formations, but with a sufficiently long lifetime, can transfer the trapped energy in a uniform electric field in the selected direction. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML