-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Condensed Matter Physics
p-ISSN: 2163-1115 e-ISSN: 2163-1123
2012; 2(3): 67-72
doi: 10.5923/j.ajcmp.20120203.03
Isotope Effect as a Probe of the Role of Phonons in Conventional and High Temperature Superconductors
Manzoor A. Malik , Bilal A. Malik
Department of Physics, University of Kashmir, Srinagar, 190006, J&K, India
Correspondence to: Manzoor A. Malik , Department of Physics, University of Kashmir, Srinagar, 190006, J&K, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
We review the role of phonons in the mechanism of both conventional and high temperature superconductivity. We find that while on one hand most of the conventional superconductors fall within the framework of the BCS phonon-mediated pairing, on the other hand the complexity of the structural properties of High superconductors allows determination of only the partial (oxygen) isotope effect, with values ranging from negligibly small to even higher than BCS prediction. In either case, the study of isotope shift is important in its own right. We arrive at the conclusion that while phonons are central to explaining the mechanism of conventional superconductivity, their role should be taken into account for explaining High TC superconductivity, as well.
Keywords: Superconductivity, Conventional, High Temperature, Isotope Effect, Mechanism
Article Outline
1. Introduction
- One of the most important properties of metals is that their electrical resistivity decreases with the decrease of temperature. Investigation of the electrical properties of metals at low temperatures led the Dutch Physicist Heike Kamerlingh Onnes and his assistant Gilles Holst in 1911 to discover, the phenomenon of superconductivity at 4.2 K in mercury[1, 2]. The discovery of superconductivity was one of the most important experimental finding in low temperature physics of the early 20th century. Since then, tremendous theoretical and experimental efforts have been made to develop the correct theory for explaining underlying mechanism responsible for superconductivity. In the history of superconductivity, different theories have been proposed from time to time. We can broadly categorize these theoretical efforts into two types: Macroscopic and Microscopic theories. The macroscopic theories like Meissner effect[3], London equations[4], Ginsburg-Landau theory[5], do fairly explain some properties of superconductors but were inadequate to explain the underlying mechanism of superconductivity.The first microscopic theory of superconductivity was put forth by Bardeen, Cooper and Schrieffer in 1957[6]. For conventional superconductors, this theory satisfactorily explains the properties like Penetration Depth, the Energy Gap, Coherence Length, Isotope Effect and other properties as summarized in[7,8]. As BCS theory could explain almost all the properties of conventional superconductors, supported by fairly good agreement between theory and experiment, it was considered to be ultimate theory for the mechanism of superconductivity.However, the discovery of high temperature superconductivity[9], particularly above the liquid nitrogen temperature[10–13] posed serious challenges to the validity of BCS theory. Despite being the most active area of research and its limitless scope for applications, the mechanism remains elusive, owing to the unusual nature of properties exhibited by these high TC materials, particularly cuprates. The properties like very small or no isotope shift, high transition temperature, short coherence length, low density of states, low carrier concentration, electric and magnetic anisotropies are markedly different from those for the conventional low temperature superconductors. These discrepancies which could not be accommodated within the original BCS formalism led researchers to search for alternative theories of high temperature superconductivity including modification to the original BCS framework so as to somehow account for these unusual properties of High TC superconductors.Among the various properties of superconductors, the one central to the development of BCS theory was the observation of Isotope Effect in superconductors. In conventional superconductors, it was found that transition temperature is inversely proportional to the square root of the isotopic mass (
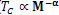 where α ≈ 0.5). Isotopes being chemically identical, a change in TC on substituting one isotope for other implies that the lattice vibrations are somehow important for superconductivity. This was the basis for the phonon mediated pairing interaction envisaged in the BCS theory via the formation of cooper pairs[14].Certain conventional superconductors have isotope effect exponent equal to the predicted value of BCS theory and lot of materials have small but appreciable deviations from the BCS value, which for practical purposes can be treated within the BCS framework. But there are conventional superconductors which have isotope effect much larger than BCS value which though may be exceptions, raise serious challenge against theory[15,16].On the other hand, the story of high temperature superconductors is interesting and challenging. The study of oxygen isotope effect has been carried out in almost all cuprates. For some family of cuprates, the oxygen isotope exponent (OIE) is very small than BCS prediction[17]. This suggests that phonons may not be playing any role in the occurrence of superconductivity in cuprates. However, for a particular family of doped cuprates, the oxygen isotope exponents (OIE) increase with decreasing TC and can be even larger than BCS value[18]. Such an anomalously large OIE imply that phonons have a definite role in the superconductivity.Any correct theory for explaining the mechanism of superconductivity, in particular, for high TC superconductors has to account for both small OIE in optimally-doped samples and anomalously large OIE in the underdoped samples.Motivated by the central role that isotope effect plays in explaining conventional superconductivity and the recent findings that phonons may be important for high TC superconductors, we intend, in this review, to put together the efforts of various groups in trying to explain both conventional and high TC superconductivity.
where α ≈ 0.5). Isotopes being chemically identical, a change in TC on substituting one isotope for other implies that the lattice vibrations are somehow important for superconductivity. This was the basis for the phonon mediated pairing interaction envisaged in the BCS theory via the formation of cooper pairs[14].Certain conventional superconductors have isotope effect exponent equal to the predicted value of BCS theory and lot of materials have small but appreciable deviations from the BCS value, which for practical purposes can be treated within the BCS framework. But there are conventional superconductors which have isotope effect much larger than BCS value which though may be exceptions, raise serious challenge against theory[15,16].On the other hand, the story of high temperature superconductors is interesting and challenging. The study of oxygen isotope effect has been carried out in almost all cuprates. For some family of cuprates, the oxygen isotope exponent (OIE) is very small than BCS prediction[17]. This suggests that phonons may not be playing any role in the occurrence of superconductivity in cuprates. However, for a particular family of doped cuprates, the oxygen isotope exponents (OIE) increase with decreasing TC and can be even larger than BCS value[18]. Such an anomalously large OIE imply that phonons have a definite role in the superconductivity.Any correct theory for explaining the mechanism of superconductivity, in particular, for high TC superconductors has to account for both small OIE in optimally-doped samples and anomalously large OIE in the underdoped samples.Motivated by the central role that isotope effect plays in explaining conventional superconductivity and the recent findings that phonons may be important for high TC superconductors, we intend, in this review, to put together the efforts of various groups in trying to explain both conventional and high TC superconductivity.2. Isotope Effect in Conventional Superconductors
- Isotope effect studies have been vital to the development of the microscopic theory of superconductivity. The first piece of evidence about the existence of isotope effect in mercury was reported in 1950 by Maxwell[19] and independently by Reynold et al.[20]. They found that the critical temperature TC of mercury varies as an inverse function of isotopic mass. The argument that isotope mass enters into the formation of the superconducting phase implies that superconductivity is not purely electronic in origin. In the same year, Frohlich[21] proposed that same electron lattice interaction responsible for the scattering of conduction electrons by lattice vibrations provides a necessary glue between electrons. Frohlich’s theory got a strong base from the experimental observation of isotope effect and played a key role in understanding microscopic mechanism of superconductivity. In 1956, Cooper[14] demonstrated that a pair of electrons can interact above a Fermi surface with an interaction of a kind that might be expected due to phonon and screened coulomb fields. If there is a net attraction between the electrons, it turns out that they can form bound states, though their energy is larger than zero. The properties of non-interacting system of bound pairs are very suggestive of those which could produce superconducting state. However, the existence of electron pairs does not necessarily imply a phonon mediated pairing. Indeed Bose condensation, as considered by Schafroth[22] is also a possible mechanism for superconductivity, but unfortunately the model was not able to explain one of the important experimentally observed property of isotope effect discovered earlier by Maxwell and Reynold. Finally in 1957 Bardeen, Cooper and Schrieffer[6], in view of experimental observation of isotope effect in mercury discovered by Maxwell[19] and Reynold[20] followed by theoretical consideration of Frolich[21] and inadequacy of Schafroths condensation[22], put forward first successful microscopic theory, which explains most of the physical properties observed in conventional superconductors. Within the framework of BCS microscopic theory, one has relation between transition temperature TC, typical phonon frequency ω (e.g Debye frequency) and interaction strength
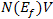 as
as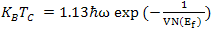 | (1) |
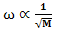 | (2) |
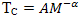 | (3) |
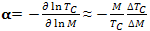 | (4) |
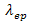 is related to spectral function α2(ω)F (ω), as defined by the product of phonon density of states F(ω) and the frequency dependent average electron phonon interaction α2 (ω). Eliashberg’s equations were solved by McMillan[52] by taking into account the coulomb repulsion between electrons, which was one of the obvious reason for the discrepancy between theory and experimental observations and the retarded nature of phonon induced interaction:
is related to spectral function α2(ω)F (ω), as defined by the product of phonon density of states F(ω) and the frequency dependent average electron phonon interaction α2 (ω). Eliashberg’s equations were solved by McMillan[52] by taking into account the coulomb repulsion between electrons, which was one of the obvious reason for the discrepancy between theory and experimental observations and the retarded nature of phonon induced interaction: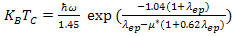 | (5) |
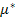 is the effective coulomb repulsion. Under
is the effective coulomb repulsion. Under 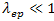 i.e weak interaction, it reduces to equation (1) where
i.e weak interaction, it reduces to equation (1) where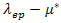 substitutes the role of N(Ef)V. As a result, in strong-coupling superconductors, the isotope effect exponent has no longer a universal value and is given by
substitutes the role of N(Ef)V. As a result, in strong-coupling superconductors, the isotope effect exponent has no longer a universal value and is given by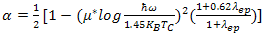 | (6) |
3. Isotope Effect in High TC Cuprates Superconductors
- The discovery of superconductivity in La2−x Bax CuO4 by Bednorz and Muller in 1986[9] prompted a burst of experimental and theoretical investigations in these systems in order to clarify the microscopic pairing mechanism for high temperature superconductivity. However, the mechanism is still highly controversial because the opinions as regards the role of electron phonon interaction vary widely[53–55]. Also, the unprecedentedly high transition temperatures in some cuprates were difficult to reconcile with the conventional phonon mediated mechanism which could account for a maximum TC of 30K[52]. Existence of short coherence length raises further challenges against BCS theory.Cuprates have a complex structure as compared to elemental superconductors and essentially have layered character, confirmed by the anisotropy of their properties. Usually cuprates consist of four layers: (a) Conducting DO2 layer (i.e CuO2 planes), (b) C separating Layer typically like Ca or Y, (c) BO bridging layer typically like BaO, LaO or SrO, and (d) AO additional layer like BiO, HgO or TlO. Superconductivity is believed to take place in CuO2 planes which are present in all high TC superconductors, but the number of CuO2 planes varies among the different families of cuprates, ranging from a single-layer up to an infinite-layer structure. Thus, the existence of layer structure introduces complexity in the investigation of isotope effect in cuprates.Hence, if a superconductor is composed of different elements like cuprates, one defines a partial isotope coefficient as
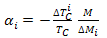 | (7) |
|
4. Conclusions
- The studies of isotope substitution can be utilized as a very effective candidate in revealing the underlying pairing mechanism of superconductivity. We have discussed isotope substitution effect in both conventional and unconventional superconductors. Measurements of the isotope effect on the transition temperature TC provides a key experimental evidence for phonon-mediated pairing, supported strongly by the BCS theory of superconductivity in most conventional superconductors. There are some conventional superconductors which have a very small isotope effect, but can be treated within the framework of Eliashberg theory and thus still be consistent with phonon mediated pairing mechanism. Therefore, we can conclude that superconductivity in conventional is not of purely electronic origin but phonons have an obvious role in the occurrence of superconductivity. However, the situation in high TC cuprates is very interesting. In optimally doped cuprates, the OIE is very small suggesting that phonons might not have any role in the occurrence of high TC superconductivity. However, for a particular family of doped cuprates the OIE increases with decreasing TC, and can even be larger than BCS prediction. Thus the existence of strong OIE implies phonons play an important role in high temperature superconductivity, as well. Any correct theory for describing the physics of high TC superconductors must be consistent with small OIE in optimally doped samples and large OIE in underdoped samples. Although, the interest in phonons (as mediators) in explaining high TC superconductivity has waxed and waned, the current findings suggest that any theory of high TC cannot ignore the role of phonons.High temperature superconductivity, however, raises serious challenges to the phonon only mechanism particularly, because of observation of short coherence length, small or no isotope shift and high TC. Many scientists opined that BCS theory may not work for high TC superconductors, though the situation has changed a bit now. In fact for organic and heavy fermion superconductors BCS model had already been ruled out. As an alternative to phonon almost all elementary excitation of solids were proposed as mediators of electron pairs. However, none of them could satisfactorily explain the basic feature of high TC superconductors. There are many reasons to believe that electron-phonon interaction may still be behind high TC superconductivity or spin fluctuations may hold the key. In a recent paper[64], it is demonstrated that bosonic excitations of the electronic origin may be the most favoured candidates for the formation of the high TC superconducting state. The fact that high TC superconductors exhibit strange and complex properties difficult to completely reconcile with one model or the other, it would be unwise to completely commit oneself to any one theory or model. It is important to look for models which interpret known results and also make predictions that can be verified. Despite the enormous progress made, high temperature superconductivity continues to challenge our intellect.
ACKNOWLEDGEMENTS
- The authors would like to thank the anonymous reviewer for inviting our attention to some recent works that helped improve the objectivity of the manuscript.
References
| [1] | H. K. Onnes, Comm. Physical Lab. Univ. Leiden No.120b and 122b, (1911) |
| [2] | R. Simon and A. Smith, Superconductors: Conquering Technology’s New Frontier (Plenum, New York) 1988 |
| [3] | W. Meissner and R. Ochsenfeld , Naturwissen 21, 787 (1933) |
| [4] | F. London and H. London, Proc. Roy. Soc. A149 71 Physica 2, 341 (1935) |
| [5] | V. L. Ginsburg and L. D. Landau, Zh. Eksperim. i Teor. Fiz. 20, 1064 (1950) |
| [6] | J. Bardeen, L. N. Cooper and J.R. Schrieffer, Phys. Rev. 108, 1175 (1957) |
| [7] | C. P. Poole Jr., (ed.) Hand book of Superconductivity (New York Acedemic Press) 2000 |
| [8] | C. P. Poole Jr. et al, Superconductivity (New York Academic Press) 1995 |
| [9] | J. G. Bednorz and K. A. Muller, Z. Phys. B 64, 189 (1986) |
| [10] | M. K. Wu et al, Phys. Rev. Lett. 58, 908 (1987) |
| [11] | Z. Z. Sheng, Applied Physics Letters 52, 988 (1993) |
| [12] | C. N. R. Rao et al, Nature 326, 856 (1987) |
| [13] | L. Gao et al, Phys. Rev. B 50, 4260 (1994) |
| [14] | L. N. Cooper, Phys. Rev. 104, 1189 (1956) |
| [15] | X. Q. Haung arxiv:1102.1467v1 (2011) |
| [16] | P. Auban-Senzier et al, Synthetic Metals 55-57, 3027 (1993) |
| [17] | J. P. Franck, Physical properties of High Temperature Superconductors IV ed D M Ginsberg (Singapore: World Scientific) 1994 |
| [18] | M. K. Crawford et al., Phys. Rev. B 41, 282 (1990) |
| [19] | E. Maxwell, Phys. Rev. 78, 477 (1950) |
| [20] | C. A. Reynolds, B. Serin , W. H. Wright and L. B. Nesbitt, Phys. Rev. 78, 467 (1950) |
| [21] | H. Frolich, Phys. Rev.79, 845 (1950) |
| [22] | M.R. Schafroth, Phys. Rev. 100, 463 (1955) |
| [23] | L. R. Testardi, J. H. Wernick and W. A .Royer , Solid St. commun. 15, 1 (1974 ) |
| [24] | J. R. Gravaler, M. A. Janocoko and C. R. Jones, J. Applied Phys. 45, 3009 (1974) |
| [25] | S. Fujita and S. Goday, Theory of high Temperature Superconductivity ( Academic Publishers, Kulwer) 2003 |
| [26] | P. J. Ford and G. A. Saunder, The Rise of Superconductors ( New York CRC Press) 2005 |
| [27] | A. Marouckine, Room Temperature Superconductivity (Cambridge UK Cambridge Science publishing) 2004 |
| [28] | C. A. Reynolds, B. Serin and L. B.Nesbitt, Phys. Rev. 84, 691 (1951) |
| [29] | E. A. Lynton, Superconductivity Methuen London (1969) |
| [30] | J. L. Olsen, Cryogenics 2, 356 (1963) |
| [31] | E. Maxwell , Rev. Mod. Phys. 36, 144 (1964) |
| [32] | B. T. Mathias, T. H. Geballe, E. Corenzwit and G. W. Hull Jr., Phys. Rev. 129, 1025 (1963) |
| [33] | E. Bucher and C.Palmy, Phys. Letters 24 A, 340 (1967) |
| [34] | R. E. Fassnacht and J. R. Dillinge, Phys. Rev. Letters 17, 255 (1966) |
| [35] | D. C. Larbalestier, A. Gurevich, D. M. Feldmann and A. Polyanski , Nature insight 414, 368 (2001) |
| [36] | D. G. Hinks, H. Clauss and J. D. Jorgensen, Nature 411, 457 (2001) |
| [37] | R. A. Hein and J. W. Gibson, Phys. Rev. 131, 1105 (1963) |
| [38] | E. Bucher, J. Muller, J. L. Olsen and C. Palmy, Phys. letters 15, 303 (1965) |
| [39] | T. H. Geballe, B. T. Mathias, G. W. Hull Jr. and E. Corenzwit, Phys. Rev. Letters 6, 275 (1961) |
| [40] | D. K. Finnemore and D. E. Mapother, Phys. Rev. Letters 9, 288 (1962) |
| [41] | J. W. Gibson and R. A. Hein, Phys. Rev. 141, 407 (1966) |
| [42] | T. H. Geballe and B. T. Mathias, IBM J. Res. Develop 6, 256 (1962) |
| [43] | R. D. Fowler, J. D. G. Linsday, R. W. White, H. H. Hill and B.T.Mathias, Phys. Rev. letters19, 892 (1967) |
| [44] | N. W. Aschroft and M.Croyt, Europhys. Lett. 23, 605 (1993) |
| [45] | Yu. N. Gartesian et al., Phys. Rev. B 49, 13299 (1994) |
| [46] | A. P. Ramirez et al, Phys. Rev. Lett. 68, 1058 (1992) |
| [47] | T. W. Ebbsen et al, Nature 355, 620 (1992) |
| [48] | B. Stritzker and W. Buckel, Z. Phys. 25, 71 ( 1972) |
| [49] | R. J. Muller and C. B.Scatterthwaite , Phys. Rev. Lett. 34, 144 (1975) |
| [50] | J. A. Schlueter et al, Physica C 265, 163 (1996) |
| [51] | G. M. Eliashberg, Sov-Phys.-JETP 11, 696 (1960) |
| [52] | W. L. McMillan, Phys. Rev. 167, 331 (1968) |
| [53] | V. J. Emery, Phys. Rev. Lett. 58, 2794 (1987) |
| [54] | P. W. Anderson, Science 235, 1196 (1987) |
| [55] | A. S. Alexandrov and N. F. Mott, Int. J. Mod. Phys. B 8, 2075 (1994) |
| [56] | G. M. Zhao, Physica Scripta 83, 038302 (2011) |
| [57] | K. Yoshida et al, Physica C 156, 481 (1988) |
| [58] | M. K. Crawford et al., Science 250, 1390 (1990) |
| [59] | P. W. Anderson, The theory of Superconductivity in High-Tc cuprate superconductors (Princeton, NJ: Princeton university Press) 1998 |
| [60] | H. J. Boremann, D. E. Morris, H. B.Liu and P. K. Narwankar, Physica C 191, 211 (1992) |
| [61] | J. P. Franck, S.Harker and J. H. Brewer, Phys. Rev. Lett. 71, 283 (1993) |
| [62] | G. M. Zhao, K. K. Singh, A. P. B. Sinha and D. E. Morris, Phys. Rev.B 52, 6840 (1995) |
| [63] | G. M. Zhao, K. Conder, H. Keller and K. A. Muller, J. Phys.: Condens. Matter 10, 9055 (1998) |
| [64] | S. Dal Conte et al Science 335, 1600 (2012) |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML