-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Condensed Matter Physics
p-ISSN: 2163-1115 e-ISSN: 2163-1123
2012; 2(3): 57-62
doi:10.5923/j.ajcmp.20120203.01
Spin-Orbital Effect of Diexciton in Quantum Dots
1Sci. & Tech. Park, University of Tehran, Tehran, Islamic Republic of Iran
2Faculty of physics, department of theoretical physics, FKN University, Almaty, 92 Tolebi St. Kazakhstan
Correspondence to: Arezu Jahanshir, Sci. & Tech. Park, University of Tehran, Tehran, Islamic Republic of Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Great efforts have been made to understand how bound state arise in the formalism of quantum field theory and to work out effective methods to calculate all characteristics of these bound states, especially their masses and binding energy. The analysis of a bound state is simplest when constituent particles can be considered to be nonrelativistic, i.e. when they travel at speeds considerably less than 'c'. We studied an exotic system (state) on the basis of investigation of asymptotic behavior of the loop function for the scalar particles in the external gauge field and determined it for the scalar particles in the with relativistic feature of interaction and have been able to obtain the mass spectrum of bound state, the constituent mass of diexciton and spin interactions and find out that determining the mass of the bound state systems requires; first of all, determining the Eigenvalue of the Hamiltonian with Coulomb potential and then calculating the mass and binding energy or spin interactions of diexciton system which we could achieve. The current paper has calculated energy spectrum and constituents mass of particles in limited core mass conditions and we could conclude that constituent mass of particle in the system is different from mass in free states. So having below conditions form inhomogeneous multi-layer environment in nanostructure  in mind, and using oscillator representation method, spin Hamiltonian coefficient of diexciton system with effective confinement potential, Coulomb effect between particles, and spin effect, will be discussed. Relation between distances properties of diexciton system and distance between two electrons in quantum dots and dependency relation will be determined in conclusion.
in mind, and using oscillator representation method, spin Hamiltonian coefficient of diexciton system with effective confinement potential, Coulomb effect between particles, and spin effect, will be discussed. Relation between distances properties of diexciton system and distance between two electrons in quantum dots and dependency relation will be determined in conclusion.
Keywords: Exciton System, Oscillator Representation Method, Spin-Orbital and Spin-Spin Interactions, Effective Mass, Constituent Mass
Cite this paper: Arezu Jahanshir, Spin-Orbital Effect of Diexciton in Quantum Dots, American Journal of Condensed Matter Physics, Vol. 2 No. 3, 2012, pp. 57-62. doi: 10.5923/j.ajcmp.20120203.01.
Article Outline
1. Introduction
- Electrons and holes in microscopic semiconductor structures can display astounding quantum behavior. These structures, namely exciton are expected to be the basis of new generation of electronic and optoelectronic and nano-structures[1,2]. Therefore description of the bound states of electron and hole is one of the general problems in quantum mechanics and nano quantum dots. This problem is studied by many authors and it is well known but in this article we try to present new approaches which help us to describe and determine better and more useful. One of the corrections in particle physics can be classified as relativistic.At present the technical achievements make it possible to create the exotic state with electron and exciton so in this quantum- relativistic state, the calculation of relativistic corrections becomes necessary. However, the conventional prescription of the calculation of the relativistic nature interaction within the framework of the phenomenological potential model of is absent at the moment and the theoretical models intended for describing the relativistic corrections to the spectrum are limited to the lowest order on the coupling constant. The other powerful stimulus for further development of the bound state theory is provided by the spectacular experimental progress in precise measurements of atomic energy levels. Calculation and analysis of energy spectrum in Coulomb potential of electron and exciton in relativistic conditions due to requirement of using higher grades of relativistic corrections have attracted physics theoreticians.We will consider this problem, according to the asymptotic behavior of the loop function in the scalar electrodynamics field and method oscillator representation in quantum physics[3]. The method presented in this paper considers relativistic effect that it concepts energy spectrum, mass and constituent mass in the exotic system and analytical is calculated with Coulomb interaction. This work is devoted to study the bound states problems, which will be carried out on the research basis asymptotical behavior of two scalar particles in external gauge field. In this case, loop function of two scalar particles with different masses
 and
and  , with average on external statistical field is considered and the Green function is used. The polarization operator in an external electromagnetic field looks like[4]:
, with average on external statistical field is considered and the Green function is used. The polarization operator in an external electromagnetic field looks like[4]: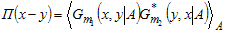 | (1) |
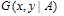 for scalar particles in an external field is determined from the equation:
for scalar particles in an external field is determined from the equation: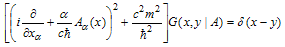 | (2) |
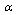 is the coupling constant of interaction. The gauge field averaging defines as follows:
is the coupling constant of interaction. The gauge field averaging defines as follows: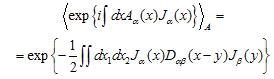 | (3) |
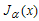 is a real current, and
is a real current, and 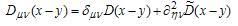 | (4) |
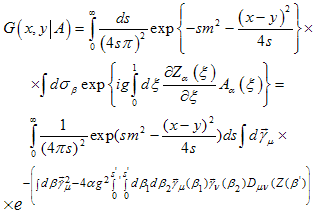 | (5) |
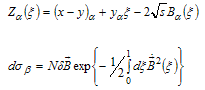 | (6) |
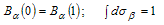 The mass of the bound state in the extreme limit is determined by the equation[4,5]:
The mass of the bound state in the extreme limit is determined by the equation[4,5]: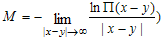 | (7) |
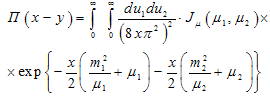 | (8) |
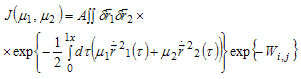 | (9) |
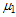 and
and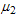 . The interaction of these particles is described by the nonlocal functional
. The interaction of these particles is described by the nonlocal functional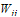 , in which are contained both potential and non-potential interaction (see appendix 1). Taking into account (8) and (9) in the extreme limit from (7) for the mass of the bound state we get (for detail see[5-7]):
, in which are contained both potential and non-potential interaction (see appendix 1). Taking into account (8) and (9) in the extreme limit from (7) for the mass of the bound state we get (for detail see[5-7]): 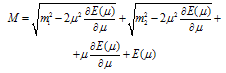 | (10) |
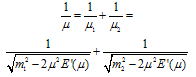 | (11) |
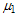 and
and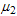 are mass components of the bound state (constituent mass of particles), which are different from the masses
are mass components of the bound state (constituent mass of particles), which are different from the masses 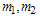 of free condition and also can be found with the help of conditions:
of free condition and also can be found with the help of conditions: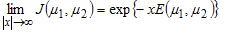 | (12) |
2. Exciton's Hamiltonian in Relativistic Corrections
- As we know one of the basic problems of nonrelativistic quantum mechanics is to determine the energy spectrum and eigenvalue of the nonrelativistic Hamiltonian of system described by the Schrödinger equation with a special potential. Complete solution of this equation has been found in 1965 (for a detailed historical literature see[8] and Landau 1977[9], for the Coulomb potential. The oscillator representation method implies that a wave function, being a bound ground state of quantum system with a good looking potential, is expanded over the oscillator basis in which coordinate and momentum are expressed through the creation and annihilation operators.The oscillator representation method in the nonrelativistic Schrödinger equation is proposed to calculate the energy spectrum for central symmetric potential allowing the existence of bound state. (for details see[10]). It is well known that for determining the mass of the bound state systems first of all one should determine the eigenvalue of the Hamiltonian with Coulomb potential. For this aim we consider the following Schrödinger equation[11,12]:
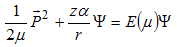 | (13) |
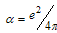 - is the coupling constant of electromagnetic interaction. z – electron and hole charge number.This equation for the wave function of orbital excitation
- is the coupling constant of electromagnetic interaction. z – electron and hole charge number.This equation for the wave function of orbital excitation 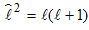 is:
is: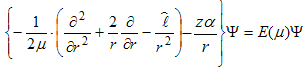 | (14) |
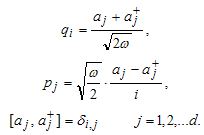 | (15) |
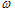 is the oscillator frequency which has been known as Hamiltonian of free oscillator and can write as follow (for more detail see[11]):
is the oscillator frequency which has been known as Hamiltonian of free oscillator and can write as follow (for more detail see[11]):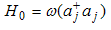 | (16) |
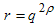 , and found the following conditions[14,15]:
, and found the following conditions[14,15]: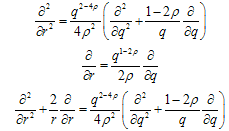 | (17) |
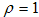 ):
):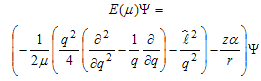 | (18) |
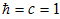 ):
):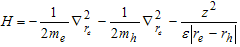 | (19) |
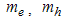 - effective mass of electron and hole. Making the co-ordinate transformation1 the Hamiltonian may be written[17]:
- effective mass of electron and hole. Making the co-ordinate transformation1 the Hamiltonian may be written[17]: 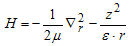 | (20) |
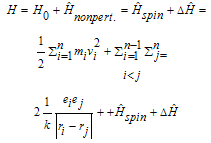 | (21) |
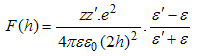 | (22) |
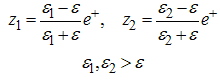 | (23) |
3. Four-particle Spin Interaction in Quantum Dots
- As we know all Hamilton of particles should be determined through surveying spin-spin and spin-orbital effect between particles in quantum dots. So final potential in quantum dots will be equal to vector potential resulted from uni-photon transaction and the potential resulted from electrons’ confinement and spin effect: (complementary Hamilton’s effect (
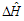 ) and relative potential (
) and relative potential (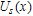 )have been omitted due to simplicity):
)have been omitted due to simplicity):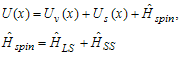 | (24) |
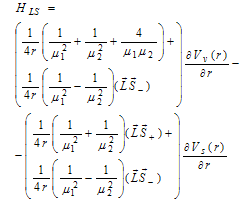 | (25) |
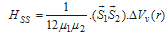 | (26) |
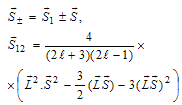 | (27) |
|
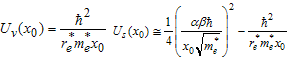 | (28) |
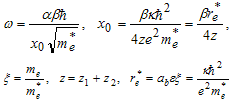 Where
Where 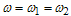 -oscillator frequency of electrons and
-oscillator frequency of electrons and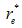 - is effective radius of system. In 1991, Schoberl-Louch-Gromes[22], found spin-orbital equations, while these equations are in force for quantum points and we will use them here. Suppose
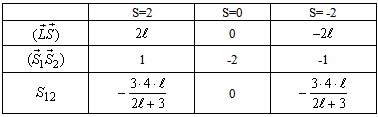
- is effective radius of system. In 1991, Schoberl-Louch-Gromes[22], found spin-orbital equations, while these equations are in force for quantum points and we will use them here. Suppose 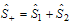 for sum of two electrons’ spin in diexciton, and for spin-orbital and spin-spin equations we will have:
for sum of two electrons’ spin in diexciton, and for spin-orbital and spin-spin equations we will have: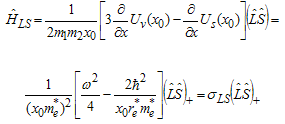 | (29) |
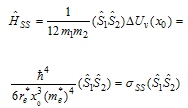 | (30) |
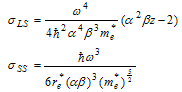 | (31) |
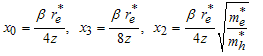 | (32) |
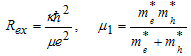 | (33) |
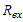 - Bohr radius of exciton or relative distance between electron and hole,
- Bohr radius of exciton or relative distance between electron and hole, 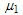 - constituent mass of exciton system,
- constituent mass of exciton system, 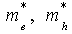 - effective mass of electron and hold. Relation of exciton radius resulted from Wannier equation in homogeneous environment with
- effective mass of electron and hold. Relation of exciton radius resulted from Wannier equation in homogeneous environment with 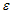 dielectric constant coefficient and exciton radius founded for quantum dots between inhomogeneous environments with the same constant dielectric coefficient
dielectric constant coefficient and exciton radius founded for quantum dots between inhomogeneous environments with the same constant dielectric coefficient 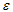 in oscillator method is:
in oscillator method is: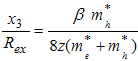 | (34) |
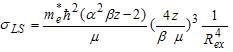 | (35) |
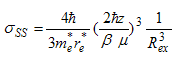 | (36) |
4. Conclusions
- In this study we worked on spin effects in Nano-crystals constructed by diexciton system in space between
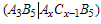 nanostructures. Oscillating calculation method has been used to calculate this effect and results of moving form general coordination to Jacobean coordination have been fully discussed. The method based on the investigation of the asymptotic behavior of the polarization loop function for diexciton in an external electro-magnetic field and oscillator representation method. We determined the spin-orbital interaction Hamiltonian with the relativistic corrections and defined spin-spin and spin-orbital Hamilton constant coefficient.In addition we have shown that how spin Hamiltonian constant coefficients
nanostructures. Oscillating calculation method has been used to calculate this effect and results of moving form general coordination to Jacobean coordination have been fully discussed. The method based on the investigation of the asymptotic behavior of the polarization loop function for diexciton in an external electro-magnetic field and oscillator representation method. We determined the spin-orbital interaction Hamiltonian with the relativistic corrections and defined spin-spin and spin-orbital Hamilton constant coefficient.In addition we have shown that how spin Hamiltonian constant coefficients 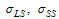 of exciton system between inhomogeneous environments are related to exciton radius of homogeneous environment. Diagrams for some of nanostructures show that spin effect increase with increase of visual charges (z), and get to steep slop along decrease in dielectric relative coefficient in potential well and electron distance decreases due to their confinement in quantum dot along with increase of visual charges (z).
of exciton system between inhomogeneous environments are related to exciton radius of homogeneous environment. Diagrams for some of nanostructures show that spin effect increase with increase of visual charges (z), and get to steep slop along decrease in dielectric relative coefficient in potential well and electron distance decreases due to their confinement in quantum dot along with increase of visual charges (z).Appendix
- The important point of calculations is the definition of Hamiltonian's structure of interaction. Interactions between composite particles are carried out through interchanging of gauge fields, therefore the propagator we shall note in a standard way:
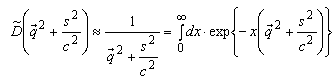 | (A.1) |
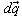 we have[25]:
we have[25]: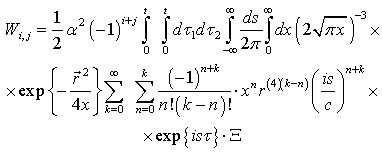 | (A.2) |
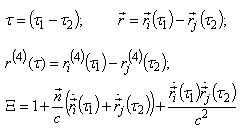 | (A.3) |
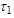 and
and 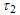 - is considered as proper time particles 1 and 2. We suppose that in initial moment particle rest and interact among themselves only by electric field. In this case we have
- is considered as proper time particles 1 and 2. We suppose that in initial moment particle rest and interact among themselves only by electric field. In this case we have 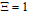 . On the other hand, we consider that
. On the other hand, we consider that 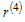 - Euclid time is connected with
- Euclid time is connected with 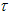 - proper time quarks as follows:
- proper time quarks as follows: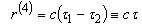 | (A4) |
 | (A.5) |
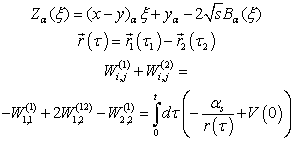 | (A.6) |
Notes
- 1Jacobian transformation.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML