S. Sh. Rekhviashvili1, 2, D. Sh. Gavasheli1
1Research Institute of Applied Mathematics and Automation of the Kabardino-Balkarian Research Center of the Russian Academy of Sciences, Nalchik , Russia
2Kabardino-Balkarian State University, Nalchik , Russia
Correspondence to: S. Sh. Rekhviashvili, Research Institute of Applied Mathematics and Automation of the Kabardino-Balkarian Research Center of the Russian Academy of Sciences, Nalchik , Russia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The nonlinear partial differential equation which describes heating of dielectric materials with fractal structure under the influence of pulse laser beam is received. The known equations from literature can be considered as special cases of the obtained equation. Fractality is considered in calculations of thermal conductivity coefficient, isochoric heat capacity and intensity of substance thermal radiation. The numerical decision of the equation is received. It is shown that the fractal properties of dielectric solid can essentially influence in heating process.
Keywords:
solid states, fractal dimensionality, thermal properties, laser beam and heating
Cite this paper: S. Sh. Rekhviashvili, D. Sh. Gavasheli, Modeling of Laser Pulse Heating of Solid Dielectric with a Fractal Structure, American Journal of Condensed Matter Physics, Vol. 2 No. 2, 2012, pp. 53-56. doi: 10.5923/j.ajcmp.20120202.03.
1. Introduction
Absorption of laser radiation occurs at exposure to laser radiation on matter. This process is directly related to the dielectric properties of matter and causes the heating and phase transitions. It is believed that the destruction of an optically transparent dielectric material by laser radiation is often precisely thermal nature[1]. Process of a laser heating of various solid bodies up to them destruction has the thermal nature is more often[2].Dielectric materials with fractal structure have a great fundamental and applied interest. It is enough to mention that many polymers, ceramic compounds and carbon nanocomposites fall into such materials. Investigation of thermal and optical properties of these materials is important in technology of thin film coating for energy-saving technologies, electronics and medicine. Various questions of thermophysics of fractals were discussed in works[3-5].Heating of non-polar dielectrics is caused, mainly, by phonons transfer and is described by partial differential equations of parabolic type[6]. These equations are sometimes modified using the fractional integro-differentiation[7] to simulate the heating of fractal structures which, however, involves considerable mathematical difficulties.In this paper we propose simple model of heating of solid dielectric solid state. The physical approach based on nonlinear partial differential equation. The fractal properties of material are considered in the calculation of radiative energy losses and thermal conductivity coefficient depending on temperature which leads to a nonlinear heat equation.
2. Physical Characteristics of Solid Dielectric Fractals
Consider the important physical characteristics of the sample depending on the fractal structure. In the work[8] was obtained expression for the isochoric heat capacity which we here write in the form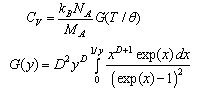 | (1) |
where D is the spectral fractal dimensionality, 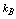 and
and 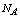 are the Boltzmann and Avogadro constants,
are the Boltzmann and Avogadro constants, 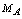 is the molar mass, T and
is the molar mass, T and 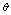 are the absolute and characteristic temperatures. The thermal conductivity coefficient in the quantum statistical approach can be written[9]:
are the absolute and characteristic temperatures. The thermal conductivity coefficient in the quantum statistical approach can be written[9]: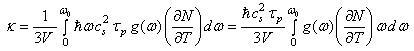 | (2) |
where 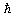 is the Planck's constant,
is the Planck's constant, 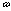 is the phonons frequency,
is the phonons frequency, 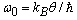 is the characteristic frequency,
is the characteristic frequency, 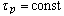 is the mean free time of phonons, V is the molar volume,
is the mean free time of phonons, V is the molar volume, 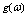 is the phonon states density,
is the phonon states density, 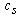 is the speed of sound and N is the number of phonons. Using the Bose-Einstein distribution and the expression for the phonon states density[8] from equation (2) we find
is the speed of sound and N is the number of phonons. Using the Bose-Einstein distribution and the expression for the phonon states density[8] from equation (2) we find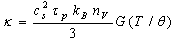 | (3) |
where 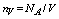 is the volume concentration of atoms.During the heating of sample by laser beam the quantity of absorbed energy should be spent on thermal radiation. The substance will continuously cool by radiative energy losses even in the absence of convective heat transfer. We calculate the integrated intensity of thermal radiation to take into account this mechanism. For this we use the familiar expression:
is the volume concentration of atoms.During the heating of sample by laser beam the quantity of absorbed energy should be spent on thermal radiation. The substance will continuously cool by radiative energy losses even in the absence of convective heat transfer. We calculate the integrated intensity of thermal radiation to take into account this mechanism. For this we use the familiar expression: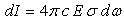 | (4) |
where c is the speed of light in a vacuum, 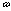 is the frequency of radiation,
is the frequency of radiation, 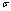 is the photon absorption cross sections,
is the photon absorption cross sections, 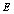 is the spectral density of blackbody radiation per unit volume and unit solid angle interval. The absorption cross section of some dielectric body having volume
is the spectral density of blackbody radiation per unit volume and unit solid angle interval. The absorption cross section of some dielectric body having volume 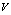 is given by[10]:
is given by[10]: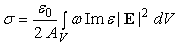 | (5) |
where 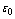 is the permittivity of free space,
is the permittivity of free space, 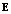 is the electric field vector, A is the amplitude of the flux vector of the incident wave power density,
is the electric field vector, A is the amplitude of the flux vector of the incident wave power density, 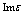 is the imaginary part of dielectric function which characterizes the absorption of radiation.If the size of a single fractal cluster smaller than the wavelength of the incident radiation we can assume that the boundary conditions for electromagnetic wave coincides with the boundary conditions for solid particles. That is some averaging of the polarizability and the cluster behaves as isotropic with a density and dielectric properties depending on the fractal dimensionality. If we accept
is the imaginary part of dielectric function which characterizes the absorption of radiation.If the size of a single fractal cluster smaller than the wavelength of the incident radiation we can assume that the boundary conditions for electromagnetic wave coincides with the boundary conditions for solid particles. That is some averaging of the polarizability and the cluster behaves as isotropic with a density and dielectric properties depending on the fractal dimensionality. If we accept 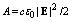 and make allowance for that integrand in (5) does not depend on the volume we get
and make allowance for that integrand in (5) does not depend on the volume we get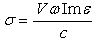 | (6) |
For Planck distribution we have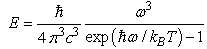 | (7) |
Substituting (6), (7) in (4), we find the total intensity of radiation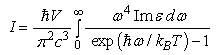 | (8) |
We note that the integral in (8) diverges if at low frequencies the imaginary component of the dielectric function has a power asymptotic and tends to infinity faster than 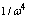 .The specific properties dealing with the frequency dispersion of polarization and dielectric function are characteristic of polymers, composite materials and glasses having fractal structure. For the description of complex dielectric susceptibility and, accordingly, complex permittivity of these materials is commonly used Cole-Cole, Cole-Davidson and Havriliak-Negami formulas[11]. The adequacy of these equations has been confirmed repeatedly by experiments on the dielectric and capacitance spectroscopy, nuclear magnetic resonance, neutron scattering. The Havriliak-Negami complex dielectric function has a most general view:
.The specific properties dealing with the frequency dispersion of polarization and dielectric function are characteristic of polymers, composite materials and glasses having fractal structure. For the description of complex dielectric susceptibility and, accordingly, complex permittivity of these materials is commonly used Cole-Cole, Cole-Davidson and Havriliak-Negami formulas[11]. The adequacy of these equations has been confirmed repeatedly by experiments on the dielectric and capacitance spectroscopy, nuclear magnetic resonance, neutron scattering. The Havriliak-Negami complex dielectric function has a most general view: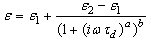 | (9) |
where a and b are the semi-empirical parameters taken into account the fractal structure implicitly, 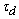 is the dielectric relaxation time,
is the dielectric relaxation time, 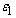 and
and 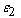 are the high-frequency and low-frequency dielectric permittivity (
are the high-frequency and low-frequency dielectric permittivity (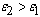 ). Expression (9) describes of Debye dielectric relaxation processes at
). Expression (9) describes of Debye dielectric relaxation processes at 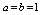 , Cole-Cole at
, Cole-Cole at 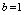 and Cole-Davidson at
and Cole-Davidson at 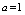 as a frequent cases. The imaginary part of (9) is
as a frequent cases. The imaginary part of (9) is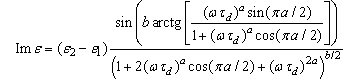 | (10) |
where it has been taken into account that 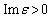 . After substituting (10) into (8) and subsequent integration with the condition
. After substituting (10) into (8) and subsequent integration with the condition 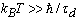 we find
we find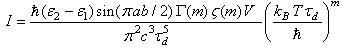 | (11) |
where 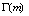 and
and 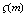 are the gamma function and Riemann zeta function,
are the gamma function and Riemann zeta function, 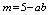 . The radiation intensity becomes power function of temperature with noninteger index. This function is characteristic of many physical processes in the presence of self-similarity and fractality. It is pertinent to note that the power-temperature dependence with fractional exponents appear in fractal Debay theory of solid state heat capacity[8].
. The radiation intensity becomes power function of temperature with noninteger index. This function is characteristic of many physical processes in the presence of self-similarity and fractality. It is pertinent to note that the power-temperature dependence with fractional exponents appear in fractal Debay theory of solid state heat capacity[8].
3. Laser Heating Modeling
Let us consider the following processes in the modeling of heating: 1) the absorption of laser radiation, 2) reflection of the laser radiation from the surface, 3) thermal radiation from the heated sample. Convective heat exchange with the surrounding space is not considered. This is true if the irradiation of the material is carried out in vacuum conditions. Convective heat exchange at the experiments in air with laser pulses of short duration is also negligible due to low heat. Under the condition of (1), (3), (11), as well as Beer-Lambert-Bouguer law the one-dimensional heat conduction equation takes the form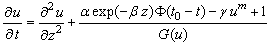 | (12) |
where 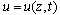 is the dimensionless (referred to the Debye temperature) temperature, t and z are the dimensionless time and coordinate,
is the dimensionless (referred to the Debye temperature) temperature, t and z are the dimensionless time and coordinate, 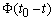 is the Heaviside function which simulates a laser pulse duration of
is the Heaviside function which simulates a laser pulse duration of 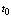 . The dimensionless parameters in equation (12) are
. The dimensionless parameters in equation (12) are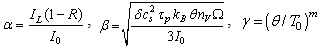 | (13) |
where 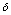 and R are the coefficients of absorption and reflection of laser radiation,
and R are the coefficients of absorption and reflection of laser radiation, 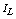 is the intensity of the laser beam, Ω is the effective area of fractal dielectric surface,
is the intensity of the laser beam, Ω is the effective area of fractal dielectric surface, 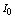 is the intensity of thermal radiation calculated by formula (11) at ambient temperature
is the intensity of thermal radiation calculated by formula (11) at ambient temperature 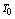 . Time and coordinate in equation (12) attributed to the following dimensional constants respectively:
. Time and coordinate in equation (12) attributed to the following dimensional constants respectively: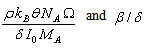 .Writing equation (12) we was also assumed that the fractal matter volume varies slightly at heating, so
.Writing equation (12) we was also assumed that the fractal matter volume varies slightly at heating, so 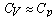 , where
, where 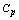 is the isobaric heat capacity. In order to simplify the equation (12) the term containing was
is the isobaric heat capacity. In order to simplify the equation (12) the term containing was 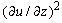 ruled out also. From a physical point of view it is justified only at high temperatures; according to the results obtained above (the formula (3) at
ruled out also. From a physical point of view it is justified only at high temperatures; according to the results obtained above (the formula (3) at 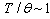 ) thermal conductivity coefficient at high temperatures varies slightly so that the derivative
) thermal conductivity coefficient at high temperatures varies slightly so that the derivative 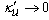 .We assume that the same temperature is maintained at the ends of the irradiated sample which is equal to the ambient temperature:
.We assume that the same temperature is maintained at the ends of the irradiated sample which is equal to the ambient temperature: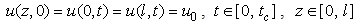 | (14) |
where 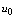 and l are the determine the ambient temperature and the linear size of the sample respectively,
and l are the determine the ambient temperature and the linear size of the sample respectively, 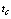 is the calculation time. To be of interest to consider two cases separately at numerical modeling:
is the calculation time. To be of interest to consider two cases separately at numerical modeling: 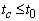 and
and 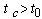 .The nonlinear equation (12) together with (14) can not be solved analytically so it is interesting to consider one special case. We assume that the thin surface layer heat (
.The nonlinear equation (12) together with (14) can not be solved analytically so it is interesting to consider one special case. We assume that the thin surface layer heat (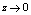 ). In this case from the equation (12) at the high temperatures (
). In this case from the equation (12) at the high temperatures (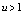 ,
,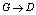 ) and with account of Debye relaxation (
) and with account of Debye relaxation (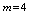 ) we obtain
) we obtain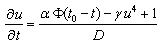 | (15) |
Within the laser pulse action at 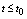 equation (15) is solved by method of separation of variables
equation (15) is solved by method of separation of variables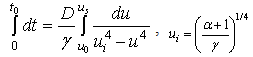 | (16) |
where 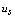 is the maximum temperature, which is set in a time
is the maximum temperature, which is set in a time 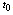 . Carrying out the integration in (16) we obtain
. Carrying out the integration in (16) we obtain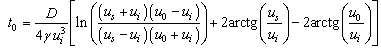 | (17) |
If radiation heat exchange can be neglected then the solution (17) is simplified to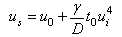 | (18) |
If we also neglect the ambient temperature and make transition to dimensional quantities then equation (18) leads to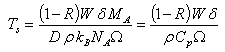 | (19) |
where W=ILt0Ω is the laser energy, 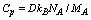 is the isobaric heat capacity corresponding to the generalized law of Dulong-Petit[5]. Formula (19) allows us to estimate approximately the temperature of the sample surface which is installed as a result of pulsed laser irradiation.Computing experiment was carried out by means of MathCad program. Built-in operator Pdesolve was used to solve the boundary problem (14) for equation (12). Figures 1-6 shows some dependencies which were calculated to demonstrate the influence of physical parameters of a fractal solid body on the process of laser pulse heating. Each pair of figures relates to a change in a one selected parameter (it is indicated above) at fixed values of other parameters (they are indicated below.). Estimates show that the limiting value of the relative temperature
is the isobaric heat capacity corresponding to the generalized law of Dulong-Petit[5]. Formula (19) allows us to estimate approximately the temperature of the sample surface which is installed as a result of pulsed laser irradiation.Computing experiment was carried out by means of MathCad program. Built-in operator Pdesolve was used to solve the boundary problem (14) for equation (12). Figures 1-6 shows some dependencies which were calculated to demonstrate the influence of physical parameters of a fractal solid body on the process of laser pulse heating. Each pair of figures relates to a change in a one selected parameter (it is indicated above) at fixed values of other parameters (they are indicated below.). Estimates show that the limiting value of the relative temperature 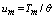 at which there is melting is located in a sufficient narrow range from 2 to 2.5 for some dielectrics (quartz, sapphire, ruby, diamond). Therefore, the intensity of laser radiation in the simulation of heating should be selected in accordance with the condition
at which there is melting is located in a sufficient narrow range from 2 to 2.5 for some dielectrics (quartz, sapphire, ruby, diamond). Therefore, the intensity of laser radiation in the simulation of heating should be selected in accordance with the condition 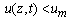 . Initial data for all considered cases had the following values
. Initial data for all considered cases had the following values 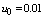 ,
, 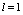 and
and 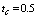 .Fig. 1 shows that increasing of laser radiation intensity leads to increase of temperature and to reducing transition time of heating. Laser radiation absorption at the initial moments of time causes a nonuniform temperature profile and increases the time of onset of the stationary mode of heating as shown in Fig. 2. The results of modeling presented in Fig. 3 show that the sample can cool down effectively due to radiation heat exchange. In the transition from frequency independent dielectric to the complex permittivity described by Havriliak-Negami equation (9) the exponent m in the temperature dependence of the intensity of thermal radiation varies from 5 to 4. Similar change leads to a slight increase in heating temperature (Fig. 4). In low-dimensional systems atoms or molecules are connected to each other weakly and therefore more mobile. For this reason reduction of the fractal dimensionality leads to an increase in temperature as illustrated in Fig. 5. In addition, taking into account the dependence
.Fig. 1 shows that increasing of laser radiation intensity leads to increase of temperature and to reducing transition time of heating. Laser radiation absorption at the initial moments of time causes a nonuniform temperature profile and increases the time of onset of the stationary mode of heating as shown in Fig. 2. The results of modeling presented in Fig. 3 show that the sample can cool down effectively due to radiation heat exchange. In the transition from frequency independent dielectric to the complex permittivity described by Havriliak-Negami equation (9) the exponent m in the temperature dependence of the intensity of thermal radiation varies from 5 to 4. Similar change leads to a slight increase in heating temperature (Fig. 4). In low-dimensional systems atoms or molecules are connected to each other weakly and therefore more mobile. For this reason reduction of the fractal dimensionality leads to an increase in temperature as illustrated in Fig. 5. In addition, taking into account the dependence 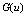 in equation (12) considerably reduces the steady-state mode of heating. Fig. 6 shows that the activity of laser radiation during a finite period of time
in equation (12) considerably reduces the steady-state mode of heating. Fig. 6 shows that the activity of laser radiation during a finite period of time 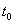 leads to a heat pulse in the sample. At the same time rising and falling edges of this pulse is blurred due to unsteady heating and cooling processes.
leads to a heat pulse in the sample. At the same time rising and falling edges of this pulse is blurred due to unsteady heating and cooling processes.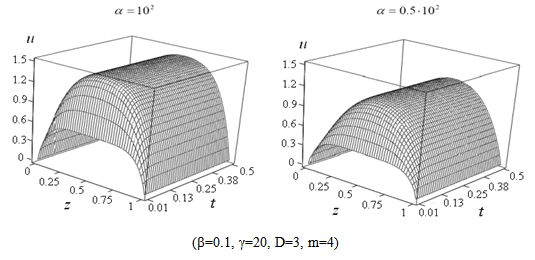 | Figure 1. Influence of laser intensity on heating |
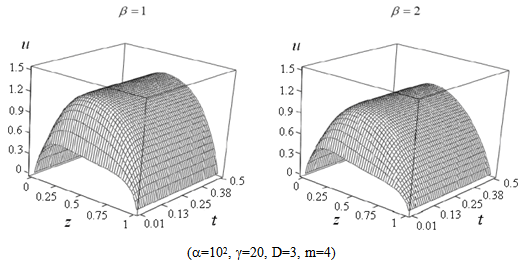 | Figure 2. Influence of laser radiation absorption on heating |
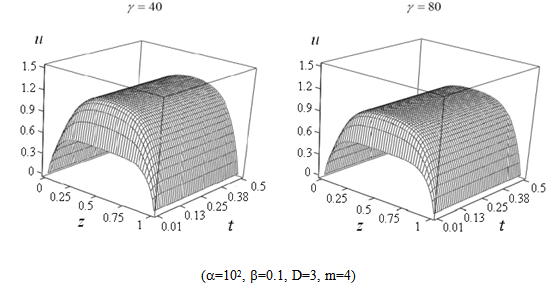 | Figure 3. Influence of radiative heat exchange intensity on heating |
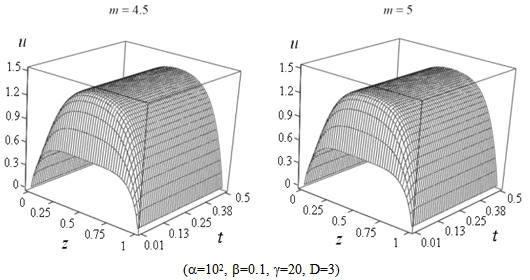 | Figure 4. Influence of dielectric function parameters on heating |
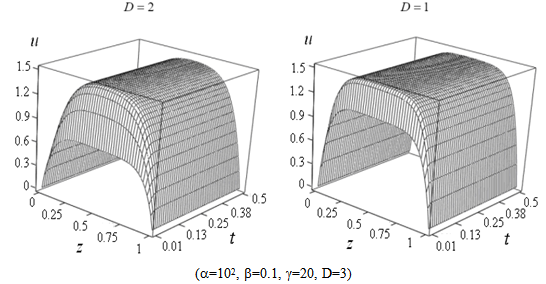 | Figure 5. Influence of phonon (spectral) fractal dimensionality on heating |
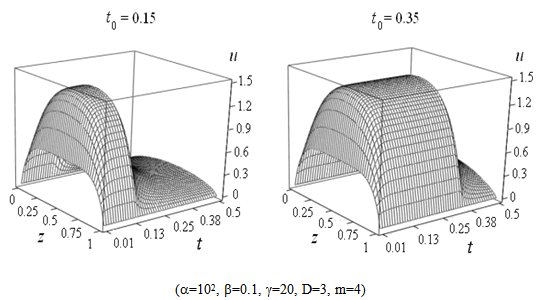 | Figure 6. Influence of finite laser pulse duration on heating |
4. Conclusions
Materials with fractal structure are varied physical and chemical properties that make them promising in real structures. We have implemented a comprehensive approach to the analysis of thermal kinetics processes in dielectric fractal solids. The model is valid in the absence of gas-dynamic effects and effects associated with the ionization and plasma formation. In present paper the following conclusions were formulated: 1) analytical expressions for the intensity of thermal radiation and thermal conductivity coefficient of dielectric fractal materials are obtained, 2) numerical solution of the heat equation shows that the fractal properties of the sample can significantly affect the heating process.
References
| [1] | B. C. Stuart, M. D. Feit, S. Herman, A. M. Rubenchik, B. W. Shore, M. D. Perry, Journal of the Optical Society of America B 13 (1996) 459. |
| [2] | R. M. Wood, Laser-induced damage of optical materials, Institute of Physics Publishing Bristol and Philadelphia, 2003. |
| [3] | Xiulan Huaia, Weiwei Wanga, Zhigang Lia, Applied Thermal Engineering 27 (2007) 2815. |
| [4] | P.E. Gharagozloo, K.E. Goodson, Journal of Applied Physics 108 (2010) 074309. |
| [5] | Yijiang Wang, Guoqing Zhou, Yazhi Wei, Yang Zhou, Mining Science and Technology (China) 20 (2010) 831. |
| [6] | H. S. Carslaw, J. C. Jaeger, Conduction of heat in solids, Oxford University, 1959. |
| [7] | I. Podlubny, Fractional differential equations. An introduction to fractional derivatives, fractional differential equations, some methods of their solution and some of their applications, Academic Press, San Diego-Boston-New York-London-Tokyo-Toronto, 1999. |
| [8] | S. Sh. Rekhviashvili, Technical Physics Letters 30 (2004) 959 |
| [9] | J. R. Drabble, H. J. Goldsmid, Thermal conduction in semiconductors, Pergamon Press, Oxford, 1961. |
| [10] | A. Ishimaru, Wave propagation and scattering in random media, Academic Press New York, 1978. |
| [11] | T. Blythe, D. Bloor, Electrical properties of polymers, Cambridge, 2005. |

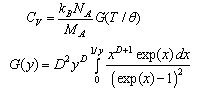
 and
and  are the Boltzmann and Avogadro constants,
are the Boltzmann and Avogadro constants, 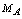 is the molar mass, T and
is the molar mass, T and 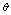 are the absolute and characteristic temperatures. The thermal conductivity coefficient in the quantum statistical approach can be written[9]:
are the absolute and characteristic temperatures. The thermal conductivity coefficient in the quantum statistical approach can be written[9]: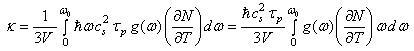
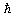 is the Planck's constant,
is the Planck's constant, 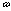 is the phonons frequency,
is the phonons frequency, 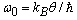 is the characteristic frequency,
is the characteristic frequency, 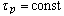 is the mean free time of phonons, V is the molar volume,
is the mean free time of phonons, V is the molar volume, 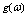 is the phonon states density,
is the phonon states density, 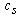 is the speed of sound and N is the number of phonons. Using the Bose-Einstein distribution and the expression for the phonon states density[8] from equation (2) we find
is the speed of sound and N is the number of phonons. Using the Bose-Einstein distribution and the expression for the phonon states density[8] from equation (2) we find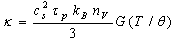
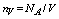 is the volume concentration of atoms.During the heating of sample by laser beam the quantity of absorbed energy should be spent on thermal radiation. The substance will continuously cool by radiative energy losses even in the absence of convective heat transfer. We calculate the integrated intensity of thermal radiation to take into account this mechanism. For this we use the familiar expression:
is the volume concentration of atoms.During the heating of sample by laser beam the quantity of absorbed energy should be spent on thermal radiation. The substance will continuously cool by radiative energy losses even in the absence of convective heat transfer. We calculate the integrated intensity of thermal radiation to take into account this mechanism. For this we use the familiar expression: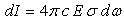
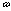 is the frequency of radiation,
is the frequency of radiation, 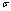 is the photon absorption cross sections,
is the photon absorption cross sections, 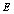 is the spectral density of blackbody radiation per unit volume and unit solid angle interval. The absorption cross section of some dielectric body having volume
is the spectral density of blackbody radiation per unit volume and unit solid angle interval. The absorption cross section of some dielectric body having volume 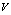 is given by[10]:
is given by[10]: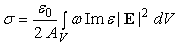
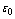 is the permittivity of free space,
is the permittivity of free space, 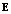 is the electric field vector, A is the amplitude of the flux vector of the incident wave power density,
is the electric field vector, A is the amplitude of the flux vector of the incident wave power density, 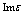 is the imaginary part of dielectric function which characterizes the absorption of radiation.If the size of a single fractal cluster smaller than the wavelength of the incident radiation we can assume that the boundary conditions for electromagnetic wave coincides with the boundary conditions for solid particles. That is some averaging of the polarizability and the cluster behaves as isotropic with a density and dielectric properties depending on the fractal dimensionality. If we accept
is the imaginary part of dielectric function which characterizes the absorption of radiation.If the size of a single fractal cluster smaller than the wavelength of the incident radiation we can assume that the boundary conditions for electromagnetic wave coincides with the boundary conditions for solid particles. That is some averaging of the polarizability and the cluster behaves as isotropic with a density and dielectric properties depending on the fractal dimensionality. If we accept 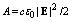 and make allowance for that integrand in (5) does not depend on the volume we get
and make allowance for that integrand in (5) does not depend on the volume we get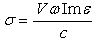
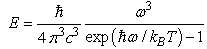
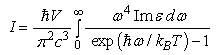
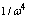 .The specific properties dealing with the frequency dispersion of polarization and dielectric function are characteristic of polymers, composite materials and glasses having fractal structure. For the description of complex dielectric susceptibility and, accordingly, complex permittivity of these materials is commonly used Cole-Cole, Cole-Davidson and Havriliak-Negami formulas[11]. The adequacy of these equations has been confirmed repeatedly by experiments on the dielectric and capacitance spectroscopy, nuclear magnetic resonance, neutron scattering. The Havriliak-Negami complex dielectric function has a most general view:
.The specific properties dealing with the frequency dispersion of polarization and dielectric function are characteristic of polymers, composite materials and glasses having fractal structure. For the description of complex dielectric susceptibility and, accordingly, complex permittivity of these materials is commonly used Cole-Cole, Cole-Davidson and Havriliak-Negami formulas[11]. The adequacy of these equations has been confirmed repeatedly by experiments on the dielectric and capacitance spectroscopy, nuclear magnetic resonance, neutron scattering. The Havriliak-Negami complex dielectric function has a most general view: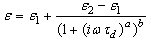
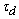 is the dielectric relaxation time,
is the dielectric relaxation time, 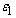 and
and 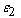 are the high-frequency and low-frequency dielectric permittivity (
are the high-frequency and low-frequency dielectric permittivity (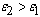 ). Expression (9) describes of Debye dielectric relaxation processes at
). Expression (9) describes of Debye dielectric relaxation processes at 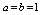 , Cole-Cole at
, Cole-Cole at 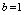 and Cole-Davidson at
and Cole-Davidson at 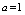 as a frequent cases. The imaginary part of (9) is
as a frequent cases. The imaginary part of (9) is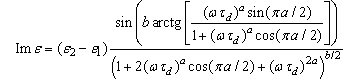
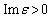 . After substituting (10) into (8) and subsequent integration with the condition
. After substituting (10) into (8) and subsequent integration with the condition 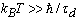 we find
we find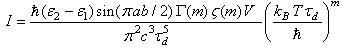
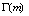 and
and 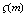 are the gamma function and Riemann zeta function,
are the gamma function and Riemann zeta function, 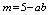 . The radiation intensity becomes power function of temperature with noninteger index. This function is characteristic of many physical processes in the presence of self-similarity and fractality. It is pertinent to note that the power-temperature dependence with fractional exponents appear in fractal Debay theory of solid state heat capacity[8].
. The radiation intensity becomes power function of temperature with noninteger index. This function is characteristic of many physical processes in the presence of self-similarity and fractality. It is pertinent to note that the power-temperature dependence with fractional exponents appear in fractal Debay theory of solid state heat capacity[8].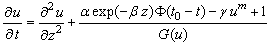
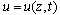 is the dimensionless (referred to the Debye temperature) temperature, t and z are the dimensionless time and coordinate,
is the dimensionless (referred to the Debye temperature) temperature, t and z are the dimensionless time and coordinate, 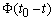 is the Heaviside function which simulates a laser pulse duration of
is the Heaviside function which simulates a laser pulse duration of 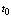 . The dimensionless parameters in equation (12) are
. The dimensionless parameters in equation (12) are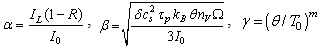
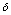 and R are the coefficients of absorption and reflection of laser radiation,
and R are the coefficients of absorption and reflection of laser radiation, 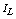 is the intensity of the laser beam, Ω is the effective area of fractal dielectric surface,
is the intensity of the laser beam, Ω is the effective area of fractal dielectric surface, 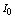 is the intensity of thermal radiation calculated by formula (11) at ambient temperature
is the intensity of thermal radiation calculated by formula (11) at ambient temperature 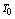 . Time and coordinate in equation (12) attributed to the following dimensional constants respectively:
. Time and coordinate in equation (12) attributed to the following dimensional constants respectively: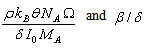 .Writing equation (12) we was also assumed that the fractal matter volume varies slightly at heating, so
.Writing equation (12) we was also assumed that the fractal matter volume varies slightly at heating, so 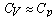 , where
, where 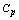 is the isobaric heat capacity. In order to simplify the equation (12) the term containing was
is the isobaric heat capacity. In order to simplify the equation (12) the term containing was 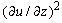 ruled out also. From a physical point of view it is justified only at high temperatures; according to the results obtained above (the formula (3) at
ruled out also. From a physical point of view it is justified only at high temperatures; according to the results obtained above (the formula (3) at 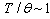 ) thermal conductivity coefficient at high temperatures varies slightly so that the derivative
) thermal conductivity coefficient at high temperatures varies slightly so that the derivative 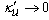 .We assume that the same temperature is maintained at the ends of the irradiated sample which is equal to the ambient temperature:
.We assume that the same temperature is maintained at the ends of the irradiated sample which is equal to the ambient temperature: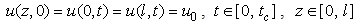
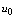 and l are the determine the ambient temperature and the linear size of the sample respectively,
and l are the determine the ambient temperature and the linear size of the sample respectively, 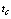 is the calculation time. To be of interest to consider two cases separately at numerical modeling:
is the calculation time. To be of interest to consider two cases separately at numerical modeling: 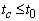 and
and 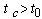 .The nonlinear equation (12) together with (14) can not be solved analytically so it is interesting to consider one special case. We assume that the thin surface layer heat (
.The nonlinear equation (12) together with (14) can not be solved analytically so it is interesting to consider one special case. We assume that the thin surface layer heat (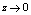 ). In this case from the equation (12) at the high temperatures (
). In this case from the equation (12) at the high temperatures (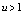 ,
,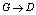 ) and with account of Debye relaxation (
) and with account of Debye relaxation (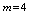 ) we obtain
) we obtain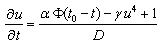
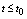 equation (15) is solved by method of separation of variables
equation (15) is solved by method of separation of variables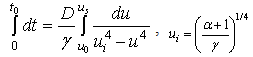
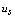 is the maximum temperature, which is set in a time
is the maximum temperature, which is set in a time 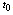 . Carrying out the integration in (16) we obtain
. Carrying out the integration in (16) we obtain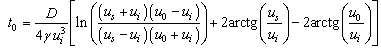
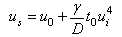
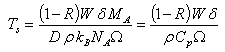
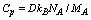 is the isobaric heat capacity corresponding to the generalized law of Dulong-Petit[5]. Formula (19) allows us to estimate approximately the temperature of the sample surface which is installed as a result of pulsed laser irradiation.Computing experiment was carried out by means of MathCad program. Built-in operator Pdesolve was used to solve the boundary problem (14) for equation (12). Figures 1-6 shows some dependencies which were calculated to demonstrate the influence of physical parameters of a fractal solid body on the process of laser pulse heating. Each pair of figures relates to a change in a one selected parameter (it is indicated above) at fixed values of other parameters (they are indicated below.). Estimates show that the limiting value of the relative temperature
is the isobaric heat capacity corresponding to the generalized law of Dulong-Petit[5]. Formula (19) allows us to estimate approximately the temperature of the sample surface which is installed as a result of pulsed laser irradiation.Computing experiment was carried out by means of MathCad program. Built-in operator Pdesolve was used to solve the boundary problem (14) for equation (12). Figures 1-6 shows some dependencies which were calculated to demonstrate the influence of physical parameters of a fractal solid body on the process of laser pulse heating. Each pair of figures relates to a change in a one selected parameter (it is indicated above) at fixed values of other parameters (they are indicated below.). Estimates show that the limiting value of the relative temperature 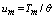 at which there is melting is located in a sufficient narrow range from 2 to 2.5 for some dielectrics (quartz, sapphire, ruby, diamond). Therefore, the intensity of laser radiation in the simulation of heating should be selected in accordance with the condition
at which there is melting is located in a sufficient narrow range from 2 to 2.5 for some dielectrics (quartz, sapphire, ruby, diamond). Therefore, the intensity of laser radiation in the simulation of heating should be selected in accordance with the condition 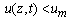 . Initial data for all considered cases had the following values
. Initial data for all considered cases had the following values 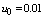 ,
, 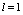 and
and 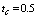 .Fig. 1 shows that increasing of laser radiation intensity leads to increase of temperature and to reducing transition time of heating. Laser radiation absorption at the initial moments of time causes a nonuniform temperature profile and increases the time of onset of the stationary mode of heating as shown in Fig. 2. The results of modeling presented in Fig. 3 show that the sample can cool down effectively due to radiation heat exchange. In the transition from frequency independent dielectric to the complex permittivity described by Havriliak-Negami equation (9) the exponent m in the temperature dependence of the intensity of thermal radiation varies from 5 to 4. Similar change leads to a slight increase in heating temperature (Fig. 4). In low-dimensional systems atoms or molecules are connected to each other weakly and therefore more mobile. For this reason reduction of the fractal dimensionality leads to an increase in temperature as illustrated in Fig. 5. In addition, taking into account the dependence
.Fig. 1 shows that increasing of laser radiation intensity leads to increase of temperature and to reducing transition time of heating. Laser radiation absorption at the initial moments of time causes a nonuniform temperature profile and increases the time of onset of the stationary mode of heating as shown in Fig. 2. The results of modeling presented in Fig. 3 show that the sample can cool down effectively due to radiation heat exchange. In the transition from frequency independent dielectric to the complex permittivity described by Havriliak-Negami equation (9) the exponent m in the temperature dependence of the intensity of thermal radiation varies from 5 to 4. Similar change leads to a slight increase in heating temperature (Fig. 4). In low-dimensional systems atoms or molecules are connected to each other weakly and therefore more mobile. For this reason reduction of the fractal dimensionality leads to an increase in temperature as illustrated in Fig. 5. In addition, taking into account the dependence 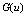 in equation (12) considerably reduces the steady-state mode of heating. Fig. 6 shows that the activity of laser radiation during a finite period of time
in equation (12) considerably reduces the steady-state mode of heating. Fig. 6 shows that the activity of laser radiation during a finite period of time 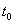 leads to a heat pulse in the sample. At the same time rising and falling edges of this pulse is blurred due to unsteady heating and cooling processes.
leads to a heat pulse in the sample. At the same time rising and falling edges of this pulse is blurred due to unsteady heating and cooling processes.





 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML