-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Condensed Matter Physics
p-ISSN: 2163-1115 e-ISSN: 2163-1123
2012; 2(2): 32-52
doi: 10.5923/j.ajcmp.20120202.02
Microscopic Theory of a System of Interacting Bosons-I : Basic Foundations and Superfluidity
Yatendra S. Jain
Department of Physics, North-Eastern Hill University, Shillong, 793022, India
Correspondence to: Yatendra S. Jain , Department of Physics, North-Eastern Hill University, Shillong, 793022, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Important aspects of a system of interacting bosons like liquid 4He are critically analyzed to lay down the basic foundations of a new approach to develop its microscopic theory that explains its properties at quantitative level. It is shown that each particle represents a pair of particles (identified as the basic unit of the system) having equal and opposite momenta (q,-q) with respect to their center of mass (CM) that moves as a free particle with momentum K; its quantum state is represented by a macro-orbital which ascribes a particle to have two motions (q and K) of the representative pair. While q is restricted to satisfy q ≥ qo = π/d (d being the nearest neighbor distance) due to hard core inter-particle interaction, K, having no such restriction, can have any value between 0 and ∞. In the ground state of the system, all particles have: (i) q = qo and K = 0, (ii) identically equal nearest neighbor distance r (= d), and (iii) relative phase positions locked at ∆φ (= 2q.r) = 2nπ (n = 1, 2, 3...); they define a close packed arrangement of their wave packets (CPA-WP) having identically equal size, λ/2 = d. The transition to superfluid state represents simultaneous onset of Bose Einstein condensation of particles in the state of q = qo and K = 0 and an order-disorder process which moves particles from their disordered positions in phase space (with ∆φ ≥ 2π in the high temperature phase) to an ordered positions defined by ∆φ = 2nπ (in the low temperature phase). Quantum correlation potentials play an important role in this process. Particles in the superfluid state cease to have relative motion. They develop a kind of collective binding energy (Eg(T)), identified as an energy gap between normal liquid state and superfluid state. These inferences help in understanding all significant properties of the superfluid state including loss of viscosity, quantized vortices, critical velocities, infinitely high thermal conductivity, thermo-mechanical and mechano-caloric effects, etc. at quantitative scale; however, this fact is demonstrated in detail, elsewhere.
Keywords: Superfluidity, Microscopic theory, BEC, He-4
Article Outline
1. Introduction
- Liquid 4He (LHe-4)[a system of interacting bosons (SIB)] exhibits an interesting and extensively investigated phase transition at Tλ = 2.17K[1-5]. While its high temperature (HT) phase (He-I) has properties of a normal liquid, the low temperature (LT) phase (He-II) assumes several unique properties such as superfluidity, -flow through narrow channels without resistance (i.e., viscosity, η = 0). For the last seventy five years, superfluidity of He-II has been in focus for its widely different experimental and theoretical studies because it serves as a testing ground for the impacts of the wave nature of particles at macroscopic level and this has been reflected by a large number of research papers on the related physics published every year.The observation of superfluidity of LHe-4[1] in 1938, gave great boost to its experimental and theoretical studies. Within a short period of about three years enough experimental results were available[3] for a phenomenological theory developed by Landau[6] which identified He-II as a homogeneous mixture of two fluids, i.e., superfluid (density ρs) and normal fluid (density ρn = ρ − ρs with ρ = total density of He-II) of different properties[7]; the theory is well known as Landau’s two fluid theory and it is elegantly discussed by Putterman[5]. Similarly, after a few more years Bogoliubov[8] reported his theory of a system of weakly interacting bosons as a most significant contribution towards the development of the microscopic theory of a SIB and concluded that the density of Bose Einstein condensate (BEC) (also known as zero momentum (p = 0) condensate[9, 10]) is depleted if the bosons have repulsive interaction and the depletion increases with the increase in its strength; this[8] rendered a reason to believe in London’s suggestion[11] that superfluidity of He-II originates from the existence of p = 0 condensate of 4He-atoms which was presumed to be an important basis for further developments in the theory of a SIB.London’s suggestion[11] was further strengthened by a series of papers by Feynman and his collaborators[12-16] published during 1952-58. Starting from the exact quantum mechanical partition function of LHe-4, Feynman[12] not only showed that: (i) strong repulsion between 4He-atoms does not change λ−transition qualitatively from BE- condensation, and (ii) the spectrum of the elementary excitations of He-II (as perceived by Landau[6] to develop his two fluid theory) has quantum mechanical basis[13-16] but also discovered the origin of quantum vortices and their relation with criticality of He-II for its flow under rotation and through narrow channels[15]. In addition, Cohen and Feynman[17] predicted that the amplitude of neutron inelastic scattering (NIS) from quasi-particle excitations of LHe-4 should be reasonably large and this was later proved to be true through experiment[4]. In a nut shell, these studies[12-17] made Landau’s two fluid theory[6] more meaningful because its phenomenological concepts of phonons and rotons, which determine ρn(T) and ρs(T ), were shown to have microscopic foundation.In what follows after[8] and[12-16], while the main objective of the theoretical studies of LHe-4 remained to: (i) formulate the relation for its excitation spectrum, E(Q), and (ii) calculate the amount of p = 0 condensate (i.e., the fraction of the total number of particles (N) in p = 0 state np=0(T) = Np=0(T)/N) in He-II, the experimental studies were aimed at: (i) finding the details of E(Q), (ii) confirming the presumed existence of p = 0 condensate and finding its magnitude and (iii) revealing other aspects of significance such as quantum vortices. To this effect, while Bogoliubov’s theory[8] emerged as the starting point for the development of the microscopic theory of a SIB by using perturbative approach and second quantization[18], Feynman’s work[12-16] laid the foundation for the application of variational approach of quantum theory[19] and path integrals to calculate different properties of a many body quantum system (MBQS). This motivated a large number of researchers to undertake theoretical study of LHe-4 by using different possible presumptions, approximations, trial functions, mathematical tools and computational techniques and encouraged many experimentalists to measure its different properties. The wealth of theoretical and experimental results, so generated, have been periodically reviewed and analyzed in large number of books and review articles. Here we refer some of them for their relevance to the present study. These are broadly related to: (i) the progress of microscopic understanding of a SIB[20-23], (ii) computer simulations of the properties of LHe-4[24], (iii) the values of np=0(T) in He-II[25-28], (iv) E(Q) of LHe-4[29-31], and (v) quantum vortices[32, 33]. The basic understanding of the subject, so developed, is also summarized elegantly in graduate level texts[34-36]. In what follows, the unique properties of He-II are understood in terms of two fluid theory[6] and/or Ψ−theory[37] with a touch of microscopic basis which correlates ρs(T) with np=0(T ) which is estimated to fall around 10% for He-II at T = 0[28]. However, this conclusion not only faces several unanswered questions[38] but also finds no unequivocal experimental support for the existence of the presumed p = 0 condensate in He-II, -as evident from a discussion by Glyde and Svensson[25], Sokol[28] and Leggett[39].Several research groups have been trying to revise our understanding of the superfluid state of a SIB, particularly, after the discovery of BEC in trapped dilute gases (TDG) and their detailed studies[40-42]. While some researchers[43-46] have been trying to establish the idea that the said state has a kind of generalized/composite condensate (p = 0 condensate + pair condensate + ..), others[47, 48] have been making their efforts to underline the condensation of Cooper type pairs only. Developments in these directions are reviewed, recently, in several articles, viz.,[49-51].As such, it is evident that the real form of condensate responsible for the superfluidity of a SIB is unclear and a microscopic theory which explains the properties of LHe-4 at quantitative scale is still awaited. Guided by this observation we worked out a new approach to develop our non-conventional microscopic theory (NCMT) of a SIB by solving the N particle differential Schrodinger equation. We note that different approaches (viz., variational quantum approach and second quantization clubbed with perturbation techniques) to conventional microscopic theory (CMT) of a SIB use single particle basis (SPB) in a sense that each particle is presumed to represent a single particle kept in a box of volume V of the system with its states described by plane waves; in other words a single particle represents the basic unit of the system. However, for the reasons which become clear in the process of the formulation of our theory, we use pair of particles basis (PPB) which identifies a pair of particles as the basic unit of the system.The paper is arranged as follows. The Hamiltonian of a SIB like LHe-4 and the wave mechanics of a pair of particles are critically analyzed to lay down the basic foundations of our approach in Section 2. While the wave function of N−particle states (with corresponding eigen energies) and ground state (G-state) configuration are determined in Section 3, a detailed analysis of the λ−transition and related aspects is studied in Section 4. The origin of bound pair formation and energy gap (a kind of collective binding among all the N particles) between superfluid (S) and normal fluid (N) phases of the system and its relationship with superfluidity and related aspects are revealed in Section 5. Important aspects of Bogoliubov’s picture, two fluid theory, Ψ−theory, etc. and crucial experimental observations which render decisive support to our theory are briefly analyzed in Section 6. While important aspects of our theory and CMT are summarized in Section 7 for their comparison, useful concluding remarks are made in Section 8.
2. Basic aspects of a SIB
2.1. Hamiltonian
- An N particle SIB like LHe-4 is described[9], to a good approximation, by
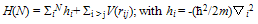 | (1) |
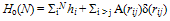 | (2) |
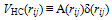 | (3) |
2.2. Dynamics of a Pair of Particles
- Although, particles in a SIB like LHe-4 under certain physical conditions can be treated, to a good approximation, as independent particles, even CMTs based on SPB consider particles in pairs to evaluate their potential energy since they interact through two body interactions, V(rij). This shows that consideration of single particle as a basic unit of the system does not have general validity. Evidently, for a complete and better understanding of a SIB we need to consider a pair of particles as its basic unit whose dynamics can be described in the CM coordinate system by
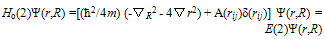 | (4) |
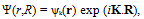 | (5) |
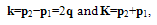 | (6) |
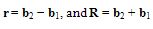 | (7) |
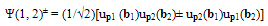 | (8) |
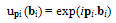 | (9) |
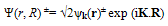 | (10) |
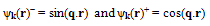 | (11) |
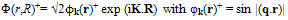 | (12) |
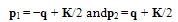 | (13) |
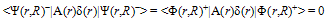 | (14) |
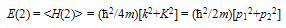 | (15) |
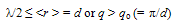 | (16) |
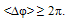 | (17) |
2.3. Macro-orbital Representation of A Particle
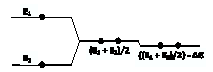
- As evident from Eqn.15, the wave superposition of P1 and P2 leading to Ψ(r,R)− (Eqn.10) or Φ(r,R)+ (Eqn.12) does not alter their net energy E(2) = ћ2p12/2m + ћ2p22/2min their states represented by two plane waves. This implies that: (i) P1 and P2 in Ψ(r,R)− /Φ(r,R)+ states behave, energetically, like independent particles, (ii) E(2) is shared equally among P1 and P2 and (iii) the superposition brings P1 and P2 (having different energies, E1 = ћ2p12/2m and E2 = ћ2p22/2m) to a single energy state of (E1+E2)/2 (cf., Fig.1). Evidently, each of the two fermions/bosons, in Ψ(r,R)− /Φ(r, R)+ state, can be identified as an independent particle in a state represented by
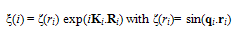 | (18) |
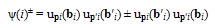 | (19) |
3. N-particle State
3.1. State Function
- Using N macro-orbitals for N particles, we obtain
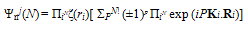 | (20) |
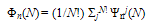 | (21) |
3.2. State Energy
- We define
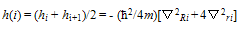 | (22) |
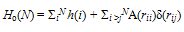 | (23) |
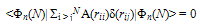 | (24) |
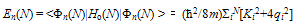 | (25) |
3.3. Ground State
- With a view to determine the G-state energy of our system, we first use our inference that q ≥ qo (Eqn.16) and the fact that K can have any value between 0 and ∞ to find
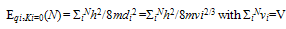 | (26) |
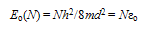 | (27) |
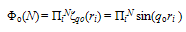 | (28) |
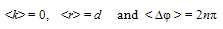 | (29) |
4. λ−Transition and Related Aspects
4.1. Equation of State
- In what follows from Section 3 and Eqn.(15), energy (ϵ) of a single particle can be written as
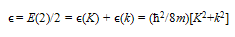 | (30) |
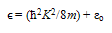 | (31) |
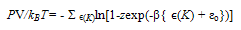 | (32) |
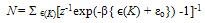 | (33) |
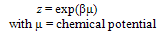 | (34) |
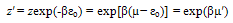 | (35) |
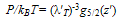 | (36) |
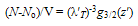 | (37) |
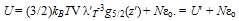 | (38) |
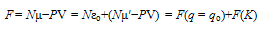 | (39) |
4.2. Onset of K = 0 Condensate and Tλ
- In what follows from Eqns.36 and 37, we can apply the standard theory of a SNIB[9] to conclude that a SIB should exhibit a transition at
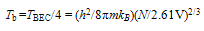 | (40) |
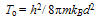 | (41) |
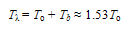 | (42) |
4.3. Nature of Transition
- Following Section 3.3, we find that the system transforms from a state of random distribution of its particles in φ−space to that of orderly distribution with φ = 2nπ (n = 1, 2, 3, ..), when it is cooled through Tλ. Evidently, the λ−transition is an onset of order-disorder of particles in φ−space followed by the BEC of particles in the state of K = 0 and q = π/d. We note that the BEC of particles in K = 0 state is not different from the BEC of non-interacting bosons (a well known second order transition[9]) and the order-disorder of particles in φ−space is accomplished simply by a reshuffle of their momenta (kinetic energy) without any change in inter-particle distance and potential energy; this means that there is no change in the total energy of the system at λ−point which concludes it to be second order transition.
4.4. Free Energy and Order Parameter of Tλ
- Following Section 4.1, we have
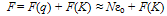 | (43) |
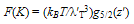 | (44) |
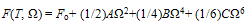 | (45) |
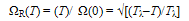 | (46) |
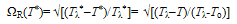 | (47) |
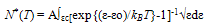 | (48) |
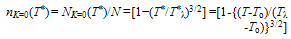 | (49) |
4.5. Single Particle Density Matrix and ODLRO
- The single particle density matrix ρ1(R′−R), -a measure of the probability of spontaneous motion of a particle from R to R′ or vice versa assumes significance at T ≤ Tλ. ρ1(R′−R) is also known as the measure of off diagonal long range order (ODLRO). To obtain ρ1(R′−R) for our system, we note that: (i) to a good approximation, almost all particles in a SIB[in its LT phase as well as at Tλ+ (just above Tλ) in HT phase] have (q, -q) pair state with q = qo and (ii) such a particle, when made to move with momentum ∆q, assumes a state of (q+∆q, -q+∆q) which not only implies that its state changes from
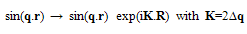 | (50) |
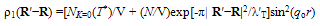 | (51) |
4.6. Evolution of the System on Cooling
- The q−motion state of a particle in the system can be characterized by a parameter s = d − λ/2 which decreases with cooling of the system since λT/2 = h/2√(2πmkBT) (thermal average of λ/2) increases and d remains constant (or nearly constant). Evidently, since s is restricted to have only +ve value in the light of the condition λ/2 ≤ d (Eqn.16), the number of particles occupying a state of s = 0 (i.e., λ = 2d or q=qo= π/d) keep on increasing with falling T till the system reaches a point where it satisfies λT/2 = d (a condition which means that all particles, on an average, occupy the state of s = 0). As soon as, this happens, particles cease to have a possibility of any increase in λ/2 because it demands increase in d which is decided independently by V(rij). Evidently, λ/2 of particles at this point gets locked at d or equivalent q at qo = π/d indicating that q−motions of particles are left with no energy to lose. Naturally, this forces particles to lose their K−motion energy for which the system sees an onset of their condensation in a state of q = qo and K=0 at Tλ given by Eqn.(42). Naturally, the state of s = 0 (or of q = qo) is occupied by almost all particles at Tλ; the state of the system at T<Tλ differs only in the energy of K−motions which now corresponds to collective excitations of the system such as phonons and rotons. Consequently, using q = qo for all particles in Eqn.21, the state of a SIB at T ≤ Tλ can be expressed by
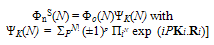 | (52) |
4.7. Volume Expansion on Cooling
- In what follows from Sections 4.1, 4.2 and 4.6, the q−motion energy of almost all particles gets frozen at q= qo with corresponding energy εo(Tλ) = h2/8md2 when a SIB is cooled to T = Tλ. However, if the system is cooled below Tλ, its each particle tries to, naturally, have an energy < εo(Tλ) which, obviously, corresponds to λ/2 > dλ which does not agree with the restriction λ/2 < d (Eqn.16). Evidently, any fall in q−motion energy below εo(Tλ) needs an increase in d beyond dλ (decided by a balance of forces representing V R(rij) and VA(rij)); however, this is made possible by the zero-point repulsive force, fo = −∂dεo = h2/4md3, exerted by each particle on its neighbors against the inter-particle attraction, fa (originating from VA(rij)). It is clear that fo comes into operation effectively only around Tλ. We study the equilibrium of fo and fa in our recent study[60] of a quantum particle trapped in a 1-D box and Section 5.1(ii) for the present case. It is evident that the said equilibrium leaves an increase in the cavity size by ∆d = dT − dλ for almost all particles at Tλ. Consequently, the system on its cooling has to have a volume expansion around Tλ rendering εo of each particle to decrease by
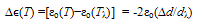 | (53) |
4.8. Quantum Correlations and Their Importance
- Here we show that quantum correlations between particles, originating from their wave nature, play an important role in relation to the behavior of a SIB. These can be expressed in terms of what is known as quantum correlation potential (QCP)[61-63] obtained by comparing the partition function (under the quantum limits of the system), Zq = Σnexp(−En/kBT )|ΦnS(N)|2 and its classical equivalent, Zc = Σnexp(−En/kBT)exp(−Un/kBT). Here ΦnS(N) is given by Eqn.52; note that the system at any given instant, even at T > Tλ, exists in one of the N! micro-states Ψnj(N) (Eqn.20) which hardly differs from ΦnS(N) particularly at Tλ. The application of this method to our system is justified because our theory describes its particles by summarized plane waves rendering
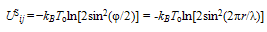 | (54) |
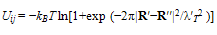 | (55) |
5. Superfluidity and Related Aspects
5.1. Energy Gap and Bound (q,-q) Pairs
- Following Sections 4.1 and 4.4, we note that: (i) cooling a SIB through Tλ decreases F(K) (Eqn.44) to its zero value at T = 0 and keeps F(q) (Eqn.43) at F(qo) = Nεo which remains nearly constant for a change in T from Tλ → T = 0, and (ii) ρs (representing the order parameter, Ω, Section 4.4, Fig.2) has maximum value at T = 0 where K−motions cease to exist. Evidently, the most relevant part of the free energy which is responsible for the superfluidity and related properties of LT phase of a SIB is F(q), -not F(K). This is corroborated by the fact that ρs decreases with increasing T indicating that increase in the amount of thermal excitations (or their representative F(K)) has a counter effect on these properties.In what follows from Section 4.7, each particle in a SIB exerts zero point force fo which not only tries to keep two particles at a distance of λ/2 (the size of their WPs) which increases with decreasing T but also forces an increase in d against the inter-particle attraction fa. Since fo comes into force before such a SIB reaches its T of solidification, VA(rij) fails to transform the fluid into solid as its normal goal. However, VA(rij) limits the inevitable increase in d (or equivalent increase in V) to a smallest possible value ∆d = dT − dλ. Evidently such a SIB is expected to have its volume expansion around Tλ by an amount permitted by a balance between fo and fa . The fact that this expectation agrees with experimentally observed volume expansion of LHe-4 on its cooling through Tλ[2(a)] not only reveals that the onset of λ−transition also has its relation with the interplay of fo and fa but also provides experimental support to the WP manifestation of particles in the fluid at T = 0 → Tλ+ (a T little above Tλ ); this is not surprising since the WP manifestation of a particle is one of the basic foundations of wave mechanics. Interestingly, as concluded from the following discussion, the balance of fo and fa also renders a kind of collective binding Eg(T ) (or an energy gap between S-state such as He-II and N-state such as He-I) (see Eqn.60, below) among all the N particles below λ−point. Qualitatively, this kind of binding is also concluded[cf., point (i) below] by following a standard method used to understand molecular binding[64] where two identical atomic orbitals form two molecular orbitals of bonding and anti-bonding nature.(i). VA(rij) as source of collective binding: To understand how VA(rij) produces binding of two particles like 4He atoms in the state of their wave superposition, we diagonalize (2x2) energy matrix, defined by E11 = E22 = εo and E12 = E21 = βo, with βo = <VA(rij)>; to this effect we note that two such particles have identically equal energy εo (cf., Fig.1(middle)). The diagonolization renders two states of energy εo ± |βo| for the pair; one may better replace |βo| by |βo(T)| since the overlap of macro-orbitals of two particles may depend on T. The states of energy (εo − |βo(T)|) and (εo + |βo(T)|) can, respectively, be identified as bonding (or paired) and anti-bonding (or unpaired) states. The pair is expected to be in bonding state (cf., Fig.1(right)) provided the two particles remain locked in the relative configuration characterized by Eqn.29. The fact, that this situation arises for almost all particles (excluding a small fraction of particles in states of q ≥ 2qo) only at T ≤ Tλ, distinguishes the state of particles in the LT phase (such as He-II) from that in HT phase (He-I). In the following discussion we use bonding states of particles to conclude what we call as an energy gap Eg(T) (cf. Eqn.60, below) or their collective binding.Applying the same approach to the state of all the N particles, we construct a NxN matrix for Hr(N) = −(ћ2/m)Σi▽i2 + Σi
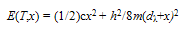 | (56) |
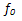 . Using
. Using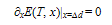 | (57) |
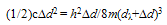 | (58) |
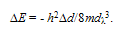 | (59) |
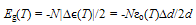 | (60) |
5.2. Energy Gap and its Consequences
- In what follows from Section-4.4, a SIB has two components, fluid F1 and fluid F2 with free energies represented, respectively, by F(K) and F(q). F(K) and F(q) get delinked from each other at Tλ with freezing of q−motion at q = qo (cf. Section 4.8). Hence the fact, that F(K) represents quasi-particle excitations originating from K−motions (unaffected by interactions), implies that only F(q) is affected by Eg(T) and we have F(q) = Nεo(Tλ) − Eg(T) which, obviously, means that the origin of different LT properties (including superfluidity and related aspects) of a SIB lies with Eg(T). We use this inference to analyze the following aspects of a SIB at T ≤ Tλ.
5.2.1. Superfluidity and Related Properties
- If two heads X and Y in the system have small T and P (pressure) differences, the equation of state can be expressed as Eg(X) = Eg(Y ) + S∆T − V∆P . Using Eg(X) = Eg(Y ) for equilibrium, we get
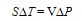 | (61) |
5.2.2. Critical Velocities and Stability of LT phase
- Following Eqn.50 and the basic arguments behind it, we find that the G-state wave function Φo(N) changes to
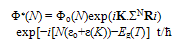 | (62) |
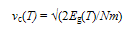 | (63) |
5.2.3. Coherence length
- Since the main factor responsible for the coherence of F2 is its configuration which locks the particles at ∆φ = 2nπ (cf. Eqn.29) with collective binding Eg(T), the coherence length (not to be confused with healing length[5]) can be obtained from
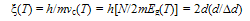 | (64) |
5.2.4. Superfluid Density
- Correlating the superfluid density, ρs, as the order parameter of the transition, with Eg(T), we find
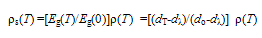 | (65) |
5.2.5. Superfluid Velocity
- Concentrating only on the time independent part of Φo*(N) (Eqn.62), we can have
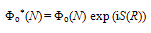 | (66) |
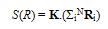 | (67) |
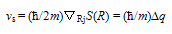 | (68) |
5.2.6. Quantized Vortices
- Using the symmetry property of a state of bosonic system, Feynman[15, 69] showed that κ (the circulation of the velocity field) should be quantized and be given by κ = n(h/m) with n = 1, 2, 3, ... However, Wilks[2(a)] has rightly pointed out that this account does not explain the fact that He-I to which Feynman’s argument applies equally well, does not exhibit quantized vortices. Using Eqn.67, we find that
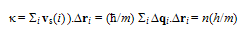 | (69) |
5.3. Laser Like State
- We note that the system below Tλ defines a 3-D network of SMWs, extending from its one end to another end without any discontinuity. In lasers too these are the standing waves of electromagnetic field that modulate the probability of finding a photon at a chosen phase point. The basic difference between the two lies in the number of bosons in a single anti-nodal region of a SMW. In case of lasers this could be any number since photons are non-interacting particles but for a SIB like 4He or 87Rb one such region can have only one atom.
6. Facts which Corroborate Our Theory
6.1. Thermodynamic and Hydrodynamic Properties
- We note that the excitation spectrum of a SIB (E(Q) = ћ2Q2/4mS(Q), with S(Q) being the structure factor of the fluid at wave vector Q), as concluded by our theory[70], not only agrees well with Landau spectrum[6(b)] at qualitative level but also matches closely with the experimentally observed spectrum[4, 25, 31] for LHe-4 at quantitative level. Similarly, the calculated values of vc, ρs and ρn, etc., by using relevant relations (Section 5.2), are found to agree[71] closely with their experimental values for LHe-4[5]. In what follows these facts ensure that our theory has great potential to accurately account for the thermodynamic and hydrodynamic properties (including superfluidity and related aspects) of the S-phase of a SIB.
6.2. Phenomenological Pictures
6.2.1. Two Fluid Theory
- As concluded from Sections 4.4 and 5.2, a SIB at T ≤ Tλ gets separated into two fluids F1 and F2. While, F2 has all characteristic properties of a superfluid viz., zero entropy, zero viscosity, etc., since it comprises particles in their G-state with their positions locked at <k>= 0, <r>= λ/2 = d and ∆φ = 2nπ (Eqn.29) for which they cease to have relative motion (or collisional motion), F1 identified with a gas of non-interacting quasi-particle excitations, has all properties (such as non-zero entropy, non-zero viscosity, etc.) of a N-fluid. This not only concludes that a SIB below Tλ should, undoubtedly, behave as a homogeneous mixture of two fluids that have all properties envisaged by Landau[6] but also provides microscopic foundation for two fluid phenomenology. It further reveals that each particle with its q−motion participates in F2 and with K−motion in F1. It does not support the perception that certain atoms participate in F1 and rest in F2.As an important aspect of Landau’s two fluid theory, S-fluid component of He-II is assumed to flow in a direction opposite to N-fluid component which flows from the point of higher T to that of lower T. Our theory finds a sound reason for it. Since ρs(T) and VS(T) = NϵS(T) both have monotonic increase with decrease in T, a point of lower T has higher amount of both, ρs(T) and VS(T), in comparison with a point of higher T. Naturally, particles having higher value of VS(T) at a region of lower T experience a force which make them move towards the region of higher T where they have lower VS(T) unless the two regions attain a state of equal VS(T), i.e. a state of equal strain energy which happens to occur at points of equal T. Alternatively, this means that ρs(T) flows from the region of lower T towards the region of higher T unless the two regions have equal ρs(T). Note that liquids cannot sustain pockets of different strain energy, NϵS(T), obviously, for its fluidity which allows them to flow from the regions of higher strain energy to those of lower strain energy and this task is completed by flow of omons which have higher density in the regions of lower T in comparison to those of higher T.
6.2.2. Ψ−theory
- We find that superfluidity of a SIB is basically a property of its F2 component (or the G-state) represented by Φo(N) (Eqn.28) which can also be expressed as
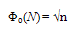 | (70) |
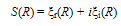 | (71) |
6.2.3. Quantum Phase Transition
- As discussed in Section 4.8, our theory finds that λ−transition and superfluidity are the results of quantum nature of particles. When this observation is clubbed with the fact that superfluidity is basically a property of F2 component (comprising particles in their T = 0 state) of a SIB. However, F2 exists even at non-zero T < Tλ due to its proximity with F1 (a gas of quasi-particle excitations) whose energy measures the T of the system. In what follows λ−transition could be identified as a quantum transition[72] which occurs at non-zero T for the said proximity. Although, particles in excited states attributed to their q−motions (viz., with q = 2qo , 3qo, ...,etc.) are, naturally, the part of F2, however, their number are found to be only ≈ 5% at Tλ and it decreases exponentially to 0 value at T = 0.
6.3. Other Experimental Observations
- (i). Physical reality of existence of an electron bubble: An excess electron in liquid helium exclusively occupies a self created spherical cavity (known as electron bubble) of certain radius, when it assumes its lowest possible energy in the cavity. To create the said cavity it exerts its zero-point force on the surrounding atoms against the forces originating from inter-atomic interactions and external pressure on the liquid[73]. It is evident that the bubble formation is a consequence of the facts that: (i) an excess electron experiences a strong short range repulsion with He atoms which does not allow its binding with the said atoms and (ii) the electron, for its quantum nature, manifests as a WP whose size increases with the decrease in its energy. This implies that any quantum particle that experiences similar repulsion with He atoms should have similar state in liquid helium and this is found to be true with positron[74] and other particles (ions, atoms, molecules, etc.[75]). Guided by these observations, it is natural to believe that each 4He-atom in LHe-4 should assume similar state when it occupies its lowest possible energy because it too is a quantum particle and it experiences strong short range repulsion with other helium atoms. Here we also find that the electron in a drifting bubble has two motions (q− and K−motions), respectively, identified with its zero-point motion as a trapped particle and its drift with the bubble. This not only helps in having a better understanding of the two motions of a single quantum particle in a SIB like LHe-4, but also proves that the state of the electron in electron bubble is not different from the state that we represent by a macro-orbital. In other words the existence of an electron bubble not only renders a clear experimental proof for the macro-orbital state of a HC boson in a SIB like LHe-4 and provides strong experimental foundation to our theory but also reveals that ζ(r) part of the macro-orbital (Eqn.(18)) for s−, p−, d− .... states can be represented to a good approximation by the respective state functions of a particle trapped in a spherical cavity of size d[76].(ii) Spectroscopy of molecules embedded in He-droplets or clusters: Experimental study of high resolution rovibrational spectra of embedded molecules (e.g., OCS/N2O molecule in 4He droplets and 4Hey:OCS or 4Hey:N2O clusters[77] where y = number of 4He atoms) provides another foundation to our theory because these studies conclude that superfluidity exists even in systems having few 4He atoms (viz., about 6 or more) which implies that the phenomenon has no relation with p = 0 condensate since 4He atoms in these systems are confined to a space of size, s ≈ 5Ǻ for which each atom is expected to have reasonably high momentum ≈ π/s rather than zero. Further since each cluster is expected to have certain stable structure (which of course would depend on inter-particle interactions and may change with change in y), the embedded molecule sees a time independent potential which implies that 4He atoms around the rotor cease to have collisional motions. In other words 4He atoms in these droplets and clusters are localized with position uncertainty decided by their least possible momentum of their confinement which agrees closely with our theory. In addition, as inferred in Section 3.3, particles in S-state of a SIB can move with equal velocity on a closed path without any change in order of their locations which implies that particles on two such nearest possible paths (viz., two concentric circular paths) can have different velocities consistent with the theory of experimentally observed quantized circulation in superfluid 4He[5]. Evidently, it is not surprising that a molecule (or its cluster with few neighboring atoms which bind with it to follow its rotation) is observed to have free rotation within a 3-D shell or a ring (formed by 4He atoms in its surrounding) that does not participate in the rotation. It also finds that OCS or N2O molecule embedded in S-state of 4He droplets shows sharp rotational lines because 4He atoms cease to have collisional motion but not in N-state of 3He[77(a)] where particles are known to have mutual collisions. In other words rotational lines do not have collisional broadening in superfluid 4He which they have in liquid 3He. As such experimental observations related to the rovibrational spectra of embedded molecules support our theory.
6.4. Experimental Evidence for CPA-WP
- Diffraction experiments using X-ray, neutron and electron beams are expected to provide accurate information about the atomic arrangement in any system provided the high energy/momentum of these radiations does not damage/perturb this arrangement. Although, atoms in CPA-WP cease to have their relative motions, they remain the parts and parcel of a fluid where shear forces have vanishingly small magnitude which makes CPA-WP highly fragile. It differs significantly from the atomic arrangement in a solid/crystal which have appreciably strong shear forces. Particles in CPA-WP remain free to move coherently (all with same velocity keeping their relative positions, residual momentum and the relative phase positions fixed) in order of their locations on a line/closed path (or bundles of parallel lines/closed paths). In other words, atoms in He-II can slip on a line/plane with respect to those on neighboring lines/planes; they are likely to get displaced from their positions with a collective motion when they are hit by particles of high energy/momentum in a beam of said radiations. Even the relative distance of particles is expected to change, since it depends on the size of their WPs (λ/2 = π/q) which can have large fluctuations when the system is exposed to the said radiations. Evidently, the said diffraction tools are not suitable to get reliable information about the CPA-WP and it is for this reason that CPA-WP could not be detected for so long.However, we identify other experiments which prove CPA-WP of 4He-atoms in He-II from the fact that this arrangement locks atoms at a distance d, relative momentumat k = 2qo = 2π/d and relative phase position ∆φ = 2nπ. To this effect we note the following:(1).The excitation spectrum E(Q) of He-II matches closely with that predicted for a mono-atomic chain with atoms separated by d not only at low Q (observed for most liquids) but also at high Q(> 2π/d). The momentum and energy of an excitation at such a high Q basically correspond to a motion of a single particle for the fact that the corresponding wave length Λ < d (the size of space occupied by a particle); this clearly proves that particles have an orderly arrangement with a separation d.(2) Landau two fluid model which explains the properties of He-II to a good accuracy envisages S-component of He-II to have S = 0 and η = 0 and CPA-WP representing this component has S = 0 because all particles occupy single quantum state of q = qo and η = 0 because particles cease to have relative motions or mutual collisions for their relative positions remain locked with r = d.(3) Superfluid is observed to have coherent motion and vortices of quantum circulation and their possibility demands a configuration like CPA-WP where particles satisfy ∆φ = 2nπ. Although, the above listed experimental observations have been there for many years, however, these were not analyzed to see the existence of CPA-WP because it was not perceived in the framework of CMT. Finally, we also note that several other experimental observations on He-II, such as T3 dependence of specific heat, infinitely high thermal conductivity, etc. too support CPA-WP.
7. Comparison of our NCMT and CMT
7.1. Important Aspects of our NCMT
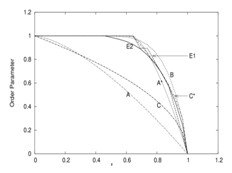
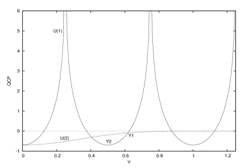
- Our approach to the microscopic understanding of a SIB uses PPB which identifies each particle as a representative or a part of a pair of particles moving with equal and opposite momenta (q, -q) with respect to their CM which moves with momentum K. Consequently, the state of the particle is represented by a macro-orbital (Eqn.18) and the accuracy of this representation is established, beyond doubt, by the existence of electron bubble[Section 6.3(i)]. It is further strengthened by the fact that this representation identifies each particle to have two motions (q− and K−) which provide the origin of two fluid behavior of He-II (Section 6.2(ii)).The onset of λ−transition is an order-disorder of particles in φ−space followed, simultaneously, by their BEC in the state of q = qo and K = 0. The T dependence of the condensate fraction nK=0(T∗) (Eqn. 49) starting from nK=0(Tλ) = 0 to nK=0(T∗ =0) = 1.0 agrees closely with experimentally observed ρs(T)/ρ for He-II which represents a kind of order parameter of the transition (Curves A∗ and E2, cf. Fig. 2).The fact that λ−transition is a consequence of the wave nature of particles is made more clearly visible by our theory, since it finds: (i) how wave nature of particles leads to their quantum correlations represented by corresponding potentials (USij (Eqn.54) and Uij (Eqn.55) depicted in Fig. 3) which drive their q and K, respectively, toward q = qo and K = 0, (ii) how zero-point force (another consequence of the wave nature), fo = h2/4md3, exerted by each particle on its neighbors pushes them away against the inter-particle attraction, fa (originating from inter-particle potential) and renders an increase in d by dT−dλ (Section 4.7) representing a kind of mechanical strain in inter-particle bonds when fo and fa reach a state of equilibrium, (iii) why energy of this strain, ∆VS(T) = NϵS(T) (Section 5.1), depends on the q−values (fluctuating around qo) of particles for which the system sustains a new quantum quasi-particle omon similar to a phonon (Section 5.1), (iv) how zero-point energy (yet another consequence of wave nature) of each particle falls by small amount (Eqn.53) and how Eg(T) (Eqn. 60) represents a collective binding between all atoms for which the entire system behaves like a macroscopic single molecule, (v) how collective binding serves as an energy gap Eg(T) between S-state and N-state (Section 5.1), (vi) how this gap helps in accounting for the superfluidity and related properties of He-II (Section 5.2), and (vii) how zero-point force (Section 4.7) serves as a basis for our prediction that a SIB should exhibit −ve thermal expansion coefficient around Tλ which is confirmed by the experimental observation on LHe-4[2(a)].The theory reveals that the S-state is characterized by a fraction of particles[nK=0(T∗)] condensed into the G-state represented by q = qo and K = 0 with no particle having q < qo . It not only concludes the absence of p = 0 condensate but also explains why existence of p = 0 condensate in He-II could not be confirmed through any experiment beyond a point of doubt[26-28]. Inferences of our theory are also consistent with the criteria of the occurrence of BEC, viz. (i) the expected observation of ODLRO[55, 56], (ii) spontaneous symmetry breaking[57] and phase coherence[58], as well as with the excluded volume condition envisaged by Kleban[78] who argued that each 4He-atom in LHe-4 occupies certain volume exclusively.The theory also explains why LT phase of a SIB should behave like a homogeneous mixture of two fluids[(F1 (normal) and F2 (super) found to have different properties[7] as envisaged exactly by Landau’s theory[6]] and thereby renders microscopic basis to two fluid theory and Ψ−theory[37]. It further reveals that Superfluidity and related properties are, basically, associated with the T = 0 state of the system (represented by F2) which means that λ−transition is a kind of quantum transition which occurs at a non-zero T for the proximity of F2 with F1.Particles in F2 represent (q, -q) bound pairs, not only in q−space but also in r−and φ−spaces. They constitute a kind of CPA-WP and define a 3-D network of SMWs which locks their relative momentum, relative separation and relative position on φ−line, respectively, at k = 2π/d, r = d and ∆φ = 2nπ with a net amount of collective binding represented by Eg(T); this provides reasons for the stability of S-state for small energy perturbations such as its flow (linear/rotational) with a velocity below certain values or small amplitude thermal oscillations. The S-state is consistent with microscopic uncertainty as evident from q ≥ π/d as well as macroscopic uncertainty since the 3-D network of SMWs represented by ΦSo(N) (Eqn.28) vanishes at the boundaries of the system.Our theory predicts that a SIB can have an onset of superfluidity provided it keeps its fluidity up to a T ≈ To ≡ εo) at which the zero-point force of its particles dominates its physical state. Since the WP size (λ/2) for all particles in the S-state of a SIB remains as small as d (Eqn.(42)), it is not surprising that superfluidity is observed in nano droplets and clusters of few atoms as reported recently in[75, 77].The merit of our approach lies with the fact that it concludes the present theory simply by analyzing the solutions of its N−particle Schrodinger equation. It makes no assumption such as the existence of p = 0 condensate or pair condensate, etc. in the S-phase of a SIB as made by CMT. The theory is mathematically simple and its results cannot be manipulated since it uses no adjustable parameter. It does not use any drastic approximation in determining the role of inter-particle interactions. It beautifully demonstrates that the wave nature has amazing capacity to organize particles in phase space at φ = 2nπ with <r>= λ/2 = d.
7.2. Important Aspects of CMT
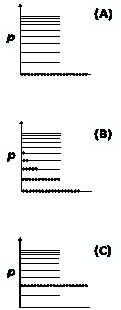
- Following the basic theory of BEC[9] in SNIB, one finds that 100% particles occupy a single particle state of p = 0 (presumed to represent the G-state of the system) as depicted by Fig.4(A). However, as indicated by Bogoliubov’s theory[8], this does not hold for a SIB; Np=0 gets depleted by Np≠0 = N − Np=0 which move to different states of p ≠ 0 beca use the G-state energy of the system increases by certain value (say, ∆Eo) due to inter-particle repulsion V R(rij); the momentum distribution of particles (N(p)) in the G-state of a SIB, so expected is shown in Fig.4(B). Np≠0 and ∆Eo, presumably, increase with the increasing strength of V R(rij). CMT calculations reveal that p = 0 condensate gets depleted to a value as low as ≈ 10%[25-28] in He-II and ≈ 60% or more in TDG[40]. However, recent theoretical studies of He-II and TDG consider that S-phase of a SIB also has intensive pair coherent condensate (PCC), -analogous to the Cooper condensate in a Fermi liquid with an attraction between the fermions. Having a slightly different view point Jeon et al[47(a)] and Hao[47(b)] try to revive an old consideration[48(a-c)] and try to conclude that the unique properties of the S-phase of a SIB are the consequences of the condensation of only Cooper type pairs of 4He-atoms. Interestingly, since N(p) in the G-state of a SIB, as concluded by all these theories, does not differ qualitatively from that depicted in Fig.4(B), it is clear that these theories differ only for their presumed emphasis on single particle condensate or pair condensate or composite condensate as the origin of superfluidity and related aspects. However, in the absence of a clear experimental evidence in support of the existence of any form of the condensate, this difference may have only academic importance; what remains to be noted is that all these studies use SPB to describe a SIB and approximation methods (perturbative or variational) to reach their conclusions and in this context it is important to note that single particle representation does not agree with a physical reality of the LT states of a SIB in which particles bound to have states of their wave superposition which cannot be understood unless we take at least two waves as discussed in Section 2.2.
7.3. Should Results of PPB and SPB Approaches Differ?
- “Physical quantities should not depend on the basis (SPB or PPB) used for describing a system, if the theoretical treatment is exact. This motivated us to examine the reason for the difference of G-state of a SIB concluded by SPB (Fig.4(B)) and that concluded by PPB (Fig.4(C)) because no system can be correctly understood unless we have the correct understanding of its G-state. In this context our simple mathematical analysis[79], unequivocally, concludes that N(p) (Fig.4(B)) does not represent a state of minimum possible energy as expected for every physical system in its G-state. Subjecting N(p) (Fig.4(B)) to the condition which can minimize its energy, we discovered[79] that: (i) all particles in the true G-state of a SIB should have identically equal energy εo = h2/8md2 and equivalent momentum q = qo = π/d, and (ii) no particle has a q < qo which establishes the absence of p = 0 condensate. In the light of the fact that these inferences agree exactly with corresponding ones of our theory and our results (for the G-state) of a SIB can be obtained from those of CMT (not vice versa) simply by minimizing the energy of N(p) (Fig.4(B)), we can use the opening statement of this section to state that our theory is nearly exact.A quantum theory is said to be exact if it finds solutions of the Schrodinger equation of a system without leaving any part of the potential involved. To this effect it may be noted that our theory starts by using V(rij) = VR(rij) + VA(rij) without any approximation. In a next step it uses an approximation VR(rij) ≡ VHC(rij) ≡ A(rij)δ(rij) and replace the contribution of VA(rij) by −Vo in a good agreement with the physical realities of a fluid (i.e., particles in a fluid move freely like impenetrable hard balls; two particles encounter infinitely strong potential only when their bodies have a mutual touch). Finally, when the system is dominated by the wave nature of particles at LTs with their wave superposition, our theory considers their zero-point repulsion (a combine of A(r)δ(r) and WP manifestation of a particle) in its totality and derives its consequences by balancing fo and fa (Section 5.1) and in this process it uses only one approximation in which fa is derived from a harmonic potential, (c/2)x2, while its source potential VA(rij) can contribute an-harmonic terms too. Evidently, all these points justify that our theory is nearly exact.
8. Conclusions
- This paper reports a nearly exact microscopic theory of a SIB by solving N−body Schrodinger differential equation by using the simplest possible method. The accuracy of our theory finds strong experimental support from: (i) the agreement of its concluded excitation spectrum, E(Q) = ћ2Q2/4mS(Q)[65,70], (planned to be published as Paper-II) with experimentally observed E(Q) of LHe-4[25], (ii) conformity of its calculated values of the parameters of two fluid hydrodynamics(viz., ρs(T), ρn(T), etc. reported in[71]) with corresponding experimental results for He-II[5], (iii) experimentally observed quantized circulation, (iv) flow of ρs(T) in the direction opposite to that of ρn(T) which flows from the region of higher T to that of lower T, etc.Its concluded energy gap (Eg(T)) between the S-state and N-state of LHe-4 not only serves as the origin of superfluidity and related aspects but also provides reasons for the stability of the S-state against the small energy perturbations. This is demonstrated by the fact that the critical velocity of its linear flow (vc) and that of its rotational flow (Ωc) (for which its superfluidity is totally lost) obtained by us[71] from Eg(T) for He-II agree closely with experiments[5]. Since the maximum value of per particle share in Eg(T) (Eqn.(60)) for He-II falls around mK energy, superfluidity is an energetically weak effect and this is evident from the small values of vc and Ωc. As concluded in Section 4.4, BEC of bosons (in a SNIB as well as a SIB like LHe-4) has a unified picture in the framework of our NCMT; for both cases it can be identified as a condensation of particles in their G-state where each particle has <p>= 0 (not p = 0). It may be noted that: (i) momentum of a particle in both systems (SNIB and SIB) kept in finite V does not remain a good quantum number, particularly, when their λT becomes of the order of d and (ii) each particle even in the G-state of a SNIB has non-zero energy (≈ h2/8mV2/3) and corresponding non-zero momentum (q = qo ≈ π/V1/3). The fact that corresponding energy and momentum values for a SIB fall at about N2/3 and N1/3 times higher speaks of the impact of the HC interaction among the particles in a SIB; N = 1000, these factors, respectively fall at 100 and 10, while for N = 1024, they fall at 1016 and 108 which are very large factor. To this effect we note that a particle in a SNIB has no means to know about the presence of other particles hence each particle behaves as if the entire V belongs to it. However, this is not the case for a SIB, since effective volume available for each particle is only V/N.In what follows from ρs(Tλ) = 0, it can be stated that the onset of BEC at T= Tλ occurs merely few particles occupying the state of q = qo and K = 0 and ends with all particles having this state at T=0. Evidently, the
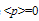 condensation in a SIB grows from
condensation in a SIB grows from 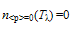 to reach
to reach 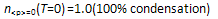 . Since this is consistent with ρs(Tλ) = 0 and ρs(0) = 1.0, our NCMT has no difficulty (of the type faced by CMT where only
. Since this is consistent with ρs(Tλ) = 0 and ρs(0) = 1.0, our NCMT has no difficulty (of the type faced by CMT where only 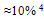 He atoms are found to have p = 0 even at T = 0) in using two fluid description of He-II.CMT based on SPB approach can also help in concluding the true G-state (Fig.4(C)) of a SIB provided the energy (corresponding to the G-state N(p) (Fig.4(B)) concluded by it) is minimized by making pairs of particles, -as shown in[79]. Evidently, the difference of CMT results with those of ours are the consequences of its SPB approach clubbed different possible presumptions and approximations, -not of the mathematical approach(es) used in it. We applied our approach to study some other MBQS. As, discussed briefly in[80], it has great potential to unify the physics of widely different systems of interacting bosons and fermions including low dimensional systems, newly discovered BEC states of TDG, etc. Our studies of N HC particles in 1-D box[81] and basic foundations of the microscopic theory of superconductivity[82] make it evident that a fermionic system differs from a bosonic system for its particle-distribution on the allowed states of K−motions which are constrained to follow Fermi-Dirac statistics in place of Bose-Einstein statistics followed for a bosonic system. Consequently, a fermionic system retains more energy in K−motions of particles even at T = 0. Consequently, fermions do not assume stable bound pairs unless their T falls below the T equivalent of Eg(T) where q−motions get delinked from K−motions; note that binding of particles controls only q−motions (relative motions) not the K−motions. This not only explains how excess energy of K−motions pushes down the T of the onset of superfluidity in a fermionic system in comparison to a bosonic system but also underlines the fact that superfluidity of both systems has a common origin which lies with the formation of bound SMW pairs. A SMW bound pair differs slightly from a Cooper pair for the basic source of its binding (Section 5.1(v)). Our approach finds that superfluid transition in a SIB should occur at a T ≈ To (≡ εo), while that in a fermionic system should occur around a T ≡ Eg(0)/N and this agrees closely with experimental values[36] of the temperature of the onset of superfluidity in LHe-4 and LHe-3, respectively.It is interesting to find that our theory of superconductivity[82] can account for the highest Tc of a high T superconductor that we know to-day. It can also explain the pressure dependence of the Tc of superfluid transition in LHe-3 at quantitative scale[83]. The zero-point force of a particle emphasized in these studies as the origin of a strain in the structure of the neighboring particles (viz. the lattice in case of superconductors and inter-atomic bonds in liquid 3He) is a natural consequence of wave nature of particles for which a particle behaves as a WP and occupies exclusively a space of size λ/2. This is clearly supported by the experimental observation that an electron in LHe-4 and LHe-3 exclusively occupies large size spherical cavity (or what is known as electron bubble) which has a radius of the order of ≈ 19Ǻ and the volume expansion exhibited by LHe-3 on its cooling below about 0.6 K[2(a)]. In a recent paper[84], we explained that only our theory concludes an ordered arrangement of particles (free from collisions) in the S-phase of a SIB desired to explain the experimental observation of Stark effect of roton transition[85] in He-II. Evidently, the observation of Stark effect renders strong experimental support to our theory and the absence of p = 0 condensate.Our non-conventional approach works well in developing the microscopic theory of a bosonic system like LHe-4 (as discussed in this paper) and a fermionic system like electron fluid in superconductors discussed in[82] (valid also for liquid 3He type systems). We hope that a critical discussion and scientific debate on our approach may further improve its strength and accuracy and it will help in concluding the desired theory of widely different many body systems of interacting bosons and fermions.It may be noted that our theory uses only the realistic picture of a fluid. It makes no assumption such as the existence of p = 0 condensate as the origin of superfluidity used by CMT. It is, obviously, consistent with the well known philosophical principle, -the Occam’s razor, which states that the explanation of a phenomenon should make as few assumptions as possible or the simplest solution of a problem is preferable to more complicated solutions. In this context it is interesting that our theory helps in clarifying the difference between S-fluid and N-fluid states even to a layman since these states can be identified, respectively, with: (i) the ordered positions and motions of soldiers in an organized army platoon and (ii) random positions and motions of people in a crowd. While the people in the former have coherent motion with no chance of mutual collision, those in the latter have incoherent motion with high probability of such collisions. The analogy seems to agree with what has been depicted in[86] about the BEC state of atoms in TDG and what has been perceived by Leggett[87] about 4He atoms in the so called p=0 condensate in He-II but with a difference. According to our theory, all atoms in the S-state of a SIB behave like soldiers in an organized army platoon, while in view of[86,87], this analogy applies only to the atoms which constitute the so called p = 0 condensate (i.e. about 10% 4He atoms in He-II or about 60% atoms in BEC state of TDG). In summary, we succeeded in developing the long awaited microscopic theory of a SIB like LHe-4 and TDGs. It finds that superfluidity of a SIB is basically a property of its G-state configuration which persists at all T < Tλ; it can be exhibited by a SIB of any size (as small as a microscopic cluster having a few bosons or as large as bulk LHe-4) provided the system retains fluidity at To(≡ εo). The theory predicts that such a SIB would exhibit –ve thermal expansion coefficient around its transition to superfluid state. It also predicts the presence of phonon like waves of oscillations in q values around qo (proposed to be known as omon) which propagate from the points (or regions) of lower T to those of higher T. For the first time our theory underlines the importance of the WP manifestation of a quantum particle and zero point force fo exerted by each of them on the neighboring particles in organising their relative positions in r- and φ-spaces. Our similar study of N interacting bosons confined to a 1-D box[81] clearly concludes that superfluidity and related properties can also be exhibited by systems of low dimensions (viz., 1-D and 2-D) below certain T(of the order of To). The results of our theory can have meeting points with those of CMT[8, 50] provided the energy corresponding to their concluded N(p) (Fig.4(B) is minimized. This point is concluded in our recent paper[79(c)] which not only reveals the absence of p=0 condensate but also demonstrates the possibility of N (=2, 3, ...) body correlations in superfluid state of a SIB; these correlations have been central to the recent developments in CMT[43-46]. The fact that our theory has been developed by solving its N-body Schrodinger equation in its standard differential form breaks the myth that such a solution is practically impossible to achieve. It also sets aside the speculation[5] that wave mechanics does not have basic principles to explain superfluidity of He-II. We hope that this theory would be accepted widely by the physics community and in this context, we would like to submit that 75 years is a long time to test the validity of the idea of p = 0 condensate as the origin of superfluidity. It is high time to give a chance to newer ideas.
He atoms are found to have p = 0 even at T = 0) in using two fluid description of He-II.CMT based on SPB approach can also help in concluding the true G-state (Fig.4(C)) of a SIB provided the energy (corresponding to the G-state N(p) (Fig.4(B)) concluded by it) is minimized by making pairs of particles, -as shown in[79]. Evidently, the difference of CMT results with those of ours are the consequences of its SPB approach clubbed different possible presumptions and approximations, -not of the mathematical approach(es) used in it. We applied our approach to study some other MBQS. As, discussed briefly in[80], it has great potential to unify the physics of widely different systems of interacting bosons and fermions including low dimensional systems, newly discovered BEC states of TDG, etc. Our studies of N HC particles in 1-D box[81] and basic foundations of the microscopic theory of superconductivity[82] make it evident that a fermionic system differs from a bosonic system for its particle-distribution on the allowed states of K−motions which are constrained to follow Fermi-Dirac statistics in place of Bose-Einstein statistics followed for a bosonic system. Consequently, a fermionic system retains more energy in K−motions of particles even at T = 0. Consequently, fermions do not assume stable bound pairs unless their T falls below the T equivalent of Eg(T) where q−motions get delinked from K−motions; note that binding of particles controls only q−motions (relative motions) not the K−motions. This not only explains how excess energy of K−motions pushes down the T of the onset of superfluidity in a fermionic system in comparison to a bosonic system but also underlines the fact that superfluidity of both systems has a common origin which lies with the formation of bound SMW pairs. A SMW bound pair differs slightly from a Cooper pair for the basic source of its binding (Section 5.1(v)). Our approach finds that superfluid transition in a SIB should occur at a T ≈ To (≡ εo), while that in a fermionic system should occur around a T ≡ Eg(0)/N and this agrees closely with experimental values[36] of the temperature of the onset of superfluidity in LHe-4 and LHe-3, respectively.It is interesting to find that our theory of superconductivity[82] can account for the highest Tc of a high T superconductor that we know to-day. It can also explain the pressure dependence of the Tc of superfluid transition in LHe-3 at quantitative scale[83]. The zero-point force of a particle emphasized in these studies as the origin of a strain in the structure of the neighboring particles (viz. the lattice in case of superconductors and inter-atomic bonds in liquid 3He) is a natural consequence of wave nature of particles for which a particle behaves as a WP and occupies exclusively a space of size λ/2. This is clearly supported by the experimental observation that an electron in LHe-4 and LHe-3 exclusively occupies large size spherical cavity (or what is known as electron bubble) which has a radius of the order of ≈ 19Ǻ and the volume expansion exhibited by LHe-3 on its cooling below about 0.6 K[2(a)]. In a recent paper[84], we explained that only our theory concludes an ordered arrangement of particles (free from collisions) in the S-phase of a SIB desired to explain the experimental observation of Stark effect of roton transition[85] in He-II. Evidently, the observation of Stark effect renders strong experimental support to our theory and the absence of p = 0 condensate.Our non-conventional approach works well in developing the microscopic theory of a bosonic system like LHe-4 (as discussed in this paper) and a fermionic system like electron fluid in superconductors discussed in[82] (valid also for liquid 3He type systems). We hope that a critical discussion and scientific debate on our approach may further improve its strength and accuracy and it will help in concluding the desired theory of widely different many body systems of interacting bosons and fermions.It may be noted that our theory uses only the realistic picture of a fluid. It makes no assumption such as the existence of p = 0 condensate as the origin of superfluidity used by CMT. It is, obviously, consistent with the well known philosophical principle, -the Occam’s razor, which states that the explanation of a phenomenon should make as few assumptions as possible or the simplest solution of a problem is preferable to more complicated solutions. In this context it is interesting that our theory helps in clarifying the difference between S-fluid and N-fluid states even to a layman since these states can be identified, respectively, with: (i) the ordered positions and motions of soldiers in an organized army platoon and (ii) random positions and motions of people in a crowd. While the people in the former have coherent motion with no chance of mutual collision, those in the latter have incoherent motion with high probability of such collisions. The analogy seems to agree with what has been depicted in[86] about the BEC state of atoms in TDG and what has been perceived by Leggett[87] about 4He atoms in the so called p=0 condensate in He-II but with a difference. According to our theory, all atoms in the S-state of a SIB behave like soldiers in an organized army platoon, while in view of[86,87], this analogy applies only to the atoms which constitute the so called p = 0 condensate (i.e. about 10% 4He atoms in He-II or about 60% atoms in BEC state of TDG). In summary, we succeeded in developing the long awaited microscopic theory of a SIB like LHe-4 and TDGs. It finds that superfluidity of a SIB is basically a property of its G-state configuration which persists at all T < Tλ; it can be exhibited by a SIB of any size (as small as a microscopic cluster having a few bosons or as large as bulk LHe-4) provided the system retains fluidity at To(≡ εo). The theory predicts that such a SIB would exhibit –ve thermal expansion coefficient around its transition to superfluid state. It also predicts the presence of phonon like waves of oscillations in q values around qo (proposed to be known as omon) which propagate from the points (or regions) of lower T to those of higher T. For the first time our theory underlines the importance of the WP manifestation of a quantum particle and zero point force fo exerted by each of them on the neighboring particles in organising their relative positions in r- and φ-spaces. Our similar study of N interacting bosons confined to a 1-D box[81] clearly concludes that superfluidity and related properties can also be exhibited by systems of low dimensions (viz., 1-D and 2-D) below certain T(of the order of To). The results of our theory can have meeting points with those of CMT[8, 50] provided the energy corresponding to their concluded N(p) (Fig.4(B) is minimized. This point is concluded in our recent paper[79(c)] which not only reveals the absence of p=0 condensate but also demonstrates the possibility of N (=2, 3, ...) body correlations in superfluid state of a SIB; these correlations have been central to the recent developments in CMT[43-46]. The fact that our theory has been developed by solving its N-body Schrodinger equation in its standard differential form breaks the myth that such a solution is practically impossible to achieve. It also sets aside the speculation[5] that wave mechanics does not have basic principles to explain superfluidity of He-II. We hope that this theory would be accepted widely by the physics community and in this context, we would like to submit that 75 years is a long time to test the validity of the idea of p = 0 condensate as the origin of superfluidity. It is high time to give a chance to newer ideas. Acknowledgements
- The author has no words to express his gratitude to Prof. A. J. Leggett for his valuable comments. He is thankful to N.M. Blagoveshchenskii, Bimalendu Dey, Jorge E. Hirsch, Ashok Kumar, and B. K. Srivastava, for their encouraging communication, and his students D.R. Chaudhury, S. Chutia, L. Chhangte, Ningthoujam T. Chanu, and S. Dey for their efforts to take this theory forward.
Appendix – A
- A Critical Analysis of < Aδ(x) >= 0In general A(x), in VHC(x) ≡ A(x)δ(x), can be such that A(x) → ∞ for x → 0. It can, therefore, be expressed as
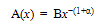 | (A-1) |
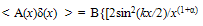 | (A-2) |
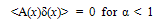 | (A-3) |
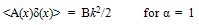 | (A-4) |
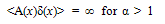 | (A-5) |
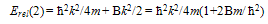 | (A-6) |
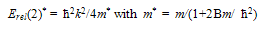 | (A-7) |
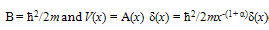 | (A-8) |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML