-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Condensed Matter Physics
p-ISSN: 2163-1115 e-ISSN: 2163-1123
2012; 2(1): 11-15
doi:10.5923/j.ajcmp.20120201.02
Photothermal Investigation of Te-Doped Bulk Gasb: Correlation between Non-Radiative Lifetime and Thermal Diffusivity
Faycel Saadallah, Sameh Abroug, Noureddine Yacoubi
Photothermal Laboratory of Nabeul, Merazka Nabeul, 8050, Tunisia
Correspondence to: Faycel Saadallah, Photothermal Laboratory of Nabeul, Merazka Nabeul, 8050, Tunisia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Photothermal deflection PTD is used in order to reveal the influence of Te doping on non radiative carrier lifetime for GaSb bulk sample when illuminated by a modulated and monochromatic light beam. Theoretical simulations are obtained from an adapted theoretical model, based on the resolution of both heat and carrier diffusion equations. Auger recombination coefficient obtained from the linear relation between lifetime and the inverse of squared concentration is in agreement with literature. Moreover, it is found that low n-doping reduces the surface recombination velocity S because of dangling bonds neutralisation at the surface. However for higher doping concentration, S is enhanced by Te doping.
Keywords: Photothermal Deflection, Lifetime, Thermal Diffusivity, Doping
Cite this paper: Faycel Saadallah, Sameh Abroug, Noureddine Yacoubi, Photothermal Investigation of Te-Doped Bulk Gasb: Correlation between Non-Radiative Lifetime and Thermal Diffusivity, American Journal of Condensed Matter Physics, Vol. 2 No. 1, 2012, pp. 11-15. doi: 10.5923/j.ajcmp.20120201.02.
Article Outline
1. Introduction
- Carrier transport mechanisms in semiconductors are widely investigated by many techniques[1-5] such as time resolved photoconductivity, photoluminescence and photoacoustic processes. Of the several techniques available for semiconductor characterization, photothermal deflection PTD[5-9] is one of the most widely used. In this case, the sample is usually irradiated by a modulated light beam. The absorbed energy is converted into heat that diffuses in the surrounding fluid causing the deflection of a probe beam skimming the sample surface. The measured deflection also called photothermal signal provides us, besides thermal and optical parameters, with carrier transport properties such as lifetime of photo-induced free carriers. Indeed, generation and recombination of minority carriers occur in a thin layer near the irradiated surface and thus has a significant contribution to the photothermal signal. In this paper, we present PTD measurement of minority carrier lifetime in doped GaSb. As the measured photothermal signal is proportional to the probe beam deflection, we should calculate the sample surface temperature since it is supposed to be proportional to this deflection. For this purpose, we propose a theoretical model based on the resolution of both heat and carrier diffusion equations. Then we fit the amplitude and phase of the theoretical deflection to those of the measured signal with bulk lifetime and surfacerecombination velocity S as adjustable parameters. The heat generated is related to the non radiative processes, and therefore the parameters that can be determined through this procedure are and S. Non radiative recombination can occur in several ways. In high quality GaSb samples, the main contribution to non-radiative carrier lifetime is most probably, the band to band recombination for which Auger process can be the dominant mechanism.
2. Theoretical Model
2.1. Principle of Photothermal Deflection
- The semiconductor sample is heated by a uniform monochromatic Light beam, modulated at the frequency F, which strikes normally at the sample surface. When the surface is uniformly illuminated, thermal wave generated by the optical absorption diffuses only in the beam direction through the sample and the surrounding fluid. The temperature variations in the fluid (air) induces a refractive index gradient which causes the deflection of a laser probe beam parallel to the sample surface passing through the fluid. This deflection could be related to thermal and carrier transport properties of the sample. The complex expression of the deflection
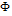 is given by[9]:
is given by[9]: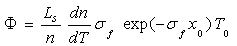 | (1) |
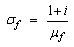 is related to thermal diffusion length
is related to thermal diffusion length 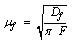 in the fluid, and T0 is the complex temperature rise at the sample surface written as:
in the fluid, and T0 is the complex temperature rise at the sample surface written as: 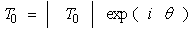 | (2) |
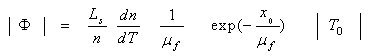 | (3) |
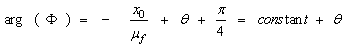 | (4) |
2.2. Determination of the Surface Temperature T0
- In order to calculate the temperature at the sample surface, we should solve the heat and carrier diffusion equations. This method has been followed in Photoacoustic investigations [10-12]. The same equations are used in PTD[12] with the assumption of optically thin sample, which is not the case in this work where bulk GaSb have been studied. In our case, as the sample (figure 1) is uniformly heated, only diffusion in the heating beam direction is considered. This assumption is satisfied if the pump beam dimensions are higher than thermal diffusion length.
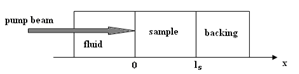 | Figure 1. Schema of the sample with a backing and the deflecting medium |
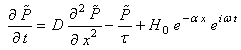 | (5) |
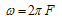 and
and 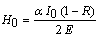 is the generation term which depends on the intensity I0 of heating beam, its energy E and the sample reflectivity R. In the other hand, the heat flow is governed by the heat conduction equation in the different media:
is the generation term which depends on the intensity I0 of heating beam, its energy E and the sample reflectivity R. In the other hand, the heat flow is governed by the heat conduction equation in the different media: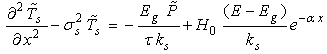 | (6) |
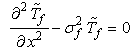 | (7) |
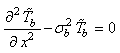 | (8) |
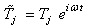 is the complex temperature in the medium j (j = f, s or b) and
is the complex temperature in the medium j (j = f, s or b) and 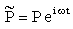 is the complex excess photo-carrier density.
is the complex excess photo-carrier density. 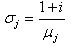 depends on thermal diffusion length
depends on thermal diffusion length 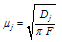 Dj and kj are respectively thermal diffusivity and conductivity of the medium j.Equation 6 show that the absorbed light energy is converted into heat throw two processes: thermalization and bulk recombination.The general solutions of the above equations are:
Dj and kj are respectively thermal diffusivity and conductivity of the medium j.Equation 6 show that the absorbed light energy is converted into heat throw two processes: thermalization and bulk recombination.The general solutions of the above equations are: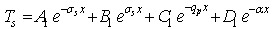 | (9) |
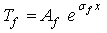 | (10) |
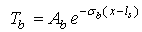 | (11) |
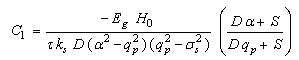 | (12) |
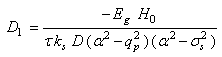 | (13) |
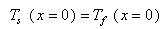 | (14) |
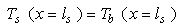 | (15) |
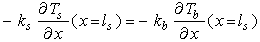 | (16) |
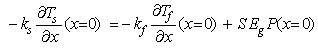 | (17) |
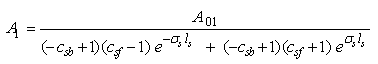 | (18) |
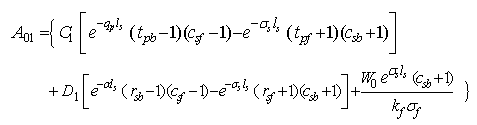 | (19) |
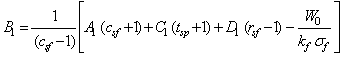 | (20) |
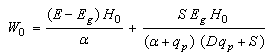 | (21) |
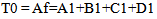 | (22) |
3. Experimental Setup
- The experimental device[8] is shown in fig.2. Monochromatic light beam is modulated with a mechanical chopper at a frequency F and focused on the sample surface. The absorption of the optical heating beam by the sample generates a thermal wave that propagates in the sample and in the deflecting fluid (air), leading to the deflection of a probe laser beam (He-Ne) skimming the sample surface. This deflection is detected with a position photodetector linked to a lock in amplifier giving us the amplitude and phase of the measured photothermal signal. The curves are drawn while varying the modulation frequency F in the range of 10–400 Hz. Indeed, some works[13] show that we can determine the transport properties and S) of bulk semiconductors in this frequency domain.
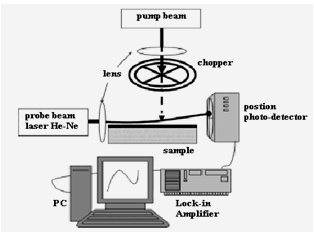 | Figure 2. Experimental setup |
4. Results and Discussions
- In this work we have investigated Te-doped and non intentionally (n.i.d.) doped commercial GaSb bulk samples. The n.i.d. is usually P type semiconductor but the doped samples are of N type. Firstly, Hall effect measurements are used to determine the free carrier concentration given in table 1.
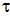 and the surface recombination velocity of the photogenerated minority carriers due to heating beam. In figures 3 and 4, are shown the experimental amplitude and phase curves for all the GaSb samples. These curves are compared to those obtained from the theoretical simulation using the above theoretical model. The best fitted theoretical curves are drawn on the same figures. Theoretical simulations show that we can easily determine surface recombination velocity S or non radiative lifetime
and the surface recombination velocity of the photogenerated minority carriers due to heating beam. In figures 3 and 4, are shown the experimental amplitude and phase curves for all the GaSb samples. These curves are compared to those obtained from the theoretical simulation using the above theoretical model. The best fitted theoretical curves are drawn on the same figures. Theoretical simulations show that we can easily determine surface recombination velocity S or non radiative lifetime 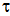 . However, the sensitivity of this model for bulk semiconductor is limited to the range of 1-107 cm s-1 for S and 10-3 - 10-10 s for
. However, the sensitivity of this model for bulk semiconductor is limited to the range of 1-107 cm s-1 for S and 10-3 - 10-10 s for 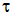 .
.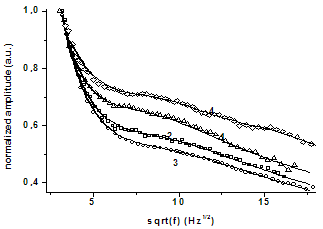 | Figure 3. Amplitude of measured photothermal signal for undoped and Te doped GaSb samples (dots), fitted with theoretical amplitude (solid line) |
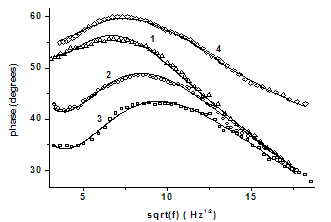 | Figure 4. Phase of measured photothermal signal for undoped and Te doped GaSb samples (dots), fitted with theoretical phase (solid line) |
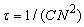 The Auger recombination coefficient obtained from the linear fit is C=3.4 10-29 cm6.s-1. This value is in the range of those measured by other authors[16].
The Auger recombination coefficient obtained from the linear fit is C=3.4 10-29 cm6.s-1. This value is in the range of those measured by other authors[16].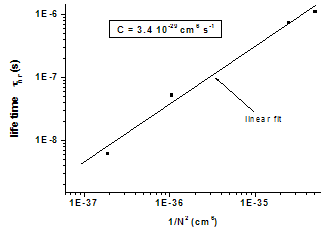 | Figure 5. Non radiative lifetime 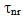 of the photoexcited carriers versus 1/N2 of the photoexcited carriers versus 1/N2 |
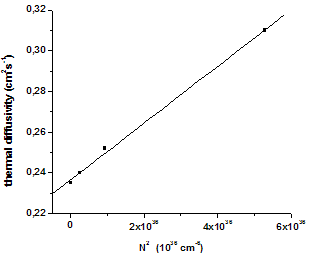 | Figure 6. Thermal diffusivity obtained from photothermal signal versus 1/N2 (N is the carrier concentration) |
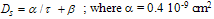 and
and 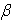 = 0.236 cm2s-1. This reveals a correlation between thermal and carrier diffusion processes which is probably due to the predominance of free carriers contribution to heat transport.
= 0.236 cm2s-1. This reveals a correlation between thermal and carrier diffusion processes which is probably due to the predominance of free carriers contribution to heat transport.5. Conclusions
- Photothermal deflection is used in order to determine surface recombination velocity and non-radiative life time for bulk GaSb semiconductor. For this purpose, the two components (phase and amplitude) of the measured photothermal signal are compared to the corresponding theoretical curves. The results show that while increasing of doping concentration, lifetime decreases and surface recombination velocity increases. On the other hand we have revealed a correlation between non radiative lifetime and thermal diffusivity, this proves the predominance of free carriers contribution to both heat and electronic transport processes.
References
| [1] | S. Anikeev, D. Doetsky, G. Belenky, and S. Luryi, C. A. Wang, J. M. Borrego, G. Nichols, “Measurement of the Auger recombination rate in p-type 0.54 eV GaInAsSb by time resolved photoluminescence”, Appl. Phys. Lett. 83 (16), 3317-3319 (2003) |
| [2] | Z. H. Chen, R. Bleiss, A. Mandelis, A. Buczkowski and F. Shimura,”Photothermal rate- window spectrometry for non- contact bulk lifetime measurements in semiconductors”, J. Appl. Phys. 73 (10), 5043-5048 (1993) |
| [3] | F. Saadallah, N. Yacoubi, F. Genty and C. Alibert, “ Investigation of thermal and optical properties of distributed Bragg reflectors by photothermal deflection spectroscopy” Appl. Opt. 41, 7561-7568 (2002) |
| [4] | D. M. Todorovic, P. M. Nicolic, M. D. Dramicanin, D. G. Vasiljevic, and Z. D. Ristovski, “Photoacoustic frequency heat transmission technique: thermal and carrier transport parameters measurements in silicon”, J. Appl. Phys. 78, 5750-5755 (1995) |
| [5] | Jordi Sancho-Parramon, Josep Ferré-Borrull, Salvador Bosch, Anna Krasilnikova, and Jiri Bulir,”New calibration method for UV-VIS photothemal deflection spectroscopy set-up”, Appl. Surface Science 253 (1), 158-162 (2006) |
| [6] | A. N. Petrovsky, A. O. Salnick, V. V. Zuev, V. V. Grigoryev, and M. M. Mekhtiev, in Photothermal and Photoacoustic Phenomena III, edited by D. Bicanic springer series in Optical Sciences, vol.69,( Springer, Berlin, Heidelberg 1992) p. 390 |
| [7] | C. Khélia, K. Boubaker, T. Ben Nasrallah, M. Amlouk, S. Belgacem, F. Saadallah, N. Yacoubi,”Morfological and thermal properties of  SnS2 crystals grown by spray pyrolysis technique” J. Crystal Growth 311 (4), 1032-1035 (2009) SnS2 crystals grown by spray pyrolysis technique” J. Crystal Growth 311 (4), 1032-1035 (2009) |
| [8] | F. Saadallah, N. Yacoubi, F. Genty and C. Alibert,” Photothermal investigation of thermal and optical properties of GaAlAsSb and AlAsSb thin layers” J. Appl. Phys. 94 (8), 5041-5048 (2003) |
| [9] | J. C. Murphy and L. C. Aamodt,”Photothermal Spectroscopy using Optical Beam Probing: Mirage Effect" J. Appl. Phys.51, 4580-4588 (1980) |
| [10] | I. Delgadillo, M. Vargas, A. Cruz-Orea, J. J. Alvarado-Gil, R. Baquero, F. Sanchez-Sinencio, H. Varg, “Photoacoustic CdTe surface characterization”, Appl. Phys. B. 64, 97-101 (1997) |
| [11] | E. Marın, I. Riech, P. Dıaz, J. J. Alvarado-Gil, R. Baquero, J. G. Mendoza-Alvarez, H. Vargas, A. Cruz-Orea and M. Vargas, “Photoacoustic determination of non-radiative carrier lifetimes”, J. Appl. Phys. 83 (5), 2604-2609 (1998) |
| [12] | Anita R. Warrier, Tina Sebastian, C. Sudha Kartha, and K. P. Vijayakumar, “Transverse photothermal beam deflection technique for determining the transport properties of semiconductor thin films”, J. Appl. Phys. 107, 073701 (2010) |
| [13] | A. Pinto Neto, H. Vargas, N.F. Leite and L.C.M. Miranda, “Photoacoustic investigation of semiconductors: influence of carrier diffusion and recombination in PbTe and Si”, Phys. Rev.B. 40 (6), 9971-9979 (1989) |
| [14] | I. Reich, P. Diaz, and E. Marian, “Study of non radiative recombination mechanisms in semiconductors by photoacoustic measurements”, Phys. Stat. Sol. (b) 220, 305-308 (2000) |
| [15] | Sajan. D. George, Dilna. S. P. Radhakrishnan, C. P. G. Vallabhan, and V. P. N. Nampoori, “ Photoacoustic measurement of transport properties in doped GaAs epitaxial layers”, Phys. Stat. Sol. (a) 195 (2), 416-421 (2003) |
| [16] | A. Joullié, “New developments in mid-infrared Sb-based lasers”, J. Phys. France 9 (1999), Pr2-79 – Pr2-95 |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML