-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2024; 14(1): 1-14
doi:10.5923/j.ajcam.20241401.01
Received: Jan. 24, 2024; Accepted: Feb. 17, 2024; Published: Feb. 29, 2024

Application of the Modied Adomian Decomposition Method on a Mathematical Model of COVID-19
Justina Mulenga, Patrick Azere Phiri
Mathematics Department, School of Mathematics and Natural Sciences, The Copperbelt University, Kitwe, Zambia
Correspondence to: Justina Mulenga, Mathematics Department, School of Mathematics and Natural Sciences, The Copperbelt University, Kitwe, Zambia.
| Email: |  |
Copyright © 2024 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this study, we constructed and analysed a mathematical model of Covid-19 in order to comprehend the transmission dynamics of the disease. The reproduction number (RC) was calculated via the next generation matrix. We also used the Lyaponuv method to show the global stability of both the disease free and endemic equilibrium point. The results showed that the disease-free equilibrium point is globally asymptotically stable if RC<1 and the endemic equilibrium point is globally asymptotically stable if RC>1. We further used the Adomian decomposition method and the modified Adomian decomposition method to obtain the solutions of the model. Numerical analysis of the model was done using Sagemath 9.0 software.
Keywords: COVID-19, Stability analysis, Equilibrium points, Adomian decomposition method, Modified Adomian decomposition method, Numerical analysis
Cite this paper: Justina Mulenga, Patrick Azere Phiri, Application of the Modied Adomian Decomposition Method on a Mathematical Model of COVID-19, American Journal of Computational and Applied Mathematics , Vol. 14 No. 1, 2024, pp. 1-14. doi: 10.5923/j.ajcam.20241401.01.
Article Outline
1. Introduction
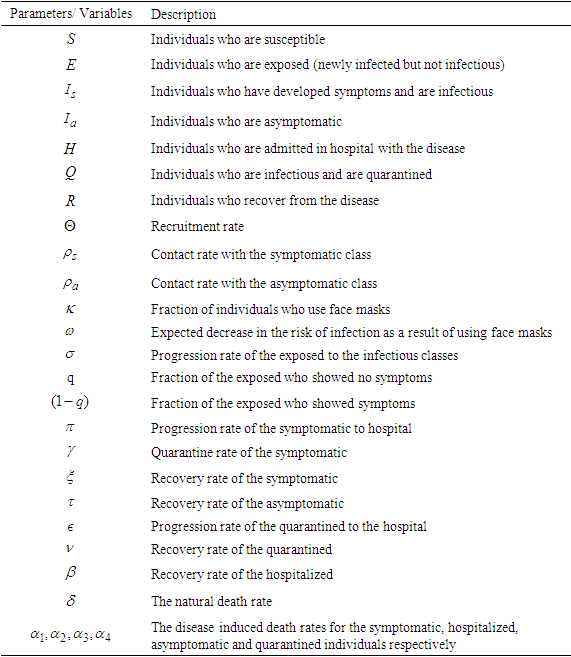
- Mathematical disease models are important tools in analyzing the spread and the control of infectious diseases. These models are based on dividing the host population into compartments, each containing individuals that are identical in terms of their status with respect to the disease under consideration. For example, in the SIR model there are three compartments namely Susceptibles (S), Infections (I) and Removed (R). From the compartments, the set of equations will arise. The equations specify how the sizes of the compartment change overtime, and are linear and nonlinear. Solutions of these equations will yield, S(t) the size of susceptibles at time t, I(t) the size of infectious individuals at the time t, and R(t) the size of the removed population at a given time t. Solving nonlinear equations is more challenging than solving linear equations. Different authors use different methods to solve nonlinear equations.In [1], Homotopy Analysis Method (HAM) was used to solve the differntial equations of the Susptible, Exposed, Infectious and Removed (SEIR) epidemic model. The results showed that the series solution converged very fast and the solutions were accurate. The Adomian Decomposition Method (ADM) was used to solve the mathematical model of malaria in [2]. The Laplace Adomian Decomposition Method (LADM) was applied to analyse the SEIR epidemic models of measles in [3]. In [4], the ADM was employed to solve the Human Immunodeficiency Virus (HIV) infection model of latently infected cells. In [5], the Laplace-Adomian decomposition method and the Homotopy perturbation techniques were used to obtain approximate solutions of the equation of the fractional dynamics of a corona virus mathematical model under a Caputo derivative.The novel corona virus, also known as COVID-19, is a deadly disease which came into being in late 2019. It is believed to have originated from Wuhan city in China [6]. As of 23rd May 2022, it had affected 227 countries with a total of 527, 804, 291 cases worldwide and 6,300,525 deaths [7]. Infected individuals present with fever, coughing, and sneezing as some of the symptoms. In severe cases, patients are diagnosed with pneumonia and shortness of breath. It is transmitted from human to human by inhaling droplets exhaled through normal breathing, coughing, and sneezing from infected persons [8]. Approximate incubation period is from 2-14 days from the time of contact. However, it may go up to 27 days. As for the asymptomatic individuals, they do not develop any symptoms and are not aware of their infection, yet they can transmit the disease, [9]. As a result, preventive measures such as lock-down policy, use of face masks in public places, washing of hands with soap, and using hand sanitizer were introduced in most affected countries.This study focuses on the construction of a mathematical model to analyze the transmission dynamics of COVID-19 and solve it with modified Adomian decomposition method. The rest of the paper is organized as follows: in Section 2 we formulate the mathematical model of COVID-19 and analyze it. In section 3 we solve the mathematical model of COVID-19 using Adomain Decomposition Method (ADM) and Modified Adomian Decomposition Method (MADM). Section 4 presents the numerical analysis of the model and discussion. The conclusion comes in Section 5.
2. Model Formulation
- The mathematical model of COVID-19 is developed by dividing the total population
 into seven classes. The variables Susceptible
into seven classes. The variables Susceptible 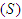 , Exposed
, Exposed 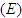 , Symptomatic
, Symptomatic 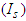 , Asymptomatic
, Asymptomatic 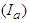 , Hospitalized
, Hospitalized 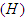 , Quarantined
, Quarantined 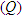 and Recovered
and Recovered 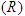 are used to represent the classes. Individuals are recruited into the susceptible class through the rate
are used to represent the classes. Individuals are recruited into the susceptible class through the rate  . The susceptible population is exposed to the disease through contact with symptomatic and asymptomatic infectious individuals. The parameters
. The susceptible population is exposed to the disease through contact with symptomatic and asymptomatic infectious individuals. The parameters 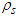 and
and 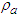 represent the effective contact rates for individuals in the symptomatic and asymptomatic infectious classes, respectively. There is a fraction of individuals who use face masks in the population and it is given as
represent the effective contact rates for individuals in the symptomatic and asymptomatic infectious classes, respectively. There is a fraction of individuals who use face masks in the population and it is given as 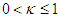 , whereas
, whereas 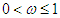 represents the expected decrease in the risk of infection as a result of using face masks. The exposed individuals progress to infectious classes at the rate
represents the expected decrease in the risk of infection as a result of using face masks. The exposed individuals progress to infectious classes at the rate 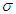 . A fraction
. A fraction 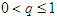 of the exposed shows no symptoms and they proceed to asymptomatic infectious class whereas the remaining fraction
of the exposed shows no symptoms and they proceed to asymptomatic infectious class whereas the remaining fraction 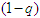 shows symptoms of the disease and hence proceeds to the symptomatic class. The symptomatic infectious are hospitalized at the rate of
shows symptoms of the disease and hence proceeds to the symptomatic class. The symptomatic infectious are hospitalized at the rate of 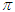 and are quarantined at the rate of
and are quarantined at the rate of 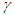 . The asymptomatic infectious recover at the rate
. The asymptomatic infectious recover at the rate 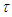 . The quarantined are hospitalized at the rate
. The quarantined are hospitalized at the rate 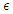 and they recover at the rate
and they recover at the rate 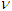 whereas the hospitalized recover at the rate
whereas the hospitalized recover at the rate 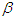 . There is a natural death rate of
. There is a natural death rate of 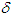 for individuals in all classes. Additionally, individuals in the symptomatic, hospitalized, asymptomatic, and quarantined classes have disease-induced death rates of
for individuals in all classes. Additionally, individuals in the symptomatic, hospitalized, asymptomatic, and quarantined classes have disease-induced death rates of 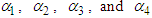 , respectively. The summary of the description of the variables and parameters is given in Tables 1. Using the symbols and variables described in Table 1 we draw the compartmental model that shows the progression of the disease, given in Figure 1.
, respectively. The summary of the description of the variables and parameters is given in Tables 1. Using the symbols and variables described in Table 1 we draw the compartmental model that shows the progression of the disease, given in Figure 1.
|
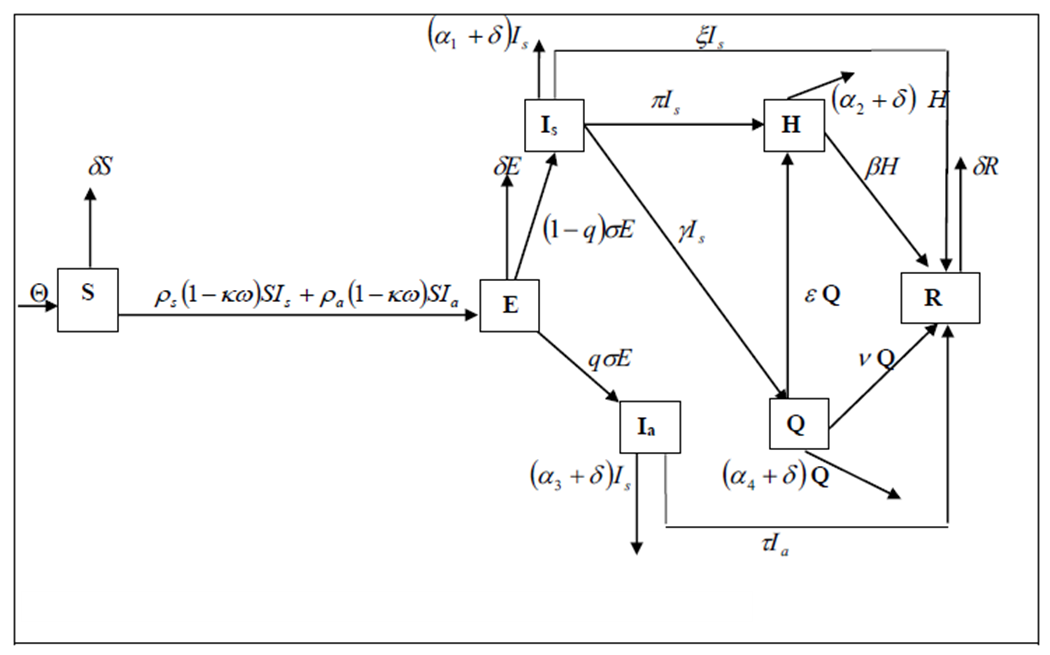 | Figure 1. Compartmental model of the transmission of COVID-19 |
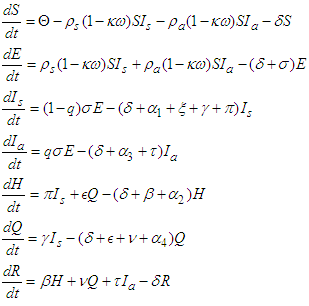 | (1) |
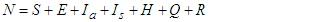 | (2) |
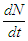 is given by
is given by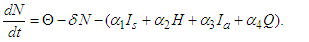 | (3) |
2.1. Positivity and Boundedness of Solutions
2.1.1. Positivity of Solutions
- Since the variables of model equation system (1) represent humans, it is important to show that they are positive. Theorem 1 If the initial values are given by
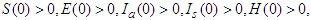
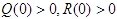 then the solutions
then the solutions 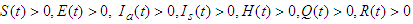 of the system equation (1) are positive for all
of the system equation (1) are positive for all 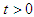 .Proof: Using the first equation of equation system (1), we have the following:
.Proof: Using the first equation of equation system (1), we have the following: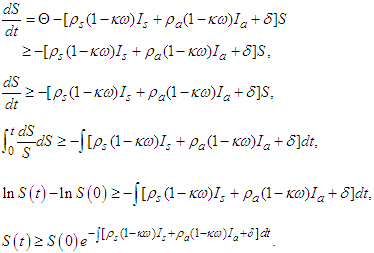 Thus
Thus 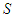 is positive since
is positive since 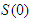 is positive and the exponential function
is positive and the exponential function 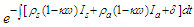 is always positive. Using the same method, we can prove the rest of the equations of system equation (1) and show that
is always positive. Using the same method, we can prove the rest of the equations of system equation (1) and show that 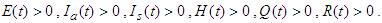
2.1.2. Boundedness of the Solutions
- Theorem 2 All positive solutions presented in Theorem (1) are bounded.Proof: In the absence of the disease, i.e
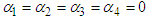 , equation (3) becomes
, equation (3) becomes 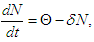 which can be written as
which can be written as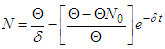 , and as
, and as 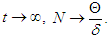 Thus, we conclude that
Thus, we conclude that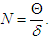 | (4) |
2.2. Existence and Stability of Equilibrium Points
- The equilibrium points are calculated by equating the left hand side of equation system (1) to zero. This leads to the following system of equations,
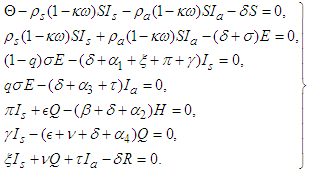 | (5) |
2.2.1. The Disease Free Equilibrium Point (dfep)
- In the absence of infection
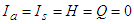 . Solving the equations of system 5, we obtain
. Solving the equations of system 5, we obtain 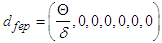 .
.2.2.2. The Reproduction Number of the Model
- We compute the basic reproduction number RC of the model system (1) by following [10]. The basic reproduction number measures the average number of new infections generated by a single infected person in a completely susceptible population. Using the next generation matrix, we consider the classes that are actively transmitting the disease. These are:
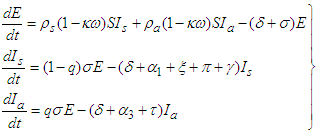 | (6) |
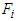 and
and 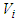 which are the rate of appearance of new infections in compartment
which are the rate of appearance of new infections in compartment 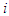 and transfer of individuals into and out of compartment
and transfer of individuals into and out of compartment 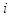 by all other means, respectively. Here
by all other means, respectively. Here 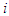 represents the infected classes, i. e
represents the infected classes, i. e 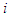
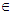 1, 2, 3. Thus we obtain,
1, 2, 3. Thus we obtain, 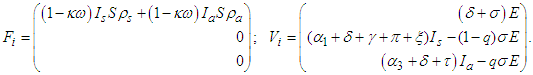 Then taking partial derivatives of both
Then taking partial derivatives of both 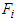 and
and 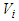 on the disease-free equilibrium point we get,
on the disease-free equilibrium point we get,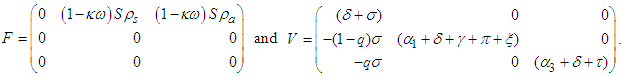 Next we calculate the inverse of
Next we calculate the inverse of 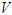 which is given by:
which is given by: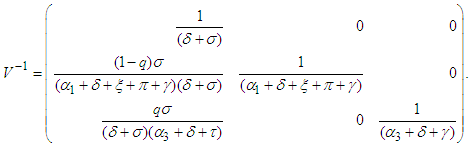 The next generation matrix is given as the following product:
The next generation matrix is given as the following product: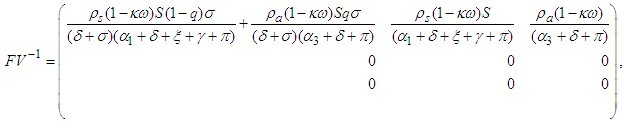 and we calculate the eigenvalues of
and we calculate the eigenvalues of 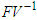 as follows:
as follows: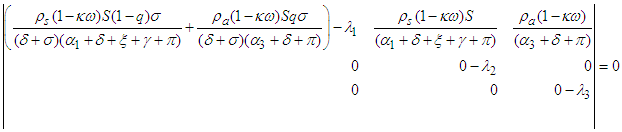 Thus
Thus 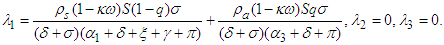 The reproduction number is given by the largest eigenvalue of the determinant of the matrix
The reproduction number is given by the largest eigenvalue of the determinant of the matrix 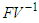 and so
and so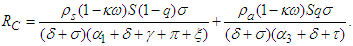 | (7) |
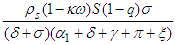 defines the number of new COVID-19 cases generated from the symptomatic infected individuals in class
defines the number of new COVID-19 cases generated from the symptomatic infected individuals in class 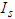 . The second reproduction number is
. The second reproduction number is 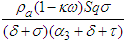 which defines the number of new COVID-19 cases generated from the asymptomatic infectious individuals in class
which defines the number of new COVID-19 cases generated from the asymptomatic infectious individuals in class 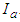 Hence the reproduction number is written as,
Hence the reproduction number is written as,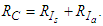 | (8) |
2.2.3. Global Stability of the Disease-Free Equilibrium Point
- The global stability of the disease-free equilibrium
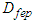 is established by the following theorem.Theorem 3 If
is established by the following theorem.Theorem 3 If 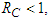 the disease-free equilibrium is globally asymptotically stable in
the disease-free equilibrium is globally asymptotically stable in 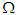 and unstable if
and unstable if 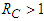 We will use the Lyapunov function to show the stability of the disease-free equilibrium. Let the Lyapunov function be
We will use the Lyapunov function to show the stability of the disease-free equilibrium. Let the Lyapunov function be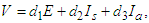 | (9) |
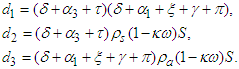 Let
Let 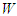 be the region that contains the origin. The we note that,(i)
be the region that contains the origin. The we note that,(i) 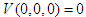 ,(ii)
,(ii) 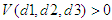 for all d1,d2,d3
for all d1,d2,d3 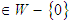 since,
since,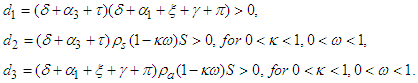 Also
Also 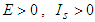 and
and 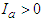 .Thus we conclude that
.Thus we conclude that 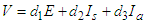 is positive definite.We now prove the stability of the disease-free equilibrium point using the Lyapunov function.Proof: From equation (9), the derivative is given as
is positive definite.We now prove the stability of the disease-free equilibrium point using the Lyapunov function.Proof: From equation (9), the derivative is given as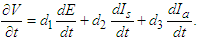 | (10) |
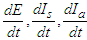 are given in equation system (1). Therefore,
are given in equation system (1). Therefore,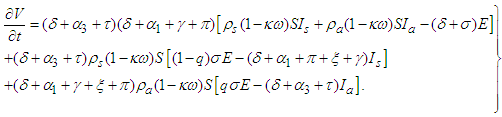 | (11) |
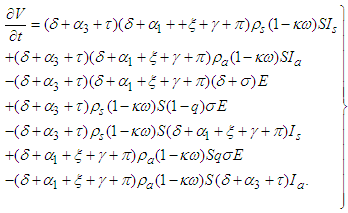 | (12) |
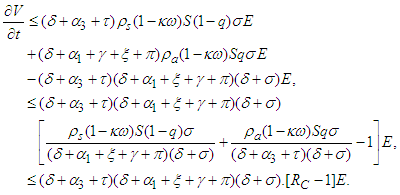 Hence,
Hence, 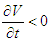 if
if 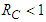 and
and 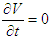 if
if 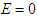 . By LaSalle's Invariance Principle [11], we conclude that the disease-free equilibrium
. By LaSalle's Invariance Principle [11], we conclude that the disease-free equilibrium 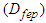 of the model of COVID-19 is globally asymptotically stable in
of the model of COVID-19 is globally asymptotically stable in 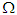 whenever
whenever 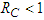
2.2.4. The Endemic Equilibrium Point
- The endemic equilibrium point is denoted by
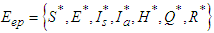 and is calculated as,
and is calculated as,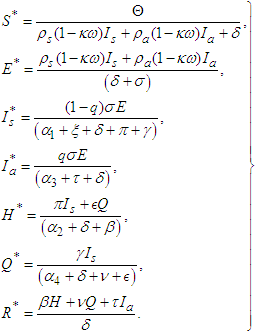 | (13) |
2.2.5. Global Stability Analysis of the Endemic Equilibrium Point
- The Lyapunov asymptotic stability theorem is used to prove the global asymptotic stability of the endemic equilibrium point. Using the method for constructing the Lyapunov function discussed in [12], we formulate the Lyapunov function for model equation (1).Theorem 4 If
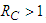 , then the endemic equilibrium point
, then the endemic equilibrium point 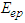 of model equation (1) is globally asymptotically stable in the region
of model equation (1) is globally asymptotically stable in the region 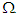 Proof First, we define
Proof First, we define 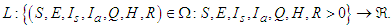 Consider the function below:
Consider the function below: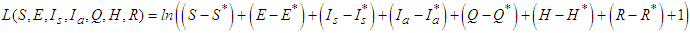 | (14) |
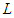 along the solutions of the model in equation (1) is given by the expression:
along the solutions of the model in equation (1) is given by the expression: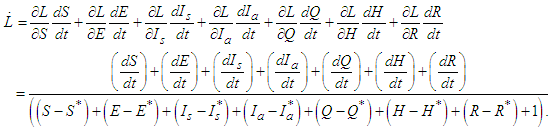 | (15) |
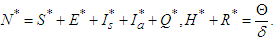 | (16) |
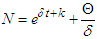 where,
where, 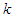 is the value that satisfies the condition
is the value that satisfies the condition 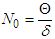 . Thus
. Thus 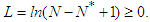 Therefore,
Therefore,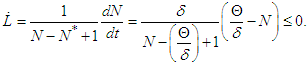
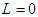 and
and 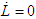 are satisfied if and only if
are satisfied if and only if 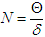
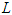 is positive definite and
is positive definite and 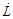 is negative definite, hence the function
is negative definite, hence the function 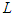 is the Lyapunov function for model equation (1) and the endemic equilibrium
is the Lyapunov function for model equation (1) and the endemic equilibrium 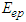 is globally asymptotically stable by the Lyapunov asymptotic stability analysis [13]. Hence the proof.
is globally asymptotically stable by the Lyapunov asymptotic stability analysis [13]. Hence the proof.3. Adomian Decomposition Method
- In this section we apply the Adomian decomposition method proposed by George Adomian in the mid 1980's, [14] to solve the system equation (1).
3.1. Basic Concepts of the Adomian Decomposition Method
- Let us consider the initial value problem expressed as
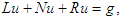 | (17) |
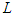 is the linear operator,
is the linear operator, 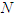 is the nonlinear operator and
is the nonlinear operator and 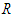 is the remaining linear part. By defining the inverse operator of
is the remaining linear part. By defining the inverse operator of 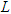 as
as 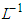 , we introduce it on both sides of equation (17) to get,
, we introduce it on both sides of equation (17) to get, 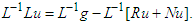 | (18) |
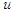 in equation (18) leads to,
in equation (18) leads to,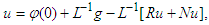 | (19) |
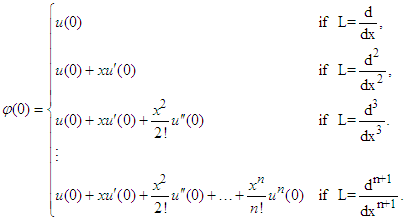 The Adomian Decomposition Method assumes that the unknown function
The Adomian Decomposition Method assumes that the unknown function 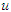 can be expressed by an infinite series of the form,
can be expressed by an infinite series of the form,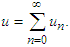 | (20) |
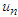 will be determined recursively. This method also defines the nonlinear term by the Adomian polynomials. More precisely, the ADM assumes that the nonlinear operator can be decomposed by an infinite series of polynomials given by,
will be determined recursively. This method also defines the nonlinear term by the Adomian polynomials. More precisely, the ADM assumes that the nonlinear operator can be decomposed by an infinite series of polynomials given by,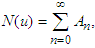 | (21) |
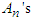 are the Adomian's polynomials defined as,
are the Adomian's polynomials defined as, 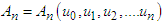 | (22) |
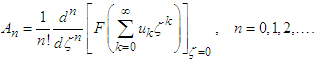 | (23) |
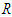 is a linear operator we obtain,
is a linear operator we obtain,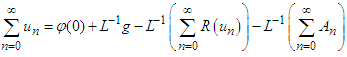 | (24) |
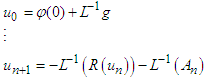 | (25) |
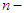 term approximation of the solution is given by,
term approximation of the solution is given by,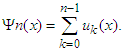 | (26) |
3.1.1. Solutions of the Mathematical Model of COVID-19 Using Adomian Decomposition Method
- In order to explicitly construct approximate solutions of the system described by equation (1), we employ the Adomain decomposition method. To apply the Adomian decomposition method we choose:
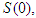
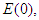
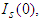
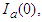
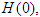
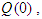
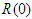 as initial approximations of
as initial approximations of 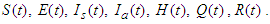 Using equation (12) for calculating the Adomian polynomials for
Using equation (12) for calculating the Adomian polynomials for 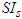 and
and 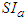 as
as 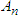 and
and 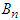 respectively, we apply equation (24) to each of the equations in model system (1) to obtain the recursive algorithm for each equation as follows:
respectively, we apply equation (24) to each of the equations in model system (1) to obtain the recursive algorithm for each equation as follows: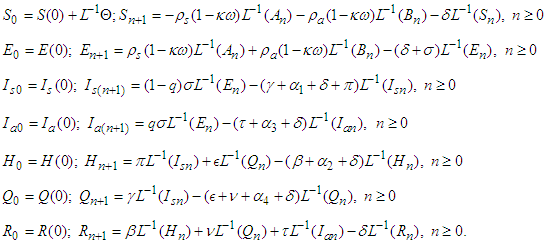 Using equation (26) the solutons to equation (1) are obtained.
Using equation (26) the solutons to equation (1) are obtained.3.2. The Modified Adomian Decomposition Method
- Here, we present the Modified Adomian Decomposition Method (MADM) which we use to solve the system of equations arising from the mathematical model of COVID-19. In [16], the authors proposed the modification of the ADM by introducing the terms
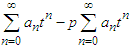 into the calculations of the standard ADM. To understand the procedure of MADM we consider equation (23) and insert
into the calculations of the standard ADM. To understand the procedure of MADM we consider equation (23) and insert 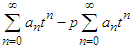 to obtain:
to obtain: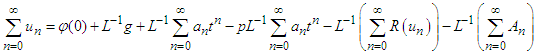 | (27) |
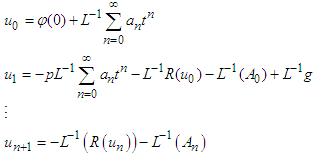 | (28) |
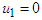 and
and 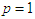 so that we solve for the coefficients
so that we solve for the coefficients 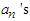 for
for 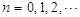 . The approximation of the solution is found by replacing the coefficients in the solution equation given by:
. The approximation of the solution is found by replacing the coefficients in the solution equation given by: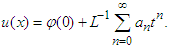 | (29) |
3.2.1. Solution of the Mathematical Model of COVID-19 using the Modified Adomian Decomposition Method
- Applying equation (27) on each equation of system (1), we obtain the recursive relationship for each equation as follows:
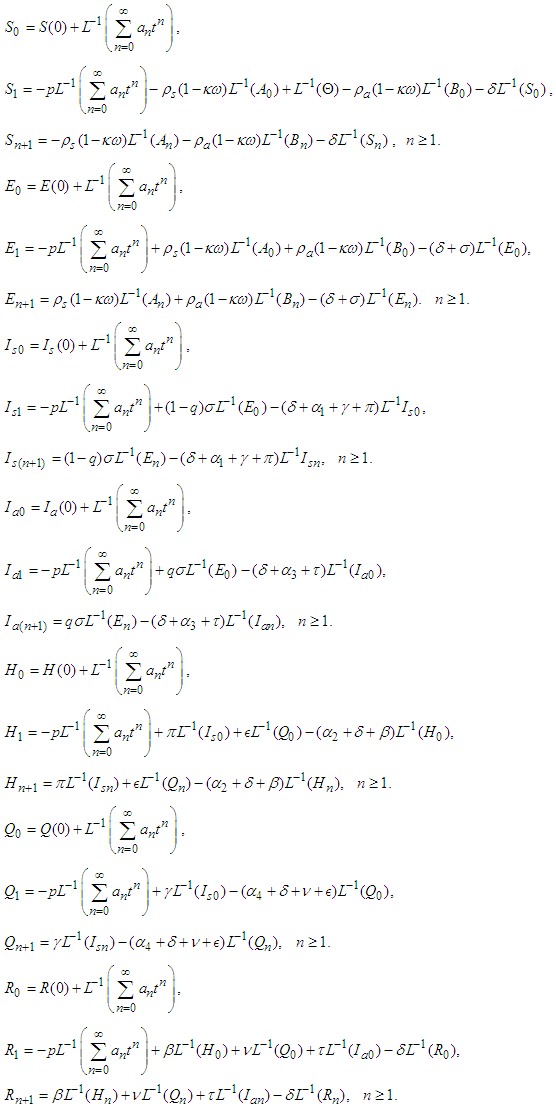 Letting
Letting 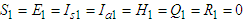 and setting
and setting 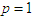 we find the
we find the 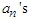 for
for 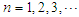 . and replace in equation (29) to write the solution for equation system (1).
. and replace in equation (29) to write the solution for equation system (1).4. Results and Discussion
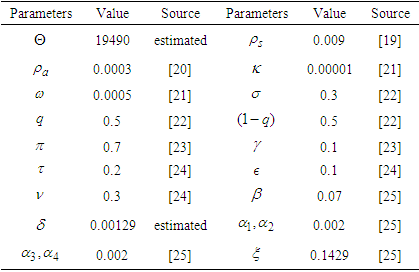
- The results obtained from solving system equation (1) using ADM are compared with the results obtained using MADM.We will use COVID -19 data for Zambia [17] as initial values and are given as
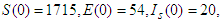
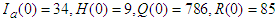 . The natural death rate,
. The natural death rate, 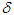 is calculated by taking the reciprocal of the average life expectancy (in months). In Zambia the life expectancy is 64.70 years [18], hence
is calculated by taking the reciprocal of the average life expectancy (in months). In Zambia the life expectancy is 64.70 years [18], hence 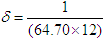 . The population of Zambia is
. The population of Zambia is 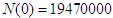 [18]. Thus the recruitment
[18]. Thus the recruitment 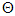 is estimated as
is estimated as 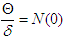 . The rest of the parameters are estimated from the literature as given in Table 2. Using the initial values and the parameter values we draw the graphs using SageMaths 9.0 software. The results are shown in Figure 2(a) to Figure 2(g).
. The rest of the parameters are estimated from the literature as given in Table 2. Using the initial values and the parameter values we draw the graphs using SageMaths 9.0 software. The results are shown in Figure 2(a) to Figure 2(g).
|
 | Figure 2(a-g) |
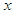 that are around zero. It is important to mention that for larger values of
that are around zero. It is important to mention that for larger values of 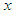 , the graphs are further away from each other.In Figure 2(b), it is clearly seen that MADM and ADM solutions are in good agreement with each other for values of
, the graphs are further away from each other.In Figure 2(b), it is clearly seen that MADM and ADM solutions are in good agreement with each other for values of 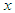 close to zero and one.Figure 2(c), Figure 2(d), Figure 2(e), Figure 2(f) and Figure 2(g) indicate that MADM and ADM solutions are the same by coincidence.The numerical analysis shown in the Figures above demonstrate the effectiveness of the modified Adomian decomposition method. The method gives highly accurate solutions with use of the first and second iterations only.
close to zero and one.Figure 2(c), Figure 2(d), Figure 2(e), Figure 2(f) and Figure 2(g) indicate that MADM and ADM solutions are the same by coincidence.The numerical analysis shown in the Figures above demonstrate the effectiveness of the modified Adomian decomposition method. The method gives highly accurate solutions with use of the first and second iterations only.5. Conclusions
- The model of COVID-19 has been formulated and its dynamical behaviour investigated. We showed that the population classes are non-negative. Using the next generation matrix, we calculated the basic reproduction number, RC, which is useful in guiding control strategies. By constructing Lyapunov functions, we proved global stability of disease free and endemic equilibrium points. If the basic reproduction number is less 1, all solutions converge to the disease free equilibrium point and the disease dies out from the population. When the basic reproduction number is greater than 1, the endemic equilibruim point is globally stable, meaning that the disease will persist and the number of infected individuals tends to a positive constant. Lastly, it is well known that analytical solutions of nonlinear ordinary differential equations are difficult to find. In this paper, we solved nonlinear and linear Ordinary Differential Equations (ODEs) using ADM and MADM. It can be seen from numerical solutions in Fiqure 2 that we demonstrated the ability of ADM and MADM in solving ODEs. The series solutions converge very rapidly and from the graphs in Figure 2(a) to Figure 2(g), we can conclude that the ADM and MADM are very efficient and accurate methods in solving nonlinear mathematical models. Data Availability: The data used to support the findings of this study is indicated within the article. Conflict of interest: No potential conflict was reported by the authors.Funding: This research did not receive any specific grant from funding agencies in the public, commercial or not-for-profit sectors.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML