Mečislovas Mariūnas
Department of Biomechanical Engineering, Vilnius Gediminas Technical University, Vilnius LT, Lithuania
Correspondence to: Mečislovas Mariūnas, Department of Biomechanical Engineering, Vilnius Gediminas Technical University, Vilnius LT, Lithuania.
| Email: |  |
Copyright © 2023 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
This article presents ways to determine the frequencies of a nonlinear dynamic system with the largest vibration amplitudes. It is shown that in the latter system, a potential frequency space is generated and it is not changing for each frequency and magnitude of the excitation force. Its parameters depend only on the size of the main parameters of the nonlinear dynamic system. The method of the spectral density space of the frequency band was used to study the magnitude of the excitation force and its frequency influence on the maximum vibration amplitudes. It has been determined that if the frequency of the excitation force or its magnitude changes, conditions are created in the system for a jump in the size of the vibration and a change in its frequency spectrum, and the vibration level can increase several tens of times. The dual response of the nonlinear dynamic system to the magnitude of the excitation force has been determined. Some necessary requirements for a dynamic system to work stably and at a minimum level of vibration are clarified. It was determined that there are three types of frequencies in a nonlinear dynamic system: resonance frequencies of systems and subsystems, parametric vibration frequencies and dynamic system vibration frequencies. The difference between resonant frequencies and parametric vibration frequencies is clarified. The possibilities of significantly reducing the level of vibrations in the system without the use of a vibration damper are explained and demonstrated. It is shown that when the degree of nonlinearity of the dynamic system is greater than 2, then the vibration frequencies in the nonlinear dynamic system are identical to the parametric vibration frequencies. The validity of the results and conclusions in the article was verified by numerical calculations.
Keywords:
Method, One degree, Excitation, Force, Nonlinear, Second, Third, Fourth, Fifth orders of nonlinearity, Resonant, Parametric, Frequencies, Magnitude, Vibration, Spectral density, Space, Frequency band, Dual response
Cite this paper: Mečislovas Mariūnas, Investigation of the Influence of Excitation Force Frequency and Magnitude on the Vibration Intensity in a Nonlinear Dynamic System, American Journal of Computational and Applied Mathematics , Vol. 13 No. 2, 2023, pp. 36-44. doi: 10.5923/j.ajcam.20231302.02.
1. Introduction
Various mathematical models are used for nonlinear dynamic system vibration study andamping: approximate analytical and numerical. In various research works, the authors use different approximate methods to solve the system of differential equations of the nonlinear dynamic model. The work [1-2] presents the methods of global estimation and local calculation of nonlinear dynamic systems. Starting from classical asymptotic, finite difference and weighted residual methods, typical methods for solving nonlinear dynamical systems are examined. In addition, new high-performance methods are proposed, such as time-domain vibration and local variation iteration. The work summarizes and develops computational methods for strongly nonlinear dynamic systems and considers the practical application of the methods within aerospace engineering. The harmonic balance method is used in works [4-5]. In [6], the theory of nonlinear systems of the Volterra series is used to analyze the magnitude of vibrations in a nonlinear dynamic system and to study their damping possibilities. The latter article provides a definition of resonances and resonant frequencies for nonlinear systems to reveal that all higher-order nonlinear output frequency response functions typically have more than one resonance, which typically occurs when the driving frequency is ωL, ωL 2/1, ωL 3 / 1, ωL 4/1 etc., where ωL is the natural frequency of the system. However, their nature was not determined in the last work. It seems that the authors are talking only about some cases of parametric excitation frequencies. The harmonic balance method is used to study large dynamic systems of cubic nonlinearity that are affected by harmonic excitation [7]. In [8-9], a method for calculating the periodic solutions of nonlinear mechanical systems with analytical nonlinearity is proposed. Nonlinear modes for Hamiltonian systems are introduced; normal forms simplify the analysis of bifurcation. It is shown how to extend, the modal synthesis procedure: the proposed nonlinear modes obtained from free vibrations are used to construct a superposition technique to describe the forced response of harmonically excited systems. The paper [10] presents an effective frequency domain method for bifurcation analysis of nonlinear dynamic systems. The proposed method involves direct tracking of bifurcation points when a system parameter, such as the level of vibration or nonlinearity, is changed. For this purpose, the so-called extended system, which includes the equation of motion and an additional equation describing the bifurcation of interest, is solved by the harmonic balance method, together with the arc length continuation technique. In [11], a frequency domain-based numerical and analytical method is used to study nonlinear dynamic systems. In [13], a full nonlinear model is developed for the dynamics of a hanging tubular cantilever that is simultaneously subjected to internal and external axial flows. A nonlinear equation of motion for the cantilever is obtained via Hamilton’s principle to third-order accuracy. The equation of motion is then discretized and solved using the pseudo-arc length continuation method. In [14], the analysis of nonlinear dynamic systems is simplified by the fact that they show no jump or bifurcation behavior, and indeed can often be well represented by an equivalent linear system, whose damping parameters depend on the form and amplitude of the excitation, in a “quasi-linear” model. The power dissipation of the equivalent linear damper, for both sinusoidal and random cases, matches that dissipated by the nonlinear damper, providing both a firm theoretical basis for this modeling approach and clear physical insight. In scientific works [15-19], the resonant frequencies of nonlinear dynamic systems are studied by approximate and numerical methods, and experimentally, which do not fully reveal their nature. The determined resonant frequencies are a mixture of resonant and parametric frequencies. The resonant property is that they are not repeatable to each other. So, all the methods mentioned above are approximate. With the help of the latter method, it is not possible to fully clarify the resonant frequency of the system and subsystems. It is also not possible to determine the causes of the occurrence of parametric vibrations in the dynamic system and their frequency. In the recent research works, the possibility of reducing the level of vibration by using the properties of a nonlinear dynamic system has not been completely clarified. In [20,21] the vibrations of one and two degrees of freedom of nonlinear dynamic systems are investigated, the frequencies of resonant and parametric vibrations are determined and it is shown that it is difficult to obtain a proper result by roughly selecting system parameters without understanding the processes in the system. The results also demonstrate that the system generates a very wide spectrum of parametric excitation frequencies. However, in the recent work, methods for determining resonant frequencies for one-degree-of-freedom dynamic systems have been developed and the problem of its mathematical modeling has been solved. It should be noted that works [20,21] show that when the frequency of the excitation force interacts with the nonlinear characteristics of the dynamic system, it generates parametric vibration frequencies. Meanwhile, resonant frequencies are frequencies generated by subsystems and system parameters, namely: mass, stiffness characteristics of the system, degree of its nonlinearity and other properties. Therefore, it is necessary to distinguish clearly between resonant frequencies of the system and parametric vibration frequencies. Meanwhile, the results of the research work presented above do not distinguish and it is not clear what "resonant" frequencies we are talking about. The resonant frequencies of the system are not identical to the parametric frequencies and cannot be lumped into one place. Therefore, in the design stage of a dynamic system, it is very important to create a mathematical model that, by considering the resonant, parametric and external excitation frequencies of the system, would allow reducing its vibration level and ensure safe working conditions. Thus, the aim of the work is to analyze the one degree of freedom nonlinear dynamic systems vibrations depending on the excitation force frequency and its magnitude, to determine which system parameters and factors have a significant influence on vibration damping, and to show how to select properly the system parameters so that the vibration level is as low as possible and the system would work stably.
2. Investigation of the Influence of Excitation Force Frequency on System Vibration frequencies
The ability to determine the resonant and parametric vibration frequencies of a nonlinear dynamic system is not yet a sufficient condition for determining the influence of the frequency and size of the excitation force on the vibration intensity and frequency. The problem is that changing the excitation force frequency (angular velocity) and magnitude changes the spectral density of nonlinear dynamic system vibrations. It is said that the frequency of the maximum amplitude of vibrations in their spectral density is the frequency of the excitation force, which means the first harmonic of parametric vibrations. However, it is shown below in this paper that under certain operating conditions of a nonlinear dynamic system, the maximum vibration amplitude may sometimes correspond not to the excitation force frequency of the system, but to the frequency of the first harmonic or subharmonic. But its vibration magnitude is always among the first three largest vibration amplitudes of nonlinear dynamic systems. At higher frequencies, the amplitudes of system vibrations are significantly smaller (Table 1), so it is practically possible not to examine them. However, the order of variation of the frequencies of the largest first three amplitudes of the nonlinear dynamic system vibrations is unknown. Therefore, it is necessary to determine at least an approximate relationship between the frequency of the external excitation force 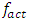 and the nonlinear dynamic system vibration spectrum at the three highest vibration amplitude frequencies.
and the nonlinear dynamic system vibration spectrum at the three highest vibration amplitude frequencies.Table 1. Vibration spectral density frequencies and amplitudes, n = 2
 |
| |
|
Thus, to consider the magnitude of the amplitude vibration as a function of the frequency of the external excitation force, the problem arises as to which amplitude 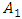 or
or 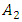 , or
, or 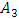 we want to determine as a function of
we want to determine as a function of 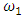 or
or 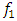 . After all, a nonlinear dynamic system vibrates more than one amplitude at different frequencies, just as only one amplitude linear system vibrates. Therefore, the latter problem is much more complex and it is not possible to express nonlinear dynamic system vibrations as a function of external excitation force frequency in single amplitude. Thus, in the first step of solving nonlinear dynamic system differential equations using MATLAB (and R K method), the dependence of the vibration amplitude
. After all, a nonlinear dynamic system vibrates more than one amplitude at different frequencies, just as only one amplitude linear system vibrates. Therefore, the latter problem is much more complex and it is not possible to express nonlinear dynamic system vibrations as a function of external excitation force frequency in single amplitude. Thus, in the first step of solving nonlinear dynamic system differential equations using MATLAB (and R K method), the dependence of the vibration amplitude 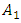 and the frequencies
and the frequencies 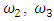 and
and 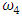 on the external excitation force frequency range
on the external excitation force frequency range 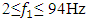 and the system nonlinearity range
and the system nonlinearity range 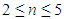 is determined. The calculations are performed with
is determined. The calculations are performed with 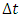 = 0.001 step values, the vibration calculation time t = 6.0 s, and the values of the basic vibration parameters are calculated in the vibration time interval 4 < t < 6 s.This is done in order to eliminate the vibration frequencies that are excited when the system begins to vibrate, that is, to eliminate part of the resonant frequencies of the system, the intensity of which is greatly reduced. The values of the main parameters of all studied dynamic systems are as follows: M = 5kg; F = 100000N; k = 100000N/m; c = 0.05;
= 0.001 step values, the vibration calculation time t = 6.0 s, and the values of the basic vibration parameters are calculated in the vibration time interval 4 < t < 6 s.This is done in order to eliminate the vibration frequencies that are excited when the system begins to vibrate, that is, to eliminate part of the resonant frequencies of the system, the intensity of which is greatly reduced. The values of the main parameters of all studied dynamic systems are as follows: M = 5kg; F = 100000N; k = 100000N/m; c = 0.05; 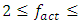
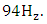 If the magnitude of any parameter will be changed, it will be indicated during the study. According to [7], when n = 2, the resonant frequencies of nonlinear dynamic systems are as follows:
If the magnitude of any parameter will be changed, it will be indicated during the study. According to [7], when n = 2, the resonant frequencies of nonlinear dynamic systems are as follows: 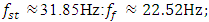
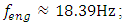
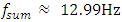 and when n = 3 then {39.30, 22.52, 15.92, 9.75} respectively. From the graph in Figure 1a, it can be seen that the degree of nonlinearity of the dynamic system in the value n and the excitation frequency
and when n = 3 then {39.30, 22.52, 15.92, 9.75} respectively. From the graph in Figure 1a, it can be seen that the degree of nonlinearity of the dynamic system in the value n and the excitation frequency 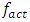 have a very significant effect on the level of system vibration and when
have a very significant effect on the level of system vibration and when 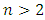 , at all values of the system excitation frequency
, at all values of the system excitation frequency 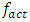 , the vibration level decreases significantly. Figure 1d shows how the excitation frequency vibration amplitude varies with the degree of system nonlinearity and the size of the stiffness coefficient k. When
, the vibration level decreases significantly. Figure 1d shows how the excitation frequency vibration amplitude varies with the degree of system nonlinearity and the size of the stiffness coefficient k. When 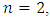 then the system's vibration level changes the most, as the system's excitation frequency increases to
then the system's vibration level changes the most, as the system's excitation frequency increases to 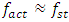 (Figure 1a). In order to better understand the increase in system vibrations level when
(Figure 1a). In order to better understand the increase in system vibrations level when 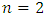 and 3, changing the
and 3, changing the 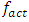 values, the graphs of the variation in the amplitude of their first harmonic vibrations are presented in Figure 1b and 1c. The latter results, when
values, the graphs of the variation in the amplitude of their first harmonic vibrations are presented in Figure 1b and 1c. The latter results, when 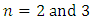 , are further detailed, as it can be seen from Figure 1a that at the indicated degree of system nonlinearity, the largest variation in the vibration level is observed, as the system excitation frequency changes. In this way, we can see from Figure 1b that the highest vibration level takes place when the system vibrates at the frequency
, are further detailed, as it can be seen from Figure 1a that at the indicated degree of system nonlinearity, the largest variation in the vibration level is observed, as the system excitation frequency changes. In this way, we can see from Figure 1b that the highest vibration level takes place when the system vibrates at the frequency 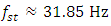 generated by the properties of the stiffness connection peculiarities and by further increasing the excitation frequency, the intensity of vibration decreases significantly. Meanwhile, when
generated by the properties of the stiffness connection peculiarities and by further increasing the excitation frequency, the intensity of vibration decreases significantly. Meanwhile, when 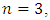 the vibration level of the system increases slightly at the resonance frequency
the vibration level of the system increases slightly at the resonance frequency 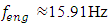 (Figure 2e) generated by the energy connection features, and as the excitation frequency
(Figure 2e) generated by the energy connection features, and as the excitation frequency 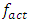 increases, the vibration amplitudes continuously decrease. There is also a slight increase in vibration amplitudes at the subharmonic frequency
increases, the vibration amplitudes continuously decrease. There is also a slight increase in vibration amplitudes at the subharmonic frequency 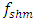 of the lowest resonant frequency (Figure1c). When
of the lowest resonant frequency (Figure1c). When 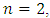 there is a slight increase in vibration amplitudes at resonant frequencies generated by the features of the system's force and energy connection, these are approximately at 22.5 and 18.5Hz (Figure 1a and b). At the latter frequencies, the peaks of the amplitudes are less visible. Thus, a very high level of vibrations is generated by the frequency of the stiffness connection properties and a high level of vibration in the latter frequency covers the amplitudes of vibrations of other frequencies. When
there is a slight increase in vibration amplitudes at resonant frequencies generated by the features of the system's force and energy connection, these are approximately at 22.5 and 18.5Hz (Figure 1a and b). At the latter frequencies, the peaks of the amplitudes are less visible. Thus, a very high level of vibrations is generated by the frequency of the stiffness connection properties and a high level of vibration in the latter frequency covers the amplitudes of vibrations of other frequencies. When 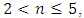 then due to high damping in the system, the vibration level decreases very strongly, as the excitation frequency of the system increases and resonance frequency vibrations are almost invisible (Figure 1a).
then due to high damping in the system, the vibration level decreases very strongly, as the excitation frequency of the system increases and resonance frequency vibrations are almost invisible (Figure 1a).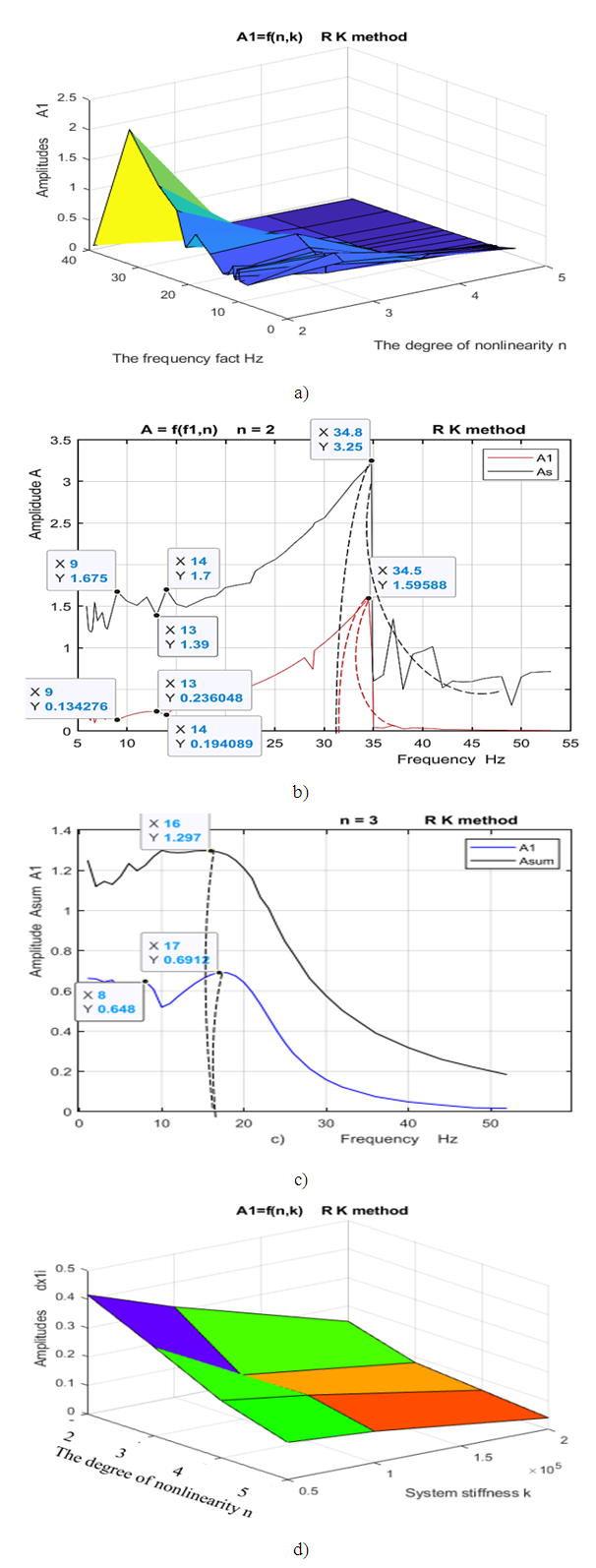 | Figure 1. The magnitude of the nonlinear dynamic system vibration amplitude as a function of its parameter values, F/k = 1.0 |
Therefore, when designing nonlinear dynamic systems, especially when n = 2, in order to avoid large vibrations in the system, it is necessary not to plan for them in the operating mode in the 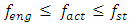 Hz frequency range. From the data in Table 1 and the vibration spectrum in Figure 2, it can be seen that the dynamic system has approximately 27Hz and other resonant frequencies that do not exist in the resonant frequencies of subsystems {31.85, 22.52, 18.34, 12.99}.
Hz frequency range. From the data in Table 1 and the vibration spectrum in Figure 2, it can be seen that the dynamic system has approximately 27Hz and other resonant frequencies that do not exist in the resonant frequencies of subsystems {31.85, 22.52, 18.34, 12.99}.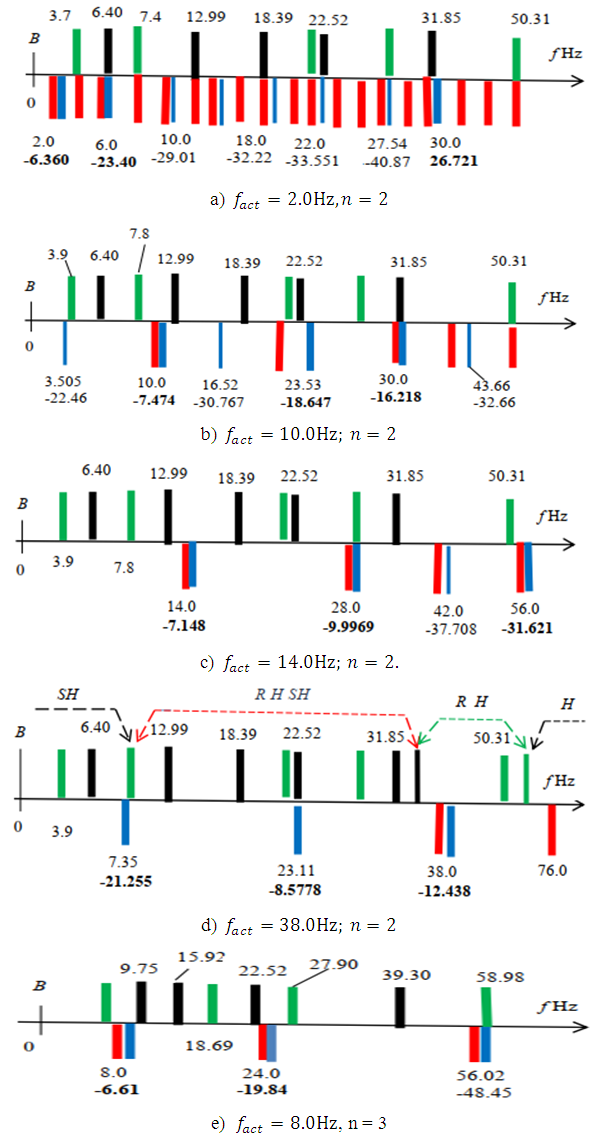 | Figure 2. Graphical interpretations of the vibrational spectral density of the spaces in the section in the B0f plane at different values of the excitation force frequency, F/k =1.0 |
It is assumed that the latter frequencies must be the frequencies of all dynamic systems. Therefore, the following system of differential equations is created and solved: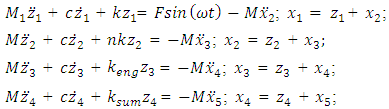 | (1) |
where M is mass of the system; c is coefficient of damping; k is coefficient of stiffness; n is exponent of 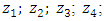
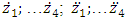 are velocity and acceleration; F is amplitude of excitation force;
are velocity and acceleration; F is amplitude of excitation force; 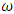 is angular frequency; t is time.After a simple transformation of the system of equations (1) we obtain:
is angular frequency; t is time.After a simple transformation of the system of equations (1) we obtain: 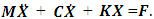 | (2) |
The damping coefficient and stiffness matrices are shown below: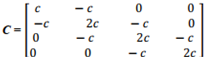 | (3) |
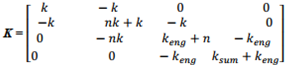 | (4) |
The basic diagonal of the M matrix, the first to fourth rows inclusive are 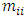 = M when i = 1; 2; ...; 4 In this way, the systems of left equations (2) are clear because the matrices of mass, damping coefficient (3) and stiffness (4) are known. How the matrix F is formed is studied in detail [21]. It is very important to make sure how much the resonant frequencies (eigenvalues) will change when the latter subsystems are combined into a common system. Thus, the system of equations (2) is transformed as follows:
= M when i = 1; 2; ...; 4 In this way, the systems of left equations (2) are clear because the matrices of mass, damping coefficient (3) and stiffness (4) are known. How the matrix F is formed is studied in detail [21]. It is very important to make sure how much the resonant frequencies (eigenvalues) will change when the latter subsystems are combined into a common system. Thus, the system of equations (2) is transformed as follows: 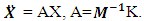 | (5) |
The system (5) can be solved by guessing the solution: 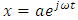 . By inserting
. By inserting 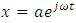 in to the system (5) and denoting
in to the system (5) and denoting 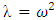 we obtain:
we obtain: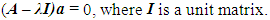 | (6) |
When n = 2 and 3, after solving the system of equations (6) in MATLAB, the following values of the eigenvalues of the whole dynamic system are obtained: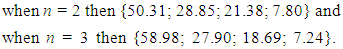 | (7) |
Thus, the results of the latter study show that the size of the approximate frequency 28.85Hz and other frequencies that do not correspond to the resonant frequencies of the subsystems are the resonant frequencies of the whole nonlinear dynamic system. In this way, depending on the size of the external excitation force frequency, the dynamic system itself chooses a different spectrum frequency band (see Table 1 and Figure 2 and 3). While investigating how the frequencies of the largest amplitudes of the nonlinear dynamic system depend on the excitation frequency, it was found that when 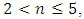 then the frequencies of the latter amplitudes change in the order (see Figure 2e):
then the frequencies of the latter amplitudes change in the order (see Figure 2e):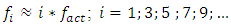 | (8) |
So, when 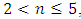 then the frequencies of vibration in a nonlinear dynamic system are identical to the frequencies of parametric vibration. However, at low system vibration frequencies, peaks in the vibration amplitudes may occur at low resonance frequencies or at subharmonic frequencies, but their magnitudes are small. When
then the frequencies of vibration in a nonlinear dynamic system are identical to the frequencies of parametric vibration. However, at low system vibration frequencies, peaks in the vibration amplitudes may occur at low resonance frequencies or at subharmonic frequencies, but their magnitudes are small. When 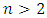 and is an even number, then its parametric vibration frequency amplitudes
and is an even number, then its parametric vibration frequency amplitudes 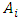 when i = 1, 3, 5, 7,… will be significantly higher than
when i = 1, 3, 5, 7,… will be significantly higher than 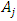 when j = 2,4,6... So, sometimes their vibrations in the spectral density can not always visible. Meanwhile, when
when j = 2,4,6... So, sometimes their vibrations in the spectral density can not always visible. Meanwhile, when 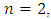 then the dependence of the frequency of the largest vibration amplitudes on the frequency of the system
then the dependence of the frequency of the largest vibration amplitudes on the frequency of the system 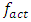 is complex and requires additional and careful research. Therefore, on the basis of the research results, it can be stated that in a vibrating nonlinear dynamic system with a constant value of its parameters, for each value of the excitation force there is a set of potential vibration frequencies (band), which is composed of subsystems and the resonant frequency of the system, their harmonic and subharmonic frequencies. In other words, in a nonlinear dynamic system there is a graded (discretized) space of potential vibration frequencies and a set of parametric forces acting on it, as well as sets of maximum amplitude vibrations and frequencies. The frequency space of potential vibrations, the set of parametric forces acting on it, and the set of system vibrations with the highest amplitude are shown in Figure 2. In Figure 2, resonance frequencies of the subsystem and the whole (general) system when the system is acted at the selected frequency
is complex and requires additional and careful research. Therefore, on the basis of the research results, it can be stated that in a vibrating nonlinear dynamic system with a constant value of its parameters, for each value of the excitation force there is a set of potential vibration frequencies (band), which is composed of subsystems and the resonant frequency of the system, their harmonic and subharmonic frequencies. In other words, in a nonlinear dynamic system there is a graded (discretized) space of potential vibration frequencies and a set of parametric forces acting on it, as well as sets of maximum amplitude vibrations and frequencies. The frequency space of potential vibrations, the set of parametric forces acting on it, and the set of system vibrations with the highest amplitude are shown in Figure 2. In Figure 2, resonance frequencies of the subsystem and the whole (general) system when the system is acted at the selected frequency 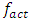 are shown above the line. Subsystem resonant frequencies are marked in bold black color and values of the whole (general) system resonant frequency – in bold green. In order not to darken the image too much, harmonic and subharmonic vibration frequencies are not shown above the line. At the bottom of the dash, there are the values of the excitation parametric forces and the system's largest vibration amplitudes. Parametric exciting forces are marked in red and values with the largest amplitudes in bold blue. From the vibration spectral density in Figure 2d, it can be seen that although the dynamic system is excited at the frequency of
are shown above the line. Subsystem resonant frequencies are marked in bold black color and values of the whole (general) system resonant frequency – in bold green. In order not to darken the image too much, harmonic and subharmonic vibration frequencies are not shown above the line. At the bottom of the dash, there are the values of the excitation parametric forces and the system's largest vibration amplitudes. Parametric exciting forces are marked in red and values with the largest amplitudes in bold blue. From the vibration spectral density in Figure 2d, it can be seen that although the dynamic system is excited at the frequency of 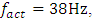 , the maximum vibration amplitude
, the maximum vibration amplitude 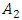 is excited at the frequency of 23.11Hz. Analyzing the set of frequencies (11), we will notice that the frequency of 7.35 Hz, which is the lowest resonant frequency of the whole system, is about 5 times repeated for the excitation frequency of 38 Hz and approximately three times repeated for the frequency of 22.5 Hz generated by the characteristic of the force connection. In this way, the system's acting frequencies do not have to be repeated for low-frequency resonant frequencies and subharmonic frequencies. In the Figure 2d, for clarity, the following frequency zones are shown additionally in the vibrational spectral density: SH - subharmonic; R SH H - resonance, harmonic and subharmonic; R H - resonance and harmonics, and H - harmonic frequencies of the approximate bands. It can also be seen from Figure 1 and Table 1 that when the excitation frequency is higher than the system resonant frequency
is excited at the frequency of 23.11Hz. Analyzing the set of frequencies (11), we will notice that the frequency of 7.35 Hz, which is the lowest resonant frequency of the whole system, is about 5 times repeated for the excitation frequency of 38 Hz and approximately three times repeated for the frequency of 22.5 Hz generated by the characteristic of the force connection. In this way, the system's acting frequencies do not have to be repeated for low-frequency resonant frequencies and subharmonic frequencies. In the Figure 2d, for clarity, the following frequency zones are shown additionally in the vibrational spectral density: SH - subharmonic; R SH H - resonance, harmonic and subharmonic; R H - resonance and harmonics, and H - harmonic frequencies of the approximate bands. It can also be seen from Figure 1 and Table 1 that when the excitation frequency is higher than the system resonant frequency 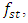 then the vibration amplitudes are small. The results of the research presented above show that by choosing properly the nonlinear dynamic parameters of the system and the excitation force frequency, it is possible to reduce the level of vibrations in the system.
then the vibration amplitudes are small. The results of the research presented above show that by choosing properly the nonlinear dynamic parameters of the system and the excitation force frequency, it is possible to reduce the level of vibrations in the system.
3. Investigation, Numerical Analysis and Discussion of the Influence of the Frequency and Magnitude of the Excitation Force on the Spectral Density of Vibrations
The research results show that when n = 2, then the frequencies with the highest amplitude vibrations for certain frequency groups are not generated according to the same law. In the frequency band of the spectral density of the vibration, 6 zones can be roughly distinguished according to frequencies: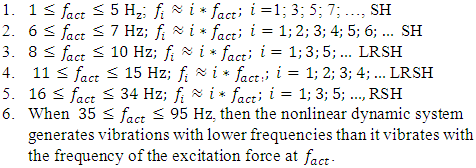 | (9) |
Where SH is low frequency subharmonics zone; LRSH is zone of low resonance and subharmonic frequencies; RSH is frequency zone of resonances and subharmonics. It is necessary to pay attention to the fact that when the excitation frequency 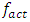 is higher than the frequency
is higher than the frequency 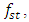 then the vibrations in the spectrum appear at a lower frequency than
then the vibrations in the spectrum appear at a lower frequency than 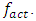 Therefore, when choosing the system excitation force frequency, it is necessary to consider cases of possible resonance in the designed system. Sometimes, when
Therefore, when choosing the system excitation force frequency, it is necessary to consider cases of possible resonance in the designed system. Sometimes, when 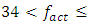
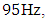 the vibration amplitude
the vibration amplitude 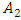 can be higher than
can be higher than 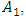 generated by vibrating the system at
generated by vibrating the system at 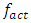 frequency (see Figure 2 and 3). However, when the excitation frequency
frequency (see Figure 2 and 3). However, when the excitation frequency 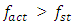 and the magnitude of the excitation force does not change (constant), then the system has a very low vibration level (see Figure 1). While analyzing the results of the study of the influence of the excitation force frequency on the vibration frequencies of the system, it was found that: – when the excitation frequency of the system is higher than the frequency
and the magnitude of the excitation force does not change (constant), then the system has a very low vibration level (see Figure 1). While analyzing the results of the study of the influence of the excitation force frequency on the vibration frequencies of the system, it was found that: – when the excitation frequency of the system is higher than the frequency 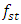 created by the characteristics of the stiffness connection, that is, when
created by the characteristics of the stiffness connection, that is, when 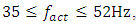 then the dynamic system can vibrate at some subsystem, the whole system and their subharmonics at resonant frequencies (see Fig. 2c), and there may be more than two of them;– when the dynamic system is vibrated with a frequency of
then the dynamic system can vibrate at some subsystem, the whole system and their subharmonics at resonant frequencies (see Fig. 2c), and there may be more than two of them;– when the dynamic system is vibrated with a frequency of 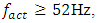 then very low-frequency vibrations occur in it, the frequency of which is the subharmonic frequency
then very low-frequency vibrations occur in it, the frequency of which is the subharmonic frequency 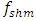 of the lowest resonant frequency of the system. And the dynamic system vibrates with only two frequencies, the excitation frequency and one of the system's low resonant frequencies or some subharmonic frequencies, which repeat the excitation frequency (see Table 1 and Figure 2 and 3). Also, from the result of Table 1 and Figure 3, it can be seen that when the nonlinear dynamic system is excited with the frequency
of the lowest resonant frequency of the system. And the dynamic system vibrates with only two frequencies, the excitation frequency and one of the system's low resonant frequencies or some subharmonic frequencies, which repeat the excitation frequency (see Table 1 and Figure 2 and 3). Also, from the result of Table 1 and Figure 3, it can be seen that when the nonlinear dynamic system is excited with the frequency  then it generates vibrations with a frequency of approximately 20Hz, with amplitude higher than the excitation frequency of 40 Hz. In this way, it seems that the system is excited at a frequency of 20Hz, because the vibration level is the highest at the latter frequency, and then the vibration frequencies of the system seem to change in this order:
then it generates vibrations with a frequency of approximately 20Hz, with amplitude higher than the excitation frequency of 40 Hz. In this way, it seems that the system is excited at a frequency of 20Hz, because the vibration level is the highest at the latter frequency, and then the vibration frequencies of the system seem to change in this order:  i = 1; 2; 3; 4… (Figure 3a). In this way, the statement in the work [20] is confirmed, that in a nonlinear dynamic system, high-amplitude vibrations generate acting forces. The spectra of the simplified spatial spectral density shown in Figure 2 and 3 have been examined above, in the following material we will call the frequency band of the spectral density, which is generated for the system excitation frequency
i = 1; 2; 3; 4… (Figure 3a). In this way, the statement in the work [20] is confirmed, that in a nonlinear dynamic system, high-amplitude vibrations generate acting forces. The spectra of the simplified spatial spectral density shown in Figure 2 and 3 have been examined above, in the following material we will call the frequency band of the spectral density, which is generated for the system excitation frequency  of a certain size.
of a certain size.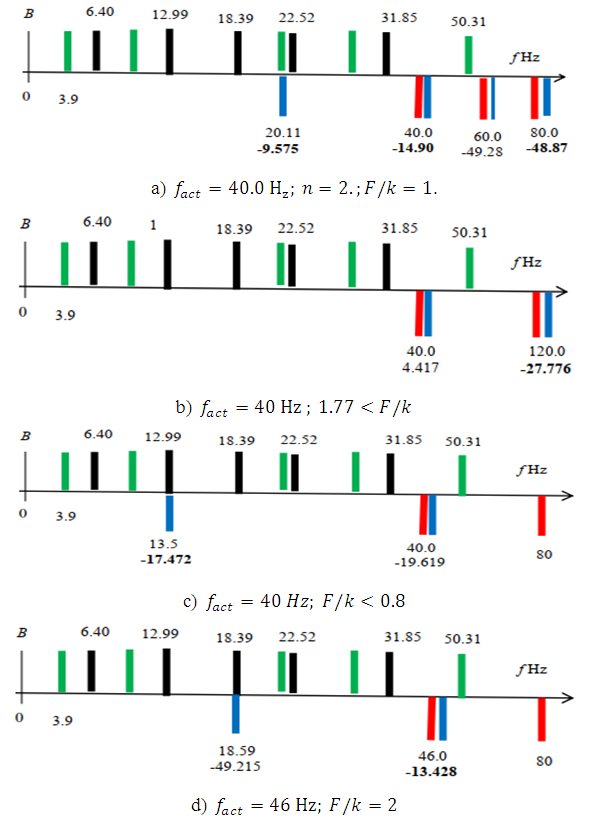 | Figure 3. Sections of the spectral density of spatial vibrations in the B0f plane at different values of the excitation force |
The results of recent research and those presented in Figure 3 shows that when the level of vibration intensity changes in the spectral density as the force magnitude changes and the vibrational frequency spectrum also changes approximately in the following order: – when F/k < 0.8 then vibrations at resonant frequencies of the system, their harmonic and subharmonic frequencies occur between the parametric vibration frequencies. When 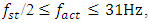 then the maximum vibration frequency of the system varies approximately according to the law:
then the maximum vibration frequency of the system varies approximately according to the law: 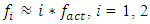 and when
and when 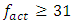 then
then 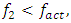 i.e. vibrations are generated at subharmonic frequencies that are multiples of the excitation frequency. In addition, it has been determined that in the considered case the resonance frequencies of the general dynamic system, their subharmonic and harmonic frequencies are more visible in the vibration spectral density, and the maximum vibration size is approximately reached at the frequency of 28 - 29 Hz, i.e. at the third largest resonant frequency of the overall system.– when 0.8 < F/k < 1.77, then the frequencies of the dynamic system vibrations with the largest amplitudes will change approximately according to the specified laws (9);– when F/k >1.77 and
i.e. vibrations are generated at subharmonic frequencies that are multiples of the excitation frequency. In addition, it has been determined that in the considered case the resonance frequencies of the general dynamic system, their subharmonic and harmonic frequencies are more visible in the vibration spectral density, and the maximum vibration size is approximately reached at the frequency of 28 - 29 Hz, i.e. at the third largest resonant frequency of the overall system.– when 0.8 < F/k < 1.77, then the frequencies of the dynamic system vibrations with the largest amplitudes will change approximately according to the specified laws (9);– when F/k >1.77 and 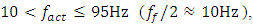 then the dynamic system vibrates at approximately the following frequencies:
then the dynamic system vibrates at approximately the following frequencies: 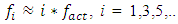 When the system's excitation frequency
When the system's excitation frequency 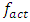 coincides with or has multiple lower resonance frequencies, its subharmonic and harmonic frequencies, the system vibrates at the system's lowest resonant frequency or subharmonic frequency. However, at higher frequencies, when
coincides with or has multiple lower resonance frequencies, its subharmonic and harmonic frequencies, the system vibrates at the system's lowest resonant frequency or subharmonic frequency. However, at higher frequencies, when 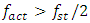 , the amplitudes of the dynamic system's vibrations decrease significantly as the values of i increase, and the vibration amplitudes are significant only when i = 1,3 or even when i = 1.In this way, it is determined that when a low-frequency subharmonic or a lower resonance frequency is a multiple of the excitation frequency
, the amplitudes of the dynamic system's vibrations decrease significantly as the values of i increase, and the vibration amplitudes are significant only when i = 1,3 or even when i = 1.In this way, it is determined that when a low-frequency subharmonic or a lower resonance frequency is a multiple of the excitation frequency 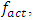 and
and 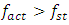 , its vibration level is higher than the size of the vibration generated by the
, its vibration level is higher than the size of the vibration generated by the 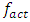 frequency (see Figure 3a and 3c). It was also found that the response of the nonlinear dynamic system to the magnitude of the excitation force is twofold: when F/k > 0.8, then the main resonance in the system corresponds to the frequency generated by the characteristics of the stiffness connection (see Fig. 1a) and when F/k < 0.8, then it corresponds to the third resonant frequency of the whole system in terms of magnitude, which is in the range of 28 - 29Hz. In this way, according to recent research results, when the frequency of excitation is in the interval
frequency (see Figure 3a and 3c). It was also found that the response of the nonlinear dynamic system to the magnitude of the excitation force is twofold: when F/k > 0.8, then the main resonance in the system corresponds to the frequency generated by the characteristics of the stiffness connection (see Fig. 1a) and when F/k < 0.8, then it corresponds to the third resonant frequency of the whole system in terms of magnitude, which is in the range of 28 - 29Hz. In this way, according to recent research results, when the frequency of excitation is in the interval 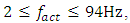 it is determined:– resonant, harmonic and subharmonic frequencies of constant size space, and two-dimensional arrays of dynamic systems with the largest vibration amplitudes and frequencies in each section of the plane B0f (see Figure 2 and 3); – three-dimensional spatial array of vibrational spectral density SD, in which the values of the vibration amplitude, their frequency and the system's excitation frequency will vary. It means that the vibration spectral density space SD can be defined (described) by a three-dimensional matrix (array), which is specified using three indices: block size
it is determined:– resonant, harmonic and subharmonic frequencies of constant size space, and two-dimensional arrays of dynamic systems with the largest vibration amplitudes and frequencies in each section of the plane B0f (see Figure 2 and 3); – three-dimensional spatial array of vibrational spectral density SD, in which the values of the vibration amplitude, their frequency and the system's excitation frequency will vary. It means that the vibration spectral density space SD can be defined (described) by a three-dimensional matrix (array), which is specified using three indices: block size 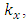 row size
row size 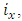 and column size
and column size 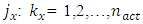 – the number of excitation force frequencies
– the number of excitation force frequencies 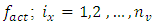 – the number of vibration frequencies of a nonlinear dynamic system
– the number of vibration frequencies of a nonlinear dynamic system 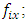
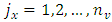 – the number of vibration amplitudes of a nonlinear dynamic system. In this way, it is shown that for all values of the excitation frequency
– the number of vibration amplitudes of a nonlinear dynamic system. In this way, it is shown that for all values of the excitation frequency 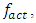 the upper part of the graph in Figures 2 and 3 is an invariant (constant) part and includes the resonant frequencies of the system subsystems and the whole system, their subharmonic and harmonic frequencies. The changing part of the spectral density space will be only a part (a set) of the frequencies generated by the system and a set of the maximum amplitudes of the system's vibrations. In this way, the spectral density of the nonlinear dynamic system in the potential frequency space is determined according to the mathematical apparatus presented in previous works [20,21] and their magnitudes are described by the following sets:
the upper part of the graph in Figures 2 and 3 is an invariant (constant) part and includes the resonant frequencies of the system subsystems and the whole system, their subharmonic and harmonic frequencies. The changing part of the spectral density space will be only a part (a set) of the frequencies generated by the system and a set of the maximum amplitudes of the system's vibrations. In this way, the spectral density of the nonlinear dynamic system in the potential frequency space is determined according to the mathematical apparatus presented in previous works [20,21] and their magnitudes are described by the following sets: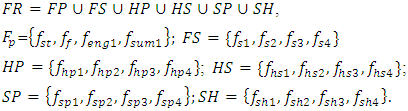 | (10) |
where 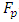 – set of resonant frequencies of subsets system; FS – subset of resonant frequencies of system; HP – subset of resonant frequency harmonics of subsystem; HS – subset of resonant frequency harmonics of system; SP – subset of resonant frequency subharmonics of subsystem; SH – subset of resonant frequency harmonics of system. For example, in the considered case where n = 2, the set of FR will have approximately the following frequency values:
– set of resonant frequencies of subsets system; FS – subset of resonant frequencies of system; HP – subset of resonant frequency harmonics of subsystem; HS – subset of resonant frequency harmonics of system; SP – subset of resonant frequency subharmonics of subsystem; SH – subset of resonant frequency harmonics of system. For example, in the considered case where n = 2, the set of FR will have approximately the following frequency values: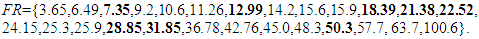 | (11) |
In fact, the values of the FR set of frequencies must be slightly lower, because the effect of damping forces was not evaluated when determining their values. And when examining the dynamic vibration spectra of the system, slightly lower values than the calculated values were seen. The excitation force frequency in a nonlinear dynamic system generates a set of parametric forces that can be described as follows: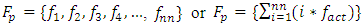 | (12) |
where i = 1,2,3,4,...,nn, for even n; and i= 1, 3, 5,…nn, for odd n [7].For each excitation force 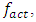 the set of parametric excitation force sizes
the set of parametric excitation force sizes 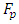 will be different. In this way, the parametric forces of the set
will be different. In this way, the parametric forces of the set 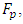 in interaction with the dynamic properties of the system and the frequency set FR of the spectral density space, for each excitation force
in interaction with the dynamic properties of the system and the frequency set FR of the spectral density space, for each excitation force 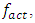 will generate the vibrational spectral density of the latter space in the plane B0f (see Figure 2 and 3). In fact, for each excitation force, the vibrations of the system will be described by a two-dimensional array, one row of which will contain the maximum vibration amplitudes, and the second row will contain the vibration frequencies of the system, corresponding to the order of presentation of the vibration amplitudes:
will generate the vibrational spectral density of the latter space in the plane B0f (see Figure 2 and 3). In fact, for each excitation force, the vibrations of the system will be described by a two-dimensional array, one row of which will contain the maximum vibration amplitudes, and the second row will contain the vibration frequencies of the system, corresponding to the order of presentation of the vibration amplitudes: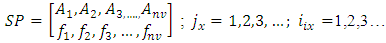 | (13) |
where 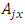 – amplitudes of nonlinear dynamic system vibrations;
– amplitudes of nonlinear dynamic system vibrations; 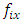 – vibration frequencies of a nonlinear dynamic system.To determine the vibration frequencies of nonlinear dynamic systems, it is convenient to use the methodology set out above (see Figure 2 and 3), which allows creating a potential spectral density frequency band for each excitation force and using the determined system characteristics (features) (8); (9); (10); (13) to create an approximate one-dimensional array of vibration frequencies
– vibration frequencies of a nonlinear dynamic system.To determine the vibration frequencies of nonlinear dynamic systems, it is convenient to use the methodology set out above (see Figure 2 and 3), which allows creating a potential spectral density frequency band for each excitation force and using the determined system characteristics (features) (8); (9); (10); (13) to create an approximate one-dimensional array of vibration frequencies 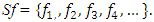 When the vibration frequencies of nonlinear dynamical systems are determined, then the number of unknowns is reduced by two times and the number of unknowns in differential equations will be equal to the number of equations. In order to clarify the physics of nonlinear dynamic system vibrations and to show the suitability of the considered method for vibration analysis and the possibility of reducing vibrations in a nonlinear dynamic system, the acting frequency of 40Hz was chosen not by chance. The latter frequency 40Hz is a harmonic of the frequency
When the vibration frequencies of nonlinear dynamical systems are determined, then the number of unknowns is reduced by two times and the number of unknowns in differential equations will be equal to the number of equations. In order to clarify the physics of nonlinear dynamic system vibrations and to show the suitability of the considered method for vibration analysis and the possibility of reducing vibrations in a nonlinear dynamic system, the acting frequency of 40Hz was chosen not by chance. The latter frequency 40Hz is a harmonic of the frequency 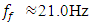 generated by the peculiarities of the system's force connections. However, let's examine the vibrations of the dynamic system of the latter case and the stability of its operation. We will perform the study of nonlinear dynamic system vibration magnitude dependences on the excitation frequency and force size with the help of MATLAB. For example, when the magnitude of the excitation force is F=100000N and the system vibrates at 40Hz. it is
generated by the peculiarities of the system's force connections. However, let's examine the vibrations of the dynamic system of the latter case and the stability of its operation. We will perform the study of nonlinear dynamic system vibration magnitude dependences on the excitation frequency and force size with the help of MATLAB. For example, when the magnitude of the excitation force is F=100000N and the system vibrates at 40Hz. it is 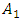 = -14.304(40Hz));
= -14.304(40Hz)); 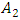 = -9.749(20.09Hz) and
= -9.749(20.09Hz) and 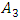 = -48.872 (80.0Hz), and when the system is vibrated with F=200000N force, then at the same frequency
= -48.872 (80.0Hz), and when the system is vibrated with F=200000N force, then at the same frequency 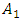 = 4.514(40Hz);
= 4.514(40Hz); 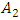 = -27.552(120Hz). It can be seen from the latest data that when the force is doubled, the amplitude of the largest vibrations has increased
= -27.552(120Hz). It can be seen from the latest data that when the force is doubled, the amplitude of the largest vibrations has increased 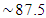 times:
times: 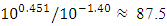 . When the acting frequency is not 40Hz, but
. When the acting frequency is not 40Hz, but 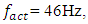 and F= 200000N then the vibration amplitudes of the latter system are greatly reduced, compared to the frequency when the system vibrates
and F= 200000N then the vibration amplitudes of the latter system are greatly reduced, compared to the frequency when the system vibrates 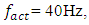 at F=200000N:
at F=200000N: 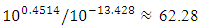 times and will be of small magnitude. The latter frequency was chosen because it is between 40Hz - the harmonic frequency and 50.31Hz - the resonant frequency of the system. The vibrations at the resonant frequency of 18.59Hz (see Figure 3d), is very small. In this way, when
times and will be of small magnitude. The latter frequency was chosen because it is between 40Hz - the harmonic frequency and 50.31Hz - the resonant frequency of the system. The vibrations at the resonant frequency of 18.59Hz (see Figure 3d), is very small. In this way, when 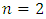 the results of the last calculation show that when the excitation frequency is higher than the resonance frequency of the subsystem, generated by the features of the stiffness connection and F/k > 0.8, the level of nonlinear dynamic vibrations of the system will be minimal and the system will work stably only when the constancy of the excitation frequency and its force magnitude is guaranteed. Even variable nonlinear dynamic load of the system (variable internal friction size of the system and disturbances of other stimuli) can cause changes in the magnitude of force F and, as a result, non-stable working conditions can be created for the system. If the latter requirements are not ensured, the dynamic vibration level of the system may change periodically even several tens of times, in addition, a jumpy (pulsating) working mode will be felt and the system will work unstable. The significance of the spatial frequency band of vibration spectral density in the study and design of new systems is shown. When the degree of nonlinearity of the dynamic system is within the limits of
the results of the last calculation show that when the excitation frequency is higher than the resonance frequency of the subsystem, generated by the features of the stiffness connection and F/k > 0.8, the level of nonlinear dynamic vibrations of the system will be minimal and the system will work stably only when the constancy of the excitation frequency and its force magnitude is guaranteed. Even variable nonlinear dynamic load of the system (variable internal friction size of the system and disturbances of other stimuli) can cause changes in the magnitude of force F and, as a result, non-stable working conditions can be created for the system. If the latter requirements are not ensured, the dynamic vibration level of the system may change periodically even several tens of times, in addition, a jumpy (pulsating) working mode will be felt and the system will work unstable. The significance of the spatial frequency band of vibration spectral density in the study and design of new systems is shown. When the degree of nonlinearity of the dynamic system is within the limits of 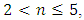 then when the magnitude of the excitation force changes in the interval
then when the magnitude of the excitation force changes in the interval 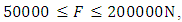 only the magnitude of the vibrations changes, but the frequency spectrum is constant. So, when n = 2, the possibilities to significantly reduce the level of vibration in the system are explained and demonstrated, the processes taking place in it are clarified. In this way, the research results show that when
only the magnitude of the vibrations changes, but the frequency spectrum is constant. So, when n = 2, the possibilities to significantly reduce the level of vibration in the system are explained and demonstrated, the processes taking place in it are clarified. In this way, the research results show that when 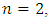 then if the system does not have any restrictions on working modes, then the lower vibration level in the nonlinear dynamic system will take place if the excitation frequency satisfies the condition:
then if the system does not have any restrictions on working modes, then the lower vibration level in the nonlinear dynamic system will take place if the excitation frequency satisfies the condition: 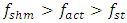 , and when
, and when 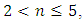 then it should be:
then it should be: 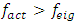 . In both of the latter cases, the excitation frequency must not coincide with or be close to, or a multiple of, the resonant frequencies of the nonlinear dynamic system, its harmonic and subharmonic frequencies. In this way, the research results show that there are three kinds (types) of vibrations in the nonlinear dynamic system: system resonance, parametric and systems. Therefore, knowing the latter types of frequencies of the nonlinear dynamic system and using the spectral density frequency band method discussed above, it is possible to choose the appropriate excitation frequency of the system and significantly reduce its vibration level. And if it is not possible to change the excitation frequency of the system, then it is possible to change the main parameters of the system and in this way create conditions so that excitation frequency does not coincide with its resonant frequencies.
. In both of the latter cases, the excitation frequency must not coincide with or be close to, or a multiple of, the resonant frequencies of the nonlinear dynamic system, its harmonic and subharmonic frequencies. In this way, the research results show that there are three kinds (types) of vibrations in the nonlinear dynamic system: system resonance, parametric and systems. Therefore, knowing the latter types of frequencies of the nonlinear dynamic system and using the spectral density frequency band method discussed above, it is possible to choose the appropriate excitation frequency of the system and significantly reduce its vibration level. And if it is not possible to change the excitation frequency of the system, then it is possible to change the main parameters of the system and in this way create conditions so that excitation frequency does not coincide with its resonant frequencies.
4. Conclusions
Analytical results The results of the analytical study prove that:1. It is shown that in a nonlinear dynamic system, the spectral density space is graded (discretized) according to resonant frequencies, their harmonic and subharmonic frequencies, and is invariant (constant) for selected values of the main parameters of the system. The frequency spectrum of the latter space does not depend on the excitation frequency; 2. The spectral density space frequency band method is presented for studying the frequencies and vibration intensities of vibrational dynamic systems;3. It was determined that there are three types of frequencies in a nonlinear dynamic system: resonance frequencies of system and subsystems, parametric vibration frequencies and dynamic system vibration frequencies. The non-identity of nonlinear dynamic systems with resonance frequency and parametric vibration frequency is highlighted. The results of numerical calculations The results of numerical calculations allow us to prove that:1. When the degree of nonlinearity of a nonlinear dynamic system is greater than 2, then its vibration frequency changes according to the order of the parametric frequency of the system. When the magnitude of the excitation force changes, then only the magnitude of the system vibration changes, but their frequency spectrum does not change. 2. When the degree of nonlinearity of the nonlinear dynamic system is n = 2, then:– depending on the excitation frequency and its force magnitude, the frequencies and sizes of the vibrations in the spectral density will vary;– the level of vibration in a nonlinear dynamic system increases the most when the excitation frequency is equal to the resonant frequency generated by the stiffness connection peculiarities of the nonlinear dynamic system, and with a smaller excitation force - the maximum vibration size is approximately reached at the third largest resonant frequency of the overall system.– it is shown that when the excitation force frequency is higher than the resonant frequency of the subsystems, generated by the peculiarities of its stiffness connection, then by properly selecting its frequency and other parameters, without using an additional damper, the vibration level can be reduced by several times; – it has been determined that if the frequency of the excitation force or its magnitude changes, conditions are created in the system for a jump in the size of the vibration and a change in its frequency spectrum, and the vibration level can increase several tens of times;– it was determined that when the excitation frequency is higher than the frequency generated by the characteristics of the stiffness connection, the amplitude of its frequency vibrations can be smaller than the amplitude of the vibrations of a lower frequency.
References
| [1] | S. L. Han1 and Takeshi Kinoshita1, 2012. Nonlinear damping identification in nonlinear dynamic system based on stochastic inverse approach. Matthematical problems in engineering, Volume 10, pp.65-72. |
| [2] | Xuechuan W., Xiaokui Y., Honghua D., Haoyang F., Satya N. Atluri. 2022. Computational Methods for Nonlinear Dynamical Systems. Theory and Applications in Aerospace Engineering1st Edition p. 240. |
| [3] | Ca Zhang, ... Zongun C. 2022. Nonlinear vibration. Machinery Dynamics. p. 474. |
| [4] | Vincent U. E., Mclinton P.V.E., Khovan I. A., Rajasekar S. 2021. Vibrational and Stochastic resonances in driven nonlinear systems. Mathematical, Physical and Engineering sciences, pp 12. |
| [5] | Willians R. A. Gody, Markelo A. Trinda de, 2020. Disign and analysis of a geometrically nonlnear dynamic vibration absorber. ASME Journal of computational and nonlinear dynamics. Volume 15(8), p. 9. |
| [6] | Peng, Z.K., Lang, Z.Q. and Billings, S.A. 2006 Resonances and resonant frequencies for a class of nonlinear systems. Research Report. ACSE Research Report no. 920. Automatic Control and Systems Engineering, University of Sheffield, p 30. |
| [7] | Luo. J. Liu X. 2015. An approximate response of the large system with local cubic nonlinearities subjected to harmonic exitation. Engineering Rewiew, 34, 1, pp. 49-59. |
| [8] | Richard H. Rand, 2005 Lecture Nots on Nonlinear Vibrations. Ithaca NY 14853, rhr2@cornell.edu, p.111. http://www.tam.cornell.edu/randdors/. |
| [9] | Lamarque C.H. 1991. Analysis of non-linear dynamical systems by the normal form theory. Journal of Sound and Vibration Volume 149, Issue 3, 22, pp. 429-459. |
| [10] | Bguet S. Prabel B. Dufour R. 2017. Bifurcation tracking by Harmonic Balance Method for performance tuning of nonlinear dynamical systems. Mechanical Systems and Signal Processing Volume 88, 1, pp. 445-461. |
| [11] | Narayanan S., Sekar P., 1998. A frequency domain based numerical – analytical method for non – linear dynamical systems. Journal of Sound and Vibration. Volume 211, Issue 3, 2, pp. 409-424. |
| [12] | Yu S. D. 2012. An efficient computational method for vibration analysis of unsymmetrical piecewise-linear dynamical systems with multiple degrees of freedom. Nonlinear Dynamics, volume 71, pp. 493 – 504. |
| [13] | Abdelbaki A., R., Paidoussis M. P. Mirsa A., K. 2019. A nonlinear model for a hanging tubular cantilever simultaneously subjected to internal and confined external axial flows. Journal of Sound and Vibration, Volume 449, pp. 349 – 367. |
| [14] | S. J. Elliot, M. Gedrachi Tehrani and R. S. Langley, 2014. Nonlinear damping and qasi-linear modrling. Mathematical, phisical and engineering sciences. 2015. https://doi.Org/10.1098/rsta.2014.0402. |
| [15] | H. S. Bauamy, A. T. El – Saved, F. T. EL – Bohrawy, A. M. Salem, 2023. Safety of a continuous spinning Shaft’s structure from nonlinear vibration with NIPPF. Alexandria Engineering Journal. Volume 67, pp. 193 – 207. https//doi.org/10.1016/j.aej.2022.12050. |
| [16] | J. M. Londono, Simon A. Neild, 2015. Indefication of bacbone curves of nonlinear systems from resonance decay responses. Volueme 348, pp. 224 – 238. |
| [17] | M. Ei SSO, W. A. A., El – Ganaini, Y. S. Hamed, 2005. Saturation, stability and resonance of non-linear systems. Statistical Mechaninics and its applications. Volume 356, Issues 2-4, PP. 341– 358. |
| [18] | Wen – Ming Zhang, Guang Meng, 2007. Nonlinear dynamic analysis of electrostatically actuated resonant MEMS sensors under parametric excitation. IEEE Sensors Journal, Volume 7. Issue 3, pp. 370 – 380. DOI: 10.1109/JSEN.2006.890158. |
| [19] | U. E. Vincent, P. V. E. McClinton, I. A. Khovanov and S. Rojasekar, 2021. Vibrational and stochastic resonances in driven nonlinear systems. Mathematical, Phisical and Engineering Sciencies. Philosofical Transection A, p. 9. DOI. org/10.1098/rasta.2020.0226. |
| [20] | Mariunas M. 2020. Methods for determinig resonant and parametric excitation frequencies of nonlinear dynamic systems. American Journal of Computational and Applied Mthematcs, 10(1), pp. 6-14. DOI: 10.5923/j.ajcam.2201001.02. |
| [21] | Mariunas M. 2021. Method for determining a research model of nonliniear two degre of freedom dynamic system. American Journal of Computational and Applied Mathematics, 11(2); 1-11. DOI: 10.5923/j.ajcam.20211102.01. |



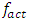 and the nonlinear dynamic system vibration spectrum at the three highest vibration amplitude frequencies.
and the nonlinear dynamic system vibration spectrum at the three highest vibration amplitude frequencies.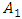 or
or 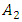 , or
, or 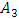 we want to determine as a function of
we want to determine as a function of 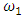 or
or 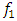 . After all, a nonlinear dynamic system vibrates more than one amplitude at different frequencies, just as only one amplitude linear system vibrates. Therefore, the latter problem is much more complex and it is not possible to express nonlinear dynamic system vibrations as a function of external excitation force frequency in single amplitude. Thus, in the first step of solving nonlinear dynamic system differential equations using MATLAB (and R K method), the dependence of the vibration amplitude
. After all, a nonlinear dynamic system vibrates more than one amplitude at different frequencies, just as only one amplitude linear system vibrates. Therefore, the latter problem is much more complex and it is not possible to express nonlinear dynamic system vibrations as a function of external excitation force frequency in single amplitude. Thus, in the first step of solving nonlinear dynamic system differential equations using MATLAB (and R K method), the dependence of the vibration amplitude 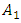 and the frequencies
and the frequencies 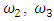 and
and 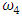 on the external excitation force frequency range
on the external excitation force frequency range 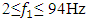 and the system nonlinearity range
and the system nonlinearity range 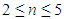 is determined. The calculations are performed with
is determined. The calculations are performed with 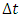 = 0.001 step values, the vibration calculation time t = 6.0 s, and the values of the basic vibration parameters are calculated in the vibration time interval 4 < t < 6 s.This is done in order to eliminate the vibration frequencies that are excited when the system begins to vibrate, that is, to eliminate part of the resonant frequencies of the system, the intensity of which is greatly reduced. The values of the main parameters of all studied dynamic systems are as follows: M = 5kg; F = 100000N; k = 100000N/m; c = 0.05;
= 0.001 step values, the vibration calculation time t = 6.0 s, and the values of the basic vibration parameters are calculated in the vibration time interval 4 < t < 6 s.This is done in order to eliminate the vibration frequencies that are excited when the system begins to vibrate, that is, to eliminate part of the resonant frequencies of the system, the intensity of which is greatly reduced. The values of the main parameters of all studied dynamic systems are as follows: M = 5kg; F = 100000N; k = 100000N/m; c = 0.05; 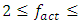
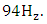 If the magnitude of any parameter will be changed, it will be indicated during the study. According to [7], when n = 2, the resonant frequencies of nonlinear dynamic systems are as follows:
If the magnitude of any parameter will be changed, it will be indicated during the study. According to [7], when n = 2, the resonant frequencies of nonlinear dynamic systems are as follows: 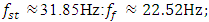
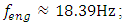
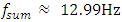 and when n = 3 then {39.30, 22.52, 15.92, 9.75} respectively. From the graph in Figure 1a, it can be seen that the degree of nonlinearity of the dynamic system in the value n and the excitation frequency
and when n = 3 then {39.30, 22.52, 15.92, 9.75} respectively. From the graph in Figure 1a, it can be seen that the degree of nonlinearity of the dynamic system in the value n and the excitation frequency 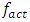 have a very significant effect on the level of system vibration and when
have a very significant effect on the level of system vibration and when 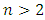 , at all values of the system excitation frequency
, at all values of the system excitation frequency 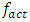 , the vibration level decreases significantly. Figure 1d shows how the excitation frequency vibration amplitude varies with the degree of system nonlinearity and the size of the stiffness coefficient k. When
, the vibration level decreases significantly. Figure 1d shows how the excitation frequency vibration amplitude varies with the degree of system nonlinearity and the size of the stiffness coefficient k. When 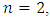 then the system's vibration level changes the most, as the system's excitation frequency increases to
then the system's vibration level changes the most, as the system's excitation frequency increases to 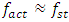 (Figure 1a). In order to better understand the increase in system vibrations level when
(Figure 1a). In order to better understand the increase in system vibrations level when 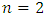 and 3, changing the
and 3, changing the 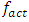 values, the graphs of the variation in the amplitude of their first harmonic vibrations are presented in Figure 1b and 1c. The latter results, when
values, the graphs of the variation in the amplitude of their first harmonic vibrations are presented in Figure 1b and 1c. The latter results, when 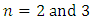 , are further detailed, as it can be seen from Figure 1a that at the indicated degree of system nonlinearity, the largest variation in the vibration level is observed, as the system excitation frequency changes. In this way, we can see from Figure 1b that the highest vibration level takes place when the system vibrates at the frequency
, are further detailed, as it can be seen from Figure 1a that at the indicated degree of system nonlinearity, the largest variation in the vibration level is observed, as the system excitation frequency changes. In this way, we can see from Figure 1b that the highest vibration level takes place when the system vibrates at the frequency 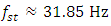 generated by the properties of the stiffness connection peculiarities and by further increasing the excitation frequency, the intensity of vibration decreases significantly. Meanwhile, when
generated by the properties of the stiffness connection peculiarities and by further increasing the excitation frequency, the intensity of vibration decreases significantly. Meanwhile, when 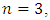 the vibration level of the system increases slightly at the resonance frequency
the vibration level of the system increases slightly at the resonance frequency 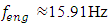 (Figure 2e) generated by the energy connection features, and as the excitation frequency
(Figure 2e) generated by the energy connection features, and as the excitation frequency 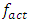 increases, the vibration amplitudes continuously decrease. There is also a slight increase in vibration amplitudes at the subharmonic frequency
increases, the vibration amplitudes continuously decrease. There is also a slight increase in vibration amplitudes at the subharmonic frequency 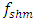 of the lowest resonant frequency (Figure1c). When
of the lowest resonant frequency (Figure1c). When 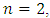 there is a slight increase in vibration amplitudes at resonant frequencies generated by the features of the system's force and energy connection, these are approximately at 22.5 and 18.5Hz (Figure 1a and b). At the latter frequencies, the peaks of the amplitudes are less visible. Thus, a very high level of vibrations is generated by the frequency of the stiffness connection properties and a high level of vibration in the latter frequency covers the amplitudes of vibrations of other frequencies. When
there is a slight increase in vibration amplitudes at resonant frequencies generated by the features of the system's force and energy connection, these are approximately at 22.5 and 18.5Hz (Figure 1a and b). At the latter frequencies, the peaks of the amplitudes are less visible. Thus, a very high level of vibrations is generated by the frequency of the stiffness connection properties and a high level of vibration in the latter frequency covers the amplitudes of vibrations of other frequencies. When 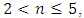 then due to high damping in the system, the vibration level decreases very strongly, as the excitation frequency of the system increases and resonance frequency vibrations are almost invisible (Figure 1a).
then due to high damping in the system, the vibration level decreases very strongly, as the excitation frequency of the system increases and resonance frequency vibrations are almost invisible (Figure 1a).
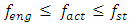 Hz frequency range. From the data in Table 1 and the vibration spectrum in Figure 2, it can be seen that the dynamic system has approximately 27Hz and other resonant frequencies that do not exist in the resonant frequencies of subsystems {31.85, 22.52, 18.34, 12.99}.
Hz frequency range. From the data in Table 1 and the vibration spectrum in Figure 2, it can be seen that the dynamic system has approximately 27Hz and other resonant frequencies that do not exist in the resonant frequencies of subsystems {31.85, 22.52, 18.34, 12.99}.
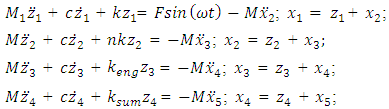
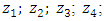
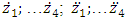 are velocity and acceleration; F is amplitude of excitation force;
are velocity and acceleration; F is amplitude of excitation force; 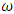 is angular frequency; t is time.After a simple transformation of the system of equations (1) we obtain:
is angular frequency; t is time.After a simple transformation of the system of equations (1) we obtain: 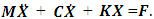
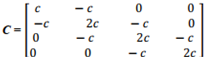
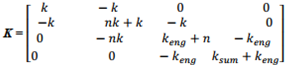
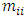 = M when i = 1; 2; ...; 4 In this way, the systems of left equations (2) are clear because the matrices of mass, damping coefficient (3) and stiffness (4) are known. How the matrix F is formed is studied in detail [21]. It is very important to make sure how much the resonant frequencies (eigenvalues) will change when the latter subsystems are combined into a common system. Thus, the system of equations (2) is transformed as follows:
= M when i = 1; 2; ...; 4 In this way, the systems of left equations (2) are clear because the matrices of mass, damping coefficient (3) and stiffness (4) are known. How the matrix F is formed is studied in detail [21]. It is very important to make sure how much the resonant frequencies (eigenvalues) will change when the latter subsystems are combined into a common system. Thus, the system of equations (2) is transformed as follows: 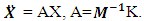
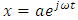 . By inserting
. By inserting 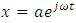 in to the system (5) and denoting
in to the system (5) and denoting 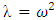 we obtain:
we obtain: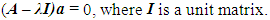
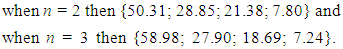
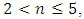 then the frequencies of the latter amplitudes change in the order (see Figure 2e):
then the frequencies of the latter amplitudes change in the order (see Figure 2e):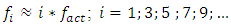
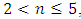 then the frequencies of vibration in a nonlinear dynamic system are identical to the frequencies of parametric vibration. However, at low system vibration frequencies, peaks in the vibration amplitudes may occur at low resonance frequencies or at subharmonic frequencies, but their magnitudes are small. When
then the frequencies of vibration in a nonlinear dynamic system are identical to the frequencies of parametric vibration. However, at low system vibration frequencies, peaks in the vibration amplitudes may occur at low resonance frequencies or at subharmonic frequencies, but their magnitudes are small. When 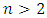 and is an even number, then its parametric vibration frequency amplitudes
and is an even number, then its parametric vibration frequency amplitudes 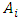 when i = 1, 3, 5, 7,… will be significantly higher than
when i = 1, 3, 5, 7,… will be significantly higher than 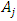 when j = 2,4,6... So, sometimes their vibrations in the spectral density can not always visible. Meanwhile, when
when j = 2,4,6... So, sometimes their vibrations in the spectral density can not always visible. Meanwhile, when 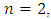 then the dependence of the frequency of the largest vibration amplitudes on the frequency of the system
then the dependence of the frequency of the largest vibration amplitudes on the frequency of the system 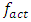 is complex and requires additional and careful research. Therefore, on the basis of the research results, it can be stated that in a vibrating nonlinear dynamic system with a constant value of its parameters, for each value of the excitation force there is a set of potential vibration frequencies (band), which is composed of subsystems and the resonant frequency of the system, their harmonic and subharmonic frequencies. In other words, in a nonlinear dynamic system there is a graded (discretized) space of potential vibration frequencies and a set of parametric forces acting on it, as well as sets of maximum amplitude vibrations and frequencies. The frequency space of potential vibrations, the set of parametric forces acting on it, and the set of system vibrations with the highest amplitude are shown in Figure 2. In Figure 2, resonance frequencies of the subsystem and the whole (general) system when the system is acted at the selected frequency
is complex and requires additional and careful research. Therefore, on the basis of the research results, it can be stated that in a vibrating nonlinear dynamic system with a constant value of its parameters, for each value of the excitation force there is a set of potential vibration frequencies (band), which is composed of subsystems and the resonant frequency of the system, their harmonic and subharmonic frequencies. In other words, in a nonlinear dynamic system there is a graded (discretized) space of potential vibration frequencies and a set of parametric forces acting on it, as well as sets of maximum amplitude vibrations and frequencies. The frequency space of potential vibrations, the set of parametric forces acting on it, and the set of system vibrations with the highest amplitude are shown in Figure 2. In Figure 2, resonance frequencies of the subsystem and the whole (general) system when the system is acted at the selected frequency 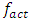 are shown above the line. Subsystem resonant frequencies are marked in bold black color and values of the whole (general) system resonant frequency – in bold green. In order not to darken the image too much, harmonic and subharmonic vibration frequencies are not shown above the line. At the bottom of the dash, there are the values of the excitation parametric forces and the system's largest vibration amplitudes. Parametric exciting forces are marked in red and values with the largest amplitudes in bold blue. From the vibration spectral density in Figure 2d, it can be seen that although the dynamic system is excited at the frequency of
are shown above the line. Subsystem resonant frequencies are marked in bold black color and values of the whole (general) system resonant frequency – in bold green. In order not to darken the image too much, harmonic and subharmonic vibration frequencies are not shown above the line. At the bottom of the dash, there are the values of the excitation parametric forces and the system's largest vibration amplitudes. Parametric exciting forces are marked in red and values with the largest amplitudes in bold blue. From the vibration spectral density in Figure 2d, it can be seen that although the dynamic system is excited at the frequency of 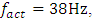 , the maximum vibration amplitude
, the maximum vibration amplitude 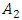 is excited at the frequency of 23.11Hz. Analyzing the set of frequencies (11), we will notice that the frequency of 7.35 Hz, which is the lowest resonant frequency of the whole system, is about 5 times repeated for the excitation frequency of 38 Hz and approximately three times repeated for the frequency of 22.5 Hz generated by the characteristic of the force connection. In this way, the system's acting frequencies do not have to be repeated for low-frequency resonant frequencies and subharmonic frequencies. In the Figure 2d, for clarity, the following frequency zones are shown additionally in the vibrational spectral density: SH - subharmonic; R SH H - resonance, harmonic and subharmonic; R H - resonance and harmonics, and H - harmonic frequencies of the approximate bands. It can also be seen from Figure 1 and Table 1 that when the excitation frequency is higher than the system resonant frequency
is excited at the frequency of 23.11Hz. Analyzing the set of frequencies (11), we will notice that the frequency of 7.35 Hz, which is the lowest resonant frequency of the whole system, is about 5 times repeated for the excitation frequency of 38 Hz and approximately three times repeated for the frequency of 22.5 Hz generated by the characteristic of the force connection. In this way, the system's acting frequencies do not have to be repeated for low-frequency resonant frequencies and subharmonic frequencies. In the Figure 2d, for clarity, the following frequency zones are shown additionally in the vibrational spectral density: SH - subharmonic; R SH H - resonance, harmonic and subharmonic; R H - resonance and harmonics, and H - harmonic frequencies of the approximate bands. It can also be seen from Figure 1 and Table 1 that when the excitation frequency is higher than the system resonant frequency 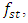 then the vibration amplitudes are small. The results of the research presented above show that by choosing properly the nonlinear dynamic parameters of the system and the excitation force frequency, it is possible to reduce the level of vibrations in the system.
then the vibration amplitudes are small. The results of the research presented above show that by choosing properly the nonlinear dynamic parameters of the system and the excitation force frequency, it is possible to reduce the level of vibrations in the system. 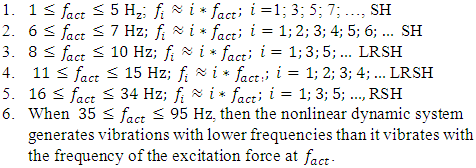
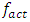 is higher than the frequency
is higher than the frequency 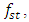 then the vibrations in the spectrum appear at a lower frequency than
then the vibrations in the spectrum appear at a lower frequency than 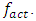 Therefore, when choosing the system excitation force frequency, it is necessary to consider cases of possible resonance in the designed system. Sometimes, when
Therefore, when choosing the system excitation force frequency, it is necessary to consider cases of possible resonance in the designed system. Sometimes, when 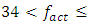
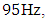 the vibration amplitude
the vibration amplitude 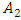 can be higher than
can be higher than 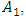 generated by vibrating the system at
generated by vibrating the system at 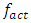 frequency (see Figure 2 and 3). However, when the excitation frequency
frequency (see Figure 2 and 3). However, when the excitation frequency 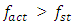 and the magnitude of the excitation force does not change (constant), then the system has a very low vibration level (see Figure 1). While analyzing the results of the study of the influence of the excitation force frequency on the vibration frequencies of the system, it was found that: – when the excitation frequency of the system is higher than the frequency
and the magnitude of the excitation force does not change (constant), then the system has a very low vibration level (see Figure 1). While analyzing the results of the study of the influence of the excitation force frequency on the vibration frequencies of the system, it was found that: – when the excitation frequency of the system is higher than the frequency 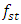 created by the characteristics of the stiffness connection, that is, when
created by the characteristics of the stiffness connection, that is, when 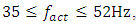 then the dynamic system can vibrate at some subsystem, the whole system and their subharmonics at resonant frequencies (see Fig. 2c), and there may be more than two of them;– when the dynamic system is vibrated with a frequency of
then the dynamic system can vibrate at some subsystem, the whole system and their subharmonics at resonant frequencies (see Fig. 2c), and there may be more than two of them;– when the dynamic system is vibrated with a frequency of 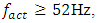 then very low-frequency vibrations occur in it, the frequency of which is the subharmonic frequency
then very low-frequency vibrations occur in it, the frequency of which is the subharmonic frequency 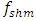 of the lowest resonant frequency of the system. And the dynamic system vibrates with only two frequencies, the excitation frequency and one of the system's low resonant frequencies or some subharmonic frequencies, which repeat the excitation frequency (see Table 1 and Figure 2 and 3). Also, from the result of Table 1 and Figure 3, it can be seen that when the nonlinear dynamic system is excited with the frequency
of the lowest resonant frequency of the system. And the dynamic system vibrates with only two frequencies, the excitation frequency and one of the system's low resonant frequencies or some subharmonic frequencies, which repeat the excitation frequency (see Table 1 and Figure 2 and 3). Also, from the result of Table 1 and Figure 3, it can be seen that when the nonlinear dynamic system is excited with the frequency 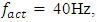 then it generates vibrations with a frequency of approximately 20Hz, with amplitude higher than the excitation frequency of 40 Hz. In this way, it seems that the system is excited at a frequency of 20Hz, because the vibration level is the highest at the latter frequency, and then the vibration frequencies of the system seem to change in this order:
then it generates vibrations with a frequency of approximately 20Hz, with amplitude higher than the excitation frequency of 40 Hz. In this way, it seems that the system is excited at a frequency of 20Hz, because the vibration level is the highest at the latter frequency, and then the vibration frequencies of the system seem to change in this order: 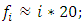 i = 1; 2; 3; 4… (Figure 3a). In this way, the statement in the work [20] is confirmed, that in a nonlinear dynamic system, high-amplitude vibrations generate acting forces. The spectra of the simplified spatial spectral density shown in Figure 2 and 3 have been examined above, in the following material we will call the frequency band of the spectral density, which is generated for the system excitation frequency
i = 1; 2; 3; 4… (Figure 3a). In this way, the statement in the work [20] is confirmed, that in a nonlinear dynamic system, high-amplitude vibrations generate acting forces. The spectra of the simplified spatial spectral density shown in Figure 2 and 3 have been examined above, in the following material we will call the frequency band of the spectral density, which is generated for the system excitation frequency 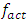 of a certain size.
of a certain size.
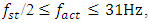 then the maximum vibration frequency of the system varies approximately according to the law:
then the maximum vibration frequency of the system varies approximately according to the law: 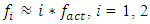 and when
and when 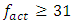 then
then 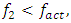 i.e. vibrations are generated at subharmonic frequencies that are multiples of the excitation frequency. In addition, it has been determined that in the considered case the resonance frequencies of the general dynamic system, their subharmonic and harmonic frequencies are more visible in the vibration spectral density, and the maximum vibration size is approximately reached at the frequency of 28 - 29 Hz, i.e. at the third largest resonant frequency of the overall system.– when 0.8 < F/k < 1.77, then the frequencies of the dynamic system vibrations with the largest amplitudes will change approximately according to the specified laws (9);– when F/k >1.77 and
i.e. vibrations are generated at subharmonic frequencies that are multiples of the excitation frequency. In addition, it has been determined that in the considered case the resonance frequencies of the general dynamic system, their subharmonic and harmonic frequencies are more visible in the vibration spectral density, and the maximum vibration size is approximately reached at the frequency of 28 - 29 Hz, i.e. at the third largest resonant frequency of the overall system.– when 0.8 < F/k < 1.77, then the frequencies of the dynamic system vibrations with the largest amplitudes will change approximately according to the specified laws (9);– when F/k >1.77 and 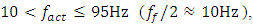 then the dynamic system vibrates at approximately the following frequencies:
then the dynamic system vibrates at approximately the following frequencies: 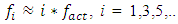 When the system's excitation frequency
When the system's excitation frequency 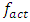 coincides with or has multiple lower resonance frequencies, its subharmonic and harmonic frequencies, the system vibrates at the system's lowest resonant frequency or subharmonic frequency. However, at higher frequencies, when
coincides with or has multiple lower resonance frequencies, its subharmonic and harmonic frequencies, the system vibrates at the system's lowest resonant frequency or subharmonic frequency. However, at higher frequencies, when 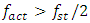 , the amplitudes of the dynamic system's vibrations decrease significantly as the values of i increase, and the vibration amplitudes are significant only when i = 1,3 or even when i = 1.In this way, it is determined that when a low-frequency subharmonic or a lower resonance frequency is a multiple of the excitation frequency
, the amplitudes of the dynamic system's vibrations decrease significantly as the values of i increase, and the vibration amplitudes are significant only when i = 1,3 or even when i = 1.In this way, it is determined that when a low-frequency subharmonic or a lower resonance frequency is a multiple of the excitation frequency  and
and 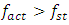 , its vibration level is higher than the size of the vibration generated by the
, its vibration level is higher than the size of the vibration generated by the 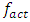 frequency (see Figure 3a and 3c). It was also found that the response of the nonlinear dynamic system to the magnitude of the excitation force is twofold: when F/k > 0.8, then the main resonance in the system corresponds to the frequency generated by the characteristics of the stiffness connection (see Fig. 1a) and when F/k < 0.8, then it corresponds to the third resonant frequency of the whole system in terms of magnitude, which is in the range of 28 - 29Hz. In this way, according to recent research results, when the frequency of excitation is in the interval
frequency (see Figure 3a and 3c). It was also found that the response of the nonlinear dynamic system to the magnitude of the excitation force is twofold: when F/k > 0.8, then the main resonance in the system corresponds to the frequency generated by the characteristics of the stiffness connection (see Fig. 1a) and when F/k < 0.8, then it corresponds to the third resonant frequency of the whole system in terms of magnitude, which is in the range of 28 - 29Hz. In this way, according to recent research results, when the frequency of excitation is in the interval 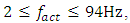 it is determined:– resonant, harmonic and subharmonic frequencies of constant size space, and two-dimensional arrays of dynamic systems with the largest vibration amplitudes and frequencies in each section of the plane B0f (see Figure 2 and 3); – three-dimensional spatial array of vibrational spectral density SD, in which the values of the vibration amplitude, their frequency and the system's excitation frequency will vary. It means that the vibration spectral density space SD can be defined (described) by a three-dimensional matrix (array), which is specified using three indices: block size
it is determined:– resonant, harmonic and subharmonic frequencies of constant size space, and two-dimensional arrays of dynamic systems with the largest vibration amplitudes and frequencies in each section of the plane B0f (see Figure 2 and 3); – three-dimensional spatial array of vibrational spectral density SD, in which the values of the vibration amplitude, their frequency and the system's excitation frequency will vary. It means that the vibration spectral density space SD can be defined (described) by a three-dimensional matrix (array), which is specified using three indices: block size 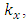 row size
row size 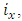 and column size
and column size 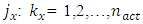 – the number of excitation force frequencies
– the number of excitation force frequencies 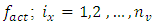 – the number of vibration frequencies of a nonlinear dynamic system
– the number of vibration frequencies of a nonlinear dynamic system 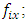
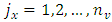 – the number of vibration amplitudes of a nonlinear dynamic system. In this way, it is shown that for all values of the excitation frequency
– the number of vibration amplitudes of a nonlinear dynamic system. In this way, it is shown that for all values of the excitation frequency 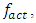 the upper part of the graph in Figures 2 and 3 is an invariant (constant) part and includes the resonant frequencies of the system subsystems and the whole system, their subharmonic and harmonic frequencies. The changing part of the spectral density space will be only a part (a set) of the frequencies generated by the system and a set of the maximum amplitudes of the system's vibrations. In this way, the spectral density of the nonlinear dynamic system in the potential frequency space is determined according to the mathematical apparatus presented in previous works [20,21] and their magnitudes are described by the following sets:
the upper part of the graph in Figures 2 and 3 is an invariant (constant) part and includes the resonant frequencies of the system subsystems and the whole system, their subharmonic and harmonic frequencies. The changing part of the spectral density space will be only a part (a set) of the frequencies generated by the system and a set of the maximum amplitudes of the system's vibrations. In this way, the spectral density of the nonlinear dynamic system in the potential frequency space is determined according to the mathematical apparatus presented in previous works [20,21] and their magnitudes are described by the following sets: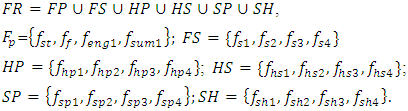
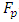 – set of resonant frequencies of subsets system; FS – subset of resonant frequencies of system; HP – subset of resonant frequency harmonics of subsystem; HS – subset of resonant frequency harmonics of system; SP – subset of resonant frequency subharmonics of subsystem; SH – subset of resonant frequency harmonics of system. For example, in the considered case where n = 2, the set of FR will have approximately the following frequency values:
– set of resonant frequencies of subsets system; FS – subset of resonant frequencies of system; HP – subset of resonant frequency harmonics of subsystem; HS – subset of resonant frequency harmonics of system; SP – subset of resonant frequency subharmonics of subsystem; SH – subset of resonant frequency harmonics of system. For example, in the considered case where n = 2, the set of FR will have approximately the following frequency values: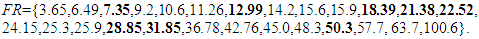
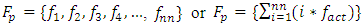
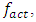 the set of parametric excitation force sizes
the set of parametric excitation force sizes 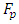 will be different. In this way, the parametric forces of the set
will be different. In this way, the parametric forces of the set 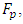 in interaction with the dynamic properties of the system and the frequency set FR of the spectral density space, for each excitation force
in interaction with the dynamic properties of the system and the frequency set FR of the spectral density space, for each excitation force 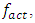 will generate the vibrational spectral density of the latter space in the plane B0f (see Figure 2 and 3). In fact, for each excitation force, the vibrations of the system will be described by a two-dimensional array, one row of which will contain the maximum vibration amplitudes, and the second row will contain the vibration frequencies of the system, corresponding to the order of presentation of the vibration amplitudes:
will generate the vibrational spectral density of the latter space in the plane B0f (see Figure 2 and 3). In fact, for each excitation force, the vibrations of the system will be described by a two-dimensional array, one row of which will contain the maximum vibration amplitudes, and the second row will contain the vibration frequencies of the system, corresponding to the order of presentation of the vibration amplitudes: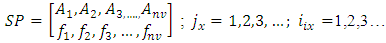
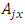 – amplitudes of nonlinear dynamic system vibrations;
– amplitudes of nonlinear dynamic system vibrations; 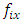 – vibration frequencies of a nonlinear dynamic system.To determine the vibration frequencies of nonlinear dynamic systems, it is convenient to use the methodology set out above (see Figure 2 and 3), which allows creating a potential spectral density frequency band for each excitation force and using the determined system characteristics (features) (8); (9); (10); (13) to create an approximate one-dimensional array of vibration frequencies
– vibration frequencies of a nonlinear dynamic system.To determine the vibration frequencies of nonlinear dynamic systems, it is convenient to use the methodology set out above (see Figure 2 and 3), which allows creating a potential spectral density frequency band for each excitation force and using the determined system characteristics (features) (8); (9); (10); (13) to create an approximate one-dimensional array of vibration frequencies 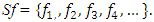 When the vibration frequencies of nonlinear dynamical systems are determined, then the number of unknowns is reduced by two times and the number of unknowns in differential equations will be equal to the number of equations. In order to clarify the physics of nonlinear dynamic system vibrations and to show the suitability of the considered method for vibration analysis and the possibility of reducing vibrations in a nonlinear dynamic system, the acting frequency of 40Hz was chosen not by chance. The latter frequency 40Hz is a harmonic of the frequency
When the vibration frequencies of nonlinear dynamical systems are determined, then the number of unknowns is reduced by two times and the number of unknowns in differential equations will be equal to the number of equations. In order to clarify the physics of nonlinear dynamic system vibrations and to show the suitability of the considered method for vibration analysis and the possibility of reducing vibrations in a nonlinear dynamic system, the acting frequency of 40Hz was chosen not by chance. The latter frequency 40Hz is a harmonic of the frequency 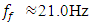 generated by the peculiarities of the system's force connections. However, let's examine the vibrations of the dynamic system of the latter case and the stability of its operation. We will perform the study of nonlinear dynamic system vibration magnitude dependences on the excitation frequency and force size with the help of MATLAB. For example, when the magnitude of the excitation force is F=100000N and the system vibrates at 40Hz. it is
generated by the peculiarities of the system's force connections. However, let's examine the vibrations of the dynamic system of the latter case and the stability of its operation. We will perform the study of nonlinear dynamic system vibration magnitude dependences on the excitation frequency and force size with the help of MATLAB. For example, when the magnitude of the excitation force is F=100000N and the system vibrates at 40Hz. it is 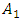 = -14.304(40Hz));
= -14.304(40Hz)); 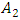 = -9.749(20.09Hz) and
= -9.749(20.09Hz) and 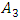 = -48.872 (80.0Hz), and when the system is vibrated with F=200000N force, then at the same frequency
= -48.872 (80.0Hz), and when the system is vibrated with F=200000N force, then at the same frequency 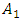 = 4.514(40Hz);
= 4.514(40Hz); 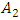 = -27.552(120Hz). It can be seen from the latest data that when the force is doubled, the amplitude of the largest vibrations has increased
= -27.552(120Hz). It can be seen from the latest data that when the force is doubled, the amplitude of the largest vibrations has increased 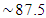 times:
times: 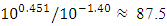 . When the acting frequency is not 40Hz, but
. When the acting frequency is not 40Hz, but 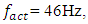 and F= 200000N then the vibration amplitudes of the latter system are greatly reduced, compared to the frequency when the system vibrates
and F= 200000N then the vibration amplitudes of the latter system are greatly reduced, compared to the frequency when the system vibrates 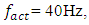 at F=200000N:
at F=200000N: 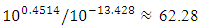 times and will be of small magnitude. The latter frequency was chosen because it is between 40Hz - the harmonic frequency and 50.31Hz - the resonant frequency of the system. The vibrations at the resonant frequency of 18.59Hz (see Figure 3d), is very small. In this way, when
times and will be of small magnitude. The latter frequency was chosen because it is between 40Hz - the harmonic frequency and 50.31Hz - the resonant frequency of the system. The vibrations at the resonant frequency of 18.59Hz (see Figure 3d), is very small. In this way, when 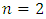 the results of the last calculation show that when the excitation frequency is higher than the resonance frequency of the subsystem, generated by the features of the stiffness connection and F/k > 0.8, the level of nonlinear dynamic vibrations of the system will be minimal and the system will work stably only when the constancy of the excitation frequency and its force magnitude is guaranteed. Even variable nonlinear dynamic load of the system (variable internal friction size of the system and disturbances of other stimuli) can cause changes in the magnitude of force F and, as a result, non-stable working conditions can be created for the system. If the latter requirements are not ensured, the dynamic vibration level of the system may change periodically even several tens of times, in addition, a jumpy (pulsating) working mode will be felt and the system will work unstable. The significance of the spatial frequency band of vibration spectral density in the study and design of new systems is shown. When the degree of nonlinearity of the dynamic system is within the limits of
the results of the last calculation show that when the excitation frequency is higher than the resonance frequency of the subsystem, generated by the features of the stiffness connection and F/k > 0.8, the level of nonlinear dynamic vibrations of the system will be minimal and the system will work stably only when the constancy of the excitation frequency and its force magnitude is guaranteed. Even variable nonlinear dynamic load of the system (variable internal friction size of the system and disturbances of other stimuli) can cause changes in the magnitude of force F and, as a result, non-stable working conditions can be created for the system. If the latter requirements are not ensured, the dynamic vibration level of the system may change periodically even several tens of times, in addition, a jumpy (pulsating) working mode will be felt and the system will work unstable. The significance of the spatial frequency band of vibration spectral density in the study and design of new systems is shown. When the degree of nonlinearity of the dynamic system is within the limits of 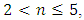 then when the magnitude of the excitation force changes in the interval
then when the magnitude of the excitation force changes in the interval 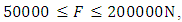 only the magnitude of the vibrations changes, but the frequency spectrum is constant. So, when n = 2, the possibilities to significantly reduce the level of vibration in the system are explained and demonstrated, the processes taking place in it are clarified. In this way, the research results show that when
only the magnitude of the vibrations changes, but the frequency spectrum is constant. So, when n = 2, the possibilities to significantly reduce the level of vibration in the system are explained and demonstrated, the processes taking place in it are clarified. In this way, the research results show that when 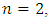 then if the system does not have any restrictions on working modes, then the lower vibration level in the nonlinear dynamic system will take place if the excitation frequency satisfies the condition:
then if the system does not have any restrictions on working modes, then the lower vibration level in the nonlinear dynamic system will take place if the excitation frequency satisfies the condition: 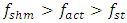 , and when
, and when 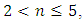 then it should be:
then it should be: 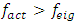 . In both of the latter cases, the excitation frequency must not coincide with or be close to, or a multiple of, the resonant frequencies of the nonlinear dynamic system, its harmonic and subharmonic frequencies. In this way, the research results show that there are three kinds (types) of vibrations in the nonlinear dynamic system: system resonance, parametric and systems. Therefore, knowing the latter types of frequencies of the nonlinear dynamic system and using the spectral density frequency band method discussed above, it is possible to choose the appropriate excitation frequency of the system and significantly reduce its vibration level. And if it is not possible to change the excitation frequency of the system, then it is possible to change the main parameters of the system and in this way create conditions so that excitation frequency does not coincide with its resonant frequencies.
. In both of the latter cases, the excitation frequency must not coincide with or be close to, or a multiple of, the resonant frequencies of the nonlinear dynamic system, its harmonic and subharmonic frequencies. In this way, the research results show that there are three kinds (types) of vibrations in the nonlinear dynamic system: system resonance, parametric and systems. Therefore, knowing the latter types of frequencies of the nonlinear dynamic system and using the spectral density frequency band method discussed above, it is possible to choose the appropriate excitation frequency of the system and significantly reduce its vibration level. And if it is not possible to change the excitation frequency of the system, then it is possible to change the main parameters of the system and in this way create conditions so that excitation frequency does not coincide with its resonant frequencies.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML