M. V. Crankson, H. Otoo, P. K. Nyarko, H. Cobbina
Department of Mathematical Sciences, University of Mines and Technology, Tarkwa, Ghana
Correspondence to: M. V. Crankson, Department of Mathematical Sciences, University of Mines and Technology, Tarkwa, Ghana.
| Email: |  |
Copyright © 2023 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Businesses are constantly looking for more effective methods to increase revenue and decrease costs in order to maximize profit. Transportation has been the major expenditure affecting the profit of companies. The cost of transportation whenever it increases causes profit to decrease. This paper focuses on solving the transportation problem of a mining company in Tarkwa. The Modified Vogel’s Approximation Method is employed to find an initial basic feasible solution to the transportation problem such that the total cost is minimized since it is well known for obtaining good primal solution of a wide range of transportation problems. It is established that the mine will save an amount of of GH¢ 996,315 within an eight months period if they employ this method in their allocation.
Keywords:
Transportation problem, Modified Vogel’s Approximation Method, Objective Function, Constraints, Optimal Solution
Cite this paper: M. V. Crankson, H. Otoo, P. K. Nyarko, H. Cobbina, Modified Vogel’s Approximation Method for Finding Optimal Solution of Transportation Problem: A Case Study at a Mining Company, American Journal of Computational and Applied Mathematics , Vol. 13 No. 1, 2023, pp. 15-20. doi: 10.5923/j.ajcam.20231301.03.
1. Introduction
Linear Programming Problems are the most often utilized mathematical applications in business, government, and industry. The goal of linear programming is to minimize (or maximize) a linear objective function in n real variables subject to a (finite) set of linear constraints, which can be either equations or inequalities [3].The Transportation Problem (TP) is a special form of Linear Programming Problem (LPP), which seeks to identify the distribution strategy that will allow for the most economical movement of goods from many sources (such as factories) to various destinations (such as warehouses), while still meeting demand and supply constraints [10]. It aids in knowing how much demand there will be for a commodity at each of the many different destinations, and also how much it will cost to transport one unit of the commodity between each pair of source and destination [1]. However, the cost per unit of transportation does not change throughout the course of time. In Ghana, there is still a substantial reliance on manual labour for the movement of products. This can be solved by creating a transportation system that is both strong and efficient. The industries could be impacted by an effective transportation system since it could lower manufacturing costs and retail prices of everyday essentials. In general, the transportation model can be used to situations other than the direct conveyance of a commodity, such as inventory management, scheduling employee hours, and staff placement [5]. Gold production companies in Ghana contribute greater to the Gross Domestic Product (GDP) of the country’s economy in terms of social responsibilities, employment, and sometimes sponsorship for students within their catchment areas. Transportation has been one of the major takes that reduces the profit of mining companies in Ghana since the company transports its workers to and from work on a daily basis. It is therefore essential for transportation models to be developed to help reduce their total cost while satisfying their employees.The Modified Vogel’s Approximation Method (MVAM) is considered to be the best method in computing the initial basic feasible solution to a transportation problem, as it provides better results when compared to other methods. It involves calculating the penalty (difference between the lowest cost and the second-lowest cost) for each row and column of the cost-matrix, and then assigning the maximum number of units possible to the least-cost cell in the row or column with the largest penalty.A modified Vogel Approximation Method was proposed by [2] in solving balanced transportation problems in linear programming. The method was shown to be better in comparison with other existing methods (excluding Vogel Approximation Method) since it minimizes overall cost (relatively) as well as unit cost in its solution algorithm, just like the Vogel Approximation Method.[8] found initial basic feasible solutions to transportation problems using the Modified Vogel’s Approximation Method. The solutions were compared with that of three other methods; North West Corner Method, Least Cost Method and Vogel’s Approximation Method. It was discovered that the Modified Vogel's Approximation Method offered the minimum transportation cost and optimal solution. Moreover, the result of the Modified Vogel’s Approximation Method was the same as the Vogel’s Approximation Method in some cases, and in all better than the other two methods.The Vogel’s Approximation Method was also modified by [7] to address the optimality of a transportation problem by statistical techniques. Compared to the existing methods such as North West Corner Method (NWCM), Least Cost Method (LCM) and Vogel’s Approximation Method (VAM), the modified method offered a better feasible solution. The validation of their method was done using examples from literature to examine the authenticity and optimality of the solution.Another effective heuristic method was modified over the Vogel's Approximation Method to solve transportation problems. In comparison to the solutions produced by the North-West Corner Method, Minimum Cost Method, and Vogel's Approximation Method, this algorithm provided a better initial basic feasible solution to the transportation problem. Additionally, it was equal to the optimal solution in some circumstances, and the technique is thought to be efficient for both big and small sizes of data [4]. In order to address the fuzzy transportation problem which is a well-known optimization problem in the area of fuzzy set and system, [6] made yet another modification to the conventional Vogel Approximation Method algorithm. Their algorithm was created to resolve a fuzzy transportation problem with interval type 2 fuzzy values for supply, demand, and expense of transportation. To establish the effectiveness of the algorithm, two numerical examples were taken into consideration.This paper seeks to use the Modified Vogel Approximation Method, which is well known for its effectiveness, to model the transportation system at a mining company as a linear programming problem and to find the optimal cost of transportation.
2. Materials and Methods
2.1. Network Representation of Transportation Problem
The transportation problem is focused on determining the optimal distribution plan for a specific commodity. An item is regarded as having a known quantity that is distributed among several sources and a known demand at each of the numerous destinations. Between each source and destination pair, is also a known transportation cost. The unit transportation cost is constant in the simplest scenario. The challenge is to identify the best distribution strategy for moving the goods from their sources to their final destinations while reducing the overall cost of transportation. This is demonstrated in Figure 1.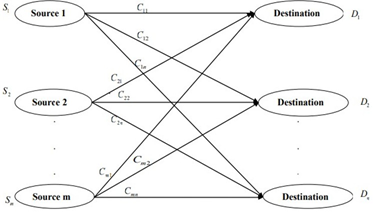 | Figure 1. Network Representation of Transportation Problem |
2.2. Data Acquisition
Data from a mine database, including the pick-up points and destinations used in this research, was gathered between the months of January and August of 2022. The company employs a transport servicing company in transporting its employees.All things being equal, the buses that transport the employees follow a consistent routine, so all the data entries for the months of January to August, 2022 remain the same. In light of this, the transport servicing company modifies them consistently throughout the month depending on the days in the month.The transport service provider considers the to and fro of the employees in their charges per each pickup point to the company. With regard to our evaluation, there has been a monetary conversion of the daily rate from $ to GH¢, since the total charges are in Ghana cedis, as such, the company also pays in Ghana cedis.
2.3. Model Formulation
Assuming a company has m warehouses and n retails or distribution locations. A unit product is to be transported from the warehouses to the retailer or distributor. Each distributor or retailer has a specific level of demand, and each warehouse has a specific level of availability. Every pair of warehouses and distributors has a documented transportation cost. It is assumed that these costs are linear. The following conditions are considered in the formulation:1. the total source of the workers denoted by 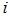 where
where 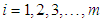 . 2. the total destination of the buses denoted by
. 2. the total destination of the buses denoted by  where
where 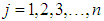 .3. the cost of conveying workers of the company from source
.3. the cost of conveying workers of the company from source 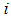 to destination
to destination 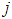 is equal to
is equal to 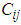 , where
, where 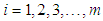 and
and 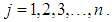 According to the data, the primary pick up points were considered to be seven (7), thus
According to the data, the primary pick up points were considered to be seven (7), thus 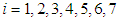 . Given that the daily charges cover both the to and fro directions, the destinations were considered to be
. Given that the daily charges cover both the to and fro directions, the destinations were considered to be 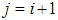 with the view that some employees alight at locations which are not pick up spots. Table 1 shows the summary of the monthly charges from seven (7) different sources to eight (8) different destinations.
with the view that some employees alight at locations which are not pick up spots. Table 1 shows the summary of the monthly charges from seven (7) different sources to eight (8) different destinations. Table 1. Summary of Allocations with Monthly Charges
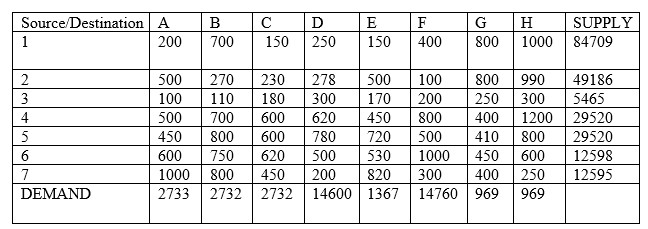 |
| |
|
2.3.1. Formulation of the Objective Function
The linear programming optimization problem is frequently represented and solved using the Objective function where the goal is to optimize profit, reduce cost, or use resources as little as possible. To find the best optimal solution, the objective function is maximized or minimized. Let 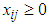 be the number of employees transported from the source
be the number of employees transported from the source 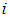 to the destination
to the destination 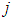 . The mathematical formulation of the objective function is
. The mathematical formulation of the objective function is 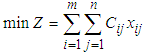 where
where 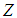 is the total transportation cost to be minimized. From our data set, the objective function
is the total transportation cost to be minimized. From our data set, the objective function 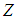 is formulated as Equation (1).
is formulated as Equation (1).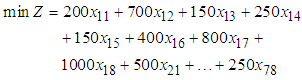 | (1) |
2.3.2. Formulation of the Constraints
Constraints are limitations or restrictions on the overall quantity of a specific resource needed to complete the tasks that determine the degree of success in the decision variables. All constraints are in the form of equations in the standard form of a linear programming problem.Since the decision variables are positive regardless of whether the objective function is being maximized or minimized, the constraints are said to be nonnegative, thus 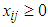 . The mathematical formulation of the constraints are
. The mathematical formulation of the constraints are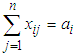 (Supply from sources)
(Supply from sources) 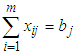 (Demand from destinationswhere
(Demand from destinationswhere 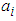 is the level of supply at each source
is the level of supply at each source 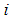 and
and 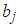 is the level of demand at each destination
is the level of demand at each destination 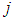 .The following assumptions were considered for the constraints;i. The total amount allocated for source one (1) should not exceed 84709ii. The amount allocated for source two (2) should not exceed 49186iii. A least amount of 5465 is allocated for source three (3)iv. The total amount allocated for source four (4) should not exceed 29520v. The total amount allocated for source five (5) should be at least 29520vi. The total amount allocated for source six (6) should be at least 12598vii. The total amount allocated for source seven (7) should be at least 12595Thus, the seven (7) constraints governing the objective function are formulated as Equations (2) to (8).
.The following assumptions were considered for the constraints;i. The total amount allocated for source one (1) should not exceed 84709ii. The amount allocated for source two (2) should not exceed 49186iii. A least amount of 5465 is allocated for source three (3)iv. The total amount allocated for source four (4) should not exceed 29520v. The total amount allocated for source five (5) should be at least 29520vi. The total amount allocated for source six (6) should be at least 12598vii. The total amount allocated for source seven (7) should be at least 12595Thus, the seven (7) constraints governing the objective function are formulated as Equations (2) to (8).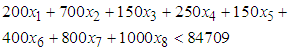 | (2) |
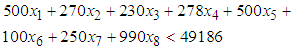 | (3) |
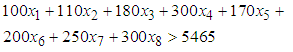 | (4) |
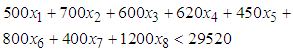 | (5) |
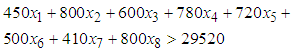 | (6) |
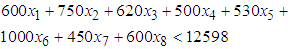 | (7) |
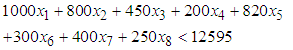 | (8) |
2.4. Modified Vogel’s Approximation Method
Vogel's Approximation Method, which employs a modified form of the simplex method, is the most utilized technique for identifying efficient initial solutions for solving transportation problems. According to this technique, the cost-matrix's penalty, that is, the difference between the lowest cost and the next-lowest cost is calculated for each row and column, and the least cost cell in the row or column with the greatest number of units is assigned the largest penalty. There has been modifications to the Vogel's Approximation Method. Research has shown that in addition to using the Modified Vogel’s Approximation Method to find the initial basic feasible solution, the Modified Vogel’s Approximation Method also provides the minimum transportation cost and, in some instances, the optimal solution. The Modified Vogel’s Approximation Method proposed by [9] is adopted in this study.
2.4.1. Algorithm of the Modified Vogel’s Approximation Method
Step 1. Subtract the largest entry from each of the elements of every row of the transportation table and place them on the left-top of corresponding element.Step 2. Subtract the largest transportation cost from each of the entries of every column of the transportation table and write them on the left-bottom of the corresponding element.Step 3. Form a reduced matrix whose elements are the summation of the left-top and left-bottom elements of Steps 1 and 2.Step 4. Calculate the distribution indicators by subtracting the largest and next-to-largest element of each row and each column of the reduced matrix and write them just after and below of the supply and demand amount respectively.Step 5. Identify the highest distribution indicator, if there are two or more highest indicators, choose the highest indicator along which the least element is present. If there are two or more least elements present, choose any one of them arbitrarily.Step 6. Eliminate the entire Row or Column when Demand or Supply is exhausted.Step 7. Repeat Step 5 and Step 6 till all allocation are done, if done well the figure for the demand and supply will be the same for the last allocation. Step 8. Pull the allocations of the positive allocated cells of the reduced matrix to the original transportation table and calculate the TTC, 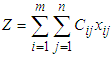 where
where 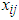 is the total allocation of the
is the total allocation of the 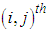 cell and
cell and 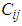 is the corresponding unit transportation cost.
is the corresponding unit transportation cost.
3. Results and Discussions
Applying the Algorithm to the summary in Table 1 yields the results for January to August, 2022 as shown in Tables 2 to 9.Table 2. Result for January, 2022
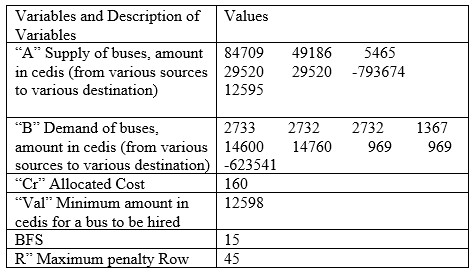 |
| |
|
Table 3. Result for February, 2022
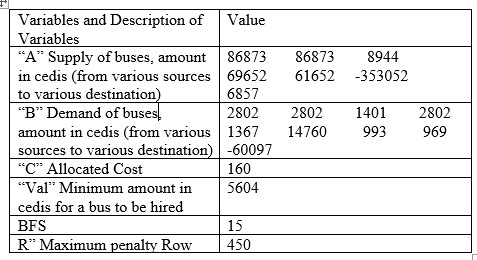 |
| |
|
Table 4. Result for March, 2022
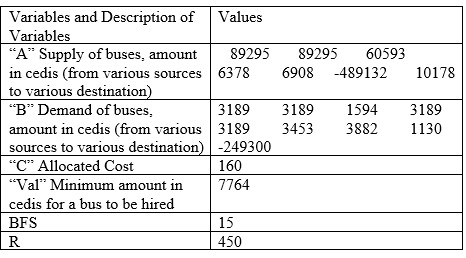 |
| |
|
Table 5. Result for April, 2022
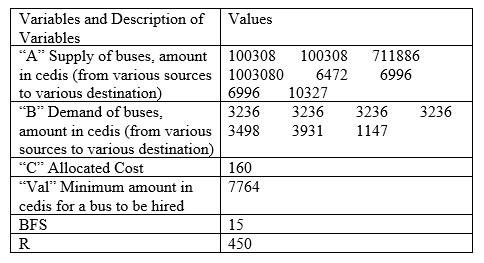 |
| |
|
Table 6. Result for May, 2022
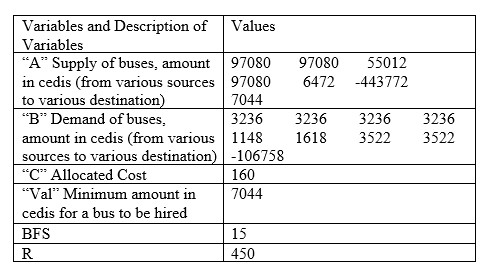 |
| |
|
Table 7. Result for June, 2022
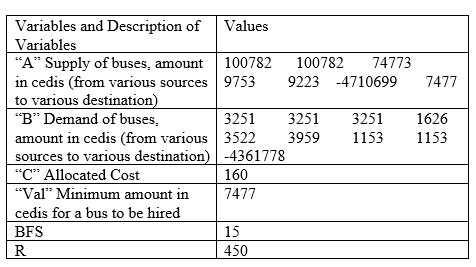 |
| |
|
Table 8. Result for July, 2022
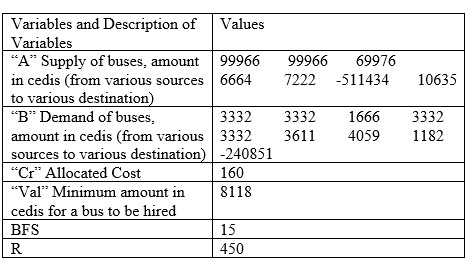 |
| |
|
Table 9. Result for August, 2022
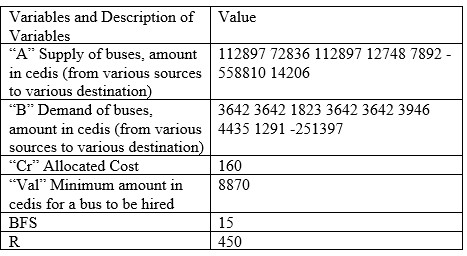 |
| |
|
The monthly charges differ with respect to the number of days in the month. Thus, the ‘val’ is multiplied by the number of days in the respective month to achieve the total cost of transportation. The total cost of transportation for each month is tabulated in Table 10.Table 10. Total Cost of Transportation
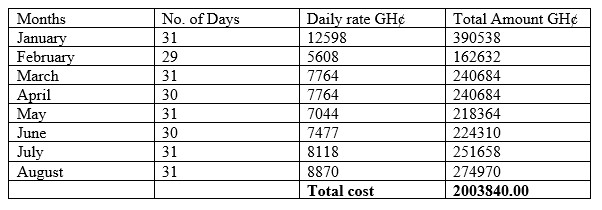 |
| |
|
4. Limitations
The limitations to this work are:i. Each bus has a limited number of passengers it can take.ii. Unit transportation costs are independent of the number of employees on board.iii. Employees’ availability at each pick up points.iv. Supply and demand are known and independent on price charged per an employee.
5. Conclusions
The Modified Vogel’s Approximation Method has been used to obtain a basic feasible solution for the transportation problem at a mining company in Tarkwa. The minimum or least cost of transporting the workers from the various sources to the destination and vice versa is GH¢ 2,003,840. This saves the company an amount of GH¢ 996,315 from the GH¢ 3,000,156 recorded at the end of August, 2022. Mining companies are therefore encouraged to employ the MVAM in their daily schedule to minimize their total transportation cost since most of these companies transports its employees to and from the workplace.
References
| [1] | Adlakha, V. and Kowalski, K., 2009, “Alternate Solutions Analysis for Transportation Problems”, Journal of Business and Economics Research (JBER), 7(11). |
| [2] | Akpan, S., Usen, J. and Ajah, O., 2015, “A Modified Vogel Approximation Method for Solving Balanced Transportation Problems”, American Scientific Research Journal for Engineering, Technology, and Sciences (ASRJETS), 14(3), pp. 289-302. |
| [3] | Edokpia, R. and Amiolemhen, P., 2016, “Transportation Cost Minimization of a Manufacturing Firm using Genetic Algorithm Approach”, Nigerian Journal of Technology, 35(4), pp. 866–873. |
| [4] | Hussein, H. A. and Shiker, M. A. K., 2020, “A Modification to Vogel’s Approximation Method to Solve Transportation Problems”, Journal of Physics: Conference Series, vol. 1591, no. 1, p. 012029, IOP Publishing. |
| [5] | Pandian, P. and Natarajan, G., 2011, “A New Method for Solving Bottleneck-Cost Transportation Problems”, International Mathematical Forum, vol. 6, pp. 451–460. |
| [6] | Pratihar, J., Kumar, R., Edalatpanah, S. A. and Dey, A., 2021, “Modified Vogel’s Approximation Method for Transportation Problem under Uncertain Environment”, Complex and Intelligent Systems, 7(1), pp. 29-40. |
| [7] | Sahito, S., Shaikh, W. A., Shaikh, A. G., Shaikh, A. A. and Shah, S. F., 2021, “Modification of Vogel's Approximation Method for Optimality of Transportation Problem by Statistical Technique”, Quaid-E-Awam University Research Journal of Engineering, Science & Technology, Nawabshah, 19(2), pp. 42-48. |
| [8] | Soomro, A. S., Junaid, M. and Tularam, G. A., 2015, “Modified Vogel’s Approximation Method for Solving Transportation Problems”, Mathematical Theory and Modeling, 5(4), pp. 32-42. |
| [9] | Ullah, M. W., Uddin, M. A. and Kawser, R., 2016, “A Modified Vogel’s Approximation Method for Obtaining a Good Primal Solution of Transportation Problems”, Annals of Pure and Applied Mathematics, 11(1), pp. 63–71. |
| [10] | Varma, N. and Kumar, G., 2015, “Solving Age-Old Transportation Problems by Nonlinear Programming Methods”, IOSR Journal of Mathematics, 11(1), pp.16–18. |




 where
where 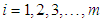 . 2. the total destination of the buses denoted by
. 2. the total destination of the buses denoted by 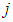 where
where 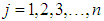 .3. the cost of conveying workers of the company from source
.3. the cost of conveying workers of the company from source 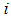 to destination
to destination 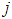 is equal to
is equal to 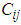 , where
, where 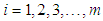 and
and 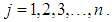 According to the data, the primary pick up points were considered to be seven (7), thus
According to the data, the primary pick up points were considered to be seven (7), thus 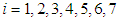 . Given that the daily charges cover both the to and fro directions, the destinations were considered to be
. Given that the daily charges cover both the to and fro directions, the destinations were considered to be 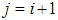 with the view that some employees alight at locations which are not pick up spots. Table 1 shows the summary of the monthly charges from seven (7) different sources to eight (8) different destinations.
with the view that some employees alight at locations which are not pick up spots. Table 1 shows the summary of the monthly charges from seven (7) different sources to eight (8) different destinations. 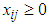 be the number of employees transported from the source
be the number of employees transported from the source 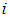 to the destination
to the destination 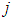 . The mathematical formulation of the objective function is
. The mathematical formulation of the objective function is 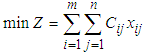 where
where 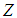 is the total transportation cost to be minimized. From our data set, the objective function
is the total transportation cost to be minimized. From our data set, the objective function 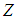 is formulated as Equation (1).
is formulated as Equation (1).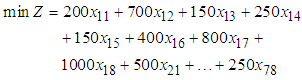
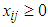 . The mathematical formulation of the constraints are
. The mathematical formulation of the constraints are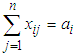 (Supply from sources)
(Supply from sources) 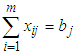 (Demand from destinationswhere
(Demand from destinationswhere 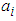 is the level of supply at each source
is the level of supply at each source 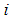 and
and 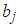 is the level of demand at each destination
is the level of demand at each destination 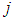 .The following assumptions were considered for the constraints;i. The total amount allocated for source one (1) should not exceed 84709ii. The amount allocated for source two (2) should not exceed 49186iii. A least amount of 5465 is allocated for source three (3)iv. The total amount allocated for source four (4) should not exceed 29520v. The total amount allocated for source five (5) should be at least 29520vi. The total amount allocated for source six (6) should be at least 12598vii. The total amount allocated for source seven (7) should be at least 12595Thus, the seven (7) constraints governing the objective function are formulated as Equations (2) to (8).
.The following assumptions were considered for the constraints;i. The total amount allocated for source one (1) should not exceed 84709ii. The amount allocated for source two (2) should not exceed 49186iii. A least amount of 5465 is allocated for source three (3)iv. The total amount allocated for source four (4) should not exceed 29520v. The total amount allocated for source five (5) should be at least 29520vi. The total amount allocated for source six (6) should be at least 12598vii. The total amount allocated for source seven (7) should be at least 12595Thus, the seven (7) constraints governing the objective function are formulated as Equations (2) to (8).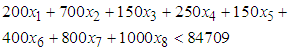
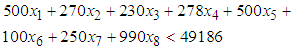
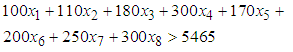
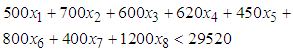
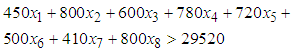
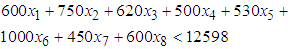
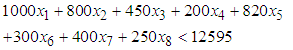
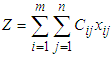 where
where 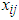 is the total allocation of the
is the total allocation of the 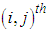 cell and
cell and 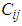 is the corresponding unit transportation cost.
is the corresponding unit transportation cost. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML








