-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2023; 13(1): 1-5
doi:10.5923/j.ajcam.20231301.01
Received: Jun. 1, 2023; Accepted: Jun. 10, 2023; Published: Jun. 12, 2023

Investigating the Link between Energy, Matter, and Information: The E=mc² and Landauer Principle
Boris Menin
Department Mechanical & Refrigeration Expert, Beer-Sheva, Israel
Correspondence to: Boris Menin , Department Mechanical & Refrigeration Expert, Beer-Sheva, Israel.
| Email: |  |
Copyright © 2023 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Albert Einstein's famous equation E=mc², which explains the source of stellar energy and the development of nuclear weapons, is not only practically significant but also fundamental to our understanding of the universe. Recent research shows that information, which is considered a new form of physical matter, is closely linked to this equation, making it an essential part of the physical world. This article discusses the relationship between E=mc² and Landauer's principle, which states that erasing information requires a minimum amount of energy, emphasizing the role of information in the physical universe. By exploring the connection between these equations, the article presents two methods for integration, highlighting their potential for new discoveries in physics.
Keywords: Earth's volume, Einstein, Energy-Mass Equivalence, Information Theory, Information-Energy Equivalence, Landauer, Storage Density
Cite this paper: Boris Menin , Investigating the Link between Energy, Matter, and Information: The E=mc² and Landauer Principle, American Journal of Computational and Applied Mathematics , Vol. 13 No. 1, 2023, pp. 1-5. doi: 10.5923/j.ajcam.20231301.01.
Article Outline
1. Introduction
- The formula E=m·c2 is one of the most famous equations in the history of physics, and it has played a pivotal role in shaping our understanding of nature. The equation was first proposed by Albert Einstein in 1905 as part of his special theory of relativity [1]. In recent years, scientists have explored the idea that information itself can be considered a new form of physical matter, and the E=m·c2 equation has played a crucial role in this development.This concept of information as a physical entity is since information has a physical manifestation in the universe and requires energy to process, store, and transmit. The connection between energy and information is not new, as the concept of information entropy, first introduced by Claude Shannon in 1948 [2], provides a framework for understanding the physical properties of information.It has been shown that the amount of information that can be stored in a physical system is limited by a fundamental bound called the Bekenstein limit [3]. This limitation sets an upper limit on the amount of information that can be contained within a given region of space, based on the mass and energy of that region. The Landauer principle [4], which states that erasing a bit of information requires a minimum amount of energy, is also related to this concept.The relationship between these ideas suggests that information is a fundamental part of the physical universe, and that understanding the physical properties of information is crucial for a complete understanding of the nature of the universe. However, it is important to note that the Landauer principle has been heavily criticized by J.D. Norton [5]. Nonetheless, the Landauer principle has been defended in [6], and the discussion is far from over.While some may criticize the approach that links Einstein's formula to information without a deeper explanation, it is important to note that the significance of information in storage, transmission, and processing was not widely recognized until relatively recently. In the last decade, numerous studies investigating the relationship between E=m·c² and information have been published [7-16], each contributing significantly to our understanding of the nature of information and its role in physics. However, it is important to note that some of the articles have certain limitations that should be considered. For example, Verlinde's review on holography and emergent gravity [11] focused on theoretical frameworks for understanding gravity, but it may be limited in its practical applications. Yamamoto and Hayashi's article [12] used technical language and dealt with complex concepts that may be difficult for many readers to fully understand. Merdji and Zubairy's article [13] had limited scope and may not apply to more general systems. Gemmer, Mahler, and Winter's book [15] provided a comprehensive overview of the field but may be too technical for a general audience. Lastly, while Marvian and Spekkens' article [16] presents interesting theoretical results, it may have limited practical applications and is based on certain assumptions.One article by E. Bormashenko [17] deserves special mention. The author argues that the erasure of a bit of information necessarily leads to an increase in entropy and suggests that this principle can act as a steppingstone towards unifying various branches of physics. However, one of the possible contradictory statements of this article is the declaration of the identity of the nature of Einstein's laws and Landauer's principle, namely the identities of information-energy equivalence and mass-energy equivalence. This statement is doubtful because the energy required to erase one bit of information, which is proportional to temperature (kT), is not equivalent to the energy associated with mass.In this article, we explore the relationship between the E=m·c2 equation and the Landauer principle, and how these concepts relate to the physical properties of information. To avoid the potential backlash associated with insufficient explanation of the underlying physical justifications for the proposed formulas, it is important to thoroughly reason through and substantiate any claims made. While some may criticize the approach that links Einstein's formula to information without a deeper explanation, it is important to note that the importance of information in storage, transmission, and processing was not widely understood or appreciated until relatively recently.This task is challenging and requires a deep understanding of both formulas and their underlying principles. The upcoming chapter will explore the details of this task and the potential implications of a unified framework for our understanding of the physical universe.
2. Unifying Energy-Mass and Information-Energy Equivalences
- The proposed research examines the connections between Einstein's energy-mass equivalence and Landauer's information-energy equivalence using dimensional analysis. This method provides insights into the relationships between physical quantities and underlying principles, allowing for accurate equation verification and error detection.To make scientific progress, it is essential to analyze new ideas rigorously, considering complex phenomena. Oversimplification and neglecting important aspects hinder understanding and impede research. Utilizing up-to-date scientific data and validated findings from reputable journals is crucial for validating calculations and hypotheses. Rigor and precision are necessary to ensure the integrity and credibility of scientific advancements in this field.
2.1. The First Proposal
- In this study, we aim to integrate the Einstein formula (1) and the Landauer formula (2) by utilizing the dimensional analysis method, while considering any of its potential drawbacks. By conducting a thorough analysis of the physical implications of the formula and using dimensional analysis to explore their relationships, we can achieve a more profound understanding of the interdependence between energy, mass, and information:
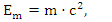 | (1) |
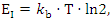 | (2) |
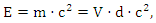 | (3) |
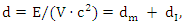 | (4) |
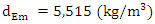 | (5) |
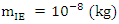 | (6) |
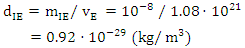 | (7) |
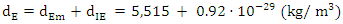 | (8) |
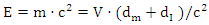 | (9) |
2.2. The Second Proposal
- Information overload is becoming an increasingly significant problem due to the growing amount of data being produced and stored. This chapter aims to provide a qualitative analysis of the challenges posed by this issue and explore potential solutions. The proposed formula combines Einstein's formula for energy and mass equivalence with Landauer's formula for information and energy equivalence. By equating the energy terms and solving for mass in terms of temperature and information, we get:
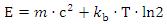 | (10) |
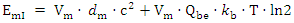 | (11) |
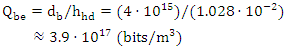 | (12) |
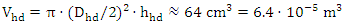 | (13) |
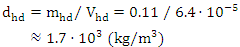 | (14) |
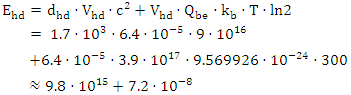 | (15) |
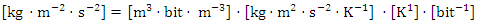 The equation (15) highlights a significant difference between its two components, with the first part being substantially larger than the second. However, it is essential to acknowledge that both equations (9) and (15) are theoretical and require empirical verification to establish their accuracy. Furthermore, a thorough understanding of each term's physical significance is crucial to apply them effectively. It is noteworthy that, in the present era, the mass of information is considered negligible in comparison to the mass connected to energy. Although these formulas demonstrate potential in various fields such as thermodynamics, information theory, and quantum mechanics, further research is necessary to fully comprehend their implications and limitations. Only then can we harness their potential and utilize them in practical applications.
The equation (15) highlights a significant difference between its two components, with the first part being substantially larger than the second. However, it is essential to acknowledge that both equations (9) and (15) are theoretical and require empirical verification to establish their accuracy. Furthermore, a thorough understanding of each term's physical significance is crucial to apply them effectively. It is noteworthy that, in the present era, the mass of information is considered negligible in comparison to the mass connected to energy. Although these formulas demonstrate potential in various fields such as thermodynamics, information theory, and quantum mechanics, further research is necessary to fully comprehend their implications and limitations. Only then can we harness their potential and utilize them in practical applications.3. Discussion
- The energy-mass equivalence formula, E=m·c², and the information-energy equivalence formula, ΔE=k·T·ln2, have significant implications for modern physics and information theory. These equations suggest a potential connection between energy, mass, and information, which has been explored in recent research. This connection implies that information has mass, and this has been experimentally confirmed in the fields of quantum mechanics and thermodynamics.The concept that information has mass suggests that the universe is richer in information than previously thought since the energy required to store information is proportional to its mass. This relationship has practical implications for future technologies, particularly in the development of quantum computing. A better understanding of how information is stored and processed at the quantum level may lead to more efficient and effective quantum computing systems.However, some scientists remain skeptical of the idea that the energy associated with erasing information is equivalent to a mass value since energy and mass are distinct concepts in physics. Despite this skepticism, the concept of information as a physical quantity is a fascinating area of research that could transform our understanding of physics and information theory, and open new possibilities for technological advancement [27,28].Quantitative calculations suggest that the "bit" concept can be applied to the technology used to store and process bits in digital devices, potentially affecting their performance. The connection between energy, mass, temperature, and information has practical implications for future technologies and could revolutionize the field of information technology.In summary, the concept that information has mass provides new insights into the fundamental nature of the universe and could lead to exciting breakthroughs in information technology. The relationship between energy, mass, and information is a fascinating topic that has generated considerable interest and discussion in the scientific community. Further research in this area could have far-reaching implications for our understanding of physics and the development of new technologies.
4. Conclusions
- The energy-mass equivalence formula and the information-energy equivalence formula proposed by Einstein and Landauer have had a significant impact on modern physics and information theory. Recent research has suggested a possible connection between these two equations based on the thermodynamic properties of information, which implies that information possesses mass.This relationship has potential implications for our understanding of the universe and the development of future technologies, such as quantum computing. The Landauer limit may also be a fundamental limit on the amount of information that can be processed by any physical system.Although this idea is still being explored and refined, it has the potential to transform our understanding of physics and information theory, leading to exciting breakthroughs in the field of information technology. Further research in this area could shed new light on a wide range of physical phenomena and provide new insights into the fundamental nature of the universe.
ACKNOWLEDGEMENTS
- Grateful for Prof. Mark Burgin's invaluable assistance in editing and preparing my article for publication. His expertise in mathematics, computer science, and information sciences has greatly contributed to its quality. May he rest in peace.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML