-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2021; 11(4): 71-77
doi:10.5923/j.ajcam.20211104.01
Received: Dec. 2, 2021; Accepted: Dec. 22, 2021; Published: Dec. 24, 2021

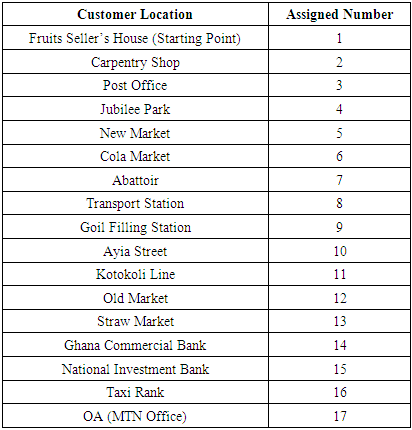
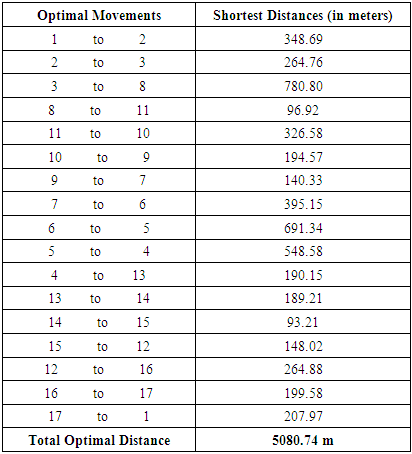
Analysis of the Operating Characteristics of Fruits’ Seller in Bolgatanga as a Travelling Salesperson Problem
Ahmed Salam Najat, Douglas Kwasi Boah
Department of Mathematics, C. K. Tedam University of Technology and Applied Sciences, Navrongo, Ghana
Correspondence to: Douglas Kwasi Boah, Department of Mathematics, C. K. Tedam University of Technology and Applied Sciences, Navrongo, Ghana.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

A travelling salesperson problem is where a salesperson starts from one place, visits all other required places once and returns to the initial point such that the overall covered distance is minimized. In this thesis, the concept of Travelling Salesperson Problem has been successfully used to analyze the operating characteristics of fruits’ seller in Bolgatanga in the Upper East Region of Ghana. The fruits’ seller was interviewed to find out the usual routes traversed by her to serve her scattered customers. Based on her responses, her daily routes and the various distances between each pair of customer locations were obtained from the Lands Commission in Bolgatanga in the Upper East Region of Ghana. A matrix of the shortest distances between pairs of customer locations in meters was then constructed and solved using Version 3 of TSP Solver and Generator which is based on the Branch and Bound Algorithm. The study has determined an optimal operating path for the fruits’ seller. It has also determined an optimal daily distance for the fruits’ seller. It is recommended that the fruits’ seller should always use the determined optimal operating path so as to minimize the total distance covered daily. Also, other hawkers should make conscious efforts to find out their optimal operating paths so as to minimize the total distances covered daily.
Keywords: Travelling Salesperson Problem, Fruits’ Seller, Optimal Operating Path, Optimal Daily Distance, Branch and Bound Algorithm, Customer Locations
Cite this paper: Ahmed Salam Najat, Douglas Kwasi Boah, Analysis of the Operating Characteristics of Fruits’ Seller in Bolgatanga as a Travelling Salesperson Problem, American Journal of Computational and Applied Mathematics , Vol. 11 No. 4, 2021, pp. 71-77. doi: 10.5923/j.ajcam.20211104.01.
Article Outline
1. Introduction
- The demands for fresh fruits such as pineapples, bananas, oranges, pawpaw and apples are very high in Bolgatanga in the Upper East Region of Ghana due to the immense health benefits these fruits have. Fresh fruits are either consumed raw or processed. A poor local consumer in Bolgatanga who cannot afford Don Simon, Kalippo, Bottled Fruit Juice etc. has to rely on fresh unprocessed fruits which are more natural as compared to the processed ones usually preserved with chemicals. From World Health Organization (WHO), vitamin C is critical for a well-functioning immune system and could play a vital role in the fight against COVID-19. Thus, maintaining a healthy diet by eating a variety of fresh fruits and vegetables helps boost the immune system against COVID-19 infections. According to Applegate et al [1], the Travelling Salesperson Problem also called the Travelling Salesman Problem (TSP) usually asks the question: “Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?” Droste [2] pointed out that the concept of a TSP is used for delivery, picking up children with school bus, order picking in warehouse and drilling holes in a printed circuit board. From delivery planning’s viewpoint, proper planning of routes and sequence of customer to serve could help in reducing travel distance, minimize cost and delivery time. According to Renaud et al [3], in numerous physical distribution problems, goods must be picked at an origin and delivered at a destination with precedence constraints between the customers to be visited. In fruits selling, the delivery of fruits is done by visiting individual customers at different parts of the city. Due to the high demand for fresh fruits, there is an increase in fruits vending in Bolgatanga which is a source of earnings for vendors to pay school fees, pay bills, feed children, pay rent etc. The local fresh fruits’ seller in Bolgatanga who buys her fruits in large quantity to sell has to go into hawking to reach her scattered customers who are in large numbers at different locations to prevent the fruits from staying long and going bad. After hawking on foot to reach her numerous customers, the seller becomes stressed out and sometimes has to either visit the hospital or rest which affects her business immensely. The study therefore sought to use the concept of Travelling Salesperson Problem to assist the fruits’ seller to find or determine the shortest possible routes to all her customers and serve them therefore reducing the total distance traversed by her every day.
2. Literature Review
- According to Hoffman [4], TSP has received ample attention of computer scientists and mathematicians precisely because it is not difficult to describe and not easy to solve. Applegate et al [1] argued that, “the origin of the name travelling salesman problem is a bit of a mystery”. It does not seem to be any authoritative or imposing documentation or certification pointing out the originator of the name, and there are no good conjectures as to when it first emanated into existence. However, one of the most influential or powerful initial TSP researchers was “Merrill Flood of Princeton University and the RAND Corporation”. Davendra [5] believed that “the TSP was first studied by Kalr Menger in Vienna and Harvard and the problem was later promoted by Hassler, Whitney & Merrill at Princeton”. Accordingly, Davendra [5] suggested that “the traveling salesman problem (TSP) was studied in the 18th century by a mathematician from Ireland named Sir William Rowam Hamilton and by the British mathematician named Thomas Penyngton Kirkman”. Historically, “Koopmans first became interested in the 48 States Problem of Hassler Whitney when the two of them were involved in the Princeton Surveys, as they attempted to solve the problem in connection with the work of Bob Singleton on school bus routing for the State of West Virginia”. Hitherto, what is not known is, “who created the peppier name “Traveling Salesman Problem” for Whitney’s problem, but that name certainly caught on, and the problem has turned out to be of very fundamental importance”. The concept of TSP has since received much attention. A number of papers in the theory and applications of TSP have been reported in the literature. Cerny [6] employed “a Monte Carlo algorithm to find approximate solutions of the traveling salesman problem”. The algorithm generated random permutations of stations of a traveling salesman trip, with probability depending on the length of the corresponding route and smaller banks respectively. Laporte [7] surveyed “the main known algorithms for the traveling salesman problem by focusing on a number of heuristics known to yield good TSP solutions in an empirical sense”. Renaud et al [3] dealt with “the pickup and delivery traveling salesman problem”. Firstly, they demonstrated how to adopt a number of classical or traditional traveling salesman heuristics to find a solution to the problem, and as a result proposed a novel and effective composite heuristic. Hoffman et al [4] presented “the concept of TSP and indicated how the prize collecting traveling salesman problem and the orienteering problem are special cases of the resource constrained TSP”. Bektas [8] presented an overview of formulations and solution procedures of the multiple traveling salesman problem. Basu and Ghosh [9] surveyed and presented that “Tabu search is one of the most widely applied metaheuristics for solving the TSP”. Korte [10] employed a cutting plane method which was combined alongside a branch-and-bound scheme with several destinations that could solve TSP scenarios optimally. Rajan [11] presented an innovative search algorithm motivated by the evolutionary optimization technique for the solution of TSP. Davendra [5] explored “a collection of research in the application of evolutionary algorithms and other optimal algorithms to solving the TSP”. Ahmed [12] examined “Genetic Algorithm for the Traveling Salesman Problem using Sequential Constructive Crossover Operator”. Adewole et al [13] presented a genetic algorithm with a local search algorithm which was employed to solve the TSP by generating a preset number of random tours and then improved the population until a stopping criterion was satisfied and the best chromosome which was a tour was returned as the solution. Barach et al [14] applied a Simulated Annealing algorithm to the Traveling Salesman Problem. Their study indicated that, the total tour length declines with temperature. Kumar et al [15] proposed that, genetic algorithm is one of the best methods used to solve various Travelling Salesman Problems (TSPs). Krishna et al [16] presented “an approach for solving traveling salesman problem based on improved ant colony algorithm and highlighted the Ant Colony Optimization (ACO) as a heuristic algorithm which has been proven as a successful technique applied to a number of combinatorial optimization problems”. Anshul and Devesh [17] presented “Bee Colony Optimization for solving the Travelling Salesman problem with its basic mechanism of bees foraging behavior and its efficiency in solving shortest path among various routes”. Saloni and Poonam [18] presented “Genetic algorithms which could find good solutions for the traveling salesman problem, though it depends very much on the way the problem is encoded and which crossover and mutation methods are used”. Sonam and Puneet [19] established “how Genetic Algorithm can be used to solve the Traveling Salesman Problem”. According to them, “Genetic Algorithm finds the good solution for the TSP, depending upon how the problem is encoded and which types of crossover and mutation methods are used”. Amos [20] conducted “a study which utilized Simulated Annealing to determine the optimal route for visiting all the regions in Ghana, save time and minimize expenditure”. He formulated “a real-life problem of Western African Examination Council (WAEC) as a TSP, modeled as network problem and a MATLAB program written using simulated annealing algorithm was used to solve the problem”. Lin et al [21] presented “an improved hybrid genetic algorithm to solve the two-dimensional Euclidean Traveling Salesman Problem, in which the crossover operator is enhanced with a local search”. Sakiyama and Arizono [22] developed “a new heuristic algorithm for solving TSP”. They claimed that “their proposed algorithm performed better in symmetric TSP and asymmetric TSP (time-dependent TSP) conditions compared with the NN algorithm using some TSP benchmark datasets from the TSPLIB”. Wedyan et al [23] presented “a nature-inspired optimization algorithm called the hydrological cycle algorithm (HCA) and used it to evaluate the TSP”. da Silva et al [24] presented “a novel mathematical approach for TSP which involved variable costs and priority prizes, whiles recognizing the client’s product and preference principles”. Ismail [25] studied and applied “a new constructive heuristics algorithm known as Domino Algorithm to the TSP”. Czopik [26] employed “the Hungarian algorithm for assignment problem to solve traveling salesman problem”. Three examples of application of the algorithm were provided. Danchick [27] presented an algorithm which accurately tackled the symmetric Traveling Salesman Problem (TSP). From the reviewed literature and to the best of our knowledge, application of the concept of Traveling Salesperson Problem to fruits’ seller in the manner presented in this paper appears non-existent. The study was therefore intended to fill that knowledge or research gap.
3. Materials and Methods
- The elementary traditional or classical model for the TSP can be stated as “an assignment problem with subtour elimination constraints”. Let n denote the number of cities; 𝑥𝑖𝑗, a binary decision variable which is equal to 1 if there is a travel from city i to city j, and 0 if not; and 𝑐𝑖𝑗, the cost of travel from city i to city j (Moustapha and Karwan [28]). The basic traditional formulation of the TSP is as follows:Minimize
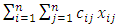 (Minimize total cost of tour)Subject to
(Minimize total cost of tour)Subject to 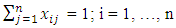 (Leave each city exactly once)
(Leave each city exactly once)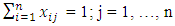 (Visit each city exactly once)
(Visit each city exactly once)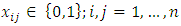
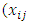 is a binary decision variable){(i, j):
is a binary decision variable){(i, j): 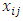 = 1, i, j = 2, …, n} (does not contain subtour)The maximum or total number of tours in an n-city problem is (n – 1)! (Taha [29]). For example, a 6-city problem will have (6 – 1)! = 5! = 120 tours. There are both exact and non-exact methods for solving TSPs. There exist two categories of the exact methods. One of them is by solving relaxation of the Linear Programming formulation of the TSP. It usually uses approaches like Interior Point Method, Cutting Plane Algorithm, Branch-and-Bound and Branch-and-Cut Method. The other category which is smaller is by means of Dynamic Programming. The main characteristic of both categories is a guarantee or assurance of obtaining optimal solutions regardless of space requirements and running time.Non-exact solutions offer possibly non-ideal regularly quicker solutions in a manner which contrarily compromises the exact or specific solution methods. Some of the non-exact solution methods for the TSP are Heuristics, Simulated Annealing, Tabu Search, Ant Colony Optimization and Genetic Algorithms. The exact method namely Branch and Bound Algorithm or Method was the main method used in the study. The notion or idea of the Branch and Bound Algorithm or Method is to commence or begin with the optimal solution of the associated assignment problem. If the solution is a tour, the process terminates or ends. Otherwise, restrictions are imposed on the resulting solution to disallow subtours. The idea is to create branches that assign a zero value to each of the variables of one of the subtours. Usually, the subtour with the smallest number of cities is selected for branching because it creates the smallest number of branches. If the solution of the assignment problem at any node is a tour, its objective value provides an upper bound on the optimum tour length. If it does not, further branching at the node is required. A subproblem is fathomed if it yields a smaller upper bound, or if there is evidence that it cannot lead to a better upper bound. The optimum tour is given at the node with the smallest upper bound. For a detailed discussion of Branch and Bound Algorithm or Methods for solving TSPs and TSP as a whole, the interested reader is referred to Sharma [30] and Taha [29].
= 1, i, j = 2, …, n} (does not contain subtour)The maximum or total number of tours in an n-city problem is (n – 1)! (Taha [29]). For example, a 6-city problem will have (6 – 1)! = 5! = 120 tours. There are both exact and non-exact methods for solving TSPs. There exist two categories of the exact methods. One of them is by solving relaxation of the Linear Programming formulation of the TSP. It usually uses approaches like Interior Point Method, Cutting Plane Algorithm, Branch-and-Bound and Branch-and-Cut Method. The other category which is smaller is by means of Dynamic Programming. The main characteristic of both categories is a guarantee or assurance of obtaining optimal solutions regardless of space requirements and running time.Non-exact solutions offer possibly non-ideal regularly quicker solutions in a manner which contrarily compromises the exact or specific solution methods. Some of the non-exact solution methods for the TSP are Heuristics, Simulated Annealing, Tabu Search, Ant Colony Optimization and Genetic Algorithms. The exact method namely Branch and Bound Algorithm or Method was the main method used in the study. The notion or idea of the Branch and Bound Algorithm or Method is to commence or begin with the optimal solution of the associated assignment problem. If the solution is a tour, the process terminates or ends. Otherwise, restrictions are imposed on the resulting solution to disallow subtours. The idea is to create branches that assign a zero value to each of the variables of one of the subtours. Usually, the subtour with the smallest number of cities is selected for branching because it creates the smallest number of branches. If the solution of the assignment problem at any node is a tour, its objective value provides an upper bound on the optimum tour length. If it does not, further branching at the node is required. A subproblem is fathomed if it yields a smaller upper bound, or if there is evidence that it cannot lead to a better upper bound. The optimum tour is given at the node with the smallest upper bound. For a detailed discussion of Branch and Bound Algorithm or Methods for solving TSPs and TSP as a whole, the interested reader is referred to Sharma [30] and Taha [29]. 4. Results and Discussions
- The fruits’ seller was interviewed to find out the usual routes traversed by her to serve her scattered customers. Based on her responses, Figure 1 which shows her daily routes and the various distances between each pair of customer locations was obtained from the Lands Commission in Bolgatanga in the Upper East Region of Ghana.The various customer locations of the fruits’ seller were then arranged and numbered as given in Table 1.
|
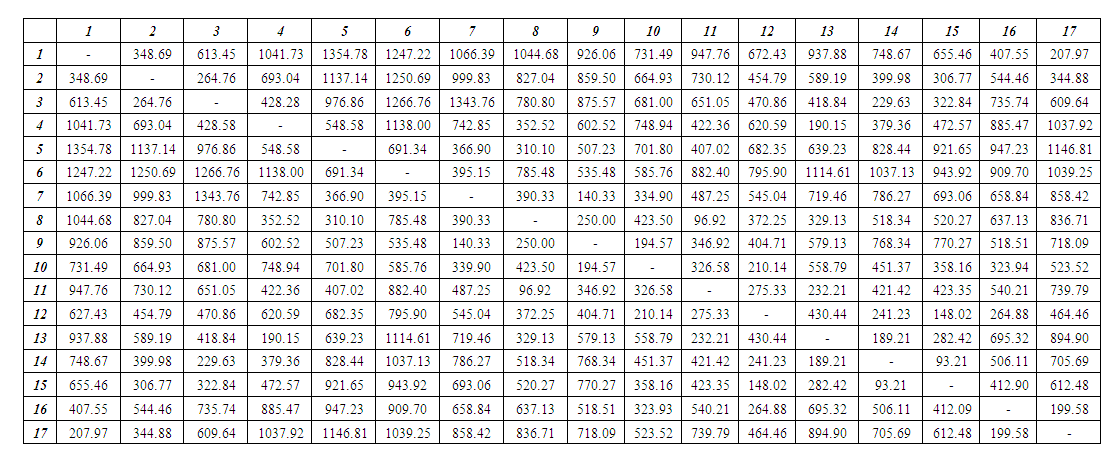 | Table 2. A matrix of the shortest distances between pairs of customer locations in meters |
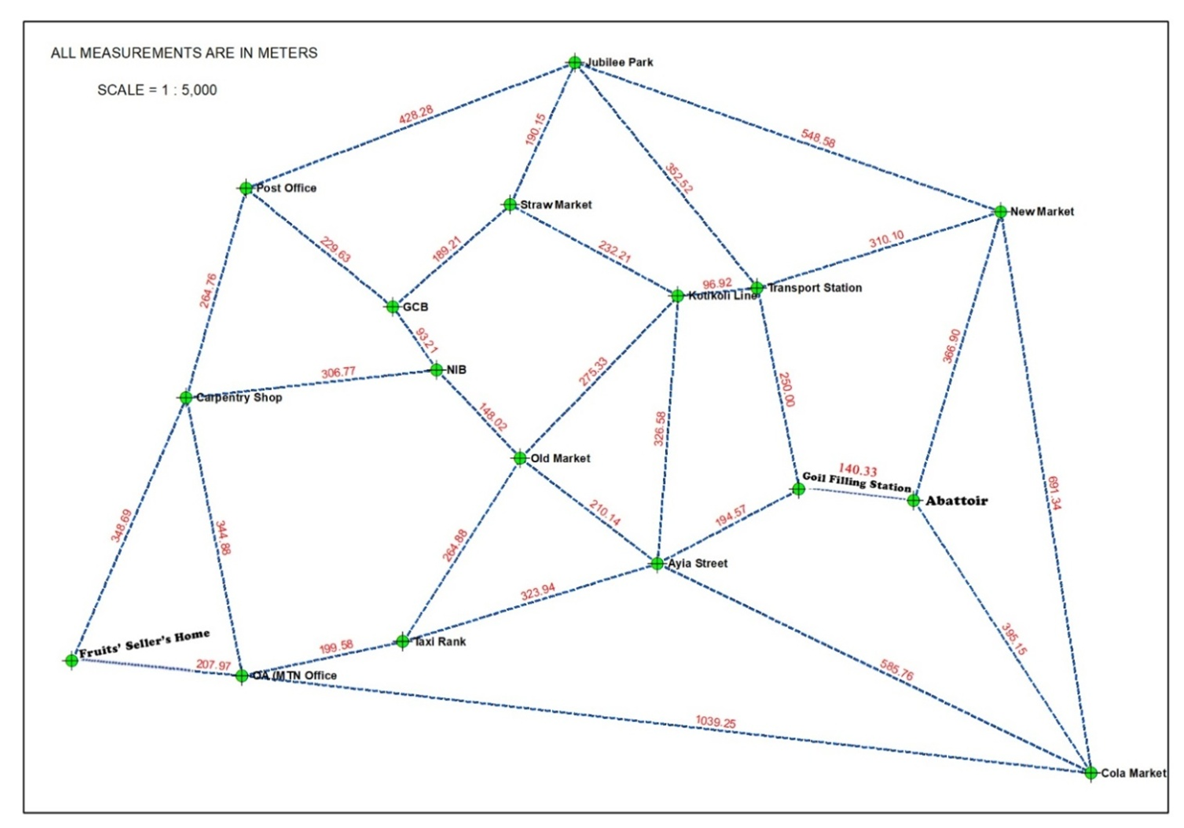 | Figure 1. Daily routes of the fruits’ seller and distances between pairs of customer locations in meters |
 Carpentry shop
Carpentry shop  Post office
Post office  Jubilee park
Jubilee park  Straw market
Straw market  GCB
GCB  NIB
NIB  Old market
Old market  Taxi rank
Taxi rank  Ayia street
Ayia street  Kotokoli line
Kotokoli line  Transport station
Transport station  Goil filling station
Goil filling station  Abattoir
Abattoir  New market
New market  Cola market
Cola market  OA MTN office
OA MTN office  Fruits seller’s house with their corresponding distances being 348.69 + 264.76 + 428.28 + 190.15 + 189.21 + 93.21 + 148.02 + 264.88 + 323.94 + 326.58 + 96.92 + 250.00 + 140.38 + 366.90 + 3691.34 + 1039.25 + 207.97 = 5370.48 m.Route 2Fruits seller’s house
Fruits seller’s house with their corresponding distances being 348.69 + 264.76 + 428.28 + 190.15 + 189.21 + 93.21 + 148.02 + 264.88 + 323.94 + 326.58 + 96.92 + 250.00 + 140.38 + 366.90 + 3691.34 + 1039.25 + 207.97 = 5370.48 m.Route 2Fruits seller’s house  OA MTN Office
OA MTN Office  Cola market
Cola market  Abattoir
Abattoir  New market
New market  Jubilee park
Jubilee park  Straw market
Straw market  Kotokoli line
Kotokoli line  Transport station
Transport station  Goil filling station
Goil filling station  Ayia street
Ayia street  Taxi rank
Taxi rank  Old market
Old market  NIB
NIB GCB
GCB  Post office
Post office  Carpentry shop
Carpentry shop  Fruits seller’s house with their corresponding distances being 207.97 + 1039.25 + 395.15 + 366.90 + 548.58 + 190.15 + 232.21 + 96.92 + 250.00 + 194.57 + 323.94 + 264.88 + 148.02 + 93.21 + 229.63 + 348.69 = 5194.83 m.Route 3Fruits seller’s house
Fruits seller’s house with their corresponding distances being 207.97 + 1039.25 + 395.15 + 366.90 + 548.58 + 190.15 + 232.21 + 96.92 + 250.00 + 194.57 + 323.94 + 264.88 + 148.02 + 93.21 + 229.63 + 348.69 = 5194.83 m.Route 3Fruits seller’s house  Carpentry shop
Carpentry shop  NIB
NIB  GCB
GCB  Post office
Post office  Jubilee park
Jubilee park  Straw market
Straw market  Kotokoli line
Kotokoli line  Old market
Old market  Taxi rank
Taxi rank  Ayia street
Ayia street  Goil filling station
Goil filling station  Transport station
Transport station  New market
New market  Abattoir
Abattoir  Cola market
Cola market  OA MTN office
OA MTN office  Fruits seller’s house with their corresponding distances being 348.69 + 306.77 + 93.21 + 229.63 + 428.28 + 190.15 + 232.21 + 275.33 + 264.88 + 323.94 + 194.57 + 250.00 + 310.10 + 366.90 + 395.15 + 1039.25 + 207.97 = 5457 m.Route 4Fruits seller’s house
Fruits seller’s house with their corresponding distances being 348.69 + 306.77 + 93.21 + 229.63 + 428.28 + 190.15 + 232.21 + 275.33 + 264.88 + 323.94 + 194.57 + 250.00 + 310.10 + 366.90 + 395.15 + 1039.25 + 207.97 = 5457 m.Route 4Fruits seller’s house  OA MTN Office
OA MTN Office  Cola market
Cola market  New market
New market  Abattoir
Abattoir  Goil filling station
Goil filling station  Transport station
Transport station  Jubilee park
Jubilee park  Straw market
Straw market  Kotokoli line
Kotokoli line  Ayia street
Ayia street  Taxi rank
Taxi rank  Old market
Old market  NIB
NIB  GCB
GCB  Post office
Post office  Carpentry shop
Carpentry shop  Fruits seller’s house with their corresponding distances being 207.97 + 1039.25 + 691.34 + 366.90 + 140.30 + 250.00 + 352.52 + 190.15 + 232.21 + 326.58 + 323.94 + 264.88 + 148.02 + 93.21 + 229.63 + 264.76 + 348.69 = 5470.33 m.Route 5Fruits seller’s house
Fruits seller’s house with their corresponding distances being 207.97 + 1039.25 + 691.34 + 366.90 + 140.30 + 250.00 + 352.52 + 190.15 + 232.21 + 326.58 + 323.94 + 264.88 + 148.02 + 93.21 + 229.63 + 264.76 + 348.69 = 5470.33 m.Route 5Fruits seller’s house  Carpentry shop
Carpentry shop  NIB
NIB  GCB
GCB  Post office
Post office  Jubilee park
Jubilee park  Straw market
Straw market  Kotokoli line
Kotokoli line  Old market
Old market  Taxi rank
Taxi rank  Ayia street
Ayia street  Goil filling station
Goil filling station  Transport station
Transport station  New market
New market  Abattoir
Abattoir  Cola market
Cola market  OA MTN office
OA MTN office  Fruits seller’s house with their corresponding distances being 348.69 + 306.77 + 691.34 + 93.21 + 229.63 + 428.28 + 190.15 + 232.21 + 275.33 + 264.88 + 323.94 + 194.57 + 250.00 + 310.10 + 366.90 + 395.15 + 1039.25 + 207.03 = 5457.03 m.Optimality AnalysisIt should be recalled that, the maximum number of tours in an ‘n’ city situation is (n - 1)! In the case of this work, the total number of tours will be (17-1)! = 16! = 20922789888000. It was therefore practically impossible to determine all these numerous numbers of tours and pick the optimal tour out of them. Version 3 of TSP Solver and Generator developed by Serdiuk [31] which is based on the Branch and Bound Algorithm was then used to solve the problem presented in Table 2. The optimal solution is as given in Table 3.
Fruits seller’s house with their corresponding distances being 348.69 + 306.77 + 691.34 + 93.21 + 229.63 + 428.28 + 190.15 + 232.21 + 275.33 + 264.88 + 323.94 + 194.57 + 250.00 + 310.10 + 366.90 + 395.15 + 1039.25 + 207.03 = 5457.03 m.Optimality AnalysisIt should be recalled that, the maximum number of tours in an ‘n’ city situation is (n - 1)! In the case of this work, the total number of tours will be (17-1)! = 16! = 20922789888000. It was therefore practically impossible to determine all these numerous numbers of tours and pick the optimal tour out of them. Version 3 of TSP Solver and Generator developed by Serdiuk [31] which is based on the Branch and Bound Algorithm was then used to solve the problem presented in Table 2. The optimal solution is as given in Table 3.
|
 2
2  3
3  8
8  11
11  10
10  9
9  7
7  6
6  5
5  4
4  13
13 14
14  15
15  12
12  16
16  17
17  1.The results can be interpreted as follows:Fruits Seller’s House (Starting Point)
1.The results can be interpreted as follows:Fruits Seller’s House (Starting Point)  Carpentry Shop
Carpentry Shop  Post Office
Post Office  Transport Station
Transport Station  Kotokoli Line
Kotokoli Line  Ayia Street
Ayia Street  Goil Filling Station
Goil Filling Station  Abattoir
Abattoir  Cola Market
Cola Market  New Market
New Market  Jubilee Park
Jubilee Park  Straw Market
Straw Market  Ghana Commercial Bank
Ghana Commercial Bank  National Investment Bank
National Investment Bank  Old Market
Old Market  Taxi Rank
Taxi Rank  OA (MTN Office)
OA (MTN Office)  Fruits Seller’s House (Starting Point) with an optimal distance of 5080.74m. The constructed network of the daily movements of the fruits’ seller can easily tell anyone the places visited daily by the fruits’ seller. This means that, one will not have struggle to know the daily movements of the fruits’ seller. The determined optimal operating paths for the fruits’ seller will help her to reduce or minimize the total distance traversed daily. This will in effect reduce the stress the fruits seller used to go through daily in serving her scattered customers. Bodily pains and for that matter hospital bills or income spent on drugs and medication will reduce drastically. Finally, the determined optimal daily distance for the fruits’ seller can easily tell anyone the total distance that should be covered daily by the fruits’ seller.
Fruits Seller’s House (Starting Point) with an optimal distance of 5080.74m. The constructed network of the daily movements of the fruits’ seller can easily tell anyone the places visited daily by the fruits’ seller. This means that, one will not have struggle to know the daily movements of the fruits’ seller. The determined optimal operating paths for the fruits’ seller will help her to reduce or minimize the total distance traversed daily. This will in effect reduce the stress the fruits seller used to go through daily in serving her scattered customers. Bodily pains and for that matter hospital bills or income spent on drugs and medication will reduce drastically. Finally, the determined optimal daily distance for the fruits’ seller can easily tell anyone the total distance that should be covered daily by the fruits’ seller. 5. Conclusions
- The concept of Travelling Salesperson Problem has been successfully used to analyze the operating characteristics of fruits’ seller in Bolgatanga in the Upper East Region of Ghana. Specifically, the study has successfully constructed a network of the daily movements of the fruits’ seller; determined an optimal operating path for the fruits’ seller and finally determined an optimal daily distance for the fruits’ seller.The study recommends that the fruits’ seller should always use the determined optimal operating path in order to minimize the total distance covered daily. Also, other hawkers should make conscious efforts to find out their optimal operating paths so as to minimize their total distances covered daily.The study has contributed significantly to knowledge by providing a scientific way by which hawkers can operate. Also, the study has filled the knowledge or research gap of application of the concept of TSP to fruits’ seller or hawker in the manner presented in this paper which appeared non-existent.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML