R. Thukral
Padé Research Centre, 39 Deanswood Hill, Leeds, West Yorkshire, LS17 5JS, England
Correspondence to: R. Thukral, Padé Research Centre, 39 Deanswood Hill, Leeds, West Yorkshire, LS17 5JS, England.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this paper we propose two four-point secant-type methods for finding simple root of nonlinear equations. The new iterative methods do not require any derivatives and has a convergence order of 1.92. Also, we have proved the convergence order of the new methods which require only one function evaluations per full iteration. In addition, numerical examples demonstrate exceptional convergence speed of the proposed methods. It is observed that the new four-point secant-type iterative methods are very effective and robust.
Keywords:
Secant-type methods, Simple root, Nonlinear equations, Root-finding, Order of convergence
Cite this paper: R. Thukral, Further Improvement of Secant-Type Methods for Solving Nonlinear Equations, American Journal of Computational and Applied Mathematics , Vol. 11 No. 3, 2021, pp. 60-64. doi: 10.5923/j.ajcam.20211103.02.
1. Introduction
The root-finding problem arises in a wide variety of practical applications in science and engineering [1,2,7]. In this paper, we propose two four-point secant-type iterative methods to find a simple root of the nonlinear equation. It is well established that the multipoint root-solvers are of great practical importance since it overcomes theoretical limits of one-point methods concerning the convergence order and computational efficiency. Recently, some modifications of the secant-type methods for simple root have been proposed and analysed [3-5]. Hence, the purpose of this paper is to show further development of the secant-type methods. The four-point secant-type iterative methods are shown to have a better order of convergence then the similar secant-type methods considered in this paper. We have found that the efficiency index of new iterative methods has a better efficiency index than the classical Newton method.We consider the classical secant iterative method for finding simple root of nonlinear equations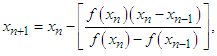 | (1) |
and the order of convergence is 1.62. For the purpose of this paper, we present two new four-point secant-type methods for finding simple root of nonlinear equations.The paper is organized as follows: Some essential definitions relevant to the present work are stated in the section 2. In section 3 we define two four-point secant-type methods and prove their order of convergence. In section 4, well-established three-point methods are stated, which will demonstrate the effectiveness of the new four-point iterative methods. Finally, in section 5, numerical comparisons are made to demonstrate the performance of the presented methods.
2. Review of Definitions
In order to establish the order of convergence of an iterative method, following definitions are used [1-5,7].Definition 1 Let 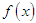 be a real-valued function with a root
be a real-valued function with a root 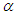 and let
and let 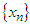 be a sequence of real numbers that converge towards
be a sequence of real numbers that converge towards 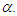 The order of convergence p is given by
The order of convergence p is given by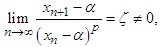 | (2) |
where 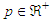 and
and 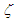 is the asymptotic error constant.Definition 2 Let
is the asymptotic error constant.Definition 2 Let 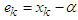 be the error in the kth iteration, then the relation
be the error in the kth iteration, then the relation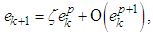 | (3) |
is the error equation. If the error equation exists, then p is the order of convergence of the iterative method.Definition 3 Let r be the number of function evaluations of the method. The efficiency of the method is measured by the concept of efficiency index and defined as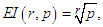 | (4) |
where p is the order of convergence of the method.Definition 4 Suppose that 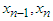 and
and 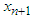 are three successive iterations closer to the root
are three successive iterations closer to the root 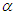 of a nonlinear equation. Then the computational order of convergence [8] may be approximated by
of a nonlinear equation. Then the computational order of convergence [8] may be approximated by 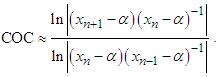 | (5) |
3. Development of the Methods and Convergence Analysis
In this section, we define two four-point secant-type iterative methods. The following approximation terms are used in the methods to calculate the simple root of the nonlinear equation; 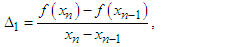 | (6) |
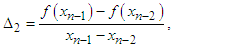 | (7) |
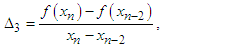 | (8) |
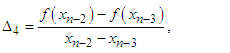 | (9) |
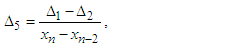 | (10) |
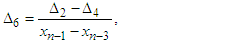 | (11) |
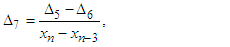 | (12) |
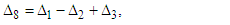 | (13) |
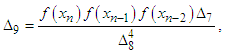 | (14) |
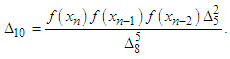 | (15) |
The two of the four-point secant-type methods have convergence order of 1.92 and they are expressed as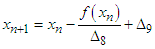 | (16) |
and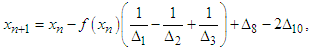 | (17) |
where 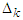 are given above,
are given above, 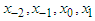 are the initial values and provided that the denominators of (16) and (17) are not equal to zero. It is essential to verify our finding and prove the order of convergence of the new four-point secant-type iterative methods.Theorem 1Let
are the initial values and provided that the denominators of (16) and (17) are not equal to zero. It is essential to verify our finding and prove the order of convergence of the new four-point secant-type iterative methods.Theorem 1Let 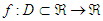 be a sufficiently differentiable function and let for an open interval D has
be a sufficiently differentiable function and let for an open interval D has 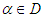 be a simple zero of
be a simple zero of 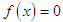 in an open interval D, with
in an open interval D, with 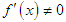 in D. If the initial points
in D. If the initial points 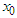 and
and 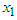 are sufficiently close to
are sufficiently close to 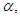 then the asymptotic convergence order of the new methods defined by (16) is 1.92.Proof Let
then the asymptotic convergence order of the new methods defined by (16) is 1.92.Proof Let 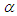 be a simple root of
be a simple root of 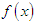 , i.e.
, i.e. 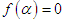 and
and 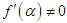 , and the errors at
, and the errors at 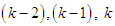 and
and 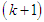 iteration are expressed as
iteration are expressed as 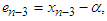
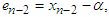
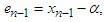
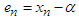 and
and 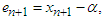 respectively.Using Taylor expansion and taking into account that
respectively.Using Taylor expansion and taking into account that 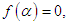 we have
we have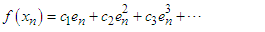 | (18) |
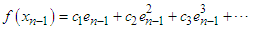 | (19) |
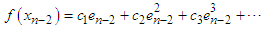 | (20) |
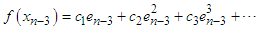 | (21) |
where 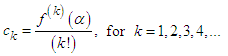 | (22) |
Using (18)-(21), we obtain 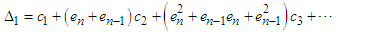 | (23) |
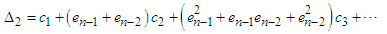 | (24) |
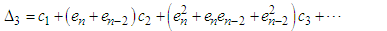 | (25) |
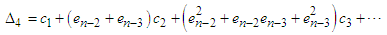 | (26) |
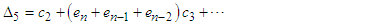 | (27) |
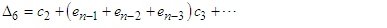 | (28) |
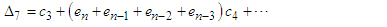 | (29) |
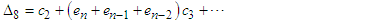 | (30) |
 | (29) |
 | (30) |
Substituting the expressions (18)-(30) in (16), we obtain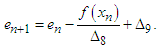 | (31) |
Simplifying, we obtain the error equation for the new four-point secant-type iterative method, given by (16) is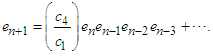 | (32) |
In order to prove the order of convergence of (16) and we defining positive real terms of 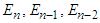 and
and 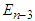 as
as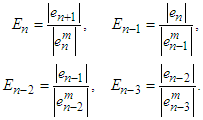 | (33) |
The error terms of 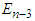 are given as
are given as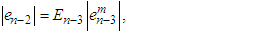 | (34) |
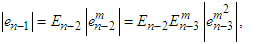 | (35) |
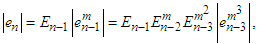 | (36) |
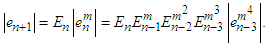 | (37) |
It is obtained from (30) that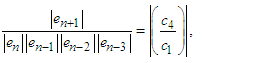 | (38) |
substituting the appropriate expressions of errors terms in (37), we get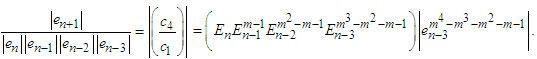 | (39) |
In order to satisfy the asymptotic equation (36), the power of the error term shall approach zero, that is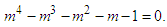 | (40) |
The roots of the fourth-order equation (40) are;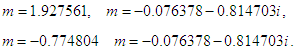 | (41) |
The order of convergence of the new four-point secant-type method is determined by the positive root of (41). Hence, the new four-point secant-type method defined by (16) has a convergence order of 1.92. This completes the proof. We repeat the procedure to prove the error equations for the other proposed three-point secant-type methods. Again, the order of convergence of the other four-point secant-type methods is determined by the positive root of (41). Hence, the new four-point secant-type methods defined by (12) has a convergence order of 1.92.RemarkThe new four-point secant-type iterative methods require single function evaluation and has the order of convergence 1.92. To determine the efficiency index of these new methods, definition 3 shall be used, hence, the efficiency index of the new four-point secant-type iterative methods is same as the order of convergence.
4. The Established Methods
For the purpose of comparison, three particular well-established iterative methods [5-7] are considered and they are given below,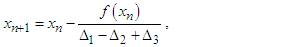 | (42) |
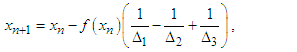 | (43) |
and the Tiruneh et al method [6], given by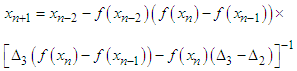 | (44) |
The three-point secant-type methods defined by (42)-(44) has a convergence order of 1.84.
5. Application Examples
The proposed four-point secant-type iterative methods are employed to solve nonlinear equation with simple root. The difference between the simple root 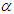 and the approximation
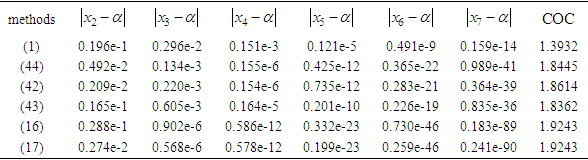
and the approximation 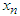 for test function with four appropriate initial points and are displayed in tables. Furthermore, the computational order of convergence approximations is displayed in tables and we observe that this perfectly coincides with the theoretical result. The numerical computations listed in the table was performed on an algebraic system called Maple and the errors displayed are of absolute value.Numerical example 1We will demonstrate the order of convergence of the new four-point secant-type iterative methods for the following nonlinear equation
for test function with four appropriate initial points and are displayed in tables. Furthermore, the computational order of convergence approximations is displayed in tables and we observe that this perfectly coincides with the theoretical result. The numerical computations listed in the table was performed on an algebraic system called Maple and the errors displayed are of absolute value.Numerical example 1We will demonstrate the order of convergence of the new four-point secant-type iterative methods for the following nonlinear equation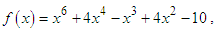 | (45) |
having the exact value of the simple root of (45) is 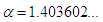 In Table 1 the errors obtained by the methods described are based on the initial points
In Table 1 the errors obtained by the methods described are based on the initial points 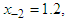
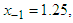
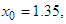
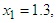
Table 1. Errors occurring in the approximation of the simple root of (45)
 |
| |
|
Numerical example 2We will demonstrate the order of convergence of the new four-point secant-type iterative methods for the following nonlinear equation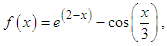 | (46) |
having exact value of the simple root of (46) is 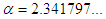 In Table 2 the errors obtained by the methods described are based on the initial points
In Table 2 the errors obtained by the methods described are based on the initial points 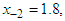
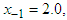
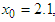
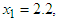
Table 2. Errors occurring in the approximation of the simple root of (46)
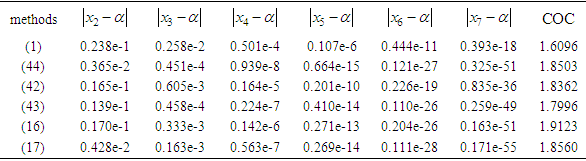 |
| |
|
Numerical example 3We will demonstrate the order of convergence of the new four-point secant-type iterative methods for the following nonlinear equation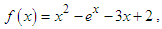 | (47) |
having exact value of the simple root of (47) is 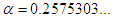 In Table 3 the errors obtained by the methods described are based on the initial guess
In Table 3 the errors obtained by the methods described are based on the initial guess 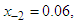
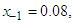
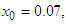
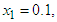
Table 3. Errors occurring in the approximation of the simple root of (47)
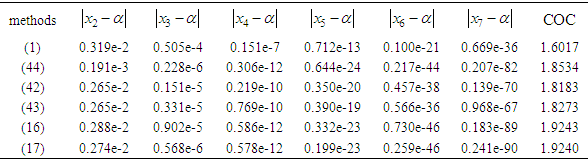 |
| |
|
6. Conclusions
Two new four-point secant-type methods for solving nonlinear equations with simple root have been presented. The effectiveness of the new iterative methods is examined by showing the accuracy of the simple root of several nonlinear equations. Convergence analysis proves that the new four-point iterative methods preserve their order of convergence. Numerical examples are provided to support the theoretical results obtained and compared with different methods. The major advantages of the new four-point secant-type methods are that they are very effective and produces high precision of approximation of the simple root and they are derivative-free. Finally, we conclude that the new four-point secant-type iterative methods may be considered a very good alternative to the established methods.
References
| [1] | A. M. Ostrowski, Solutions of equations and system of equations, Academic Press, New York, 1960. |
| [2] | M. S. Petkovic, B. Neta, L. D. Petkovic, J. Dzunic, Multipoint methods for solving nonlinear equations, Elsevier 2012. |
| [3] | R. Thukral, A new secant-type method for solving nonlinear equations, Amer. J. Comput. Appl. Math. 8 (2) (2018) 32-36. |
| [4] | R. Thukral, Further development of secant-type methods for solving nonlinear equations, Inter. J. Adv. J. Math. 38 (5) (2018) 45-53. |
| [5] | R. Thukral, New three-point secant-type methods for solving nonlinear equations, Amer. J. Comput. Appl. Math. 10 (1) (2020) 15-20. |
| [6] | A.T. Tiruneh, T. Y. Debessai, G. C. Bwembya, S. J. Nkambule, A modified three-point secant method with improved rate and characteristics of convergence, Inter. J. Adv. Math. (4) (2019) 69-83. |
| [7] | J. F. Traub, Iterative Methods for solution of equations, Chelsea publishing company, New York 1977. |
| [8] | S. Weerakoon, T. G. I. Fernando, A variant of Newton’s method with accelerated third-order convergence, Appl. Math. Lett. 13 (2000) 87-93. |


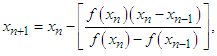
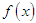 be a real-valued function with a root
be a real-valued function with a root 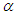 and let
and let 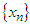 be a sequence of real numbers that converge towards
be a sequence of real numbers that converge towards 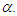 The order of convergence p is given by
The order of convergence p is given by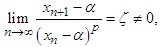
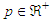 and
and 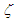 is the asymptotic error constant.Definition 2 Let
is the asymptotic error constant.Definition 2 Let 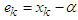 be the error in the kth iteration, then the relation
be the error in the kth iteration, then the relation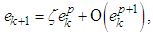
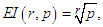
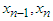 and
and 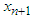 are three successive iterations closer to the root
are three successive iterations closer to the root 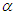 of a nonlinear equation. Then the computational order of convergence [8] may be approximated by
of a nonlinear equation. Then the computational order of convergence [8] may be approximated by 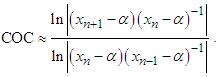
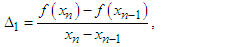
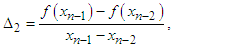
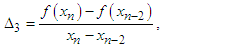
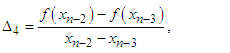
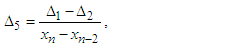
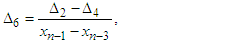
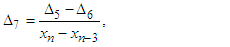
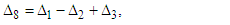
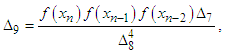
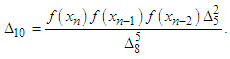
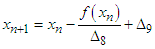
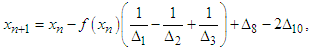
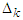 are given above,
are given above, 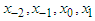 are the initial values and provided that the denominators of (16) and (17) are not equal to zero. It is essential to verify our finding and prove the order of convergence of the new four-point secant-type iterative methods.Theorem 1Let
are the initial values and provided that the denominators of (16) and (17) are not equal to zero. It is essential to verify our finding and prove the order of convergence of the new four-point secant-type iterative methods.Theorem 1Let 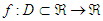 be a sufficiently differentiable function and let for an open interval D has
be a sufficiently differentiable function and let for an open interval D has 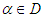 be a simple zero of
be a simple zero of 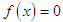 in an open interval D, with
in an open interval D, with 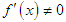 in D. If the initial points
in D. If the initial points 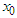 and
and 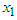 are sufficiently close to
are sufficiently close to 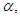 then the asymptotic convergence order of the new methods defined by (16) is 1.92.Proof Let
then the asymptotic convergence order of the new methods defined by (16) is 1.92.Proof Let 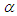 be a simple root of
be a simple root of 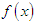 , i.e.
, i.e. 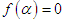 and
and 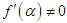 , and the errors at
, and the errors at 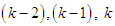 and
and 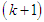 iteration are expressed as
iteration are expressed as 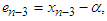
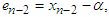
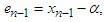
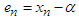 and
and 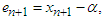 respectively.Using Taylor expansion and taking into account that
respectively.Using Taylor expansion and taking into account that 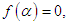 we have
we have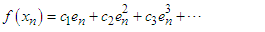
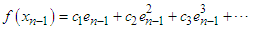
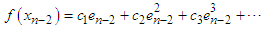
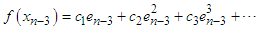
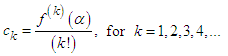
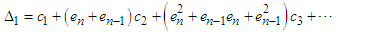
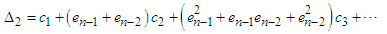
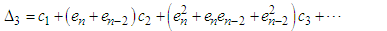
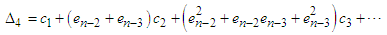
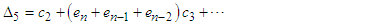
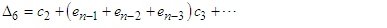
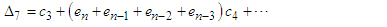
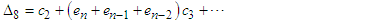


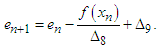
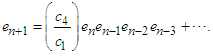
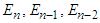 and
and 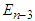 as
as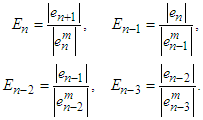
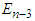 are given as
are given as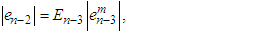
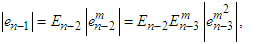
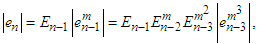
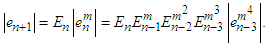
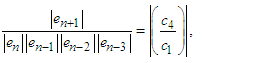
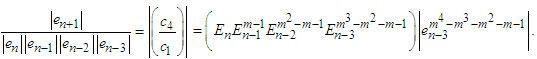
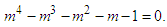
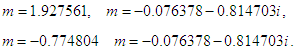
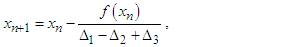
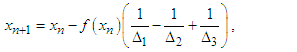
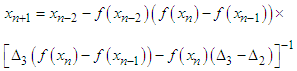
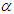 and the approximation
and the approximation 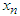 for test function with four appropriate initial points and are displayed in tables. Furthermore, the computational order of convergence approximations is displayed in tables and we observe that this perfectly coincides with the theoretical result. The numerical computations listed in the table was performed on an algebraic system called Maple and the errors displayed are of absolute value.Numerical example 1We will demonstrate the order of convergence of the new four-point secant-type iterative methods for the following nonlinear equation
for test function with four appropriate initial points and are displayed in tables. Furthermore, the computational order of convergence approximations is displayed in tables and we observe that this perfectly coincides with the theoretical result. The numerical computations listed in the table was performed on an algebraic system called Maple and the errors displayed are of absolute value.Numerical example 1We will demonstrate the order of convergence of the new four-point secant-type iterative methods for the following nonlinear equation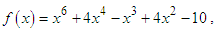
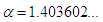 In Table 1 the errors obtained by the methods described are based on the initial points
In Table 1 the errors obtained by the methods described are based on the initial points 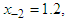
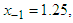
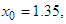
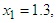
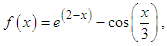
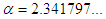 In Table 2 the errors obtained by the methods described are based on the initial points
In Table 2 the errors obtained by the methods described are based on the initial points 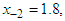
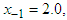
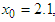
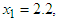
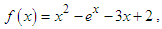
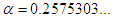 In Table 3 the errors obtained by the methods described are based on the initial guess
In Table 3 the errors obtained by the methods described are based on the initial guess 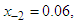
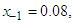
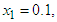
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML

