Mečislovas Mariūnas
Department of Biomechanical Engineering, Vilnius Gediminas Technical University, Vilnius LT, Lithuania
Correspondence to: Mečislovas Mariūnas, Department of Biomechanical Engineering, Vilnius Gediminas Technical University, Vilnius LT, Lithuania.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
This paper presents a method for determining vibration damping in a nonlinear dynamic system of one degree of freedom. It has been found that in the case of resonance, the vibrations of the dynamic system are damped not only by the force generated by the external excitation vibration velocity, but also by the forces generated by the displacements, velocities and accelerations of vibrations at other frequencies. It was found that the magnitude of the amplitude varies in the interval of one excitation cycle and the magnitude and regularity of its change depend on the ratio of resonant, parametric vibrations and external excitation force frequencies. It has been determined that the forces generated by a nonlinear dynamic system can be vibration-exciting forces at one time and vibration-damping forces at another. Studies have found that even in the case of resonances in a nonlinear dynamic system, the vibrations are damped severel hundred time more than in a linear dynamic system. Analytical methods have been developed to allow quadratic and cubic dynamic systems of nonlinearity to choose parameter values during design that would increase the damping of the system and reduce the vibration level of the developed system and ensure its safe operation. The certainty of the analytical methods presented in the article was verified by numerical calculations.
Keywords:
Vibration damping, Excitation forces, Nonlinear dynamic system, Quadratic and cubic order nonlinearities, Vibration, Resonant and parametric frequencies, One degree of freedom
Cite this paper: Mečislovas Mariūnas, Vibration Damping Study in a Nonlinear Dynamical System of One Degree of Freedom, American Journal of Computational and Applied Mathematics , Vol. 11 No. 2, 2021, pp. 30-41. doi: 10.5923/j.ajcam.20211102.02.
1. Introduction
The process by which vibration steadily diminishes in amplitude is called damping, where the energy of the vibrating system is dissipated by various mechanisms [1]. Many different models are used to evaluate damping in dynamic systems [1-13]. When designing nonlinear dynamic systems, it is very important to be able to evaluate the damping properties and possibly change their size during the process. In the analysis of damping in a dynamic system, in many mathematical models the damping forces are related to the movements of the degrees of freedom of the system [1-13]. Viscous damping is a popular model that relates the damping force to velocity by a linear function, with a factor known as the damping coefficient. Despite its simplicity, viscous damping is not satisfactory for solid materials. Practical observations of solid structural and mechanical systems, however, suggest a clear lack of systematic dependence of energy dissipation on frequency [1]. In the works [2-4] the parameters of elastic systems are analyzed, their nonlinearity properties are evaluated and approximate mathematical models of damping are created. According to hysteresis loops of the clamp obtained from experimental test, the simplified bilinear stiffness and damping model is proposed. Then the Finite Element (FE) model of L-type pipeline system with clamps is established using Timoshenko beam theory in combination with aforementioned stiffness-damping model [3]. Both hammering and shaker tests verify the FE model via the comparisons of natural frequencies and vibration responses. The natural frequencies and vibration responses obtained from the established finite element model are verified by experimental tests. In [7], a new nonparametric and output-only identification procedure for nonlinear damping is studied. By introducing the concept of the stochastic state space, they formulate a stochastic inverse problem for a nonlinear damping. The solution of the stochastic inverse problem is designed as probabilistic expression via the hierarchical Bayesian formulation by considering various uncertainties such as the information insufficiency in parameter of interests or errors in measurement. The probability space is estimated using Markov chain Monte Carlo. The applicability of the proposed method is demonstrated through numerical experiment and particular application to a realistic problem related to ship roll motion. In [8], the analysis of nonlinear dynamic systems is simplified by the fact that they show no jump or bifurcation behavior, and indeed can often be well represented by an equivalent linear system, whose damping parameters depend on the form and amplitude of the excitation, in a “quasi-linear” model. For simplicity, it is assumed that the system is stable and that the nonlinear damping force depends on the nth power of the velocity. For sinusoidal excitation, it is shown that the response is often also almost sinusoidal, and methods for calculating the amplitude are described based on the harmonic balance method, which is closely related to the describing function method used in control engineering. For random excitation, several methods of analysis are shown to be equivalent. In general, iterative methods need to be used for calculating the equivalent linear damper, since its value depends on the system’s response, which itself depends on the value of the equivalent linear damper. The power dissipation of the equivalent linear damper, for both sinusoidal and random cases, matches that dissipated by the nonlinear damper, providing both a firm theoretical basis for this modeling approach and clear physical insight. The efficiency of the proposed vibration isolation strategy is numerically demonstrated over the original device. The authors of the paper [10] solved the problems of vibration damping by creating a nonlinear dynamic vibration damper with appropriately selected parameters based on the geometry of the overlap truss. In [11], the author examines nonlinear damping from the viscoelasticity by using a single-degre-of freedom model obtained from standard linear solid material where geometric nonlinearity is inserted in. The solution of the problem is initially reached by a third-order harmonic balance method. Then, the equation of motion is obtained in differential form, which is extremely useful in applications. In [12], the authors solve the problem of vibration damping by using a system with negative dynamic stiffness. Articles [5], [6], [8], etc. also use approximate analytical or numerical methods to evaluate vibration damping in nonlinear dynamic systems without explaining the nature (physics) of the process. After all, vibration damping in a nonlinear dynamic system depends not only on the frictional force in the system or the magnitude of the vibration velocity force generated by the external excitation force, as studies show that the process is much more complex. In [9,13], the vibrations of two degrees of freedom of nonlinear dynamic systems are investigated, the frequencies of resonant and parametric vibrations are determined and it is shown that it is difficult to obtain a proper result by roughly selecting system parameters without understanding the processes in the system. The results also demonstrate that the system or subsystems generates a very wide spectrum of parametric excitation frequencies. However, only methods for resonant and parametric vibration frequencies of nonlinear dynamical systems have been developed, and the problem of its mathematical modeling has been solved. Therefore, in the design stage of a dynamic system, it is very important to create a mathematical model that, by considering the resonant, parametric and external excitation frequencies of the system, would allow reducing its vibration level and ensure safe working conditions. Thus, the aim of the work is to analyze the vibration damping process in a nonlinear dynamic system of one degree of freedom, to determine which system parameters and factors have a significant effect on vibration damping, and to show how to choose properly system parameters to minimize vibration level in the designed system.
2. A Study of Vibration Generation Features of a Nonlinear Dynamic System of One Degree of Freedom
An external excitation force acting in a non-linear dynamic system of one degree of freedom generates a very wide spectrum of vibrations at different frequencies [9]. The regularities of vibration generation in linear dynamic systems do not allow to explaining the ongoing phenomenon in a nonlinear dynamic system by generating and damping vibrations. Let us study a second-order nonlinear dynamical system of one degree of freedom, the parameters of which are: M = 5.0 kg; k = 100000 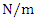 ;
; 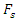 = 100000 N;
= 100000 N; 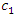 = 0.05; n = 2 and the natural frequencies (see (9)) are:
= 0.05; n = 2 and the natural frequencies (see (9)) are: 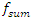 = 12.99 Hz;
= 12.99 Hz; 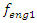 = 18.39 Hz;
= 18.39 Hz; 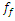 = 22.52 Hz;
= 22.52 Hz; 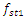 = 31.85 Hz [9]. To clarify the latter process, let us examine the vector scheme in Figure 1. We will notice that the vector
= 31.85 Hz [9]. To clarify the latter process, let us examine the vector scheme in Figure 1. We will notice that the vector 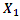 is sufficient to interpret linear dynamic system vibrations. Examining the projections of the vector
is sufficient to interpret linear dynamic system vibrations. Examining the projections of the vector 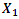 (Figure 1) on the coordinate axes 0x, 0y, we will notice that there are two features that characterize vibrations in a linear dynamic system:1. Condition of vibration symmetry on the coordinate axis 0x and 0y for all values of angle
(Figure 1) on the coordinate axes 0x, 0y, we will notice that there are two features that characterize vibrations in a linear dynamic system:1. Condition of vibration symmetry on the coordinate axis 0x and 0y for all values of angle 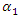 when it is within the range
when it is within the range 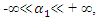 it means:
it means: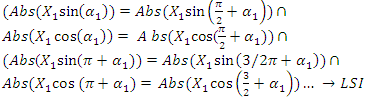 | (1) |
where LSI is linear system indicator;  is conjunction;
is conjunction;  is implication.2. The condition of the perpendicularity (orthogonally) of the velocity vector for the displacement vector.
is implication.2. The condition of the perpendicularity (orthogonally) of the velocity vector for the displacement vector. 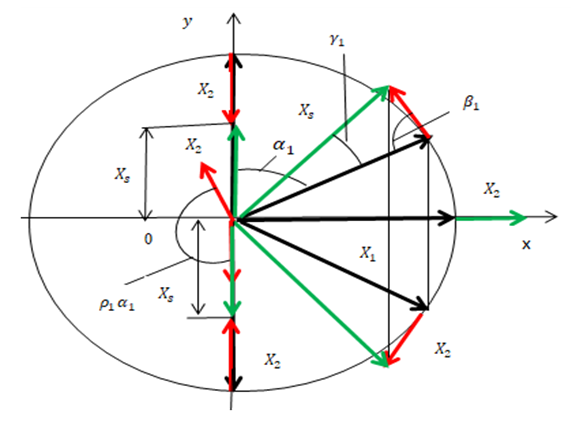 | Figure 1. Vector interpretation of vibrations of nonlinear dynamical systems of one degree of freedom, when 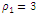 |
The accentuated conditions of vibration size symmetry of the coordinate axes 0x or 0y (1) and their orthogonally are very important features of a linear dynamic system and we will use them to study the physics of one-degree-of-freedom nonlinear dynamic system vibrations. Further research will not always emphasize that a nonlinear dynamic system with one degree of freedom is considered, as this is clear even from the title. Therefore, in a nonlinear dynamic system, a single vector 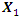 is not sufficient to graphically interpret vibrations. To understand the physics of vibrations generated in a nonlinear dynamical system in the first step, let us examine the vibrations generated by the sum of two vectors
is not sufficient to graphically interpret vibrations. To understand the physics of vibrations generated in a nonlinear dynamical system in the first step, let us examine the vibrations generated by the sum of two vectors 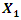 and
and 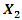 (Figure 1). We will assume that the vector
(Figure 1). We will assume that the vector 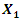 is the magnitude of the vibration amplitude generated by the excitation force
is the magnitude of the vibration amplitude generated by the excitation force 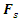 , and
, and 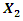 is the vibration amplitude of the second harmonic of the parametric excitation. In addition, the vector
is the vibration amplitude of the second harmonic of the parametric excitation. In addition, the vector 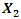 is lagging behind the vector
is lagging behind the vector 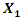 in
in 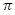 radians. While examining the magnitudes of the projections of the total vector
radians. While examining the magnitudes of the projections of the total vector 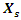 on the axes 0x and 0y, we will notice that the change in their size is determined by the regularities of the change in the angle
on the axes 0x and 0y, we will notice that the change in their size is determined by the regularities of the change in the angle 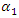 and
and 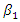 , where
, where 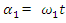 . The magnitude of the variation of the magnitude modules vector
. The magnitude of the variation of the magnitude modules vector 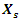 (Figure 1) is expressed as follows:
(Figure 1) is expressed as follows: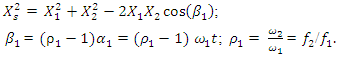 | (2) |
where 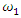 is the angular velocity of rotation of the vector
is the angular velocity of rotation of the vector 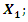
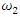 is the angular velocity of rotation of the vector
is the angular velocity of rotation of the vector 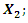 t is time;
t is time; 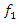 and
and 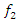 are the rotational frequencies of the vectors
are the rotational frequencies of the vectors 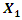 and
and 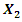 .From the dependencies of (2) it can be seen that the law of change of the total size
.From the dependencies of (2) it can be seen that the law of change of the total size 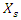 of the vector modules is related to the regularity of the change of
of the vector modules is related to the regularity of the change of 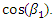 We will assume that in the present case the proportionality factor
We will assume that in the present case the proportionality factor 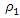 is
is 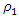 = 3. Four characteristic points can be distinguished by the analysis of dependencies (2):
= 3. Four characteristic points can be distinguished by the analysis of dependencies (2):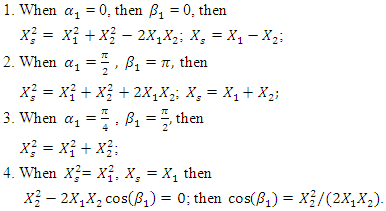 | (3) |
When 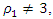 then there are also analog characteristic points, only they will be arranged differently. Analyzing the analytical expression of the fourth condition above (3), we will see that its requirement will be met when the inequality is satisfied:
then there are also analog characteristic points, only they will be arranged differently. Analyzing the analytical expression of the fourth condition above (3), we will see that its requirement will be met when the inequality is satisfied: 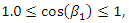 then
then 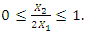 The fourth expression shows that the latter condition will be satisfied only when the dimensions of the vectors modules
The fourth expression shows that the latter condition will be satisfied only when the dimensions of the vectors modules 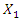 and
and 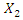 are matched to each other, in other words
are matched to each other, in other words 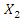 must be less than or equal to
must be less than or equal to 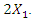 Consider the characteristic points of the phase-space diagram represented by the vector
Consider the characteristic points of the phase-space diagram represented by the vector 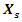 in the 0x, 0y coordinate system (Figure 2b). However, these characteristic points can be seen more clearly in Figure 1a. The first characteristic point in the diagram provided in Figure 1a will be when
in the 0x, 0y coordinate system (Figure 2b). However, these characteristic points can be seen more clearly in Figure 1a. The first characteristic point in the diagram provided in Figure 1a will be when 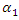 = 0 and
= 0 and 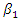 = 0, because then the conditions symmetry (1) of the linear vibration of the system also satisfied. Analogously examining conditions 2, 3 and 4 of the dependencies (3), we will observe that they satisfy the conditions of vibration symmetry and vector orthogonally. Thus, it was found that in a nonlinear dynamic system there are four characteristic points that satisfy the conditions of vibration symmetry with respect to the coordinate axes 0x and 0y. The projections of the vectors
= 0, because then the conditions symmetry (1) of the linear vibration of the system also satisfied. Analogously examining conditions 2, 3 and 4 of the dependencies (3), we will observe that they satisfy the conditions of vibration symmetry and vector orthogonally. Thus, it was found that in a nonlinear dynamic system there are four characteristic points that satisfy the conditions of vibration symmetry with respect to the coordinate axes 0x and 0y. The projections of the vectors 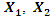 and
and 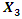 into the coordinate axes 0x and 0y are determined as follows:
into the coordinate axes 0x and 0y are determined as follows: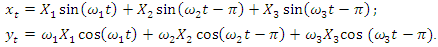 | (4) |
A phase-space diagram was obtained by calculating the vibrations of the second-order nonlinear dynamics system and their velocities upon applying the Runge-Kutta method (MATLAB) when it was excited at 10 Hz Figure 2a and the spectral density of the vibrations Figure 2c. From the spectral density Figure 2c, it can be seen that the maximum vibration amplitudes are achieved when the system vibrates at an excitation frequency of 10 Hz and the third parametric vibration frequency at a frequency of 30.12 Hz. The vibration level of the second harmonic of the parametric vibration 20 Hz is significantly lower than the frequencies mentioned above.. The increase in the vibration of the third harmonic of the parametric excitation can be explained by the fact that the frequency was very close to the resonant frequency of the system 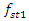 = 31.85 Hz. Therefore, for the frequencies of maximum vibration intensity
= 31.85 Hz. Therefore, for the frequencies of maximum vibration intensity 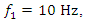
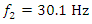 and
and 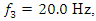 the system vibrations and velocities are calculated according to (4) and their phase-space diagram is shown in Fig. 2b. Calculations of nonlinear dynamic system vibrations and their velocities were also performed for other frequency ratio
the system vibrations and velocities are calculated according to (4) and their phase-space diagram is shown in Fig. 2b. Calculations of nonlinear dynamic system vibrations and their velocities were also performed for other frequency ratio 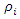 and their phase-face diagrams were drawn, for example, when
and their phase-face diagrams were drawn, for example, when 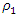 = 1.67 and
= 1.67 and 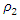 = 0.333 (Figure 3b). Comparing the phase-space diagrams of Figures -2a, 2b, 3a, and 3b, we observe that they are almost identical, although not all spectral density amplitudes have been estimated. When calculating the phase-space diagrams, it is observed that between the amplitudes
= 0.333 (Figure 3b). Comparing the phase-space diagrams of Figures -2a, 2b, 3a, and 3b, we observe that they are almost identical, although not all spectral density amplitudes have been estimated. When calculating the phase-space diagrams, it is observed that between the amplitudes 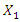 and
and 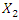 there is approximate ratio:
there is approximate ratio: 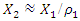 . In the event that
. In the event that 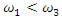 then
then 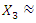
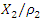 and when
and when 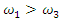 then
then 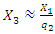 . The value of
. The value of 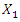 is approximated by solving the dependencies in (7), (9) or (11). It should be noted that the phase-space diagrams were obtained only when the values of the frequencies
is approximated by solving the dependencies in (7), (9) or (11). It should be noted that the phase-space diagrams were obtained only when the values of the frequencies 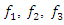 and the vibration amplitude vectors
and the vibration amplitude vectors 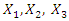 were exactly as shown in the figures below. The results of the phase-space diagram study show that we are going in the right direction and the study of vibration damping in a nonlinear dynamic system can be further investigated by the method under consideration.
were exactly as shown in the figures below. The results of the phase-space diagram study show that we are going in the right direction and the study of vibration damping in a nonlinear dynamic system can be further investigated by the method under consideration.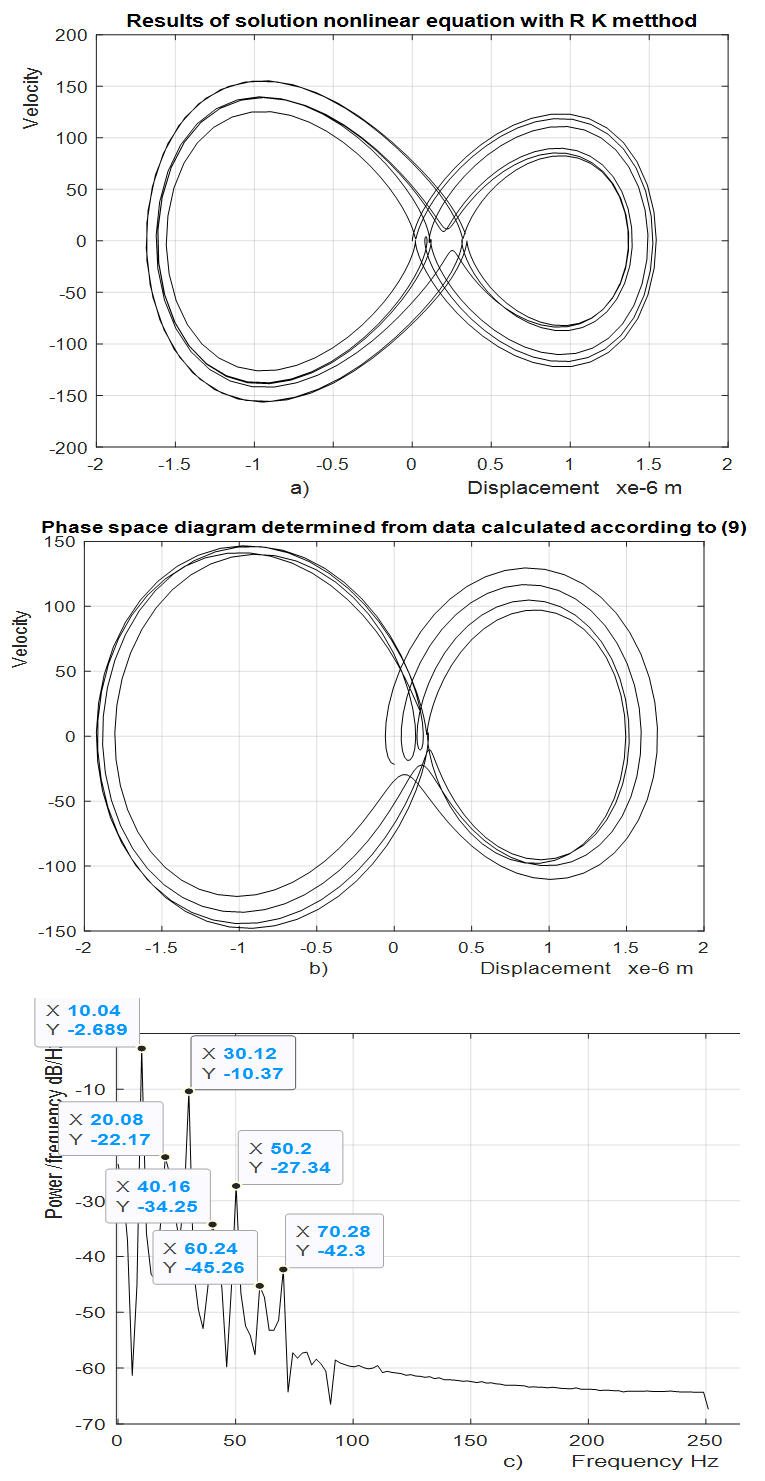 | Figure 2. Calculation results when 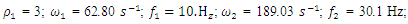 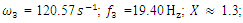 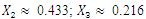 |
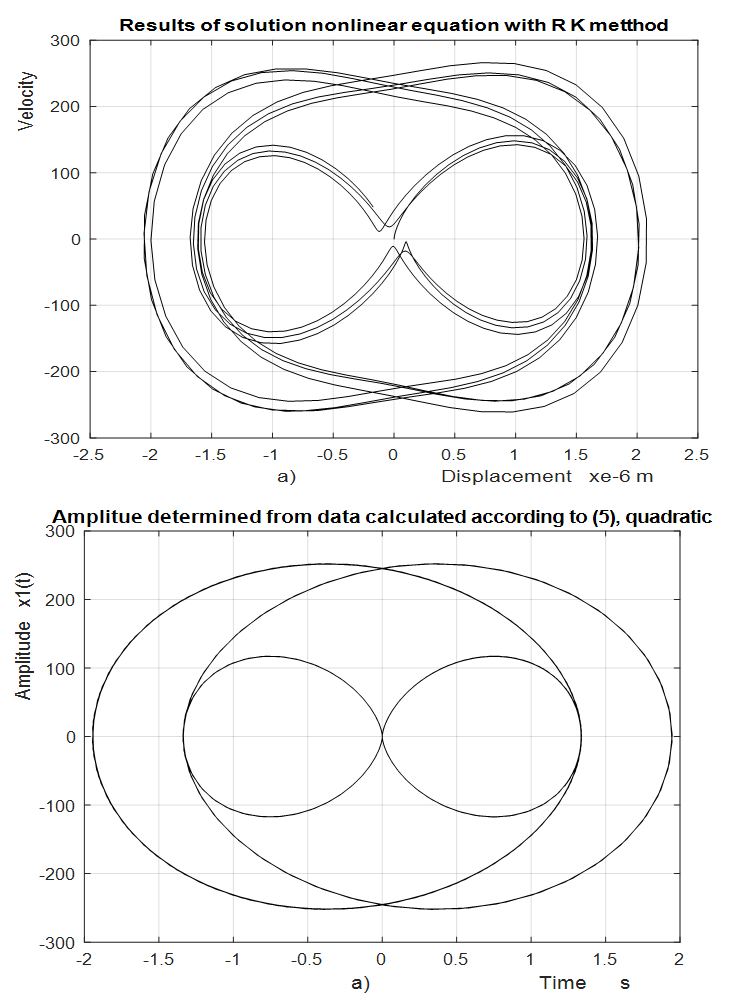 | Figure 3. Calculation results when 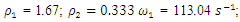 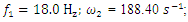 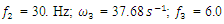 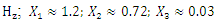 |
In the first step, we will consider the vector plan in Figure 4a, 4b and 4c which evaluates only the forces generated by the displacement of 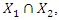 their velocity and acceleration in a nonlinear dynamic system. The projections of the latter forces into the coordinate axes 0x and 0y, at different
their velocity and acceleration in a nonlinear dynamic system. The projections of the latter forces into the coordinate axes 0x and 0y, at different 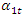 values, are shown in Figure 4b and c. According to the vector plan Figure - 4a and b it is possible to write the projections of the vectors to the coordinates 0x and 0y with the following dependencies:
values, are shown in Figure 4b and c. According to the vector plan Figure - 4a and b it is possible to write the projections of the vectors to the coordinates 0x and 0y with the following dependencies: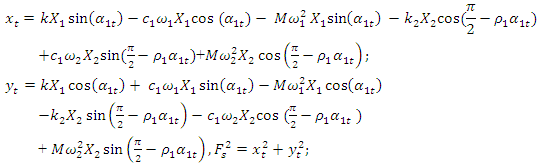 | (5) |
where k and 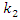 are the stiffness;
are the stiffness; 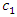 is damping coefficient;
is damping coefficient; 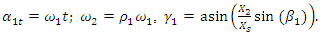 Let us examine how the expressions
Let us examine how the expressions 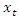 and
and 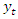 change at the characteristic points (3) of the dynamic system, when
change at the characteristic points (3) of the dynamic system, when 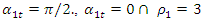 . Then equations (5) to the last
. Then equations (5) to the last 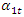 value will be rearranged as follows:
value will be rearranged as follows: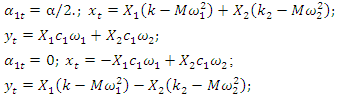 | (6) |
Then 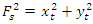 .A graphical illustration of the latter projections on the coordinate axes 0x, 0y is shown in Figure 4b and c.Analogously to any characteristic point (3), it is possible to obtain projections by force vectors on the coordinate axes 0x, 0y, when
.A graphical illustration of the latter projections on the coordinate axes 0x, 0y is shown in Figure 4b and c.Analogously to any characteristic point (3), it is possible to obtain projections by force vectors on the coordinate axes 0x, 0y, when 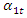 changes within
changes within 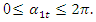 Assuming that in the force connections between the magnitude of vector
Assuming that in the force connections between the magnitude of vector 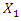 and
and 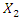 there exists an approximate equality
there exists an approximate equality 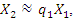 we will transform the dependencies (6) as follows:
we will transform the dependencies (6) as follows: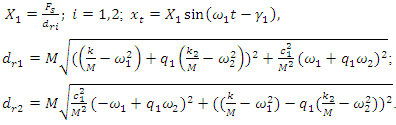 | (7) |
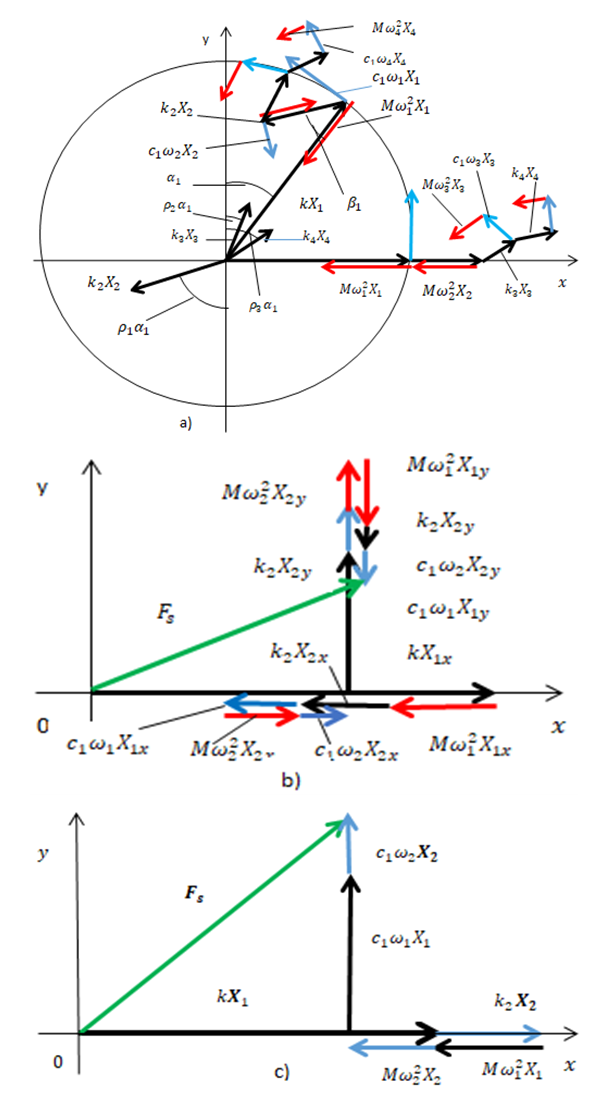 | Figure 4. Vector plans of acting force in a nonlinear dynamic system at different characteristic points where 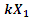 is displacement force vector of is displacement force vector of 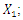 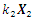 is displacement force vector of is displacement force vector of 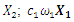 is velocity force vector of is velocity force vector of 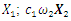 is velocity force vector of is velocity force vector of 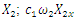 is the projection of the vector is the projection of the vector 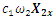 on the coordinate axis on the coordinate axis 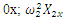 is the projection of the vector is the projection of the vector 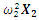 on the coordinate axis on the coordinate axis 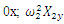 is the projection of the vector is the projection of the vector 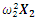 on the coordinate axis on the coordinate axis 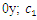 is coefficients of damping is coefficients of damping |
In the case of resonance, when 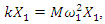 we will transform equations (7) as follows:
we will transform equations (7) as follows: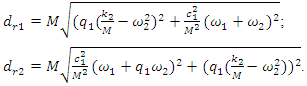 | (8) |
It can be seen from dependences (7) and (8) that even in the case of resonance, the vibrations are damped by forces generated at different frequencies by displacements, velocities, and accelerations. For further investigation, we will state that the vectors  are dynamic system vibration amplitudes and the value of
are dynamic system vibration amplitudes and the value of  is expressed as
is expressed as  In the case of the three-force vector plan
In the case of the three-force vector plan 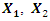 and
and 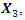 their projections on the coordinate axes 0x, 0y would be as follows:
their projections on the coordinate axes 0x, 0y would be as follows: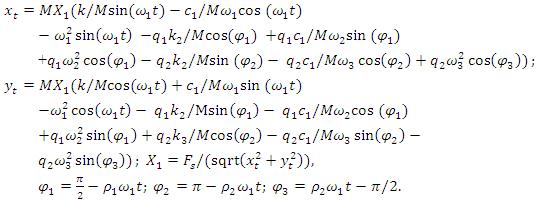 | (9) |
The equations (9) are long and we will not provide the analysis of the dependences of their 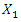 size on the dependencies of the dynamic system parameters in the equations. However, the final result of the previous analysis, when
size on the dependencies of the dynamic system parameters in the equations. However, the final result of the previous analysis, when 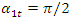 and
and 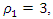 will be expressed as the following dependence:
will be expressed as the following dependence: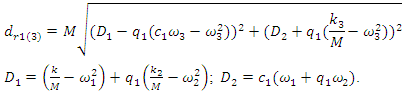 | (10) |
The expression of the dependence of the 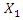 amplitudes on the four forces shown in Figure 4a would be much more complex, so that case is not considered at this stage. When we want to estimate more vibration amplitude vectors from spectral density and friction force vectors, then the phase-space diagram calculations must be performed in MATLAB as follows:
amplitudes on the four forces shown in Figure 4a would be much more complex, so that case is not considered at this stage. When we want to estimate more vibration amplitude vectors from spectral density and friction force vectors, then the phase-space diagram calculations must be performed in MATLAB as follows: 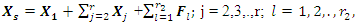 | (11) |
where 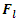 is friction force vectors.Then, analogously as calculated above, the values of the angles
is friction force vectors.Then, analogously as calculated above, the values of the angles 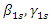 and the projections of the vector
and the projections of the vector 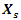 into the coordinate axes 0x and 0y are calculated. If we enter in notation (11) that
into the coordinate axes 0x and 0y are calculated. If we enter in notation (11) that 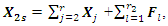 then we will have the sum of two vectors
then we will have the sum of two vectors 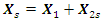 (see Figure 1), and then the dependencies obtained above and the conclusions will apply to the latter case. The vector diagram of the acting forces in the dynamic system, in the latter case, is drawn analogously to the above. Due to the complexity of the latter projections, they are not presented in this article. From the results of the analysis of dependencies (3), (5), (7), (9), (11) and others, and the results presented in Figures 1, 2 and 3, the following conclusions can be drawn:1. The calculation results performed according to (7) show that
(see Figure 1), and then the dependencies obtained above and the conclusions will apply to the latter case. The vector diagram of the acting forces in the dynamic system, in the latter case, is drawn analogously to the above. Due to the complexity of the latter projections, they are not presented in this article. From the results of the analysis of dependencies (3), (5), (7), (9), (11) and others, and the results presented in Figures 1, 2 and 3, the following conclusions can be drawn:1. The calculation results performed according to (7) show that 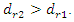 This means that the amplitude value
This means that the amplitude value 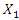 at the point when
at the point when 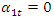 will be less than the amplitude value that the system will generate at the point when
will be less than the amplitude value that the system will generate at the point when 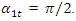 2. When
2. When 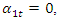 then the forces generated by the vibration velocity are the forces resisting the displacement of the system, and the forces generated by the stiffness and vibration acceleration become the vibration damping forces. This shows that the effect of the forces generated in a nonlinear dynamic system varies during one excitation force cycle.3. In a nonlinear dynamic system, vibrations are damped not only by the forces generated by the vibration velocity, but also by the forces generated by the harmonic displacement, vibration velocity, and acceleration of the other vibrations.4. Vibration amplitude
then the forces generated by the vibration velocity are the forces resisting the displacement of the system, and the forces generated by the stiffness and vibration acceleration become the vibration damping forces. This shows that the effect of the forces generated in a nonlinear dynamic system varies during one excitation force cycle.3. In a nonlinear dynamic system, vibrations are damped not only by the forces generated by the vibration velocity, but also by the forces generated by the harmonic displacement, vibration velocity, and acceleration of the other vibrations.4. Vibration amplitude 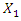 when
when 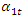 varies in the range
varies in the range 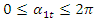 is of variable size.It must be emphasized that the amplitude magnitude
is of variable size.It must be emphasized that the amplitude magnitude 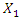 is a variable when
is a variable when 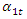 varies between
varies between 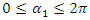 and
and 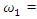 const. Meanwhile, in a linear dynamic system, when
const. Meanwhile, in a linear dynamic system, when 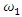 = constant then the magnitude of the vibrating amplitudes
= constant then the magnitude of the vibrating amplitudes 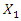 is also a constant value.
is also a constant value.
3. Vibration Damping Study, Numerical Analysis and Discussion
Whereas, the previously obtained expressions of force vectors projections on the coordinate axes 0x, 0y (5); (9) and (11) are complex, so further investigation of the relationship between excitation force magnitude and vibration intensity will be performed with the help of MATLAB. In the first stage, let us examine how the magnitude and damping of vibrations change in a nonlinear dynamic system when it is affected by the forces generated by the vectors 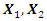 and
and 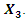 We will say that
We will say that 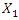 is the amplitude of the vibrations caused by the external excitation force, then it is also the amplitude of the vibrations of the first harmonic of the parametric excitation. The magnitude of the amplitudes
is the amplitude of the vibrations caused by the external excitation force, then it is also the amplitude of the vibrations of the first harmonic of the parametric excitation. The magnitude of the amplitudes 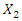 in the vibration spectrum density of Figure 2c is second in value and its vibration frequency is three times higher than
in the vibration spectrum density of Figure 2c is second in value and its vibration frequency is three times higher than 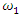 and the value of
and the value of 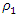 is
is 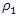 = 3. However,
= 3. However, 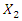 are the sum of the amplitudes of the third harmonic of the parametric excitation and the system resonant frequency
are the sum of the amplitudes of the third harmonic of the parametric excitation and the system resonant frequency 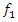 = 31.85 Hz.
= 31.85 Hz. 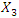 is only the amplitude of the second frequency parametric vibration, the frequency of which is twice as high as the frequency of the vibration amplitude
is only the amplitude of the second frequency parametric vibration, the frequency of which is twice as high as the frequency of the vibration amplitude 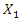 and the magnitude of the latter amplitude is less than
and the magnitude of the latter amplitude is less than 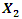 (Figure 2c). For further studies, it is necessary to at least approximately determine the values or dependences of the parameters
(Figure 2c). For further studies, it is necessary to at least approximately determine the values or dependences of the parameters 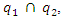 which are used in the above equations. To determine the ratio of the magnitudes between the different harmonic amplitudes at the resonant and parametric vibration frequencies, the energy and force relationship were used:
which are used in the above equations. To determine the ratio of the magnitudes between the different harmonic amplitudes at the resonant and parametric vibration frequencies, the energy and force relationship were used: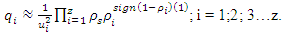 | (12) |
The energy relationship is determined by comparing the energy expressions: 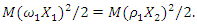 For the force connection (relation), the value of the parameter
For the force connection (relation), the value of the parameter 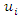 in work [9] is determined as follows:
in work [9] is determined as follows: 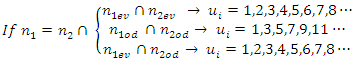 | (13) |
where 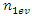 and
and 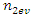 are even numbers;
are even numbers; 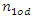 and
and 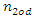 – odd numbers;
– odd numbers; 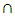 is conjunction;
is conjunction; 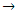 is implication;
is implication; 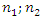 are exponents of
are exponents of 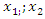 and show the degree of nonlinearity of dynamic systems; n is an indicator of nonlinearity.When
and show the degree of nonlinearity of dynamic systems; n is an indicator of nonlinearity.When 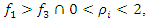 then the frequency of the latter harmonic
then the frequency of the latter harmonic 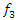 will be considered the subharmonic of the resonant frequency, which is closest to the excitation force frequency and then when
will be considered the subharmonic of the resonant frequency, which is closest to the excitation force frequency and then when 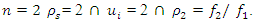 When
When 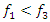 then
then 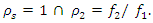 To elucidate in more detail how the magnitude of the vibration amplitude
To elucidate in more detail how the magnitude of the vibration amplitude 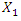 changes in the nonlinear dynamic system, varying
changes in the nonlinear dynamic system, varying 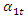 in the range
in the range 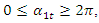 the calculations are performed using MATLAB according to formulas (5), (9) and (11). In order to verify the accuracy of the research results obtained by the method under consideration, the values of vibrations
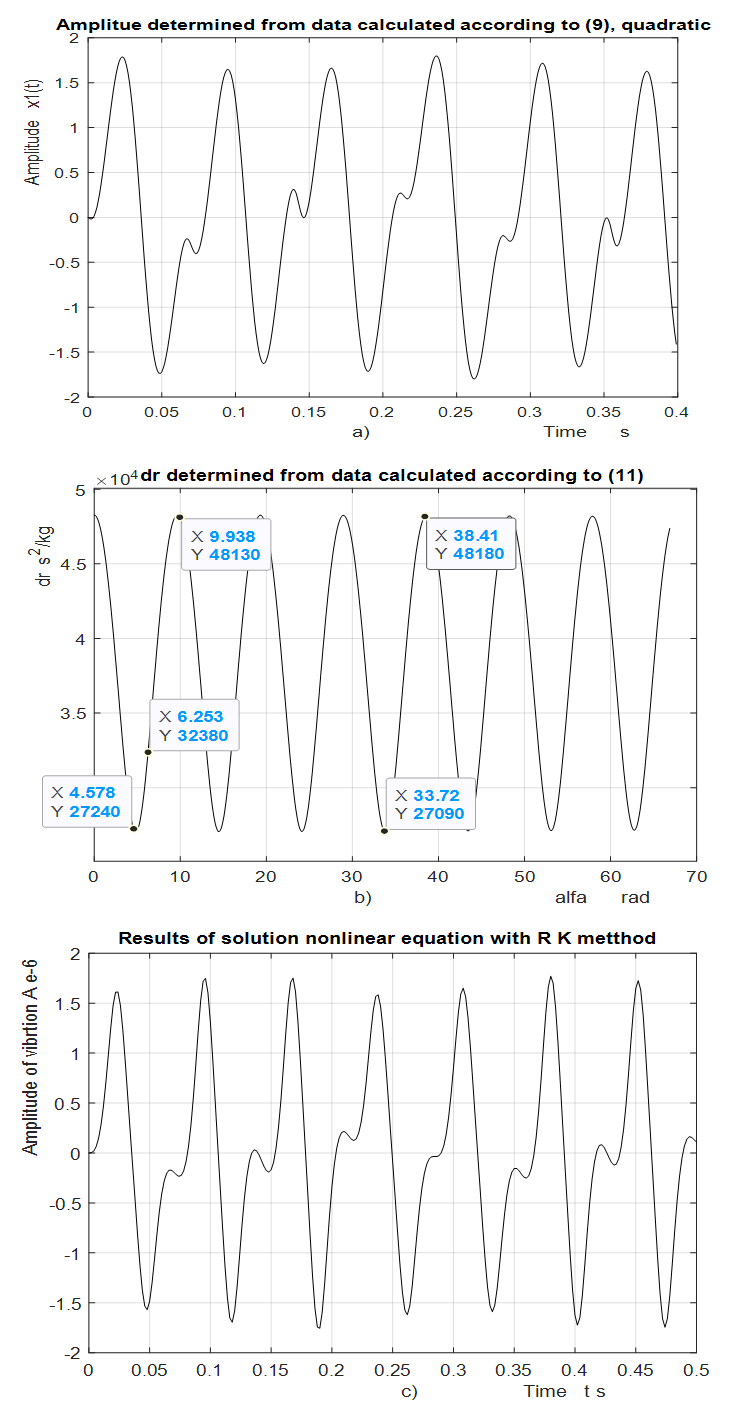
the calculations are performed using MATLAB according to formulas (5), (9) and (11). In order to verify the accuracy of the research results obtained by the method under consideration, the values of vibrations 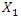 are calculated for the values of the same parameters by solving the nonlinear dynamic equations of quadratic and cubic nonlinearity. The calculation results of the latter are shown in Figure 5; 6 and 7. Analyzing the results presented in Figures 5, 6, 7 and Table 1 and comparing them with the results in Figures 2 and 3, the following summaries can be made:1. The extreme values corresponding to the four characteristic points of the nonlinear dynamical system (3) can be determined in a known way, which means that the expression of the first derivative of
are calculated for the values of the same parameters by solving the nonlinear dynamic equations of quadratic and cubic nonlinearity. The calculation results of the latter are shown in Figure 5; 6 and 7. Analyzing the results presented in Figures 5, 6, 7 and Table 1 and comparing them with the results in Figures 2 and 3, the following summaries can be made:1. The extreme values corresponding to the four characteristic points of the nonlinear dynamical system (3) can be determined in a known way, which means that the expression of the first derivative of 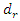 is set to zero. However, they can also be seen from the graph mentioned above. 2. The computational results obtained according to expresions (5) (9) and (11) matches quite well the results obtained by solving the dynamic systems of quadratic and cubic nonlinearity by the Runge-Kutto method, although not all spectral density vibration amplitudes have been estimated in the latter equations (calculations).3. The magnitude of the vibration amplitude
is set to zero. However, they can also be seen from the graph mentioned above. 2. The computational results obtained according to expresions (5) (9) and (11) matches quite well the results obtained by solving the dynamic systems of quadratic and cubic nonlinearity by the Runge-Kutto method, although not all spectral density vibration amplitudes have been estimated in the latter equations (calculations).3. The magnitude of the vibration amplitude 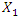 varies substantially during one external excitation cycle at a constant excitation frequency, because the value of the denominator dr (dynamic steefness) (7) or (10) changes in the latter range Figure 5 and 6. 4. If the frequency of the external excitation force coincides with some resonant frequency of the nonlinear dynamic system, then the forces generated by other vibration displacements, velocities and accelerations do not allow to significantly increase the amplitude of the vibrations at the resonant frequency.5. As the degree of nonlinearity of a nonlinear dynamical system increases, it becomes more stable, for example, when a quadratic nonlinearity system vibrates at a resonant frequency of
varies substantially during one external excitation cycle at a constant excitation frequency, because the value of the denominator dr (dynamic steefness) (7) or (10) changes in the latter range Figure 5 and 6. 4. If the frequency of the external excitation force coincides with some resonant frequency of the nonlinear dynamic system, then the forces generated by other vibration displacements, velocities and accelerations do not allow to significantly increase the amplitude of the vibrations at the resonant frequency.5. As the degree of nonlinearity of a nonlinear dynamical system increases, it becomes more stable, for example, when a quadratic nonlinearity system vibrates at a resonant frequency of 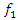 = 31.85 Hz, that is, the highest resonant frequency,
= 31.85 Hz, that is, the highest resonant frequency, 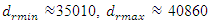 and
and 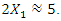 Meanwhile, for a system of cubic nonlinearity, vibrating at the highest resonant frequency f = 39.0 Hz,
Meanwhile, for a system of cubic nonlinearity, vibrating at the highest resonant frequency f = 39.0 Hz, 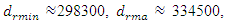 and
and 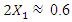 (Figure 7).6. The system itself determines the ratio of the magnitudes of the different amplitudes and the frequencies of the latter amplitude vibrations.7. The minimum and maximum
(Figure 7).6. The system itself determines the ratio of the magnitudes of the different amplitudes and the frequencies of the latter amplitude vibrations.7. The minimum and maximum 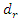 (dynamic steefness) values (Figure 5b, 6b), of the system, correspond to the characteristic points of the nonlinear dynamic system (3).
(dynamic steefness) values (Figure 5b, 6b), of the system, correspond to the characteristic points of the nonlinear dynamic system (3).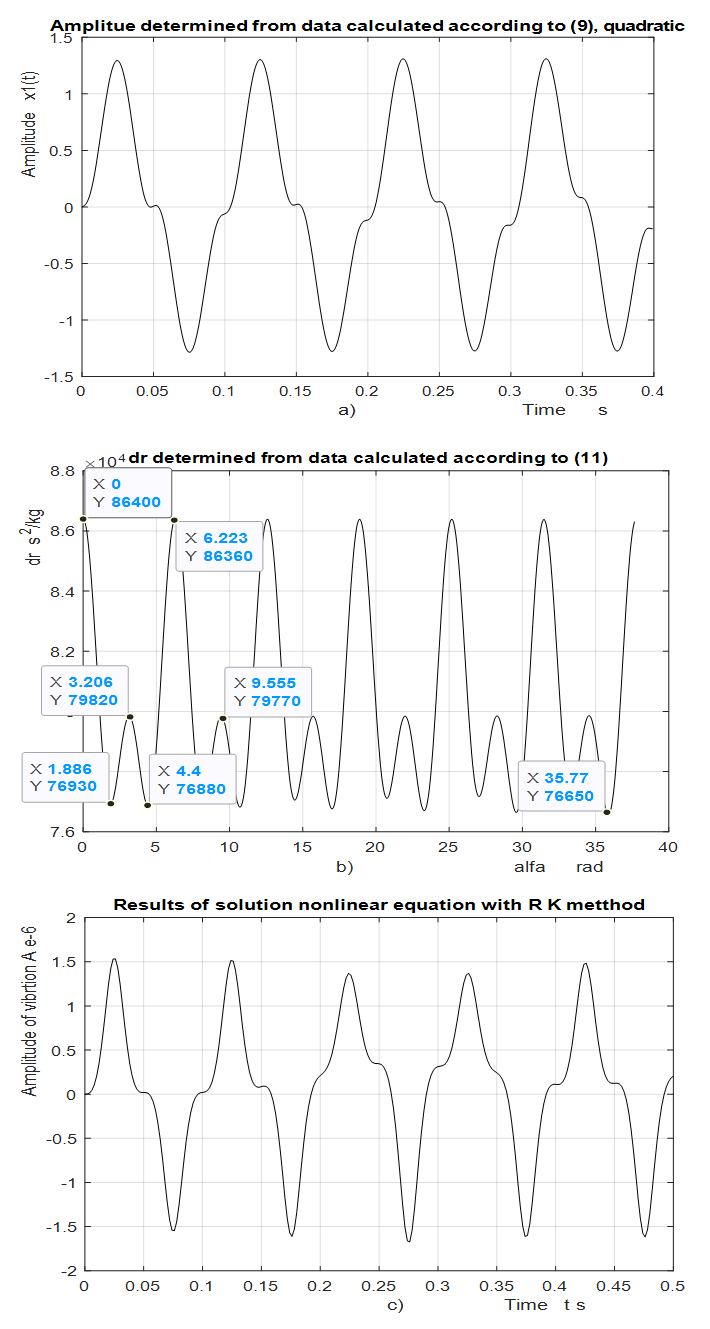 | Figure 5. Results of solution of vibration damping properties of nonlinear dynamic systems for quadratic nonlinearity, when 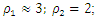 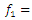 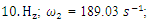 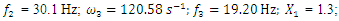 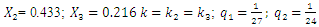 |
 | Figure 6. Results of solution of vibration damping properties of nonlinear dynamic systems for quadratic nonlinearity, when 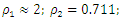 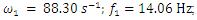    |
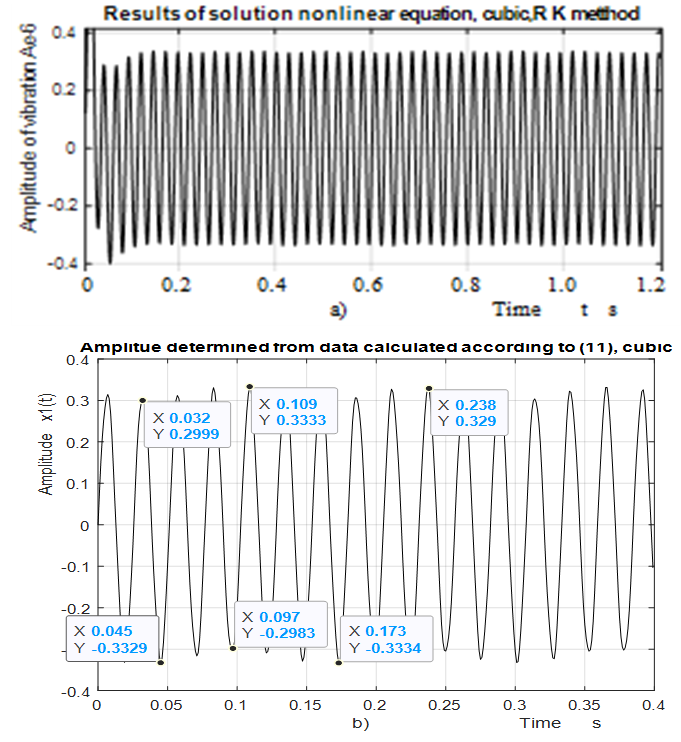 | Figure 7. Results of the dynamic system vibration damping reseach for cubic nonlinearity when 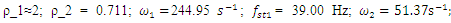 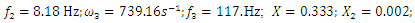 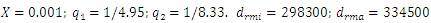 |
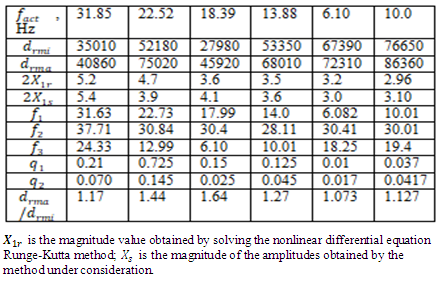
When the dynamic system was excited at resonant frequencies of 31.85 Hz, 22.52 Hz, 18.20 Hz, and 13.01 Hz, the 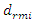 value ranged from 27980 <
value ranged from 27980 < 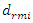 <53350 and the lowest
<53350 and the lowest 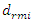 = 27980
= 27980 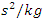 was at f = 18.20 Hz.Meanwhile, at the same parameters in a linear dynamic system, when the system vibrates at the highest resonant frequency, the value of
was at f = 18.20 Hz.Meanwhile, at the same parameters in a linear dynamic system, when the system vibrates at the highest resonant frequency, the value of 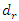 would be
would be 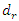 =5*
=5* 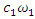 = 0.05*200.00 = 50,0
= 0.05*200.00 = 50,0 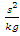 . Comparing the value
. Comparing the value 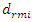 with the value
with the value 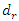 of the linear system, we notice that in the case under consideration, in a nonlinear dynamic system, even in the case of resonance, the vibrations are damped approximately 27980/50.
of the linear system, we notice that in the case under consideration, in a nonlinear dynamic system, even in the case of resonance, the vibrations are damped approximately 27980/50. 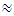 560 times more than in a linear system. The data in Table 1 show that as the excitation frequency increased from 10 Hz to 31.85 Hz, i., 31.85/10
560 times more than in a linear system. The data in Table 1 show that as the excitation frequency increased from 10 Hz to 31.85 Hz, i., 31.85/10 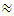 3.185 times, the amplitude of the vibrations increased from 2.96 to 5.2, i.e., 5.2/ 2.96
3.185 times, the amplitude of the vibrations increased from 2.96 to 5.2, i.e., 5.2/ 2.96 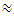 1.76 times, without changing the magnitude of the excitation force and the size of the dynamic system parameters In this way, the vibration level can be reduced by almost 2 times by properly choosing the values of the dynamic system parameters and the frequency of the external excitation force. Therefore, when choosing the external excitation force frequency
1.76 times, without changing the magnitude of the excitation force and the size of the dynamic system parameters In this way, the vibration level can be reduced by almost 2 times by properly choosing the values of the dynamic system parameters and the frequency of the external excitation force. Therefore, when choosing the external excitation force frequency 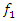 , care must be taken to ensure that it does not coincide or be repeated for the system's resonant frequencies and the system's lowest frequency subharmonicfrequency. If the frequencies of the forces mentioned above coincide with the frequency of the external excitation force then it is necessary to change the values of the system parameters (maybe it is enough to change the mass or the stiffness of the springs) and in this way the damping in the system will be increased. It is important to determine what the three main frequencies of the system are in the spectral density when we vibrate it at frequency
, care must be taken to ensure that it does not coincide or be repeated for the system's resonant frequencies and the system's lowest frequency subharmonicfrequency. If the frequencies of the forces mentioned above coincide with the frequency of the external excitation force then it is necessary to change the values of the system parameters (maybe it is enough to change the mass or the stiffness of the springs) and in this way the damping in the system will be increased. It is important to determine what the three main frequencies of the system are in the spectral density when we vibrate it at frequency 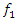 . The first and main frequency will be the external excitation force frequency
. The first and main frequency will be the external excitation force frequency 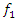 . The methodology for determining the exact frequencies
. The methodology for determining the exact frequencies 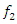 and
and 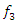 is not yet known. Of course, it is possible to solve nonlinear differential equations with the help of MATLAB and the obtained result will show vibrations of the largest amplitudes. However, some features have been observed in the studies, which allow to determine the values of the latter frequencies or to avoid an incorrect combination of them. First – do not choose the excitation force frequency for the coincident or close lowest frequency subharmonic frequency, as it will be a repeative of the maximum resonant frequency of the system and very close to a repeatitive of the other resonant frequencies, for example, when excited by a dynamic system at a frequency of 31.85 Hz, it still vibrates at frequencies
is not yet known. Of course, it is possible to solve nonlinear differential equations with the help of MATLAB and the obtained result will show vibrations of the largest amplitudes. However, some features have been observed in the studies, which allow to determine the values of the latter frequencies or to avoid an incorrect combination of them. First – do not choose the excitation force frequency for the coincident or close lowest frequency subharmonic frequency, as it will be a repeative of the maximum resonant frequency of the system and very close to a repeatitive of the other resonant frequencies, for example, when excited by a dynamic system at a frequency of 31.85 Hz, it still vibrates at frequencies 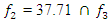 = 24.33 Hz Table 1, and for the latter three frequencies the frequency 6.1 Hz is repeatitive. Examining the data in Table 1, more examples can be observed when the 6.1 Hz frequency is a repeatytive of the vibration frequencies of a vibrating dynamic system.
= 24.33 Hz Table 1, and for the latter three frequencies the frequency 6.1 Hz is repeatitive. Examining the data in Table 1, more examples can be observed when the 6.1 Hz frequency is a repeatytive of the vibration frequencies of a vibrating dynamic system.Table 1. Summary of vibration damping reasioch results
 |
| |
|
Second, when the frequency of the external excitation force does not coincide with the resonant frequencies of the system and 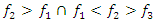 then
then 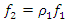 and
and 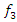 will be equal to the subharmonic frequency of the nearest resonant frequency
will be equal to the subharmonic frequency of the nearest resonant frequency 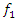 . In the case where
. In the case where 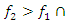
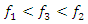 then
then 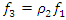 . Third, to increase the vibration damping in a nonlinear dynamic system, do not allow the parametric vibration frequencies to coincide with the resonant frequencies of the system. The performed research allowed: first – to explain the physics of vibration damping in a nonlinear dynamic system of one degree of freedom and showed the dependence of the damping magnitude on the combination of resonant, parametric vibrations and excitation force frequencies and second – to not subjectively choose the designed system values and excitation force frequency, that allow to increase the vibration damping in the system.. Thus, the results of the research show that the developed method accurately evaluates the process of vibration damping of a nonlinear dynamic system and the regularities and conclusions can be used to develop new systems with increased damping and reduced vibration levels. In addition, the latest research results allow the designer to choose the appropriate system parameters and determine safe operating conditions.
. Third, to increase the vibration damping in a nonlinear dynamic system, do not allow the parametric vibration frequencies to coincide with the resonant frequencies of the system. The performed research allowed: first – to explain the physics of vibration damping in a nonlinear dynamic system of one degree of freedom and showed the dependence of the damping magnitude on the combination of resonant, parametric vibrations and excitation force frequencies and second – to not subjectively choose the designed system values and excitation force frequency, that allow to increase the vibration damping in the system.. Thus, the results of the research show that the developed method accurately evaluates the process of vibration damping of a nonlinear dynamic system and the regularities and conclusions can be used to develop new systems with increased damping and reduced vibration levels. In addition, the latest research results allow the designer to choose the appropriate system parameters and determine safe operating conditions.
4. Conclusions
This work analyzes the process and method of vibration damping in a nonlinear dynamic system with one degree of freedom, estimating the excitation force, resonant and parametric vibration frequencies. Analytical methods have been developed that allow for quadratic and cubic nonlinearity dynamic systems to choose parameter values during the design process that would increase the damping of the system and reduce the vibration level of the developed system and ensure its safe operation.Analytical results The analytical results indicate that:1. In a nonlinear dynamic system, the vibrations are damped not only by the force generated by the velocity of the vibrations excited by the external excitation force, but also by the forces generated by the displacements, velocities, and accelerations of vibrations at other frequencies. 2. The forces generated in a nonlinear dynamical system may at some times be like vibration-exciting forces, and at other times - vibration-damping forces. 3. The dynamic stiffness of a nonlinear dynamic system varies over one external excitation force cycle without changing the value of the excitation frequency and parameters.4. The magnitude of the vibration damping in a nonlinear dynamic system depends on the proper matching of the resonant, parametric vibrations and external force frequencies.The results of numerical calculationsThe results of numerical calculations allow us to prove that:1. The dynamic stiffness 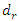 of a nonlinear system have extreme points at which it acquires the highest or lowest values during one excitation frequency cycle.2. As the excitation frequency of a nonlinear dynamic system varies, the spectral density and phase-space diagram of its vibrations change.3. The system itself determines the vibration frequencies and the ratio of their amplitudes.4. It has been determend that in the case of resonances of a nonlinear dynamic system, the vibrations are damped several hundred times more than in a linear dynamic system.5. The vibration level can be reduced by almost 2 times by properly choosing the values of the dynamic system parameters and the frequency of the external excitation force.6. The developed method evaluates the nonlinear dynamic system vibration damping process with sufficient accuracy and can be used in the development of new systems.
of a nonlinear system have extreme points at which it acquires the highest or lowest values during one excitation frequency cycle.2. As the excitation frequency of a nonlinear dynamic system varies, the spectral density and phase-space diagram of its vibrations change.3. The system itself determines the vibration frequencies and the ratio of their amplitudes.4. It has been determend that in the case of resonances of a nonlinear dynamic system, the vibrations are damped several hundred times more than in a linear dynamic system.5. The vibration level can be reduced by almost 2 times by properly choosing the values of the dynamic system parameters and the frequency of the external excitation force.6. The developed method evaluates the nonlinear dynamic system vibration damping process with sufficient accuracy and can be used in the development of new systems.
References
| [1] | Chopra AK, 2011. Dynamics of Structures. 4th edn. Prentice Hall, Upper Saddle River, NJ. |
| [2] | Zhu S., J., Zheng Y., F., Fu Yiming, 2004. Analysis of non-linear dynamics of a two-degree-of-freedom vibration system with non-linear damping and non-linear spring. Journal of Sound and Vibration, 271 (1-2); pp.15-24. DOI: 10.1016/S0022-460X(03)00249-9. |
| [3] | Qingdong Chai, Jin Zeng, HuiMa, Kunli, Qinkai Han, 2020. A dynamic modeling approach for nonlinear vibration analysis of the L-type pipeline system with clamps. Chinese Journal of Aeronautics, Volume 33, Issue 12, pp. 3253-3265. |
| [4] | M.Y. Liu, Z.C. Wang, Z.D. Zhou, et al. 2018. Vibration response of multi-span fluid-conveying pipe with multiple accessories under complex boundary conditions Eur. J Mech. A-Solid, 72), pp. 41-56. |
| [5] | Y.F. Zhang, M.H. Yao, W. Zhang, et al. 2017. Dynamical modeling and multi-pulse chaotic dynamics of cantilevered. Aerosp Sci Technol, 68, pp. 441-453. |
| [6] | Z. Luo, J.W. Wang, R. Tang, et al. 2019. Research on vibration performance of the nonlinear combined support-flexible rotor system Nonlinear Dynam, 98 (1), pp. 113-128. |
| [7] | S. L. Han1 and Takeshi Kinoshita1, 2012. Nonlinear damping identification in nonlinear dynamic system based on stochastic inverse approach. Matthematical problems in engineering, Volume 10, pp.65-72. |
| [8] | S. J. Elliot, M. Gedrachi Tehrani and R. S. Langley, 2014. Nonlinear damping and qasi-linear modrling. Mathematical, phisical and engineering sciences. 2015. https://doi.Org/10.1098/rsta.2014.0402. |
| [9] | Mariūnas M., 2020, Methods for determining resonant and parametric excitation frequencies of nonlinear two degree of freedom dynamic systems. American Journal of Computational and Applied Mathematics, 10(2), pp. 39-47. |
| [10] | Willians R. A. Gody, Markelo A. Trinda de, 2020. Disign and analysis of a geometrically nonlnear dynamic vibration absorber. ASME Journal of computational and nonlinear dynamics. Volume 15(8), p. 9. |
| [11] | Marco Amabili, 2018. Derivation of nonlinear damping from viscoelasticity in case of nonlinear vibrations. Nonlinear dynamics. Volume 97, pp. 1785-1797. |
| [12] | Yuanping Li, Xuemin Wang, Siyu Chen, Hongbing Lu, 2018. Nonlinear dynamic response and global stability of an air compressor vibration system. Journal of Low Frequency Noise, Vibration and Active Contro, Volue 38(3-4), pp. 1081-1095. DOI: 10.1177/1461348418817695. |
| [13] | Mariūnas M., 2021, Methods for a research model of nonlinear two degree of freedom dynamic systems. American Journal of Computational and Applied Mathematics, 11(1), pp. 1-11. |



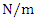 ;
; 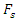 = 100000 N;
= 100000 N; 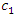 = 0.05; n = 2 and the natural frequencies (see (9)) are:
= 0.05; n = 2 and the natural frequencies (see (9)) are: 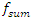 = 12.99 Hz;
= 12.99 Hz; 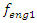 = 18.39 Hz;
= 18.39 Hz; 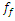 = 22.52 Hz;
= 22.52 Hz; 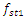 = 31.85 Hz [9]. To clarify the latter process, let us examine the vector scheme in Figure 1. We will notice that the vector
= 31.85 Hz [9]. To clarify the latter process, let us examine the vector scheme in Figure 1. We will notice that the vector 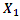 is sufficient to interpret linear dynamic system vibrations. Examining the projections of the vector
is sufficient to interpret linear dynamic system vibrations. Examining the projections of the vector 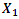 (Figure 1) on the coordinate axes 0x, 0y, we will notice that there are two features that characterize vibrations in a linear dynamic system:1. Condition of vibration symmetry on the coordinate axis 0x and 0y for all values of angle
(Figure 1) on the coordinate axes 0x, 0y, we will notice that there are two features that characterize vibrations in a linear dynamic system:1. Condition of vibration symmetry on the coordinate axis 0x and 0y for all values of angle 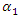 when it is within the range
when it is within the range 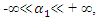 it means:
it means: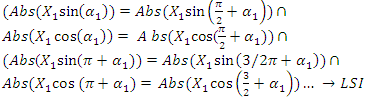
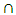 is conjunction;
is conjunction;  is implication.2. The condition of the perpendicularity (orthogonally) of the velocity vector for the displacement vector.
is implication.2. The condition of the perpendicularity (orthogonally) of the velocity vector for the displacement vector. 
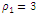
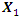 is not sufficient to graphically interpret vibrations. To understand the physics of vibrations generated in a nonlinear dynamical system in the first step, let us examine the vibrations generated by the sum of two vectors
is not sufficient to graphically interpret vibrations. To understand the physics of vibrations generated in a nonlinear dynamical system in the first step, let us examine the vibrations generated by the sum of two vectors 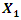 and
and 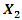 (Figure 1). We will assume that the vector
(Figure 1). We will assume that the vector 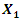 is the magnitude of the vibration amplitude generated by the excitation force
is the magnitude of the vibration amplitude generated by the excitation force 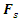 , and
, and 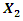 is the vibration amplitude of the second harmonic of the parametric excitation. In addition, the vector
is the vibration amplitude of the second harmonic of the parametric excitation. In addition, the vector 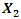 is lagging behind the vector
is lagging behind the vector 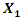 in
in 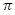 radians. While examining the magnitudes of the projections of the total vector
radians. While examining the magnitudes of the projections of the total vector 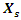 on the axes 0x and 0y, we will notice that the change in their size is determined by the regularities of the change in the angle
on the axes 0x and 0y, we will notice that the change in their size is determined by the regularities of the change in the angle 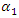 and
and 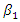 , where
, where 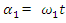 . The magnitude of the variation of the magnitude modules vector
. The magnitude of the variation of the magnitude modules vector 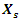 (Figure 1) is expressed as follows:
(Figure 1) is expressed as follows: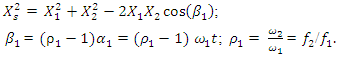
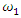 is the angular velocity of rotation of the vector
is the angular velocity of rotation of the vector 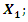
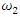 is the angular velocity of rotation of the vector
is the angular velocity of rotation of the vector 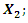 t is time;
t is time; 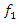 and
and 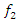 are the rotational frequencies of the vectors
are the rotational frequencies of the vectors 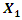 and
and 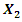 .From the dependencies of (2) it can be seen that the law of change of the total size
.From the dependencies of (2) it can be seen that the law of change of the total size 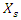 of the vector modules is related to the regularity of the change of
of the vector modules is related to the regularity of the change of 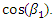 We will assume that in the present case the proportionality factor
We will assume that in the present case the proportionality factor 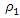 is
is 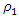 = 3. Four characteristic points can be distinguished by the analysis of dependencies (2):
= 3. Four characteristic points can be distinguished by the analysis of dependencies (2):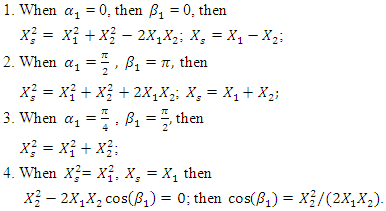
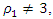 then there are also analog characteristic points, only they will be arranged differently. Analyzing the analytical expression of the fourth condition above (3), we will see that its requirement will be met when the inequality is satisfied:
then there are also analog characteristic points, only they will be arranged differently. Analyzing the analytical expression of the fourth condition above (3), we will see that its requirement will be met when the inequality is satisfied: 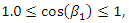 then
then 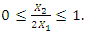 The fourth expression shows that the latter condition will be satisfied only when the dimensions of the vectors modules
The fourth expression shows that the latter condition will be satisfied only when the dimensions of the vectors modules 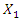 and
and 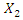 are matched to each other, in other words
are matched to each other, in other words 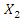 must be less than or equal to
must be less than or equal to 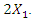 Consider the characteristic points of the phase-space diagram represented by the vector
Consider the characteristic points of the phase-space diagram represented by the vector 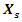 in the 0x, 0y coordinate system (Figure 2b). However, these characteristic points can be seen more clearly in Figure 1a. The first characteristic point in the diagram provided in Figure 1a will be when
in the 0x, 0y coordinate system (Figure 2b). However, these characteristic points can be seen more clearly in Figure 1a. The first characteristic point in the diagram provided in Figure 1a will be when 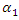 = 0 and
= 0 and 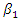 = 0, because then the conditions symmetry (1) of the linear vibration of the system also satisfied. Analogously examining conditions 2, 3 and 4 of the dependencies (3), we will observe that they satisfy the conditions of vibration symmetry and vector orthogonally. Thus, it was found that in a nonlinear dynamic system there are four characteristic points that satisfy the conditions of vibration symmetry with respect to the coordinate axes 0x and 0y. The projections of the vectors
= 0, because then the conditions symmetry (1) of the linear vibration of the system also satisfied. Analogously examining conditions 2, 3 and 4 of the dependencies (3), we will observe that they satisfy the conditions of vibration symmetry and vector orthogonally. Thus, it was found that in a nonlinear dynamic system there are four characteristic points that satisfy the conditions of vibration symmetry with respect to the coordinate axes 0x and 0y. The projections of the vectors 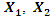 and
and 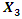 into the coordinate axes 0x and 0y are determined as follows:
into the coordinate axes 0x and 0y are determined as follows: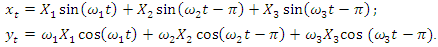
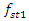 = 31.85 Hz. Therefore, for the frequencies of maximum vibration intensity
= 31.85 Hz. Therefore, for the frequencies of maximum vibration intensity 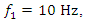
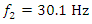 and
and 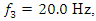 the system vibrations and velocities are calculated according to (4) and their phase-space diagram is shown in Fig. 2b. Calculations of nonlinear dynamic system vibrations and their velocities were also performed for other frequency ratio
the system vibrations and velocities are calculated according to (4) and their phase-space diagram is shown in Fig. 2b. Calculations of nonlinear dynamic system vibrations and their velocities were also performed for other frequency ratio 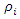 and their phase-face diagrams were drawn, for example, when
and their phase-face diagrams were drawn, for example, when 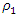 = 1.67 and
= 1.67 and 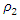 = 0.333 (Figure 3b). Comparing the phase-space diagrams of Figures -2a, 2b, 3a, and 3b, we observe that they are almost identical, although not all spectral density amplitudes have been estimated. When calculating the phase-space diagrams, it is observed that between the amplitudes
= 0.333 (Figure 3b). Comparing the phase-space diagrams of Figures -2a, 2b, 3a, and 3b, we observe that they are almost identical, although not all spectral density amplitudes have been estimated. When calculating the phase-space diagrams, it is observed that between the amplitudes 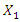 and
and 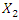 there is approximate ratio:
there is approximate ratio: 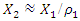 . In the event that
. In the event that 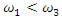 then
then 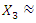
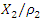 and when
and when 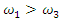 then
then 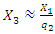 . The value of
. The value of 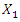 is approximated by solving the dependencies in (7), (9) or (11). It should be noted that the phase-space diagrams were obtained only when the values of the frequencies
is approximated by solving the dependencies in (7), (9) or (11). It should be noted that the phase-space diagrams were obtained only when the values of the frequencies 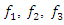 and the vibration amplitude vectors
and the vibration amplitude vectors 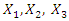 were exactly as shown in the figures below. The results of the phase-space diagram study show that we are going in the right direction and the study of vibration damping in a nonlinear dynamic system can be further investigated by the method under consideration.
were exactly as shown in the figures below. The results of the phase-space diagram study show that we are going in the right direction and the study of vibration damping in a nonlinear dynamic system can be further investigated by the method under consideration.
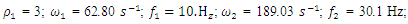
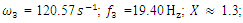
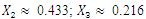

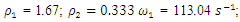
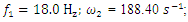
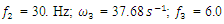
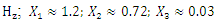
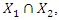 their velocity and acceleration in a nonlinear dynamic system. The projections of the latter forces into the coordinate axes 0x and 0y, at different
their velocity and acceleration in a nonlinear dynamic system. The projections of the latter forces into the coordinate axes 0x and 0y, at different 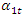 values, are shown in Figure 4b and c. According to the vector plan Figure - 4a and b it is possible to write the projections of the vectors to the coordinates 0x and 0y with the following dependencies:
values, are shown in Figure 4b and c. According to the vector plan Figure - 4a and b it is possible to write the projections of the vectors to the coordinates 0x and 0y with the following dependencies: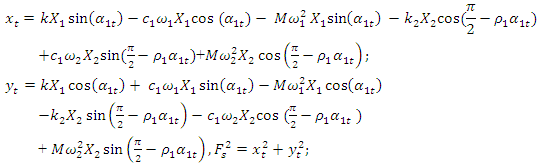
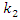 are the stiffness;
are the stiffness; 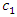 is damping coefficient;
is damping coefficient; 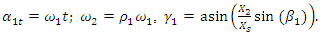 Let us examine how the expressions
Let us examine how the expressions 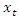 and
and 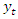 change at the characteristic points (3) of the dynamic system, when
change at the characteristic points (3) of the dynamic system, when 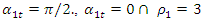 . Then equations (5) to the last
. Then equations (5) to the last 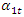 value will be rearranged as follows:
value will be rearranged as follows: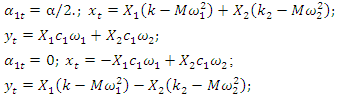
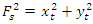 .A graphical illustration of the latter projections on the coordinate axes 0x, 0y is shown in Figure 4b and c.Analogously to any characteristic point (3), it is possible to obtain projections by force vectors on the coordinate axes 0x, 0y, when
.A graphical illustration of the latter projections on the coordinate axes 0x, 0y is shown in Figure 4b and c.Analogously to any characteristic point (3), it is possible to obtain projections by force vectors on the coordinate axes 0x, 0y, when 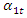 changes within
changes within 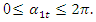 Assuming that in the force connections between the magnitude of vector
Assuming that in the force connections between the magnitude of vector 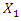 and
and 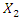 there exists an approximate equality
there exists an approximate equality 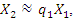 we will transform the dependencies (6) as follows:
we will transform the dependencies (6) as follows: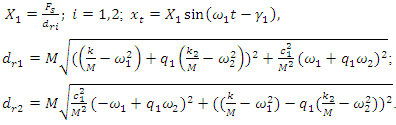
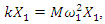 we will transform equations (7) as follows:
we will transform equations (7) as follows: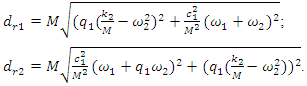
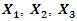 are dynamic system vibration amplitudes and the value of
are dynamic system vibration amplitudes and the value of 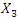 is expressed as
is expressed as 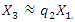 In the case of the three-force vector plan
In the case of the three-force vector plan 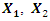 and
and 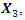 their projections on the coordinate axes 0x, 0y would be as follows:
their projections on the coordinate axes 0x, 0y would be as follows: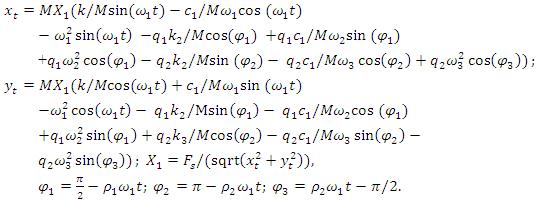
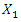 size on the dependencies of the dynamic system parameters in the equations. However, the final result of the previous analysis, when
size on the dependencies of the dynamic system parameters in the equations. However, the final result of the previous analysis, when 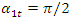 and
and 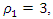 will be expressed as the following dependence:
will be expressed as the following dependence: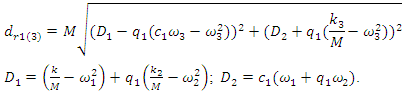
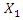 amplitudes on the four forces shown in Figure 4a would be much more complex, so that case is not considered at this stage. When we want to estimate more vibration amplitude vectors from spectral density and friction force vectors, then the phase-space diagram calculations must be performed in MATLAB as follows:
amplitudes on the four forces shown in Figure 4a would be much more complex, so that case is not considered at this stage. When we want to estimate more vibration amplitude vectors from spectral density and friction force vectors, then the phase-space diagram calculations must be performed in MATLAB as follows: 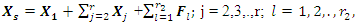
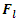 is friction force vectors.Then, analogously as calculated above, the values of the angles
is friction force vectors.Then, analogously as calculated above, the values of the angles 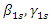 and the projections of the vector
and the projections of the vector 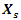 into the coordinate axes 0x and 0y are calculated. If we enter in notation (11) that
into the coordinate axes 0x and 0y are calculated. If we enter in notation (11) that 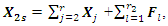 then we will have the sum of two vectors
then we will have the sum of two vectors 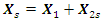 (see Figure 1), and then the dependencies obtained above and the conclusions will apply to the latter case. The vector diagram of the acting forces in the dynamic system, in the latter case, is drawn analogously to the above. Due to the complexity of the latter projections, they are not presented in this article. From the results of the analysis of dependencies (3), (5), (7), (9), (11) and others, and the results presented in Figures 1, 2 and 3, the following conclusions can be drawn:1. The calculation results performed according to (7) show that
(see Figure 1), and then the dependencies obtained above and the conclusions will apply to the latter case. The vector diagram of the acting forces in the dynamic system, in the latter case, is drawn analogously to the above. Due to the complexity of the latter projections, they are not presented in this article. From the results of the analysis of dependencies (3), (5), (7), (9), (11) and others, and the results presented in Figures 1, 2 and 3, the following conclusions can be drawn:1. The calculation results performed according to (7) show that 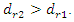 This means that the amplitude value
This means that the amplitude value 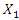 at the point when
at the point when 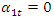 will be less than the amplitude value that the system will generate at the point when
will be less than the amplitude value that the system will generate at the point when 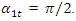 2. When
2. When 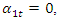 then the forces generated by the vibration velocity are the forces resisting the displacement of the system, and the forces generated by the stiffness and vibration acceleration become the vibration damping forces. This shows that the effect of the forces generated in a nonlinear dynamic system varies during one excitation force cycle.3. In a nonlinear dynamic system, vibrations are damped not only by the forces generated by the vibration velocity, but also by the forces generated by the harmonic displacement, vibration velocity, and acceleration of the other vibrations.4. Vibration amplitude
then the forces generated by the vibration velocity are the forces resisting the displacement of the system, and the forces generated by the stiffness and vibration acceleration become the vibration damping forces. This shows that the effect of the forces generated in a nonlinear dynamic system varies during one excitation force cycle.3. In a nonlinear dynamic system, vibrations are damped not only by the forces generated by the vibration velocity, but also by the forces generated by the harmonic displacement, vibration velocity, and acceleration of the other vibrations.4. Vibration amplitude 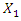 when
when 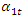 varies in the range
varies in the range 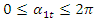 is of variable size.It must be emphasized that the amplitude magnitude
is of variable size.It must be emphasized that the amplitude magnitude 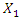 is a variable when
is a variable when 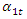 varies between
varies between 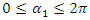 and
and 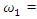 const. Meanwhile, in a linear dynamic system, when
const. Meanwhile, in a linear dynamic system, when 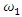 = constant then the magnitude of the vibrating amplitudes
= constant then the magnitude of the vibrating amplitudes 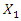 is also a constant value.
is also a constant value. 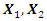 and
and 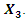 We will say that
We will say that 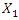 is the amplitude of the vibrations caused by the external excitation force, then it is also the amplitude of the vibrations of the first harmonic of the parametric excitation. The magnitude of the amplitudes
is the amplitude of the vibrations caused by the external excitation force, then it is also the amplitude of the vibrations of the first harmonic of the parametric excitation. The magnitude of the amplitudes 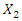 in the vibration spectrum density of Figure 2c is second in value and its vibration frequency is three times higher than
in the vibration spectrum density of Figure 2c is second in value and its vibration frequency is three times higher than 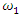 and the value of
and the value of 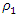 is
is 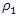 = 3. However,
= 3. However, 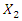 are the sum of the amplitudes of the third harmonic of the parametric excitation and the system resonant frequency
are the sum of the amplitudes of the third harmonic of the parametric excitation and the system resonant frequency 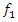 = 31.85 Hz.
= 31.85 Hz. 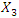 is only the amplitude of the second frequency parametric vibration, the frequency of which is twice as high as the frequency of the vibration amplitude
is only the amplitude of the second frequency parametric vibration, the frequency of which is twice as high as the frequency of the vibration amplitude 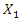 and the magnitude of the latter amplitude is less than
and the magnitude of the latter amplitude is less than 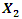 (Figure 2c). For further studies, it is necessary to at least approximately determine the values or dependences of the parameters
(Figure 2c). For further studies, it is necessary to at least approximately determine the values or dependences of the parameters 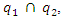 which are used in the above equations. To determine the ratio of the magnitudes between the different harmonic amplitudes at the resonant and parametric vibration frequencies, the energy and force relationship were used:
which are used in the above equations. To determine the ratio of the magnitudes between the different harmonic amplitudes at the resonant and parametric vibration frequencies, the energy and force relationship were used: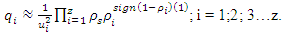
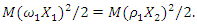 For the force connection (relation), the value of the parameter
For the force connection (relation), the value of the parameter 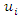 in work [9] is determined as follows:
in work [9] is determined as follows: 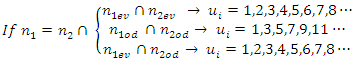
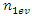 and
and 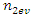 are even numbers;
are even numbers; 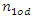 and
and 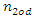 – odd numbers;
– odd numbers; 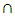 is conjunction;
is conjunction; 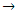 is implication;
is implication; 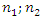 are exponents of
are exponents of 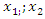 and show the degree of nonlinearity of dynamic systems; n is an indicator of nonlinearity.When
and show the degree of nonlinearity of dynamic systems; n is an indicator of nonlinearity.When 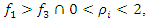 then the frequency of the latter harmonic
then the frequency of the latter harmonic 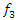 will be considered the subharmonic of the resonant frequency, which is closest to the excitation force frequency and then when
will be considered the subharmonic of the resonant frequency, which is closest to the excitation force frequency and then when 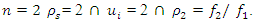 When
When 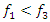 then
then 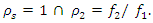 To elucidate in more detail how the magnitude of the vibration amplitude
To elucidate in more detail how the magnitude of the vibration amplitude 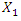 changes in the nonlinear dynamic system, varying
changes in the nonlinear dynamic system, varying 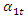 in the range
in the range 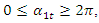 the calculations are performed using MATLAB according to formulas (5), (9) and (11). In order to verify the accuracy of the research results obtained by the method under consideration, the values of vibrations
the calculations are performed using MATLAB according to formulas (5), (9) and (11). In order to verify the accuracy of the research results obtained by the method under consideration, the values of vibrations 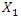 are calculated for the values of the same parameters by solving the nonlinear dynamic equations of quadratic and cubic nonlinearity. The calculation results of the latter are shown in Figure 5; 6 and 7. Analyzing the results presented in Figures 5, 6, 7 and Table 1 and comparing them with the results in Figures 2 and 3, the following summaries can be made:1. The extreme values corresponding to the four characteristic points of the nonlinear dynamical system (3) can be determined in a known way, which means that the expression of the first derivative of
are calculated for the values of the same parameters by solving the nonlinear dynamic equations of quadratic and cubic nonlinearity. The calculation results of the latter are shown in Figure 5; 6 and 7. Analyzing the results presented in Figures 5, 6, 7 and Table 1 and comparing them with the results in Figures 2 and 3, the following summaries can be made:1. The extreme values corresponding to the four characteristic points of the nonlinear dynamical system (3) can be determined in a known way, which means that the expression of the first derivative of 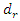 is set to zero. However, they can also be seen from the graph mentioned above. 2. The computational results obtained according to expresions (5) (9) and (11) matches quite well the results obtained by solving the dynamic systems of quadratic and cubic nonlinearity by the Runge-Kutto method, although not all spectral density vibration amplitudes have been estimated in the latter equations (calculations).3. The magnitude of the vibration amplitude
is set to zero. However, they can also be seen from the graph mentioned above. 2. The computational results obtained according to expresions (5) (9) and (11) matches quite well the results obtained by solving the dynamic systems of quadratic and cubic nonlinearity by the Runge-Kutto method, although not all spectral density vibration amplitudes have been estimated in the latter equations (calculations).3. The magnitude of the vibration amplitude 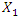 varies substantially during one external excitation cycle at a constant excitation frequency, because the value of the denominator dr (dynamic steefness) (7) or (10) changes in the latter range Figure 5 and 6. 4. If the frequency of the external excitation force coincides with some resonant frequency of the nonlinear dynamic system, then the forces generated by other vibration displacements, velocities and accelerations do not allow to significantly increase the amplitude of the vibrations at the resonant frequency.5. As the degree of nonlinearity of a nonlinear dynamical system increases, it becomes more stable, for example, when a quadratic nonlinearity system vibrates at a resonant frequency of
varies substantially during one external excitation cycle at a constant excitation frequency, because the value of the denominator dr (dynamic steefness) (7) or (10) changes in the latter range Figure 5 and 6. 4. If the frequency of the external excitation force coincides with some resonant frequency of the nonlinear dynamic system, then the forces generated by other vibration displacements, velocities and accelerations do not allow to significantly increase the amplitude of the vibrations at the resonant frequency.5. As the degree of nonlinearity of a nonlinear dynamical system increases, it becomes more stable, for example, when a quadratic nonlinearity system vibrates at a resonant frequency of 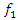 = 31.85 Hz, that is, the highest resonant frequency,
= 31.85 Hz, that is, the highest resonant frequency, 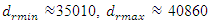 and
and 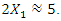 Meanwhile, for a system of cubic nonlinearity, vibrating at the highest resonant frequency f = 39.0 Hz,
Meanwhile, for a system of cubic nonlinearity, vibrating at the highest resonant frequency f = 39.0 Hz, 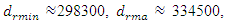 and
and 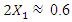 (Figure 7).6. The system itself determines the ratio of the magnitudes of the different amplitudes and the frequencies of the latter amplitude vibrations.7. The minimum and maximum
(Figure 7).6. The system itself determines the ratio of the magnitudes of the different amplitudes and the frequencies of the latter amplitude vibrations.7. The minimum and maximum 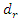 (dynamic steefness) values (Figure 5b, 6b), of the system, correspond to the characteristic points of the nonlinear dynamic system (3).
(dynamic steefness) values (Figure 5b, 6b), of the system, correspond to the characteristic points of the nonlinear dynamic system (3).
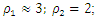
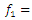
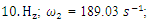
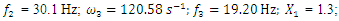
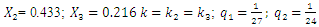

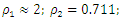
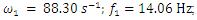
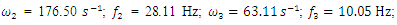
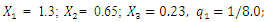
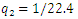

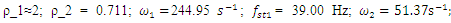
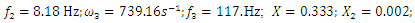
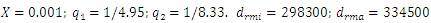
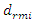 value ranged from 27980 <
value ranged from 27980 < 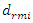 <53350 and the lowest
<53350 and the lowest 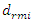 = 27980
= 27980 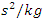 was at f = 18.20 Hz.Meanwhile, at the same parameters in a linear dynamic system, when the system vibrates at the highest resonant frequency, the value of
was at f = 18.20 Hz.Meanwhile, at the same parameters in a linear dynamic system, when the system vibrates at the highest resonant frequency, the value of 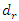 would be
would be 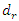 =5*
=5* 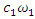 = 0.05*200.00 = 50,0
= 0.05*200.00 = 50,0 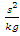 . Comparing the value
. Comparing the value 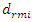 with the value
with the value 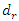 of the linear system, we notice that in the case under consideration, in a nonlinear dynamic system, even in the case of resonance, the vibrations are damped approximately 27980/50.
of the linear system, we notice that in the case under consideration, in a nonlinear dynamic system, even in the case of resonance, the vibrations are damped approximately 27980/50. 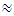 560 times more than in a linear system. The data in Table 1 show that as the excitation frequency increased from 10 Hz to 31.85 Hz, i., 31.85/10
560 times more than in a linear system. The data in Table 1 show that as the excitation frequency increased from 10 Hz to 31.85 Hz, i., 31.85/10 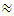 3.185 times, the amplitude of the vibrations increased from 2.96 to 5.2, i.e., 5.2/ 2.96
3.185 times, the amplitude of the vibrations increased from 2.96 to 5.2, i.e., 5.2/ 2.96 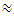 1.76 times, without changing the magnitude of the excitation force and the size of the dynamic system parameters In this way, the vibration level can be reduced by almost 2 times by properly choosing the values of the dynamic system parameters and the frequency of the external excitation force. Therefore, when choosing the external excitation force frequency
1.76 times, without changing the magnitude of the excitation force and the size of the dynamic system parameters In this way, the vibration level can be reduced by almost 2 times by properly choosing the values of the dynamic system parameters and the frequency of the external excitation force. Therefore, when choosing the external excitation force frequency  , care must be taken to ensure that it does not coincide or be repeated for the system's resonant frequencies and the system's lowest frequency subharmonicfrequency. If the frequencies of the forces mentioned above coincide with the frequency of the external excitation force then it is necessary to change the values of the system parameters (maybe it is enough to change the mass or the stiffness of the springs) and in this way the damping in the system will be increased. It is important to determine what the three main frequencies of the system are in the spectral density when we vibrate it at frequency
, care must be taken to ensure that it does not coincide or be repeated for the system's resonant frequencies and the system's lowest frequency subharmonicfrequency. If the frequencies of the forces mentioned above coincide with the frequency of the external excitation force then it is necessary to change the values of the system parameters (maybe it is enough to change the mass or the stiffness of the springs) and in this way the damping in the system will be increased. It is important to determine what the three main frequencies of the system are in the spectral density when we vibrate it at frequency  . The first and main frequency will be the external excitation force frequency
. The first and main frequency will be the external excitation force frequency 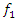 . The methodology for determining the exact frequencies
. The methodology for determining the exact frequencies 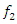 and
and 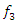 is not yet known. Of course, it is possible to solve nonlinear differential equations with the help of MATLAB and the obtained result will show vibrations of the largest amplitudes. However, some features have been observed in the studies, which allow to determine the values of the latter frequencies or to avoid an incorrect combination of them. First – do not choose the excitation force frequency for the coincident or close lowest frequency subharmonic frequency, as it will be a repeative of the maximum resonant frequency of the system and very close to a repeatitive of the other resonant frequencies, for example, when excited by a dynamic system at a frequency of 31.85 Hz, it still vibrates at frequencies
is not yet known. Of course, it is possible to solve nonlinear differential equations with the help of MATLAB and the obtained result will show vibrations of the largest amplitudes. However, some features have been observed in the studies, which allow to determine the values of the latter frequencies or to avoid an incorrect combination of them. First – do not choose the excitation force frequency for the coincident or close lowest frequency subharmonic frequency, as it will be a repeative of the maximum resonant frequency of the system and very close to a repeatitive of the other resonant frequencies, for example, when excited by a dynamic system at a frequency of 31.85 Hz, it still vibrates at frequencies 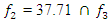 = 24.33 Hz Table 1, and for the latter three frequencies the frequency 6.1 Hz is repeatitive. Examining the data in Table 1, more examples can be observed when the 6.1 Hz frequency is a repeatytive of the vibration frequencies of a vibrating dynamic system.
= 24.33 Hz Table 1, and for the latter three frequencies the frequency 6.1 Hz is repeatitive. Examining the data in Table 1, more examples can be observed when the 6.1 Hz frequency is a repeatytive of the vibration frequencies of a vibrating dynamic system.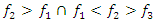 then
then 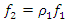 and
and 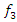 will be equal to the subharmonic frequency of the nearest resonant frequency
will be equal to the subharmonic frequency of the nearest resonant frequency 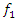 . In the case where
. In the case where 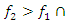
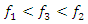 then
then 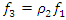 . Third, to increase the vibration damping in a nonlinear dynamic system, do not allow the parametric vibration frequencies to coincide with the resonant frequencies of the system. The performed research allowed: first – to explain the physics of vibration damping in a nonlinear dynamic system of one degree of freedom and showed the dependence of the damping magnitude on the combination of resonant, parametric vibrations and excitation force frequencies and second – to not subjectively choose the designed system values and excitation force frequency, that allow to increase the vibration damping in the system.. Thus, the results of the research show that the developed method accurately evaluates the process of vibration damping of a nonlinear dynamic system and the regularities and conclusions can be used to develop new systems with increased damping and reduced vibration levels. In addition, the latest research results allow the designer to choose the appropriate system parameters and determine safe operating conditions.
. Third, to increase the vibration damping in a nonlinear dynamic system, do not allow the parametric vibration frequencies to coincide with the resonant frequencies of the system. The performed research allowed: first – to explain the physics of vibration damping in a nonlinear dynamic system of one degree of freedom and showed the dependence of the damping magnitude on the combination of resonant, parametric vibrations and excitation force frequencies and second – to not subjectively choose the designed system values and excitation force frequency, that allow to increase the vibration damping in the system.. Thus, the results of the research show that the developed method accurately evaluates the process of vibration damping of a nonlinear dynamic system and the regularities and conclusions can be used to develop new systems with increased damping and reduced vibration levels. In addition, the latest research results allow the designer to choose the appropriate system parameters and determine safe operating conditions. 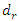 of a nonlinear system have extreme points at which it acquires the highest or lowest values during one excitation frequency cycle.2. As the excitation frequency of a nonlinear dynamic system varies, the spectral density and phase-space diagram of its vibrations change.3. The system itself determines the vibration frequencies and the ratio of their amplitudes.4. It has been determend that in the case of resonances of a nonlinear dynamic system, the vibrations are damped several hundred times more than in a linear dynamic system.5. The vibration level can be reduced by almost 2 times by properly choosing the values of the dynamic system parameters and the frequency of the external excitation force.6. The developed method evaluates the nonlinear dynamic system vibration damping process with sufficient accuracy and can be used in the development of new systems.
of a nonlinear system have extreme points at which it acquires the highest or lowest values during one excitation frequency cycle.2. As the excitation frequency of a nonlinear dynamic system varies, the spectral density and phase-space diagram of its vibrations change.3. The system itself determines the vibration frequencies and the ratio of their amplitudes.4. It has been determend that in the case of resonances of a nonlinear dynamic system, the vibrations are damped several hundred times more than in a linear dynamic system.5. The vibration level can be reduced by almost 2 times by properly choosing the values of the dynamic system parameters and the frequency of the external excitation force.6. The developed method evaluates the nonlinear dynamic system vibration damping process with sufficient accuracy and can be used in the development of new systems.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
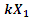 is displacement force vector of
is displacement force vector of 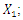
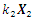 is displacement force vector of
is displacement force vector of 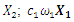 is velocity force vector of
is velocity force vector of 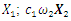 is velocity force vector of
is velocity force vector of 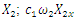 is the projection of the vector
is the projection of the vector 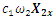 on the coordinate axis
on the coordinate axis 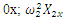 is the projection of the vector
is the projection of the vector 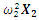 on the coordinate axis
on the coordinate axis 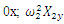 is the projection of the vector
is the projection of the vector 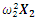 on the coordinate axis
on the coordinate axis 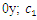 is coefficients of damping
is coefficients of damping