-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2021; 11(2): 21-29
doi:10.5923/j.ajcam.20211102.01
Received: Mar. 6, 2021; Accepted: Mar. 26, 2021; Published: Apr. 3, 2021

Auditing of Queueing Systems under Various Frame-Works
A. P. Panta1, R. P. Ghimire2, Dinesh Panthi3, Shankar Raj Pant4
1Department of Mathematics, Tri-Chandra Campus, Tribhuvan University, Kathmandu, Nepal
2Department of Mathematics, Kathmandu University, Kavre, Nepal
3Department of Mathematics, Valmeeki Campus, Nepal Sanskrit University, Kathmandu, Nepal
4Central Department of Mathematics, Tribhuvan University, Kirtipur, Nepal
Correspondence to: A. P. Panta, Department of Mathematics, Tri-Chandra Campus, Tribhuvan University, Kathmandu, Nepal.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This paper deals with the extensive survey of the queueing system from its birth in1909 to till date. As the time passes on old-provisions cannot tackle new-problem so newconcepts have to be developed. Some of the policies that have been developed from time to time have reported. Some of the prominent techniques of solution of queueing system have also been cited. As an illustration various queueing routing formulas are given in tabular form.
Keywords: Queue, Policy, Solution techniques
Cite this paper: A. P. Panta, R. P. Ghimire, Dinesh Panthi, Shankar Raj Pant, Auditing of Queueing Systems under Various Frame-Works, American Journal of Computational and Applied Mathematics , Vol. 11 No. 2, 2021, pp. 21-29. doi: 10.5923/j.ajcam.20211102.01.
Article Outline
1. Introduction
- Queueing is a waiting line and queues are encountered in many of our daily life from morning to late night such as to cash cheques or deposit money at the bank, the mathematics waiting to be executed in the computer, the cases in the court to be decided, the mobile calls waiting for free channel in the base station. Needless to say that queues can be of tangible objects or of intangible objects. Queue forms when service seeker cannot find the service immediately upon its arrival into the service facilities. The entities which need service are called customers and the entities which provide service in a specified rule are called servers such as vehicles are the customers and the petrol-station is the server. Queue is the science of waiting line. Since the introduction of queueing concept by a Danish tele-com engineer A.K. Erlang in 1909, this area of research has faced so many ups and down in its development. With the advent of modern technology of computer science, the research in queueing system has widened its wings in widespread area of applications such as agriculture to space science. The objective of study of queueing system is to make the balance between the cost of waiting and cost of service. The study of queueing system is aimed at the reduction of waiting time either by providing the additional servers or by providing additional waiting space. The ultimate goal of queueing system is to understand the mechanism of whole system and to improve the existing system. This study is aimed at presenting development trend of queueing system, their forms and applications in modern real life situations. Moreover up to date survey of literatures is the focus-point of our studies. From view point of the size of buffer of the queueing system there can be two types of queues (i) Infinite buffer capacity queueing system (ii) Finite buffer capacity queueing system.(i) Infinite buffer capacityIf we have provision of infinite buffer capacity which is possible when arrival rate is higher than service rate, then queue size will keep growing to an infinitely large size and system becomes unstable.(ii) Finite buffer capacityQueueing analysis of finite system is more realistic in applications than infinite system. It has been shown that bigger the finite capacity is, the better the approximation. In the one hand the exact overflow probabilities for infinite capacity queueing model is the ‘worst-case’ results for finite capacity system and in the other hand approximation of finite queueing system is made by the infinite capacity queueing system with some amount of safety margin.
2. Classification of Queueing System
- Depending upon the probability distribution of arrivals and service time distributions, the queueing systems can be classified as (i) Markovian queueing system (ii) Semi-Markovian queueing system and (iii) Non-Markovian queueing system.
2.1. Markovian Queueing System
- If the arrival rate follows a Poisson distribution and service rate follows an exponential distribution then the queueing system is known as the Markovian queueing system. Historically, these have also been the systems used in the early stages of queueing theory to help decision making in the telephone industry. The underlying Markov process representing the number of customers in such systems is referred as a birth-and-death process such as
2.2. Semi-Markovian Queueing System
- If either inter-arrival times or service times do not follow the exponential distribution then the queueing system is known as the semi-Markovian queueing system such as
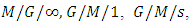
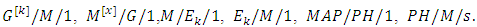
2.3. Non-Markovian Queueing System
- If both inter-arrival times and service times are non-exponentially distributed then the queueing system is known as the non-Markovian queueing system such as
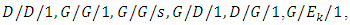
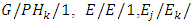
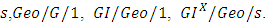
3. Development of Various Queueing Models
- Systematic study of queueing models can be made only after taking following policies into considerations- exhaustive, limited, gated, exhaustive limited (E-limited), gated limited (G-limited), N-policy, D-policy, T-policy, F-policy vacations which are provisioned to make the model more applicable.N-policy queueing system: The server starts service to arriving customers when the number reaches up to some fixed value N. The concept of N-policy was introduced by Yadin and Naor [1] in 1963. D-policy queueing system: The server starts service to waiting customer when cumulative service times achieved some threshold value D. The concept of D-policy was introduced by Balachandran [2] in 1973.T-policy: Every server requires exactly r customers to begin the service. If i is the number of customers and is less than r then the server waits for (r-i) more customers to be presented before start the service and server checks (scans) every T units of time. Heyman [3] first introduced the concept of T-policy in 1977.F-Policy: When number of customers in the system reaches its capacity
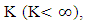 no further arriving customers are allowed to enter into the system until a certain number of customers, who are already in the system have been served in order to makethe number of customers in the system decreases to a predetermined threshold F
no further arriving customers are allowed to enter into the system until a certain number of customers, who are already in the system have been served in order to makethe number of customers in the system decreases to a predetermined threshold F 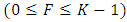 . Gupta [4] first introduced the concept of the F-policy in 1995.Some overview of some queueing models development is worthwhile to present in this section-
. Gupta [4] first introduced the concept of the F-policy in 1995.Some overview of some queueing models development is worthwhile to present in this section-3.1. Markovian Models
- Detailed discussion on Markovian queueing models are found in Gross et al. [5] and Castaneda et al. [6]. In Markovian models, the analysis is conducted applying the memoryless property of the exponential distribution.Severalresearchers have contributed to the study of finite capacity Markovian queueing models. It is worth noting to mention some of the contributions. Jain [7] studied finite capacity
 queueing system with queue-dependent heterogeneous servers and used recursive method to solve the steady state system of equations governing the model. Ke et al. [8] considered an F-policy
queueing system with queue-dependent heterogeneous servers and used recursive method to solve the steady state system of equations governing the model. Ke et al. [8] considered an F-policy 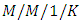 queueing system with a second optional service and obtained the steady-state analytic solutions. Shahin et al. [9] gave an alternative approach to determine the optimal number of servers by considering the level of customer satisfaction and the total cost in a queueing system. Cruz et al. [10] evaluated the behavior of a traffic intensity estimator for a single server finite Markovian queues. Fazlollahtabar and Gholizadeh [11] made economic analysis of the finite capacity
queueing system with a second optional service and obtained the steady-state analytic solutions. Shahin et al. [9] gave an alternative approach to determine the optimal number of servers by considering the level of customer satisfaction and the total cost in a queueing system. Cruz et al. [10] evaluated the behavior of a traffic intensity estimator for a single server finite Markovian queues. Fazlollahtabar and Gholizadeh [11] made economic analysis of the finite capacity 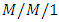 queueing system with different arrival rates and service rates. Very recently, Wu et al. [12] dealt with the optimization of Markov queueing model in hospital bed resource allocation and they analyzed the previous research models of related knowledge of queueing theory in medical services and summarized the advantages and disadvantages of the queueing model.Many researchers have contributed to the study of vacation and working vacation queueing models. Levy and Yechiali [13] first introduced the concept of vacation in 1975, where the idle time of the server is utilized for additional work in a secondary system. Servi and Finn [14] studied
queueing system with different arrival rates and service rates. Very recently, Wu et al. [12] dealt with the optimization of Markov queueing model in hospital bed resource allocation and they analyzed the previous research models of related knowledge of queueing theory in medical services and summarized the advantages and disadvantages of the queueing model.Many researchers have contributed to the study of vacation and working vacation queueing models. Levy and Yechiali [13] first introduced the concept of vacation in 1975, where the idle time of the server is utilized for additional work in a secondary system. Servi and Finn [14] studied 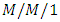 queues with working vacations, where the server works at a lower service rate rather than completely stopping service during the vacation period and generalized classical single server vacation model. Liu et al. [15] demonstrated stochastic decomposition structures of the queue length and waiting time in an
queues with working vacations, where the server works at a lower service rate rather than completely stopping service during the vacation period and generalized classical single server vacation model. Liu et al. [15] demonstrated stochastic decomposition structures of the queue length and waiting time in an 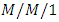 queue with working vacations and obtained the distributions of the additional queue length and additional delay. Jain and Jain [16] studied a single server working vacation queueing model with multiple types of server breakdowns and proposed a matrix geometric approach for computing the stationary queue length distribution. Ibe and Isijola [17] dealt with an
queue with working vacations and obtained the distributions of the additional queue length and additional delay. Jain and Jain [16] studied a single server working vacation queueing model with multiple types of server breakdowns and proposed a matrix geometric approach for computing the stationary queue length distribution. Ibe and Isijola [17] dealt with an 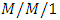 queueing system in which two types of vacations can be taken by the server and they obtained steady-state solution. Maurya [18] demonstrated a mathematical modeling for analyzing a Markovian queueing system with two heterogeneous servers and working vacation and obtained various performance measures of the Markovian queueing system with varying parameters under steady state using matrix geometric method. Tian et al. [19] analyzed the customer strategic behavior in the
queueing system in which two types of vacations can be taken by the server and they obtained steady-state solution. Maurya [18] demonstrated a mathematical modeling for analyzing a Markovian queueing system with two heterogeneous servers and working vacation and obtained various performance measures of the Markovian queueing system with varying parameters under steady state using matrix geometric method. Tian et al. [19] analyzed the customer strategic behavior in the 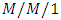 queueing system with working vacations and vacation interruptions where arriving customers have option to decide whether to join the system or balk. Kalyanaraman and Sundaramoorthy [20] studied a single server Markovian queue with multiple working vacation and partial breakdown using matrix geometric method.In real world, many queueing situations arise in which there may be a tendency of customers to be discouraged by a long queue. Consequently, the customers either decide not to join the queue (balking) or depart after joining the queue without getting the service due to impatience (reneging). An
queueing system with working vacations and vacation interruptions where arriving customers have option to decide whether to join the system or balk. Kalyanaraman and Sundaramoorthy [20] studied a single server Markovian queue with multiple working vacation and partial breakdown using matrix geometric method.In real world, many queueing situations arise in which there may be a tendency of customers to be discouraged by a long queue. Consequently, the customers either decide not to join the queue (balking) or depart after joining the queue without getting the service due to impatience (reneging). An 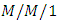 queue with impatient (balking and reneging) customers was first proposed by Haight [21,22] in the 1950s. Shawky [23] used the single-server machine interference model:
queue with impatient (balking and reneging) customers was first proposed by Haight [21,22] in the 1950s. Shawky [23] used the single-server machine interference model: 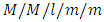 with balking, reneging and an additional server for longer queues under the consideration of first- in-first- out (FIFO) queueing discipline and he derived steady-state probabilities and measures of effectiveness in an explicit form. Yue et al. [24] analyzed customer’s impatience in an
with balking, reneging and an additional server for longer queues under the consideration of first- in-first- out (FIFO) queueing discipline and he derived steady-state probabilities and measures of effectiveness in an explicit form. Yue et al. [24] analyzed customer’s impatience in an 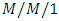 queueing system under server vacations, where they assumed that the ‘impatience timers’ of customers depend on the server’s states. Bouchentouf et al. [25] analyzed a finite capacity
queueing system under server vacations, where they assumed that the ‘impatience timers’ of customers depend on the server’s states. Bouchentouf et al. [25] analyzed a finite capacity 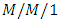 feedback queueing system with vacation and impatient customers and obtained measures of effectiveness of the model by using the stationary distribution. Laxmi et al. [26] dealt an infinite capacity single server Markovian queue with a single working vacation and reneging of customers due to working vacation. Yacov et al. [27] studied non-stationary Markov models of queueing systems with impatient customers. Very recently, Arizono and Takemoto [28] analyzed the steady-state distribution in
feedback queueing system with vacation and impatient customers and obtained measures of effectiveness of the model by using the stationary distribution. Laxmi et al. [26] dealt an infinite capacity single server Markovian queue with a single working vacation and reneging of customers due to working vacation. Yacov et al. [27] studied non-stationary Markov models of queueing systems with impatient customers. Very recently, Arizono and Takemoto [28] analyzed the steady-state distribution in 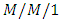 queueing system with balking based on the concept of statistical mechanics.There are some queues for which arrival and service rates depend on time which are known as transient queues. Abate and whitt [29] studied transient behavior of the
queueing system with balking based on the concept of statistical mechanics.There are some queues for which arrival and service rates depend on time which are known as transient queues. Abate and whitt [29] studied transient behavior of the 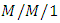 Queue: starting at the origin and presented some new perspectives on the time-dependent behavior of the queue. Al-Seedya et al. [30] studied transient solution of the
Queue: starting at the origin and presented some new perspectives on the time-dependent behavior of the queue. Al-Seedya et al. [30] studied transient solution of the 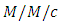 queue with balking and reneging and gave the transient probabilities of the queue size, by using the generating function technique and the properties of Bessel functions. Kaczynski et al. [31] combined the previous transient analysis results for
queue with balking and reneging and gave the transient probabilities of the queue size, by using the generating function technique and the properties of Bessel functions. Kaczynski et al. [31] combined the previous transient analysis results for 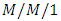 and
and 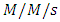 queues with the functionality of the Maple computational engine (and subsequently APPL) to develop both symbolic and numeric exact sojourn time PDFs that can be manipulated to compute and study various performance measures. Jain and Singh [32] investigated the transient model for a Markovian feedback queue with system disaster and customer impatient. Recently, Sampath et al. [33] analyzed an
queues with the functionality of the Maple computational engine (and subsequently APPL) to develop both symbolic and numeric exact sojourn time PDFs that can be manipulated to compute and study various performance measures. Jain and Singh [32] investigated the transient model for a Markovian feedback queue with system disaster and customer impatient. Recently, Sampath et al. [33] analyzed an 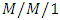 queueing system subjected to multiple differentiated vacations, customer impatience and a waiting server and they derived the explicit transient probabilities of system size using probability generating function technique, Laplace transform, continued fractions and some properties of confluent hypergeometric function.Batch (or bulk) arrival and service facility is another area of research in queueing theory. Krishnamoorthy and Ushakumari [34] studied a Markovian queueing system with accessible batches for service, but units depart individually and they computed various performance measures of the system. Ke and Wang [35] analyzed the operating characteristics for the heterogeneous batch arrival queue with server startup and breakdowns. They modeled the system by an
queueing system subjected to multiple differentiated vacations, customer impatience and a waiting server and they derived the explicit transient probabilities of system size using probability generating function technique, Laplace transform, continued fractions and some properties of confluent hypergeometric function.Batch (or bulk) arrival and service facility is another area of research in queueing theory. Krishnamoorthy and Ushakumari [34] studied a Markovian queueing system with accessible batches for service, but units depart individually and they computed various performance measures of the system. Ke and Wang [35] analyzed the operating characteristics for the heterogeneous batch arrival queue with server startup and breakdowns. They modeled the system by an 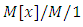 queue with server breakdowns and startup time under the N policy. Wang et al. [36] analyzed the
queue with server breakdowns and startup time under the N policy. Wang et al. [36] analyzed the 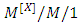 queueing system with multiple vacations and server breakdowns and they developed the approximate formulae for the probability distributions of the number of customers in the system using the maximum entropy principle. Xu et al. [37] studied a bulk input
queueing system with multiple vacations and server breakdowns and they developed the approximate formulae for the probability distributions of the number of customers in the system using the maximum entropy principle. Xu et al. [37] studied a bulk input 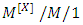 queue with single working vacation and derived the probability generating function of the stationary queue length distribution by matrix analysis method. Sometimes some customers are given preferential treatment in the sense that they can be served before those who came before them is defined as priority customers. Kao and Wilson [38] analyzed non- preemptive priority queues with multiple servers and two priority classes and developed the power-series formulation for the priority multi-server Markovian queues with two priority classes. Heijden et al. [39] discussed the approximation of performance measures in multi-class
queue with single working vacation and derived the probability generating function of the stationary queue length distribution by matrix analysis method. Sometimes some customers are given preferential treatment in the sense that they can be served before those who came before them is defined as priority customers. Kao and Wilson [38] analyzed non- preemptive priority queues with multiple servers and two priority classes and developed the power-series formulation for the priority multi-server Markovian queues with two priority classes. Heijden et al. [39] discussed the approximation of performance measures in multi-class 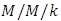 queues with preemptive priorities for large problem instances (many classes and servers) by using class aggregation and server reduction. Horváth et al. [40] studied a traffic based decomposition of two-class queueing networks with priority service and presented an approximate analysis approach for the networks. Retrial queues are an important field of study in queueing theory as, in various scenarios, they are able to capture certain behavior of real systems more accurately than classical first come first served queues. Artalejo and Falin [41] studied main models and results of retrial queues. They gave a survey of main results for both
queues with preemptive priorities for large problem instances (many classes and servers) by using class aggregation and server reduction. Horváth et al. [40] studied a traffic based decomposition of two-class queueing networks with priority service and presented an approximate analysis approach for the networks. Retrial queues are an important field of study in queueing theory as, in various scenarios, they are able to capture certain behavior of real systems more accurately than classical first come first served queues. Artalejo and Falin [41] studied main models and results of retrial queues. They gave a survey of main results for both 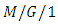 type and
type and 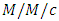 type retrial queues and discussed similarities and differences between the retrial queues and their standard counterparts. Roszik and Sztrik [42] dealt with the effect of server’s breakdown on the performance of finite-source
type retrial queues and discussed similarities and differences between the retrial queues and their standard counterparts. Roszik and Sztrik [42] dealt with the effect of server’s breakdown on the performance of finite-source 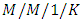 retrial queueing systems. They studied a finite-source homogeneous retrial queueing system with the novelty of the non–reliability of the server and derived the main performance and reliability measures. Phung-Duc [43] surveyed the main theoretical results for retrial queueing models and investigated retrial queueing models arising from real applications such as call centers, cellular networks, random access protocols etc.
retrial queueing systems. They studied a finite-source homogeneous retrial queueing system with the novelty of the non–reliability of the server and derived the main performance and reliability measures. Phung-Duc [43] surveyed the main theoretical results for retrial queueing models and investigated retrial queueing models arising from real applications such as call centers, cellular networks, random access protocols etc.3.2. Semi-Markovian Models
- Many researchers have contributed to the study of
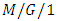 queueing models in different frameworks. Levy and Yechiali [13] studied an
queueing models in different frameworks. Levy and Yechiali [13] studied an 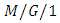 queueing model where the idle time of the server is utilized for additional work in a secondary system and they derived Laplace Stieltjes transforms of the occupation period, vacation period and waiting time for the model. Wu et al. [44] consideredan
queueing model where the idle time of the server is utilized for additional work in a secondary system and they derived Laplace Stieltjes transforms of the occupation period, vacation period and waiting time for the model. Wu et al. [44] consideredan 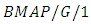 G-queues with second optional service and multiple vacations, by using the supplementary variables method and the censoring technique. Singh et al. [45] studied
G-queues with second optional service and multiple vacations, by using the supplementary variables method and the censoring technique. Singh et al. [45] studied 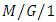 queueing model with state dependent arrival rates and vacation and they applied supplementary variable technique to determine the probability generating function of the queue size. Hur and Paik [46] studied an
queueing model with state dependent arrival rates and vacation and they applied supplementary variable technique to determine the probability generating function of the queue size. Hur and Paik [46] studied an 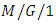 queue with general server setup time under the N- policy. Ke [47] investigated the control policy of the N policy
queue with general server setup time under the N- policy. Ke [47] investigated the control policy of the N policy 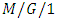 queue with server vacations, startup and breakdowns. Ke [48] studied the vacation policy of an
queue with server vacations, startup and breakdowns. Ke [48] studied the vacation policy of an 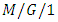 queueing system with an un- reliable server and startup. Using the analytical results, they derived the LSTs of various system characteristics for the modified T vacation policy
queueing system with an un- reliable server and startup. Using the analytical results, they derived the LSTs of various system characteristics for the modified T vacation policy 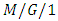 queueing system with an unreliable server and startup. Liu et al. [49] investigated an
queueing system with an unreliable server and startup. Liu et al. [49] investigated an 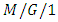 retrial G-queue with preemptive resume and feedback under N-policy vacation subject to the server breakdowns and repairs. Atencia and Moreno [50] considered a single-server
retrial G-queue with preemptive resume and feedback under N-policy vacation subject to the server breakdowns and repairs. Atencia and Moreno [50] considered a single-server 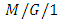 retrial queue with general retrial times and Bernoulli schedule and obtained analytical expressions for various performance measures of interest. Gao and Zhang [51] analyzed the performance of a hospital service system by modelling it as a continuous time
retrial queue with general retrial times and Bernoulli schedule and obtained analytical expressions for various performance measures of interest. Gao and Zhang [51] analyzed the performance of a hospital service system by modelling it as a continuous time 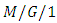 queue with retrial customers due to service vacation and derived various performance measures by using supplementary variable technique and transform methods. Woensel and Cruz [52] examined the optimal routing problem in arbitrary configured a cyclic queueing networks. Done and Whitt [53] investigated the consequences of fitting a birth and death process to a multi-server queue with a periodic time varying arrival rate function to better understanding of the system.Several researchers have attracted to the study of
queue with retrial customers due to service vacation and derived various performance measures by using supplementary variable technique and transform methods. Woensel and Cruz [52] examined the optimal routing problem in arbitrary configured a cyclic queueing networks. Done and Whitt [53] investigated the consequences of fitting a birth and death process to a multi-server queue with a periodic time varying arrival rate function to better understanding of the system.Several researchers have attracted to the study of 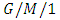 type queueing models. Li and Liu [54] analyzed a
type queueing models. Li and Liu [54] analyzed a 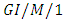 queue with vacations and multiple service phases and they obtained the distributions of the stationary system size at both arrival and arbitrary epochs by using the matrix geometric solution method and semi-Markov process. Also, they obtained the stationary waiting time distribution of an arbitrary customer and some important performance measures of the system. Yang and Cho [55] presented an algorithmic approach to the analysis of the finite capacity
queue with vacations and multiple service phases and they obtained the distributions of the stationary system size at both arrival and arbitrary epochs by using the matrix geometric solution method and semi-Markov process. Also, they obtained the stationary waiting time distribution of an arbitrary customer and some important performance measures of the system. Yang and Cho [55] presented an algorithmic approach to the analysis of the finite capacity 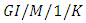 queueing system with working breakdowns and repairs under N-policy.Recently, Chydzinsky [56] analyzed the
queueing system with working breakdowns and repairs under N-policy.Recently, Chydzinsky [56] analyzed the 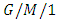 queueing model with the addition of the dropping function and proved the stability condition and accompanied with derivations of several steady-state and transient characteristics.Some researchers have studied and proposed some mathematical models of the types
queueing model with the addition of the dropping function and proved the stability condition and accompanied with derivations of several steady-state and transient characteristics.Some researchers have studied and proposed some mathematical models of the types 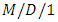 and
and 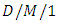 as well. Brun and Garcia [57] derived a closed-form formula for the distribution of the number of customers in the
as well. Brun and Garcia [57] derived a closed-form formula for the distribution of the number of customers in the 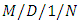 queueing system. They also gave an explicit solution for the mean queue length and the average waiting time. Seo [58] provided explicit formulae for a blocking probability, stationary distributions, and mean system sojourn times in
queueing system. They also gave an explicit solution for the mean queue length and the average waiting time. Seo [58] provided explicit formulae for a blocking probability, stationary distributions, and mean system sojourn times in 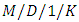 queues under two blocking policies: communication and production using max-plus algebra. Koth and Akhdar [59] derived the analytical solution in steady-state for
queues under two blocking policies: communication and production using max-plus algebra. Koth and Akhdar [59] derived the analytical solution in steady-state for 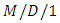 queue with balking, using iterative method and the probability generating function. Cosmetators and Prastacos [60] dealt an approximate analysis of the
queue with balking, using iterative method and the probability generating function. Cosmetators and Prastacos [60] dealt an approximate analysis of the 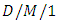 queue under deterministic customer impatience and obtained the probability of a customer reneging and the average service utilization. They also evaluated analytically the performance of the system in terms of these two measures.Some researchers are attracted to the study of
queue under deterministic customer impatience and obtained the probability of a customer reneging and the average service utilization. They also evaluated analytically the performance of the system in terms of these two measures.Some researchers are attracted to the study of 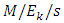 type queueing model in different frame works. Jain and Agrawal [61] investigated a state dependent
type queueing model in different frame works. Jain and Agrawal [61] investigated a state dependent 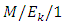 queueing system with server breakdown and working vacation. They derived several performance indices in explicit form by applying generating function approach. Zeng et al. [62] established a
queueing system with server breakdown and working vacation. They derived several performance indices in explicit form by applying generating function approach. Zeng et al. [62] established a 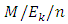 transient queueing model and optimization model to analyze and optimize the gate congestion according to the arrival time interval of the external container trucks and the distribution regularity of the service time for the rail way container terminal gate system. They applied the equally likely combinations heuristic solution and the optimization solution methods to solve the models.Many researchers have studied the semi-Markovian bulk queueing systems in different frameworks. Wang and Lu [63] studiedloss behavior in space priority queue with batch Markovian arrival process — continuous-time case and applied a matrix-analytic approach to analyze both the long-term and the short-term loss behaviors of the queue with space priority scheme. Sultan [64] introduced an easily applicable algorithm to solve problems involving bulk-arrival queues with a breakdown of one of the heterogeneous servers in case of steady state. He presented a Monte Carlo study for numerically finding the limiting distribution of the number in the system for the bulk arrival, multi-server queueing model
transient queueing model and optimization model to analyze and optimize the gate congestion according to the arrival time interval of the external container trucks and the distribution regularity of the service time for the rail way container terminal gate system. They applied the equally likely combinations heuristic solution and the optimization solution methods to solve the models.Many researchers have studied the semi-Markovian bulk queueing systems in different frameworks. Wang and Lu [63] studiedloss behavior in space priority queue with batch Markovian arrival process — continuous-time case and applied a matrix-analytic approach to analyze both the long-term and the short-term loss behaviors of the queue with space priority scheme. Sultan [64] introduced an easily applicable algorithm to solve problems involving bulk-arrival queues with a breakdown of one of the heterogeneous servers in case of steady state. He presented a Monte Carlo study for numerically finding the limiting distribution of the number in the system for the bulk arrival, multi-server queueing model 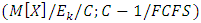 with heterogeneous servers. Park et al. [65] analyzed a single server, two-phase queueing system with batch policy of a fixed size and derived the steady state distribution for the system’s queue length and showed that the stochastic decomposition property can be applied to their model. Laxmi and Yesuf [66] analyzed a finite buffer single server accessible and non-accessible batch service queue with general input and Markovian service process. The supplementary variable and the embedded Markov chain techniques were used to obtain the steady state queue length distributions at pre-arrival and arbitrary epochs. The techniques used in this paper can be applied to analyze more complex models under batch arrival batch Markovian service process
with heterogeneous servers. Park et al. [65] analyzed a single server, two-phase queueing system with batch policy of a fixed size and derived the steady state distribution for the system’s queue length and showed that the stochastic decomposition property can be applied to their model. Laxmi and Yesuf [66] analyzed a finite buffer single server accessible and non-accessible batch service queue with general input and Markovian service process. The supplementary variable and the embedded Markov chain techniques were used to obtain the steady state queue length distributions at pre-arrival and arbitrary epochs. The techniques used in this paper can be applied to analyze more complex models under batch arrival batch Markovian service process 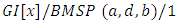 queue in both finite and infinite buffers.
queue in both finite and infinite buffers.3.3. Non-Markovian Models
- Many researchers have studied and proposed some mathematical models of the type
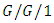 as well. Whitt [67] considered the
as well. Whitt [67] considered the 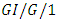 queue with minimizing delays and showed that for hyper-exponential inter-arrival time distributions, the service time distribution minimizing the average delay maximizes the proportion of customers delayed. Myskja [68] investigated the mean waiting time and queue length approximations for the
queue with minimizing delays and showed that for hyper-exponential inter-arrival time distributions, the service time distribution minimizing the average delay maximizes the proportion of customers delayed. Myskja [68] investigated the mean waiting time and queue length approximations for the 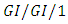 queueing model. Li and Niu [69] investigated a generalization of the
queueing model. Li and Niu [69] investigated a generalization of the 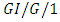 queue in which the server is turned off at the end of each busy period and is reactivated only when the sum of the service times of all waiting customers exceeds a given threshold of size D. Fiems et al. [70] analyzed a discrete-time
queue in which the server is turned off at the end of each busy period and is reactivated only when the sum of the service times of all waiting customers exceeds a given threshold of size D. Fiems et al. [70] analyzed a discrete-time 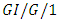 queueing model under bursty interruptions. Wu and Zhao [71] considered
queueing model under bursty interruptions. Wu and Zhao [71] considered 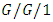 models for a single machine under different types of interruptions. Vazquez-Avila et al. [72] presented a fast simulation model for the performance analysis of the
models for a single machine under different types of interruptions. Vazquez-Avila et al. [72] presented a fast simulation model for the performance analysis of the 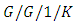 queue based on Lindley’s recursion. Very recently, Dieleman [73] dealt with the data-driven fitting of the
queue based on Lindley’s recursion. Very recently, Dieleman [73] dealt with the data-driven fitting of the 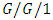 queue and used maximum likelihood estimation in combination with stochastic approximation to calibrate the arrival parameter of the queue via waiting time data.Some researchers are attracted to study the queueing models of the types
queue and used maximum likelihood estimation in combination with stochastic approximation to calibrate the arrival parameter of the queue via waiting time data.Some researchers are attracted to study the queueing models of the types 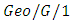 and
and 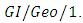 Lee et al. [74] dealt discrete-time
Lee et al. [74] dealt discrete-time 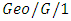 queues with disasters and general repairtimes. Li [75] investigated a discrete-time
queues with disasters and general repairtimes. Li [75] investigated a discrete-time 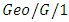 queueing system with multiple working vacations and analyzed the model using matrix analytic approach and the stochastic decomposition theory. Lee and Kim [76] studied discrete time
queueing system with multiple working vacations and analyzed the model using matrix analytic approach and the stochastic decomposition theory. Lee and Kim [76] studied discrete time 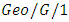 queues with negative customers and a repairable server. Jiang [77] analyzed a discrete time
queues with negative customers and a repairable server. Jiang [77] analyzed a discrete time 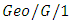 queue in a multi-phase service environment with disastrous breakdowns. Gao and Wang [78] analyzed a discrete time
queue in a multi-phase service environment with disastrous breakdowns. Gao and Wang [78] analyzed a discrete time 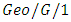 retrial queue with server vacation and two waiting buffers based on ATM networks by using the supplementary variable technique and the generating function approach. Chaudhry et al. [79] demonstrated analytically simple and computationally efficient results for the
retrial queue with server vacation and two waiting buffers based on ATM networks by using the supplementary variable technique and the generating function approach. Chaudhry et al. [79] demonstrated analytically simple and computationally efficient results for the 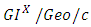 queueing models and they used the roots method to solve the model.Some researchers have contributed to the study of queueing models of the type
queueing models and they used the roots method to solve the model.Some researchers have contributed to the study of queueing models of the type 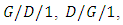 and
and 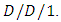 Schormans and Pitts [80] presented a new formula for calculating the decay rate in the
Schormans and Pitts [80] presented a new formula for calculating the decay rate in the 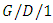 queue which has potential application in cell-based telecommunication systems, such as ATM. Ahn and Jeon [81] analyzed the
queue which has potential application in cell-based telecommunication systems, such as ATM. Ahn and Jeon [81] analyzed the 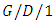 queueing models with inputs satisfying large deviation principle under weak topology. Balcioglu et al. [82] proposed an approximation for the mean waiting time of the
queueing models with inputs satisfying large deviation principle under weak topology. Balcioglu et al. [82] proposed an approximation for the mean waiting time of the 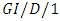 queue under auto correlated times to failures. Heckmuller and Wolfinger [83] proposed methods to estimate the parameters of arrival processes to
queue under auto correlated times to failures. Heckmuller and Wolfinger [83] proposed methods to estimate the parameters of arrival processes to 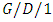 queueing models only based on observed departures from the system. Servi [84] analyzed a
queueing models only based on observed departures from the system. Servi [84] analyzed a 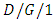 queue with vacations and investigated various performance measures. Racz et al. [85] considered the
queue with vacations and investigated various performance measures. Racz et al. [85] considered the 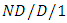 queueing system and obtained the exact distribution of the cumulative idle time duration in such queueing systems. They also proposed accurate approximation formulae for large systems.
queueing system and obtained the exact distribution of the cumulative idle time duration in such queueing systems. They also proposed accurate approximation formulae for large systems.4. Solution Techniques of Various Queueing Models
- Various techniques have been introduced by many researchers to analyze the Markovian queueing models. Some of their techniques include thebirth-and-death process, generating function (probability generating function) method, GJL algorithm, iterative method, Runge-Kutta method, Laplace transform, Laplace Stieltjes transform, matrix analytic method (matrix-geometric method), maximum entropy principle, Markov process, MOSEL (Modelling Specification and Evaluation Language) tool, Monte Carlo simulation, Bessel functions, Quasi-birth-death process, recursive method, Particle Swarm algorithm (for optimization), Direct Search method and Quasi-Newton method (for optimization).The solution techniques for semi-Markovian queueing models are embedded Markov-chain technique, generating function (probability generating function)technique, matrix geometric solution technique (matrix analytic approach), supplementary variable technique, stochastic decomposition property technique, semi-Markov process, maximum entropy approach, Pollaczek-Khinchin formula, censoring method, addition of dropping function method, level crossing analysis method, communication or production blocking policy method, finite truncation method, known approximate performance evaluation method etc.Some of the techniques to analyze the non-Markovian queueing models include the generating function, matrix-geometric, Lindley’s recursion, max-plus algebra, imbedded Markov chain, supplementary variable, semi-Markov process, birth-and-death process, combinatorial and numerical methods, roots method.Most of the parameters we take into account under the study of queueing systems exhibit stochastic process due to which the variables we denote are random variables such as arrival rate, service rate, reneging rate, balking rate, failure rate, resource sharing rate.
5. Performance Measures of Some of Markovian, Semi-Markovian and Non-Markovian Queueing Systems
- Let
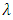 = mean arrival rate,
= mean arrival rate, 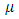 = mean service rate,
= mean service rate, 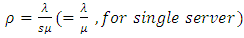
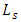 = expectednumber of customers in the system
= expectednumber of customers in the system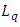 = expected number of customers in the queue
= expected number of customers in the queue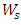 = expected time spent in the system
= expected time spent in the system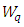 = expected time spent in the queue
= expected time spent in the queue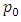 = probability of having zero customers in the system
= probability of having zero customers in the system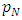 = probability of having
= probability of having 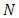 customers in the system
customers in the system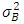 = variance of the service distributionThen the results of
= variance of the service distributionThen the results of 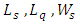 and
and 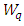 for various queueing systems has been tabulated as follows:
for various queueing systems has been tabulated as follows:
|
|
6. Applications of Various Queueing Models
- There are countless and diverse applications of Markovian queueing models in real life situations such as in the area of Computer networks, communication traffic (mobile, telephone, telegraph, post office), transportation traffic (land, sea, air), hospital and medical-care-facility congestions, inventories and industrial process (maintenance, assembly lines, machine interference), manufacturing and production systems, quality control problems, distribution systems, ATM service, tool booths, software architecture, load balancing in multiprotocol label switching networks, Ethernet systems, wireless broadband networks, active queue management of internet routers, self-organizing peer-to-peer systems, the dynamical host configuration protocol, internet protocol access network, circuit designing internet service and many other areas.
7. Conclusions
- A survey in Markovian, semi-Markovian and non-Markovian queueing systems has been made so as to give insight into its pioneering to its advancement. Some of the queueing- policies which have been used in various situations have been illustrated with their pioneers. The up to date development of the queueing system reported in the survey will enable the reader to get knowledge in a bird’s eye-view.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
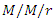 queueing system with queue-dependent servers, Computers and Mathematics with Applications, 50(2005), 187-199.
queueing system with queue-dependent servers, Computers and Mathematics with Applications, 50(2005), 187-199.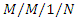 queueing system cost model in a vague environment, International Journal of Fuzzy Logic and Intelligent Systems, 19(3) (2019), 192-203.
queueing system cost model in a vague environment, International Journal of Fuzzy Logic and Intelligent Systems, 19(3) (2019), 192-203.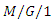 queueing system, Management Science, 22(2) 1975, 202-211 https://doi.org/10.1287/mnsc.22.2.202.
queueing system, Management Science, 22(2) 1975, 202-211 https://doi.org/10.1287/mnsc.22.2.202.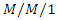 queues with working vacations
queues with working vacations 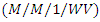 , Performance Evaluation, 50(1)(2002), 41-52.
, Performance Evaluation, 50(1)(2002), 41-52.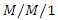 queue with working vacations, Operations Research Letters, 35(5)(2007), 595-600.
queue with working vacations, Operations Research Letters, 35(5)(2007), 595-600.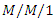 multiple vacation queueing systems with differentiated vacations, Modeling and Simulation in Engineering, 2014(2014), 1-6, Article ID 158247.
multiple vacation queueing systems with differentiated vacations, Modeling and Simulation in Engineering, 2014(2014), 1-6, Article ID 158247.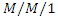 queues with working vacations and vacation interruptions, Mathematical Problems in Engineering, 2016 (2016), 1-10, Article ID 9746962, http://dx.doi.org/10.1155/2016/9746962.
queues with working vacations and vacation interruptions, Mathematical Problems in Engineering, 2016 (2016), 1-10, Article ID 9746962, http://dx.doi.org/10.1155/2016/9746962.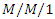 queueing system with balking based on concept of statistical mechanics, RAIRO Operations Research, 55 (2021), S327-S341.
queueing system with balking based on concept of statistical mechanics, RAIRO Operations Research, 55 (2021), S327-S341.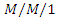 queue: starting at the origin, Queueing system, 2(1987), 41-65.
queue: starting at the origin, Queueing system, 2(1987), 41-65.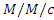 queue with balking and reneging, Computers and Mathematics with Applications, 57(2010), 1280-1285.
queue with balking and reneging, Computers and Mathematics with Applications, 57(2010), 1280-1285.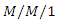 queueing system subjected to multiple differentiated vacations, impatient customers and a waiting server with applications to IEEE 802.16E power sharing mechanism, Indian Journal of Pure and Applied Mathematics, 51 (2020), 297-320.
queueing system subjected to multiple differentiated vacations, impatient customers and a waiting server with applications to IEEE 802.16E power sharing mechanism, Indian Journal of Pure and Applied Mathematics, 51 (2020), 297-320.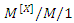 queueing system with multiple vacations and server breakdowns, Computers and Industrial Engineering, 52(2) (2007), 192-202.
queueing system with multiple vacations and server breakdowns, Computers and Industrial Engineering, 52(2) (2007), 192-202.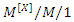 working vacation queue, International Journal of Information and Management Sciences, 20(2009), 379-394.
working vacation queue, International Journal of Information and Management Sciences, 20(2009), 379-394.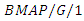 G-queues with second optimal service and multiple vacations, Applied Mathematical Modeling, 33(12)(2009), 4314-4325.
G-queues with second optimal service and multiple vacations, Applied Mathematical Modeling, 33(12)(2009), 4314-4325.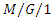 queueing model with state dependent arrival and vacation, Journal of Industrial Engineering International, 8(2) (2012), 1-8.
queueing model with state dependent arrival and vacation, Journal of Industrial Engineering International, 8(2) (2012), 1-8.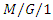 with server setup, Applied Mathematical Modeling, 23(4)(1999), 289-299.
with server setup, Applied Mathematical Modeling, 23(4)(1999), 289-299.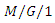 queueing system with server vacations, startup and breakdowns, Computers and Industrial Engineering, 44(4)(2003), 567-579.
queueing system with server vacations, startup and breakdowns, Computers and Industrial Engineering, 44(4)(2003), 567-579.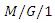 queueing system with an unreliable server and startup, Mathematical and Computer Modeling, 41(2005), 1267-1277.
queueing system with an unreliable server and startup, Mathematical and Computer Modeling, 41(2005), 1267-1277.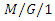 retrial G- queue with preemptive resume and feedback under N-policy subject to the server breakdowns and repairs, Computers and Mathematics with Applications, 58(9)(2009), 1792-1807.
retrial G- queue with preemptive resume and feedback under N-policy subject to the server breakdowns and repairs, Computers and Mathematics with Applications, 58(9)(2009), 1792-1807.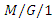 queue with retrial customers due to server vacation, Ain Shams Engineering Journal, 11(3) (2020), 795-803.
queue with retrial customers due to server vacation, Ain Shams Engineering Journal, 11(3) (2020), 795-803.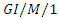 queue with vacations and multiple service phases, Mathematical Problems in Engineering, 2017 (2017), 14 pages, Article ID 3246934 https://doi.org/10.1155/2017/3246934.
queue with vacations and multiple service phases, Mathematical Problems in Engineering, 2017 (2017), 14 pages, Article ID 3246934 https://doi.org/10.1155/2017/3246934.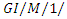 queueing system with working breakdowns and re pairs, The Computer Journal, 62(1) (2019), 130-143.
queueing system with working breakdowns and re pairs, The Computer Journal, 62(1) (2019), 130-143.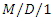 queues, Journal of Applied Probability, 37(4) (2000), 1092-1098 DOI: https://doi.org/10.1239/jap/1014843086.
queues, Journal of Applied Probability, 37(4) (2000), 1092-1098 DOI: https://doi.org/10.1239/jap/1014843086.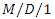 queues, ETRI Journal, 36(4) (2014), 609-616.
queues, ETRI Journal, 36(4) (2014), 609-616.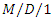 with balking, Applied and Computational Mathematics, 7(2) (2018), 31-39.
with balking, Applied and Computational Mathematics, 7(2) (2018), 31-39.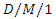 queue with deterministic customer impatience, RAIRO Operations Research, 19 (2) (1985), 133-142.
queue with deterministic customer impatience, RAIRO Operations Research, 19 (2) (1985), 133-142.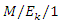 queueing system with working vacation, Quality Technology and Quantitative Management, 4(4) (2007), 455-470.
queueing system with working vacation, Quality Technology and Quantitative Management, 4(4) (2007), 455-470.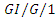 queue, Operations Research, 32 (1) (1984), 41-51.
queue, Operations Research, 32 (1) (1984), 41-51.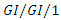 queue, Computer Networks and ISDN Systems, 20 (1-5) (1990), 285-295.
queue, Computer Networks and ISDN Systems, 20 (1-5) (1990), 285-295.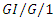 queue under the D-policy, Probability in the Engineering and Informational Sciences, 6 (1992), 287-308.
queue under the D-policy, Probability in the Engineering and Informational Sciences, 6 (1992), 287-308.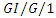 queueing model subject to bursty interruptions, Computers and Operations Research, 30(1) (2003), 139-153.
queueing model subject to bursty interruptions, Computers and Operations Research, 30(1) (2003), 139-153.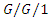 models for a single machine under different types of interruptions, IEEE International Conference on Industrial Engineering and Engineering Management, 2013, DOI: 10.1109/IEEM.2013.6962376.
models for a single machine under different types of interruptions, IEEE International Conference on Industrial Engineering and Engineering Management, 2013, DOI: 10.1109/IEEM.2013.6962376.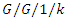 queue, Mathematical Problems in Engineering, 2019 (2019), 11 pages, Article ID 3464389 https://doi.org/10.1155/2019/3464389.
queue, Mathematical Problems in Engineering, 2019 (2019), 11 pages, Article ID 3464389 https://doi.org/10.1155/2019/3464389.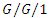 queue, Journal of Systems Science and Systems Engineering, 30 (2021), 17-28.
queue, Journal of Systems Science and Systems Engineering, 30 (2021), 17-28.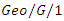 queues with disasters and general repair times, Applied Mathematical Modeling, 35(4) (2011), 1561-1570.
queues with disasters and general repair times, Applied Mathematical Modeling, 35(4) (2011), 1561-1570.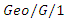 working vacation queue and its application to network scheduling, Computers and Industrial Engineering, 65(2013), 594-604.
working vacation queue and its application to network scheduling, Computers and Industrial Engineering, 65(2013), 594-604.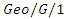 queues with negative customers, Journal of Applied Mathematics, 2014 (2014), 1-10, Article ID 350621.
queues with negative customers, Journal of Applied Mathematics, 2014 (2014), 1-10, Article ID 350621.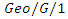 queue in a multi-phase service environment with disasters, Journal of Systems Science and Information, 6(4) (2018), 349-365.
queue in a multi-phase service environment with disasters, Journal of Systems Science and Information, 6(4) (2018), 349-365.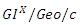 queues, Journal of Probability and Statistics, 2019 (2019), 18 pages, Article ID 6480139, https://doi.org/I0.1155/2019/6480139.
queues, Journal of Probability and Statistics, 2019 (2019), 18 pages, Article ID 6480139, https://doi.org/I0.1155/2019/6480139.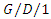 queue and results for ATM telecommunications, Electronics Letters, 34(10) (1998), 943-945. DOI: 10.1049/el: 19980741.
queue and results for ATM telecommunications, Electronics Letters, 34(10) (1998), 943-945. DOI: 10.1049/el: 19980741.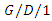 queueing systems with inputs satisfying large deviation principle under weak topology, Queueing Systems, 40(2002), 295-311.
queueing systems with inputs satisfying large deviation principle under weak topology, Queueing Systems, 40(2002), 295-311.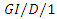 queue with auto correlated times of failures, IIE Transactions, 39 (10) (2007), 985-996.
queue with auto correlated times of failures, IIE Transactions, 39 (10) (2007), 985-996.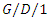 queueing systems and tendem networks, IEEE, 2009, https//ieeerplore.ieee.org/document/5224100.
queueing systems and tendem networks, IEEE, 2009, https//ieeerplore.ieee.org/document/5224100.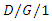 queues with vacations, Operations Research, 34(4) (1986) https://doi.org/10.1287/opre.34.4.619.
queues with vacations, Operations Research, 34(4) (1986) https://doi.org/10.1287/opre.34.4.619.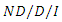 queue, Queueing Systems, 49 (2005), 297-319.
queue, Queueing Systems, 49 (2005), 297-319.