American Journal of Computational and Applied Mathematics

p-ISSN: 2165-8935    e-ISSN: 2165-8943

2021;  11(1): 18-19

doi:10.5923/j.ajcam.20211101.03

Received: Mar. 6, 2021; Accepted: Mar. 26, 2021; Published: Apr. 3, 2021

 

On One Scheme of Singular Integrals Approximate Calculation and on Its Use

D. Bitsadze

Department of Mathematics, Georgian Technical University, Tbilisi, Georgia

Correspondence to: D. Bitsadze, Department of Mathematics, Georgian Technical University, Tbilisi, Georgia.

Email:

Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.

This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract

The article deals with construction of one specific scheme for approximate calculation of singular integrals and its use for numerical solutions of integral equations of some class in the sense of Cauchy principal value. Composed quadrature formulas makes it possible equal assessment for quite a wide variety of smooth closed contours.

Keywords: Integral, Continuity model, Liapunov curve, Singular integral equation

Cite this paper: D. Bitsadze, On One Scheme of Singular Integrals Approximate Calculation and on Its Use, American Journal of Computational and Applied Mathematics , Vol. 11 No. 1, 2021, pp. 18-19. doi: 10.5923/j.ajcam.20211101.03.

Article Outline

1. Introduction
2. Main Body
3. Conclusions

1. Introduction

Numerous problems of mathematics, physics, and mechanics are reduced to singular integral equations [1] that predetermines much attention to the issues of numerical solution of the mentioned equations. In its turn, it is natural that the one or another approximate solution scheme for such equation may be constructed based exactly on the approximate calculation schemes of singular integrals with a Cauchy kernel. Thus, in addition to the fact that the mentioned integrals represent in themselves the interesting and attractive mathematical object, the development of the approximate solution methods for equations consisting of such integrals is of considerable interest, as well.
The following main notation is used in the work: L is the oriented contour on the plane; C(L) denotes the class of functions continuous on L with a norm 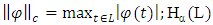denotes the class of Hölder functions on L with an exponent 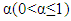and a norm 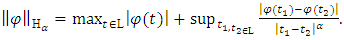besides,
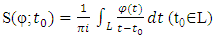(1)

2. Main Body

Let us assume that 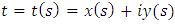is a parametric equation of some, sufficiently smooth, closed L contour referred to arc abscisse 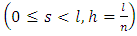. We select two 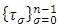and 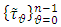systems of nodes on L as follows: 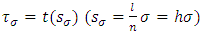divides L into 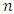equal parts (according to arc length), while 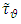point is a midpoint of 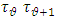arc. We assume that
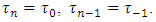Denote
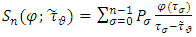(2)
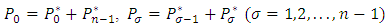where and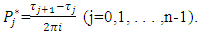
The following theorem is proved:
if 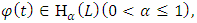then the following estimation takes place
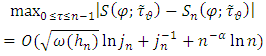(3)
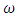where denotes the biggest among modules of continuity of functions 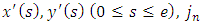is some sequence of natural numbers, satisfying the conditions 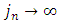and 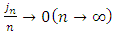. For any natural 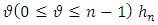denotes the length of that 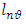arc, which has endpoints 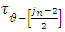and 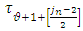, midpoint 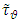, consists of exactly 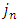nodes and 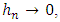when 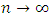so that 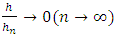. At that, the constant entering the right side of (3) depends on Hölder constant of function .
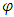The mentioned estimation is fair for any smooth, closed contour. In case, when 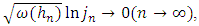the process is uniformly convergent for any 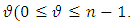If we assume that 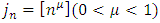and L is a Liapunov curve with some exponent 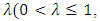the estimation (3) converts into the following .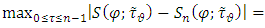
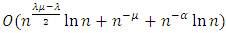The considered scheme may be used for numerical solution of singular integral equations of I kind, in particular for the following equation
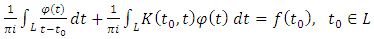(4)
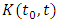Here L is a closed, smooth Liapunov curve, while and 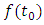are Hölder class functions given on L. We associate (4) with the system of linear algebraic equations
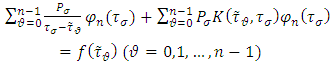(5)
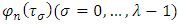It is proved that starting with certain n, the system (5) is unambiguously solvable and values uniformly converge to the solution corresponding with (4).

3. Conclusions

There are composed quadrature formulas, which enable us to give an equal assessment for quite wide class of smooth closed L contours, in contradistinction from the cases of similar schemes considered by other authors [2], [3], when an integrable curve is either a segment or a circle.
As for the scheme application in approximate solutions of singular integral equations, the following circumstance should be noted: a considered approximate scheme, which can lay a foundation for approximation of singular equation with Cauchy kernel, according to known terminology, is ranked among direct calculation schemes, use of which in practice for numerical solutions is much easier, than of those schemes, which are based on equivalent regularization of singular equations (reduction to Fredholm equation).

References

[1]  Muskhelishvili N.I. “Singulyarnye integralnye uravnenia” (Singular Integral Equations), M., “Nauka”, 1968.
[2]  Belotserkovsky S.M., Lifanov I.K. “Chislennye metody v singulyarnykh integralnykh uravneniakh” (Numerical methods in singular integral equations), M., “Nauka”, 1985.
[3]  Pykhteev G.N. “O postroenii kvadraturnykh formul dlya integralov tipa Koshi po pryamolineinomu razomknutomu konturu” (On construction of quadrature formula for Cauchy type integrals on rectangular open contour). Heralds of Academy of Sciences of BSSR, series of phys.-math. sciences, N2, 1970.
[4]  Nikolsky S.M. “Kvadraturnye formuly” (Quadrature formulas), M., 1988.
[5]  Bitsadze D.G., Sanikidze D.G. “O chislennom reshenii nekotorykh singulyarnykh integralnykh uravnenij” (On numerical solution of some singular integral equations). Abstracts of the conference “Effective numerical methods for solution of boundary problems of deformable solid body mechanics”, Kharkov, p.28. 1989.
[6]  Bitsadze D.G. On some questions of approximation and application of singular integrals with Cauchy kernel. Continuum Mechanics and Related Problems of Analysis Symposium Dedicated to the Centenary of Academician N. Muskhelishvili, Tbilisi, p. 68, 1991.
[7]  Erdogan F.E., Gypta G.D., “On the numerical solution of singular integral equations”. Quarterly of Applied Mathematics, 29, N4, 1972.