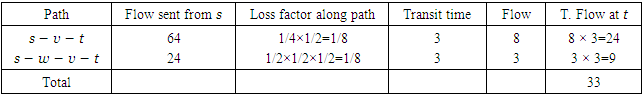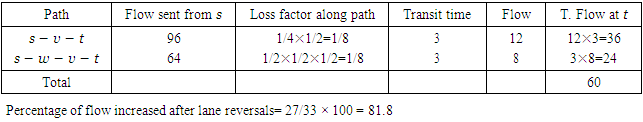-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2021; 11(1): 12-17
doi:10.5923/j.ajcam.20211101.02
Received: Feb. 2, 2021; Accepted: Mar. 15, 2021; Published: Mar. 15, 2021

Generalized Dynamic Contraflow with Non-Symmetric Transit Times
Shiva Prakash Gupta1, Urmila Pyakurel2, Tanka Nath Dhamala2
1Tribhuvan University, Tri-Chandra Multiple Campus, Kathmandu, Nepal
2Central Department of Mathematics, Tribhuvan University, Kathmandu, Nepal
Correspondence to: Urmila Pyakurel, Central Department of Mathematics, Tribhuvan University, Kathmandu, Nepal.
| Email: | 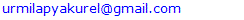 |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In a transportation network such as an evacuation planning, if we transmit the people or goods from the dangerous zones to the safety places, there are chances of loss due to death, leakage or damage. To address this issue, the generalized network flow model incorporates a gain factor on each arc, which makes it different from the classical network flow problems. The lane reversal strategy improves both flow value and also minimize the time with minimum loss. In general, the generalized dynamic contraflow problem is NP-hard, whereas, in a lossy network with symmetric transit time on anti-parallel arcs, it is solved in pseudo-polynomial time. Due to an uneven road network structure, transit time on arcs may be asymmetrical. We extend the analytical solution of generalized dynamic contraflow problem to the case of asymmetric transit time on arcs, both in discrete and continuous-time settings, and present efficient algorithms to solve it within the same complexity.
Keywords: Evacuation network, Network flow, Generalized dynamic flow, Lossy network, Contraflow
Cite this paper: Shiva Prakash Gupta, Urmila Pyakurel, Tanka Nath Dhamala, Generalized Dynamic Contraflow with Non-Symmetric Transit Times, American Journal of Computational and Applied Mathematics , Vol. 11 No. 1, 2021, pp. 12-17. doi: 10.5923/j.ajcam.20211101.02.
Article Outline
1. Introduction
- In the 1950s, Ford and Fulkerson [6,7] introduced the notion of dynamic flow problem by incorporating time component and provided the polynomial-time solution to the maximum flow problem. By using natural transformation Fleischer and Tardos [5] extended dynamic flow solutions into a continuous-time setting within the same time complexity.The classical network flow problem is generalized by associating a flow multiplier (gain or loss factors)
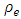 to each arc
to each arc 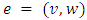 that modifies the flow, i.e., if one unit of flow enters on the arc at node
that modifies the flow, i.e., if one unit of flow enters on the arc at node 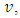 then
then 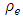 units arrive at node
units arrive at node 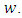 The generalized network is classified as a lossy network, if
The generalized network is classified as a lossy network, if 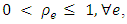 and a network with gain, if
and a network with gain, if 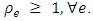 It coincides with the classical network, if
It coincides with the classical network, if 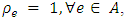 where
where 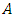 represents the set of arcs in the network. Jewell [13] introduced the generalized flow problem, wherein the objective is to maximize the flow from the origin (source node) to the destination (sink node) with minimum loss. The first exponential-time augmenting path algorithms for generalized maximum static flow problem were presented in [13,16]. Authors in [8] designed the first polynomial-time combinatorial algorithm for it. The relationship of this problem to the minimum cost flow problem was stated by Truemper [28]. The static flow problem is polynomial-time solvable, but in general, the dynamic flow problem is NP-hard [10,11].Contraflow or lane reversals is an approach designed to expand the capacity of the lanes to increase the flow in the direction of destination nodes by switching the orientation of unoccupied road segments [3,27]. Various contraflow problems in discrete and continuous-time have been investigated by the authors in [4,15,19,20,21,22,23,24,26]. There has been much more work on multi-commodity contraflow problems in [2,12,25]. In all these problems author assumed that capacity is non-symmetric, but transit time is symmetric on anti-parallel arcs. This assumption is no longer true for the uneven road network in urban areas due to ascent and descent of anti-parallel arcs and flow and time dependency. So, transit time may not be symmetric in contraflow configuration.Bhandari and Khadka [1] consider the maximum dynamic contraflow problem with non-symmetric transit times on anti-parallel arcs but the reversals use the symmetric transit times. Nath et al. [14] solved it by modifying the algorithm of [27] such that the reversals use asymmetric transit times that should be taken by unreserved ones. We extend the approach of Nath et al. [14] and introduce the maximum GDPCF problems in the discrete and continuous-time settings with non-symmetric transit times on anti-parallel arcs and solved them in pseudo-polynomial time complexity.The paper is organized as follows. Section 2 represents the basic terminologies with different flow models. We introduce the GDPCF problem with non-symmetric transit time on anti-parallel arcs and present pseudo-polynomial time algorithms with discrete and continuous time settings in Section 3 and Section 4, respectively. Section 5 concludes the paper.
represents the set of arcs in the network. Jewell [13] introduced the generalized flow problem, wherein the objective is to maximize the flow from the origin (source node) to the destination (sink node) with minimum loss. The first exponential-time augmenting path algorithms for generalized maximum static flow problem were presented in [13,16]. Authors in [8] designed the first polynomial-time combinatorial algorithm for it. The relationship of this problem to the minimum cost flow problem was stated by Truemper [28]. The static flow problem is polynomial-time solvable, but in general, the dynamic flow problem is NP-hard [10,11].Contraflow or lane reversals is an approach designed to expand the capacity of the lanes to increase the flow in the direction of destination nodes by switching the orientation of unoccupied road segments [3,27]. Various contraflow problems in discrete and continuous-time have been investigated by the authors in [4,15,19,20,21,22,23,24,26]. There has been much more work on multi-commodity contraflow problems in [2,12,25]. In all these problems author assumed that capacity is non-symmetric, but transit time is symmetric on anti-parallel arcs. This assumption is no longer true for the uneven road network in urban areas due to ascent and descent of anti-parallel arcs and flow and time dependency. So, transit time may not be symmetric in contraflow configuration.Bhandari and Khadka [1] consider the maximum dynamic contraflow problem with non-symmetric transit times on anti-parallel arcs but the reversals use the symmetric transit times. Nath et al. [14] solved it by modifying the algorithm of [27] such that the reversals use asymmetric transit times that should be taken by unreserved ones. We extend the approach of Nath et al. [14] and introduce the maximum GDPCF problems in the discrete and continuous-time settings with non-symmetric transit times on anti-parallel arcs and solved them in pseudo-polynomial time complexity.The paper is organized as follows. Section 2 represents the basic terminologies with different flow models. We introduce the GDPCF problem with non-symmetric transit time on anti-parallel arcs and present pseudo-polynomial time algorithms with discrete and continuous time settings in Section 3 and Section 4, respectively. Section 5 concludes the paper.2. Mathematical Formulations of Flow Models
- Let us consider a generalized dynamic network
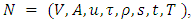 where
where 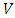 is the set of
is the set of 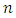 nodes, and
nodes, and 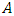 is the set of
is the set of 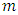 arcs. The capacity function
arcs. The capacity function  limits the flow and transit time function
limits the flow and transit time function 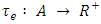 measures the arc traversal time. The function
measures the arc traversal time. The function 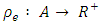 on arc e, is the gain function. The sets of outgoing arcs from node v and incoming arcs to node v are denoted by
on arc e, is the gain function. The sets of outgoing arcs from node v and incoming arcs to node v are denoted by 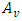 and
and 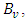 respectively. For a network
respectively. For a network 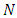 , the auxiliary network is denoted by
, the auxiliary network is denoted by 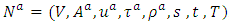 , with undirected edges in
, with undirected edges in 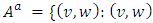 or
or 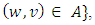 where
where 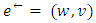 is the reversed arc of
is the reversed arc of  . The capacity of the auxiliary arc is the sum of capacities of arcs
. The capacity of the auxiliary arc is the sum of capacities of arcs 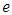 and
and 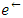 such that
such that 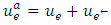 where
where 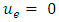 if
if 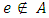 . The transit time of auxiliary arc
. The transit time of auxiliary arc 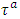 is
is 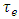 if arc
if arc 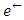 is reversed in the direction of arc e and
is reversed in the direction of arc e and 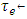 if arc e is reversed in the direction of
if arc e is reversed in the direction of 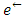 . In the case of a one-way road network between two nodes, we assume that
. In the case of a one-way road network between two nodes, we assume that 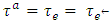 for contraflow configuration. Other network parameters are unaltered.Generalized dynamic flow with lane reversals. A generalized discrete dynamic flow
for contraflow configuration. Other network parameters are unaltered.Generalized dynamic flow with lane reversals. A generalized discrete dynamic flow 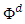 is defined by the function
is defined by the function 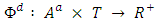 for given time T satisfying the constraints (1-3).
for given time T satisfying the constraints (1-3).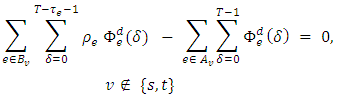 | (1) |
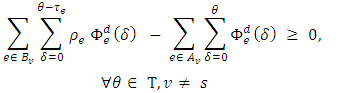 | (2) |
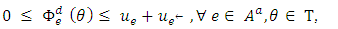 | (3) |
 in (4)
in (4)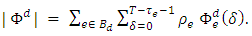 | (4) |
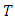 is denoted by
is denoted by 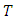 = {0, 1, …, T − 1} in discrete and
= {0, 1, …, T − 1} in discrete and 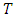 = [0, T) in continuous-time settings. Also, the maximum generalized static flow problem has an analogous formulation by dropping out the time parameters in constraints (1-3) and the objective function (4), respectively.A generalized continuous dynamic flow
= [0, T) in continuous-time settings. Also, the maximum generalized static flow problem has an analogous formulation by dropping out the time parameters in constraints (1-3) and the objective function (4), respectively.A generalized continuous dynamic flow 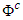 is defined by
is defined by 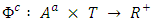 , where
, where 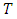 = [0, T). The capacity constraint, flow conservation constraints, and the objective function is similar, as (1-4), with the sum over time replaced by an integral.Residual network. The residual network
= [0, T). The capacity constraint, flow conservation constraints, and the objective function is similar, as (1-4), with the sum over time replaced by an integral.Residual network. The residual network 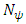 of network
of network 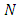 has the same number of nodes as in the network
has the same number of nodes as in the network 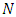 and each edge of network
and each edge of network 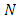 corresponds to two edges in the residual network
corresponds to two edges in the residual network 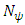 . The capacity of arcs in the residual network is defined by
. The capacity of arcs in the residual network is defined by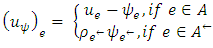 The transit times and gain factors are extended to the reverse edges on the residual network as follows
The transit times and gain factors are extended to the reverse edges on the residual network as follows 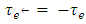 and
and  for all
for all 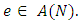 Time expanded network. To solve the discrete dynamic flow problem authors in [6] introduced time expanded network. It is extended to solve generalized dynamic flow problem in [11], by introducing static time expanded network
Time expanded network. To solve the discrete dynamic flow problem authors in [6] introduced time expanded network. It is extended to solve generalized dynamic flow problem in [11], by introducing static time expanded network 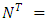
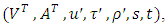 where
where 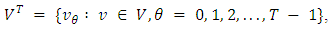
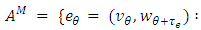
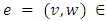
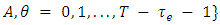 , and
, and 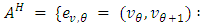
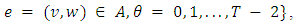 with
with 
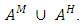 Capacity and loss factor on time expanded network are, respectively, defined by
Capacity and loss factor on time expanded network are, respectively, defined by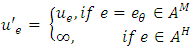 and
and 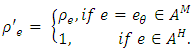 Based on Ford and Fulkerson [6,7], Gross and Skutella [11] formalize the relation of generalized flow over time in the static network and static flows in the time-expanded network. They prove Lemma 1.Lemma 1. Let
Based on Ford and Fulkerson [6,7], Gross and Skutella [11] formalize the relation of generalized flow over time in the static network and static flows in the time-expanded network. They prove Lemma 1.Lemma 1. Let 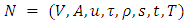 be a generalized dynamic network with integral transit time. For any time horizon T, a feasible generalized static flow in the time-expanded network
be a generalized dynamic network with integral transit time. For any time horizon T, a feasible generalized static flow in the time-expanded network 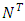 yields the same amount of generalized flow over time to the sink in the network
yields the same amount of generalized flow over time to the sink in the network 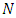 and vice-versa.A single-source single-sink flow can be decomposed into paths and cycles. In the same way, generalized static flow can be decomposed into paths and cycles due to Gondran and Minoux [9]. Onaga [16,17] provided an optimality criterion for the maximum generalized flow problem and proved Theorem 1.Theorem 1. A generalized flow ψ in a network
and vice-versa.A single-source single-sink flow can be decomposed into paths and cycles. In the same way, generalized static flow can be decomposed into paths and cycles due to Gondran and Minoux [9]. Onaga [16,17] provided an optimality criterion for the maximum generalized flow problem and proved Theorem 1.Theorem 1. A generalized flow ψ in a network 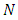 is a maximum generalized flow if, in the residual network
is a maximum generalized flow if, in the residual network 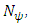 there is neither an
there is neither an 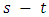 flow augmenting path nor a flow generating cycle.
flow augmenting path nor a flow generating cycle.3. Discrete GDPCF on Lossy Network with Asymmetric Transit Times
- The maximum generalized dynamic flow problem for single-commodity on the lossy network is solved by Gross and Skutella [11]. The authors in [19] introduce the contraflow strategy and provide an optimal solution with asymmetric capacity and symmetric transit time on arcs. We extend this idea in the case of asymmetric transit times on arcs and introduce Problem 1. Problem 1. Consider a lossy network
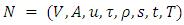 with proportional loss factor on each arc, i.e.,
with proportional loss factor on each arc, i.e., 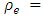
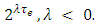 The maximum GDPCF problem on a lossy network with asymmetric capacities and transit times on arcs is to obtain the maximum amount of flow that can be sent from
The maximum GDPCF problem on a lossy network with asymmetric capacities and transit times on arcs is to obtain the maximum amount of flow that can be sent from  with a minimum loss if the direction of arcs can be reversed at zero processing cost.To solve Problem 1, we present Algorithm 1.Algorithm 1: The GDPCF Algorithm with Non-Symmetric Arc ParametersInput: Given generalized dynamic lossy network
with a minimum loss if the direction of arcs can be reversed at zero processing cost.To solve Problem 1, we present Algorithm 1.Algorithm 1: The GDPCF Algorithm with Non-Symmetric Arc ParametersInput: Given generalized dynamic lossy network 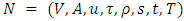 with constant and non-symmetric transit time on arcsOutput: The maximum GDPCF1. The given network
with constant and non-symmetric transit time on arcsOutput: The maximum GDPCF1. The given network 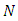 is transformed into the auxiliary network
is transformed into the auxiliary network 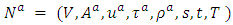 by adding two-way capacities as
by adding two-way capacities as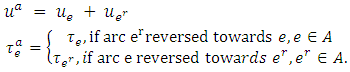 2. On auxiliary network compute generalized flow with capacity
2. On auxiliary network compute generalized flow with capacity 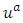 , transit time, and proportional loss factor
, transit time, and proportional loss factor 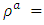
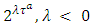 using algorithm of [11] from source to sink.3. Reverse
using algorithm of [11] from source to sink.3. Reverse 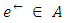 up to the capacity
up to the capacity 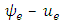 iff
iff 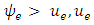 replaced by 0 whenever
replaced by 0 whenever 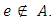 4. For each e ∈ A, if
4. For each e ∈ A, if 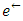 is reversed,
is reversed, 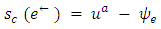 and
and 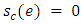 . If neither e nor
. If neither e nor 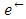 is reversed,
is reversed, 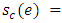
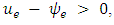 where
where 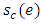 is the saved capacity of e.5. Transform the solution to the original network.To compute the solution of Problem 1, we proceed as follows. First, we convert the given network into an auxiliary network by adding two-way arc capacities. The transit time is asymmetrical and the loss factor is proportional as in [19,27]. So, we take the transit time of the non-reversed arc and loss factor is proportional to transit time of non-reversed arc as defined in Steps 1, 2. On the auxiliary network, we compute maximum generalized flow as in [10,11] and save unused arc capacities. Thus, we obtain the GDPCF solution on the original network with only necessary arc reversals. This process starts with the zero flow, compute a maximum flow in the minimum loss paths, augment this flow, and repeat the process until there is an
is the saved capacity of e.5. Transform the solution to the original network.To compute the solution of Problem 1, we proceed as follows. First, we convert the given network into an auxiliary network by adding two-way arc capacities. The transit time is asymmetrical and the loss factor is proportional as in [19,27]. So, we take the transit time of the non-reversed arc and loss factor is proportional to transit time of non-reversed arc as defined in Steps 1, 2. On the auxiliary network, we compute maximum generalized flow as in [10,11] and save unused arc capacities. Thus, we obtain the GDPCF solution on the original network with only necessary arc reversals. This process starts with the zero flow, compute a maximum flow in the minimum loss paths, augment this flow, and repeat the process until there is an 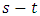 path on the residual network.Theorem 2. The maximum discrete-time GDPCF problem can be computed optimally on
path on the residual network.Theorem 2. The maximum discrete-time GDPCF problem can be computed optimally on 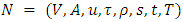 in pseudo-polynomial time complexity.Proof. To prove the theorem, we have to prove the feasibility, optimality, and complexity of the algorithm. Proof of feasibility is obvious as Step 2 of the algorithm is feasible according to [11], and the feasibility of all other steps is shown in [27,20]. After lane reversals, an auxiliary network is formed according to Step 1 of the algorithm. An optimal temporally repeated solution on the auxiliary network is computed, as in [20]. The asymmetric transit time on arcs does not affect the complexity of algorithm. Hence the problem is solved in
in pseudo-polynomial time complexity.Proof. To prove the theorem, we have to prove the feasibility, optimality, and complexity of the algorithm. Proof of feasibility is obvious as Step 2 of the algorithm is feasible according to [11], and the feasibility of all other steps is shown in [27,20]. After lane reversals, an auxiliary network is formed according to Step 1 of the algorithm. An optimal temporally repeated solution on the auxiliary network is computed, as in [20]. The asymmetric transit time on arcs does not affect the complexity of algorithm. Hence the problem is solved in 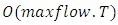 , i.e., pseudo-polynomial time complexity as in [11].Example 1. Consider a single-source single-sink lossy network
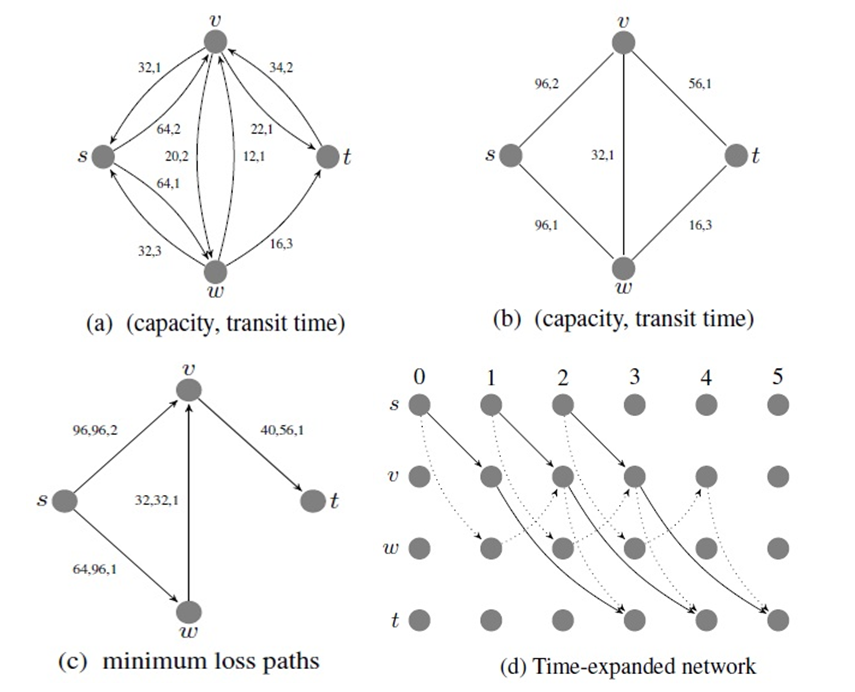
, i.e., pseudo-polynomial time complexity as in [11].Example 1. Consider a single-source single-sink lossy network 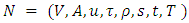 with non-symmetric capacity and transit time on the arcs as shown in Figure 1(a). We calculate the capacity of an arc by adding capacities of anti-parallel arcs and take the transit time of non-reversed arcs according to Step 1 of Algorithm 1 on auxiliary network as shown in Figure 1(b).
with non-symmetric capacity and transit time on the arcs as shown in Figure 1(a). We calculate the capacity of an arc by adding capacities of anti-parallel arcs and take the transit time of non-reversed arcs according to Step 1 of Algorithm 1 on auxiliary network as shown in Figure 1(b).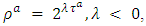 choosing λ = −1 then
choosing λ = −1 then  So, if
So, if 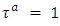 then
then 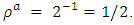 If
If 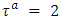 then
then 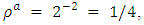 and so on. Since transit time is additive and the loss factor is multiplicative, we can compute the loss factor along the path by multiplying the loss factor of each arc along the path as shown in Tables 1 and 2, respectively.
and so on. Since transit time is additive and the loss factor is multiplicative, we can compute the loss factor along the path by multiplying the loss factor of each arc along the path as shown in Tables 1 and 2, respectively.
|
|
4. Continuous GDPCF on Lossy Network with Asymmetric Transit time
- A natural transformation developed by Fleischer and Tardos [5] transforms discrete-time generalized dynamic flow into continuous-time by the relation
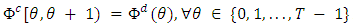 . As discrete dynamic flow satisfies capacity constraints on each arc, continuous dynamic flow does as well. The complexity of continuous-time generalized dynamic flow problem remains unaltered, as these transformations can be per-formed in polynomial-time. Authors in [18,19] presented pseudo-polynomial time algorithm to solve generalized dynamic contraflow problem on the lossy network with asymmetric capacity and symmetric transit time on arcs. In this section, we extend this with asymmetric transit time on arcs and introduce Problem 2.Problem 2. Given a lossy network
. As discrete dynamic flow satisfies capacity constraints on each arc, continuous dynamic flow does as well. The complexity of continuous-time generalized dynamic flow problem remains unaltered, as these transformations can be per-formed in polynomial-time. Authors in [18,19] presented pseudo-polynomial time algorithm to solve generalized dynamic contraflow problem on the lossy network with asymmetric capacity and symmetric transit time on arcs. In this section, we extend this with asymmetric transit time on arcs and introduce Problem 2.Problem 2. Given a lossy network 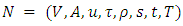 with proportional loss factor on each arc, i.e.,
with proportional loss factor on each arc, i.e., 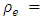
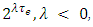 the continuous-time maximum GDPCF problem on a lossy network with asymmetric capacity and transit time on arcs is to obtain the maximum amount of flow that can be sent from
the continuous-time maximum GDPCF problem on a lossy network with asymmetric capacity and transit time on arcs is to obtain the maximum amount of flow that can be sent from 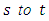 with a minimum loss if the direction of the arc can be reversed at zero processing cost.To solve Problem 1, we modify Algorithm 1 by introducing the relation of natural transformation, and all other steps are the same. As natural transformation transforms the discrete dynamic flow into continuous dynamic flow in polynomial-time, and Algorithm 1 solves Problem 1 optimally. So, the modified algorithm solves Problem 2 optimally, within the same complexity. As a consequence, we state Theorem 3.Theorem 3. The maximum continuous-time GDPCF problem can be computed optimally on
with a minimum loss if the direction of the arc can be reversed at zero processing cost.To solve Problem 1, we modify Algorithm 1 by introducing the relation of natural transformation, and all other steps are the same. As natural transformation transforms the discrete dynamic flow into continuous dynamic flow in polynomial-time, and Algorithm 1 solves Problem 1 optimally. So, the modified algorithm solves Problem 2 optimally, within the same complexity. As a consequence, we state Theorem 3.Theorem 3. The maximum continuous-time GDPCF problem can be computed optimally on 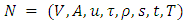 in pseudo-polynomial time complexity.
in pseudo-polynomial time complexity.5. Conclusions
- The natural generalization of the classical maximum flow problem is a generalized maximum flow problem. In classical networks, flow is conserved on each arc. This may not be true in the generalized network due to loss during transmission of flow from one node to another. The generalized static flow problem is polynomial-time solvable, whereas, generalized dynamic flow problem is NP-hard. A lossy network is a network with a gain factor at most one on each arc. By flipping the orientation of necessary arc capacities, the capacity of road segments can be increased, which maximizes the flow value and minimizes the loss. The generalized maximum dynamic contraflow flow on the lossy network with asymmetric capacity and symmetric transit time was solved in pseudo-polynomial time. The partial lane reversal technique increases the flow value and minimizes the loss, as well as save the capacity of unused arcs, that can be used for logistic support in case of an emergency. We introduced GDPCF problems on the lossy network with asymmetric capacity and transit times on arcs in both discrete and continuous-time settings and solved them with pseudo-polynomial time algorithms.
Data Availability
- The authors have not used any additional data in this article.
Conflict of Interest
- The authors declare that they have no conflict of interests regarding the publication of this paper.
ACKNOWLEDGEMENTS
- The first author thanks the University Grants Commission, Nepal, for the Ph.D. research fellowship and second author thanks to the Humboldt Foundation. We also thank the anonymous reviewers for their valuable comments and suggestions to improve the presentation of this paper.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML