-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2020; 10(2): 48-61
doi:10.5923/j.ajcam.20201002.03
Received: Nov. 11, 2020; Accepted: Dec. 3, 2020; Published: Dec. 15, 2020

Nonlinear Dynamics and Active Control in a Liénard-Type Oscillator under Parametric and External Periodic Excitations
Y. J. F. Kpomahou1, J. A. Adéchinan2
1Department of Industrial and Technical Sciences, LARPET, ENSET-Lokossa, UNSTIM-Abomey, Bénin
2Department of Physics, FAST-Natitingou, UNSTIM-Abomey, Benin
Correspondence to: Y. J. F. Kpomahou, Department of Industrial and Technical Sciences, LARPET, ENSET-Lokossa, UNSTIM-Abomey, Bénin.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper, nonlinear dynamics and active control of a Liénard-type oscillator under parametric and external excitations are investigated. The amplitude of the harmonic oscillations and the criteria for the appearance of the Melnikov chaos are derived and analyzed. Analytical predictions are demonstrated through direct numerical simulation. Various bifurcations structures of the system with a single well potential and a double well potential are analyzed. The effects of the control gain parameter on the dynamical behaviour of the forced Liénard-type oscillator are analyzed. As results, it is found that for an appropriate value of the control gain parameter, the chaotic behaviour is completely removed of the system.
Keywords: Forced Liénard-type oscillator, Harmonic dynamics, Melnikov’s chaos, Bifurcations and chaos, Active control
Cite this paper: Y. J. F. Kpomahou, J. A. Adéchinan, Nonlinear Dynamics and Active Control in a Liénard-Type Oscillator under Parametric and External Periodic Excitations, American Journal of Computational and Applied Mathematics , Vol. 10 No. 2, 2020, pp. 48-61. doi: 10.5923/j.ajcam.20201002.03.
Article Outline
1. Introduction
- The Liénard-type equation,
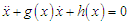 | (1) |
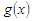 and
and 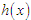 are arbitrary function of
are arbitrary function of 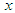 , has been widely used in various fields of science, mathematics, biology and engineering [1-6]. This class of equations contains many dynamical systems exhibiting interesting behaviours. For instance the famous Duffing and Van der Pol oscillators belong to this class of equations. Another interesting nonlinear oscillator belonging to this class of equations is the modified Emden equation defined as follows.
, has been widely used in various fields of science, mathematics, biology and engineering [1-6]. This class of equations contains many dynamical systems exhibiting interesting behaviours. For instance the famous Duffing and Van der Pol oscillators belong to this class of equations. Another interesting nonlinear oscillator belonging to this class of equations is the modified Emden equation defined as follows.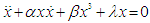 | (2) |
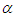 and
and 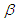 are the nonlinear damping and the strength of nonlinearity respectively.
are the nonlinear damping and the strength of nonlinearity respectively. 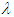 is the natural frequency. Eq. (2) arises in the study of equilibrium configurations of a spherical gas cloud [7]. Chandrasekar et al., [8] showed that for
is the natural frequency. Eq. (2) arises in the study of equilibrium configurations of a spherical gas cloud [7]. Chandrasekar et al., [8] showed that for 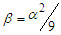 and
and 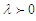 , the amplitude of oscillations of this oscillator does not depend on the frequency This unusual dynamical property exhibited by this oscillator has received attention of many investigators. To that end, various studies have been performed on the different forms of Eq. (2) and interesting results have been obtained [9-14].Generally, forced and damping nonlinear oscillators arise in modeling of many physical and engineering systems such as Josephson junctions, electrical circuits, optical systems, macromechanical and microelectromechanical oscillators, etc [15-19]. Most oscillatory systems are subjected to different damping combinations. Dynamics study of nonlinear damping systems driven by a direct harmonic excitation or parametric excitation have shown that nonlinear damping plays a significant role [20-23]. For instance, it has been shown that nonlinear damping can be used to suppress chaos in oscillatory systems [24-26]. On the other hand, it is important to underline that these oscillatory systems exhibit a rich variety of dynamical behaviour such as: period-doubling bifurcation, symmetry-breaking, intermittency, regular and chaotic behaviours. In this perspective, the Liénard-type equation (2) driven by a direct external periodic forcing or a parametric excitation has been recently studied in the open literature. For instance, Kingston et al., [27] studied the processes of appearance of the extreme events in the forced Liénard system with double well potential. The obtained results have shown that the extreme events occur via two processes, an interior crisis and intermittency. Kaviya et al., [28] also investigated the influence of dissipation on extreme oscillation of a Liénard oscillator with double-well potential. The authors of this paper found that the large-amplitude oscillations developed in this system are completely removed if one incorporates linear damping into the system. On the other hand, Suresh and Chandrasekar [29] studied the appearance of extreme events in Liénard-type and MEMS oscillator under parametric excitation. It has been found that the emergence of extreme events in Liénard-type oscillator occurs via two bifurcation routes, such as intermittency and period-doubling routes for two different critical values of the external frequency. In the parametrically excited microelectromechanical system, the authors showed that the extreme events occur due to the appearance of stick-slip bifurcation near the discontinuous boundary of the system. However the dynamics and active control of a Liénard-type oscillator governed by equation (2) under parametric and external excitations have not been studied in the open literature. Such excitations give rise to complicated and unexpected behaviours of the solutions. Therefore we consider in this paper the following nonlinear oscillator.
, the amplitude of oscillations of this oscillator does not depend on the frequency This unusual dynamical property exhibited by this oscillator has received attention of many investigators. To that end, various studies have been performed on the different forms of Eq. (2) and interesting results have been obtained [9-14].Generally, forced and damping nonlinear oscillators arise in modeling of many physical and engineering systems such as Josephson junctions, electrical circuits, optical systems, macromechanical and microelectromechanical oscillators, etc [15-19]. Most oscillatory systems are subjected to different damping combinations. Dynamics study of nonlinear damping systems driven by a direct harmonic excitation or parametric excitation have shown that nonlinear damping plays a significant role [20-23]. For instance, it has been shown that nonlinear damping can be used to suppress chaos in oscillatory systems [24-26]. On the other hand, it is important to underline that these oscillatory systems exhibit a rich variety of dynamical behaviour such as: period-doubling bifurcation, symmetry-breaking, intermittency, regular and chaotic behaviours. In this perspective, the Liénard-type equation (2) driven by a direct external periodic forcing or a parametric excitation has been recently studied in the open literature. For instance, Kingston et al., [27] studied the processes of appearance of the extreme events in the forced Liénard system with double well potential. The obtained results have shown that the extreme events occur via two processes, an interior crisis and intermittency. Kaviya et al., [28] also investigated the influence of dissipation on extreme oscillation of a Liénard oscillator with double-well potential. The authors of this paper found that the large-amplitude oscillations developed in this system are completely removed if one incorporates linear damping into the system. On the other hand, Suresh and Chandrasekar [29] studied the appearance of extreme events in Liénard-type and MEMS oscillator under parametric excitation. It has been found that the emergence of extreme events in Liénard-type oscillator occurs via two bifurcation routes, such as intermittency and period-doubling routes for two different critical values of the external frequency. In the parametrically excited microelectromechanical system, the authors showed that the extreme events occur due to the appearance of stick-slip bifurcation near the discontinuous boundary of the system. However the dynamics and active control of a Liénard-type oscillator governed by equation (2) under parametric and external excitations have not been studied in the open literature. Such excitations give rise to complicated and unexpected behaviours of the solutions. Therefore we consider in this paper the following nonlinear oscillator.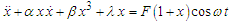 | (3) |
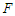 and
and 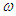 are the amplitude and the frequency of the parametric and external excitations.Since it is well known that the control of regular and irregular motions is an interesting issue in engineering, the behaviour of the model (3) under control may be investigated. For this, an active control is applied and the dynamics of the model are now described by the following set of differential equations
are the amplitude and the frequency of the parametric and external excitations.Since it is well known that the control of regular and irregular motions is an interesting issue in engineering, the behaviour of the model (3) under control may be investigated. For this, an active control is applied and the dynamics of the model are now described by the following set of differential equations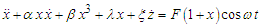 | (4a) |
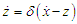 | (4b) |
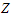 is the control force,
is the control force, 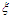 and
and 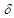 are the parameters of control. In order to study the dynamics and control of such model the following questions deserve to be asked:How does the amplitude
are the parameters of control. In order to study the dynamics and control of such model the following questions deserve to be asked:How does the amplitude 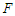 of the parametric and external excitations affects the amplitude of the harmonic oscillations of the Liénard-type system under consideration?Which types of motion occur in the
of the parametric and external excitations affects the amplitude of the harmonic oscillations of the Liénard-type system under consideration?Which types of motion occur in the 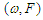 or
or 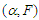 plane with a double-well potential?Which types of bifurcation occur when
plane with a double-well potential?Which types of bifurcation occur when 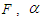 and
and 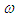 evolve?Which are values of control parameters that lead to a good reduction of the amplitude and a suppression of chaos?In order to answer these questions, we firstly derive the amplitude of the oscillatory states and the criterion of the appearance of chaos in the nonautonomous system using respectively the harmonic balance (section 2) and Melnikov perturbation (section 3) methods. We secondly use numerical simulations to investigate bifurcation mechanisms in the uncontrolled system as the parameters of the system evolve (section 4). Finally, we analyze the effects of the control (section 5) and we end with a conclusion (section 6).
evolve?Which are values of control parameters that lead to a good reduction of the amplitude and a suppression of chaos?In order to answer these questions, we firstly derive the amplitude of the oscillatory states and the criterion of the appearance of chaos in the nonautonomous system using respectively the harmonic balance (section 2) and Melnikov perturbation (section 3) methods. We secondly use numerical simulations to investigate bifurcation mechanisms in the uncontrolled system as the parameters of the system evolve (section 4). Finally, we analyze the effects of the control (section 5) and we end with a conclusion (section 6).2. Forced Oscillatory States
- Our aim is to study the influence of the amplitude of the parametric and external excitations on the amplitude of the harmonic oscillatory state. For this purpose, the harmonic balance method can be used [30,31]. Thus assuming that the fundamental component of the solutions has the period of the external excitation, we express the solution of Eq. (3) as follows.
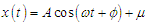 | (5) |
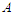 and
and 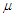 are the amplitude of the oscillations. Injecting the solution
are the amplitude of the oscillations. Injecting the solution 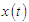 into Eq. (3) and equating the constants and the coefficients of
into Eq. (3) and equating the constants and the coefficients of 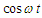 and
and 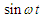 , we obtain after some mathematical operations the following equations:
, we obtain after some mathematical operations the following equations: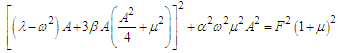 | (6) |
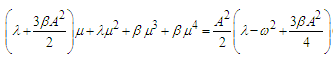 | (7) |
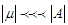 , that is, that shift in
, that is, that shift in  is small compared to the amplitude, then
is small compared to the amplitude, then 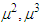 and
and 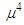 terms in Eq. (7) can be neglected and we obtain
terms in Eq. (7) can be neglected and we obtain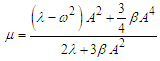 | (8) |
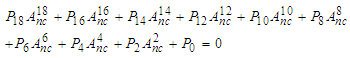 | (9) |
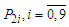 , are given in appendices
, are given in appendices 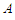 .The comparison between analytical and numerical response frequency curves of the model (3) is shown in Figure 1(a). The behaviour of the amplitude
.The comparison between analytical and numerical response frequency curves of the model (3) is shown in Figure 1(a). The behaviour of the amplitude 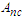 when the amplitude of the parametric and external excitations is varied is illustrated in Figure 1(b) for the case of the single well potential. We clearly see that the amplitude
when the amplitude of the parametric and external excitations is varied is illustrated in Figure 1(b) for the case of the single well potential. We clearly see that the amplitude 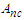 of the harmonic oscillations increases when the amplitude F of the parametric and external excitations increases. The behaviour of the amplitude of the harmonic oscillations when the amplitude of the parametric and external excitations varies is plotted in Figure 2. From Figure 2(a), we notice that in the case of the single-well potential, bifurcation and jump phenomena disappear in the Liénard-type system under consideration when the natural frequency
of the harmonic oscillations increases when the amplitude F of the parametric and external excitations increases. The behaviour of the amplitude of the harmonic oscillations when the amplitude of the parametric and external excitations varies is plotted in Figure 2. From Figure 2(a), we notice that in the case of the single-well potential, bifurcation and jump phenomena disappear in the Liénard-type system under consideration when the natural frequency 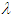 takes the value 1. In the case of the double-well potential (see Figure 2(b)), it appears in the Liénard-type system under study, bifurcation and jump phenomena. Furthermore we also notice the coexistence of small and large-amplitude oscillations.
takes the value 1. In the case of the double-well potential (see Figure 2(b)), it appears in the Liénard-type system under study, bifurcation and jump phenomena. Furthermore we also notice the coexistence of small and large-amplitude oscillations.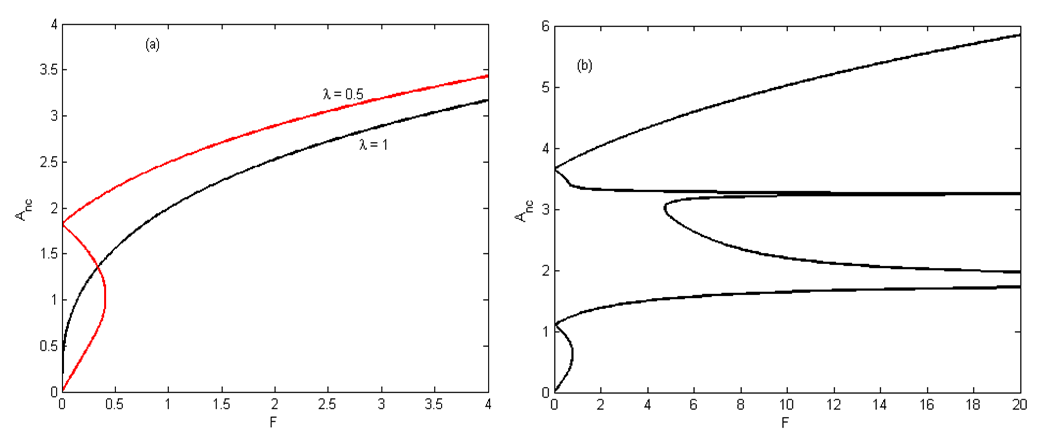 | Figure 2. Analytical frequency-response curves 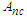 vs vs 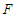 for: (a) for: (a) 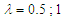 (single-well potential) and (b) (single-well potential) and (b) 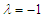 (double-well potential). The other parameters are kept constants (double-well potential). The other parameters are kept constants |
3. Melnikov Chaos
3.1. Melnikov Criterion
- When a nonlinear oscillator is subjected to external excitation, the transition from regular to irregular motion appears. The necessary criterion for appearance of such a transition can be obtained by means of the Melnikov’s theory [32,33]. This theory is today considered as a powerful analytical tool to provide an approximate criterion for the occurrence of hetero/homoclinic chaos in a wide class of dynamical systems. It is widely used by many investigators to detect chaotic dynamics and to analyze near-homoclinic motion with deterministic or random perturbation [34-38]. In this section, we also apply this theory for expressing this criterion in the case of a potential with double well, that is,
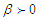 and
and 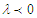 . In this configuration, the system possesses two homoclinic orbits connecting the unstable point
. In this configuration, the system possesses two homoclinic orbits connecting the unstable point 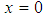 of the potential to itself. These orbits are given by the following components:
of the potential to itself. These orbits are given by the following components: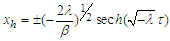 | (10a) |
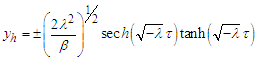 | (10b) |
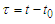 and
and 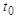 is the cross-section time of the Poincaré map and can be interpreted as the initial time of the forcing time. The Melnikov function is defined by
is the cross-section time of the Poincaré map and can be interpreted as the initial time of the forcing time. The Melnikov function is defined by 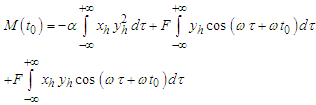 | (11) |
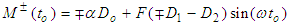 | (12) |
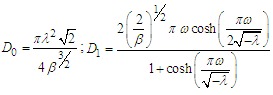 and
and 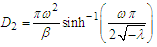 From Eq. (12), we found the following criterion for the Melnikov chaos:
From Eq. (12), we found the following criterion for the Melnikov chaos: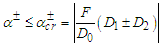 | (13a) |
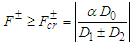 | (13b) |
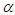 on the frequency
on the frequency 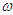 for two different values of the amplitude
for two different values of the amplitude 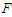 of the parametric and external excitations. From this figure we can conclude that the threshold
of the parametric and external excitations. From this figure we can conclude that the threshold 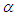 for homoclinic chaos to occur increases when
for homoclinic chaos to occur increases when 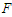 increases. Figure 3(b) also shows the dependence of the amplitude of the parametric and periodic excitations on the frequency
increases. Figure 3(b) also shows the dependence of the amplitude of the parametric and periodic excitations on the frequency 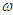 for two different values of
for two different values of 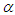 . We notice in this case that the threshold
. We notice in this case that the threshold  decreases as
decreases as  increases.
increases.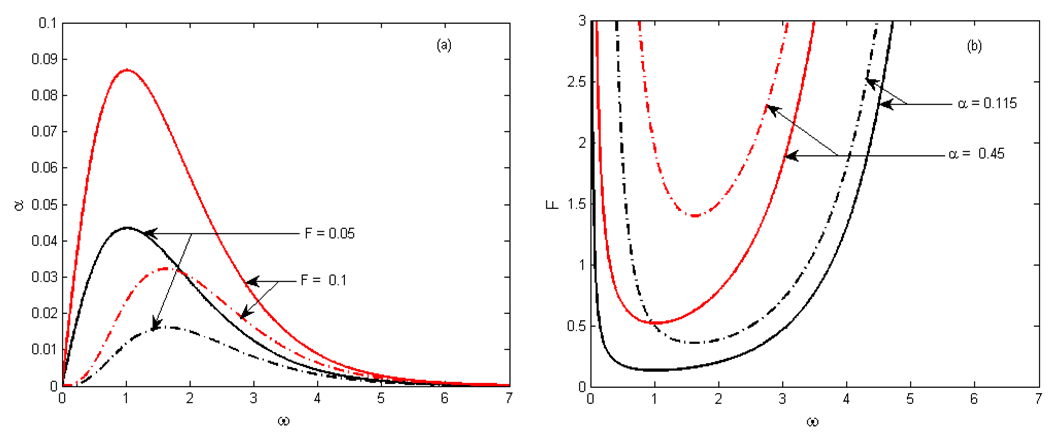 | Figure 3. Melnikov threshold curves ( : solid line and : solid line and 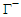 : dashed-lines) for homoclinic chaos to occur in the plane : (a) : dashed-lines) for homoclinic chaos to occur in the plane : (a) 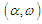 and (b) and (b) 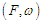 with the parameters with the parameters 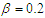 and and 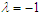 |
3.2. Fractal Basin Boundaries
- The goal of this subsection is to investigate numerically the validity of the analytical predictions obtained in the previous subsection. For this purpose the basins of attraction depicted in Figure 4 is obtained by collecting the initial conditions which attract the dynamics in the either of the wells of the potential for several different values of the amplitude of the external and parametric excitations chosen in the different domains exhibited by Figure 3(b). It is important to point out that in these figures; the blue, red and white regions represent respectively the set of initial conditions around left equilibrium point, right equilibrium point and motion covering both equilibrium points. For
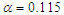 ;
;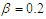 ;
;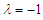 and
and 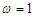 , the Melnikov threshold for the right and left half planes is given analytically by
, the Melnikov threshold for the right and left half planes is given analytically by 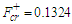 and
and 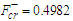 respectively. Thus below these critical values, the system under consideration governed by equation (3) may exhibit a regular behaviour. However chaotic behaviour may appear above these values. For
respectively. Thus below these critical values, the system under consideration governed by equation (3) may exhibit a regular behaviour. However chaotic behaviour may appear above these values. For 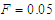 chosen in the regular behaviour domain predicted by the Melnikov criterion, the basin of attraction shows regular solutions (see Figure 4(a)). When the value of the amplitude
chosen in the regular behaviour domain predicted by the Melnikov criterion, the basin of attraction shows regular solutions (see Figure 4(a)). When the value of the amplitude  is chosen in chaotic behaviour region, a fractal structure of the basin of attraction of the initial conditions appears and becomes more and more visible as
is chosen in chaotic behaviour region, a fractal structure of the basin of attraction of the initial conditions appears and becomes more and more visible as  increases (see Figure 4(b)-(e)). We can conclude that the analytical and numerical predictions are in good agreement.
increases (see Figure 4(b)-(e)). We can conclude that the analytical and numerical predictions are in good agreement. 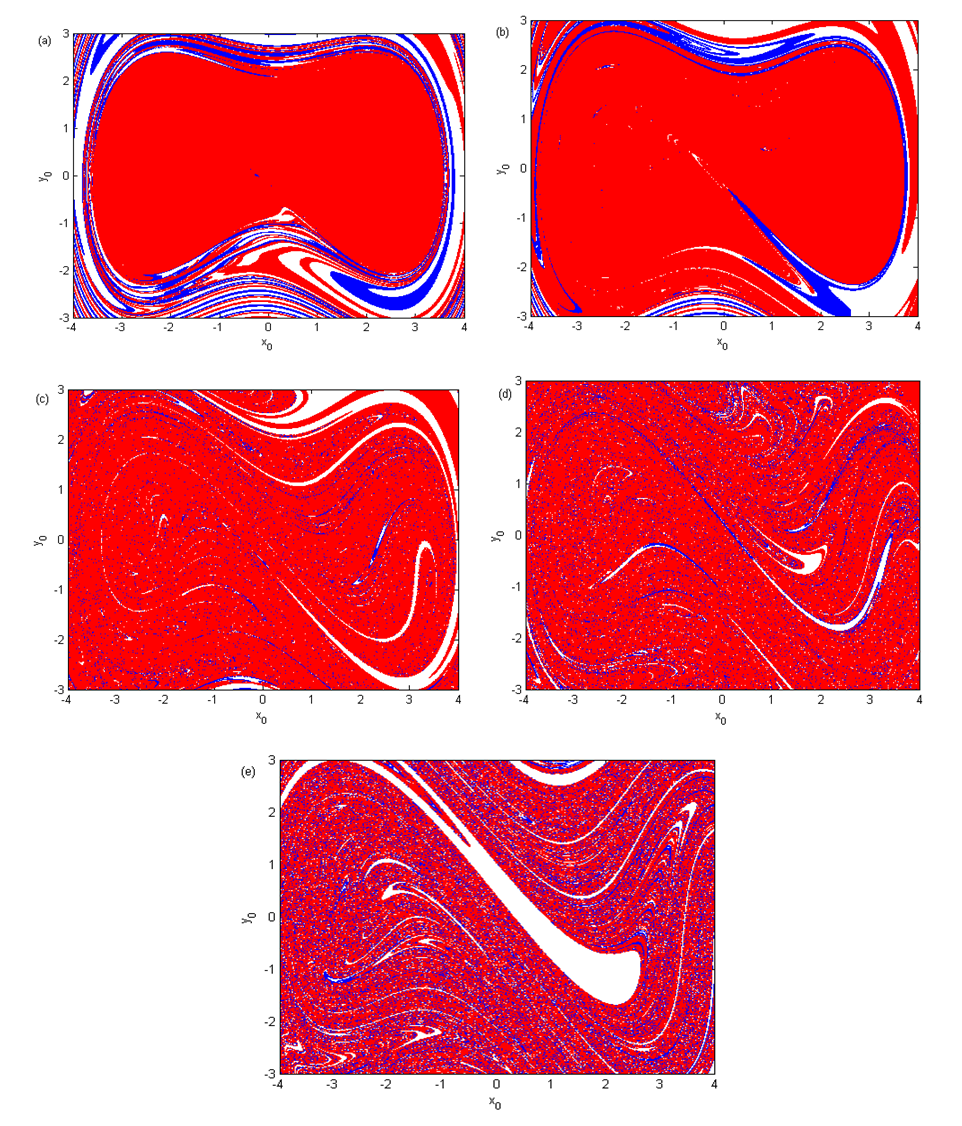 | Figure 4. Basin of attraction of a Liénard-type oscillator in symmetric double well potential case with the parameters: 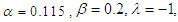 and and 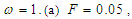 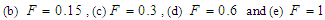 |
4. Bifurcations and Transitions to Chaos
- The aim of this section is to investigate some bifurcation mechanisms in our model when the system parameters as
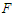 ,
, 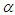 and
and 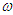 evolve. For this purpose we numerically solve the equation of motion (3) under consideration via the fourth-order Runge-Kutta algorithm. The initial conditions used to perform the numerical simulations are
evolve. For this purpose we numerically solve the equation of motion (3) under consideration via the fourth-order Runge-Kutta algorithm. The initial conditions used to perform the numerical simulations are 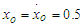 . In the case of the single well potential, when the amplitude of the external and parametric excitations
. In the case of the single well potential, when the amplitude of the external and parametric excitations 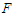 varies, periodic motions exist for
varies, periodic motions exist for 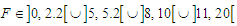 while chaotic motions are obtained for
while chaotic motions are obtained for 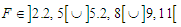 (see Figure 5). We notice that the chaotic dynamics have emerged through two distinct routes such as: period-doubling and intermittency. In order to have an idea on the predictions shown by bifurcation diagram and confirmed by its corresponding Lyapunov exponent, various phase portraits and its Poincaré maps are plotted in Figure 6 for different values of
(see Figure 5). We notice that the chaotic dynamics have emerged through two distinct routes such as: period-doubling and intermittency. In order to have an idea on the predictions shown by bifurcation diagram and confirmed by its corresponding Lyapunov exponent, various phase portraits and its Poincaré maps are plotted in Figure 6 for different values of 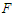 chosen in different attractors regions. In Figure 7 we have examined the influence of the nonlinear damping coefficient,
chosen in different attractors regions. In Figure 7 we have examined the influence of the nonlinear damping coefficient, 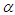 on the bifurcation diagram. From this figure we note that the chaotic domain is reduced as
on the bifurcation diagram. From this figure we note that the chaotic domain is reduced as 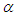 increases. In the case of the double well potential, when
increases. In the case of the double well potential, when 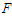 is used as control parameter, the system governed by equation (3) exhibits various bifurcations such as period-one, period doubling, reverse period doubling, period windows, intermittency and chaos (see Figure 8). It is important to point out that our system transits from period one motion to chaotic motion for small values of
is used as control parameter, the system governed by equation (3) exhibits various bifurcations such as period-one, period doubling, reverse period doubling, period windows, intermittency and chaos (see Figure 8). It is important to point out that our system transits from period one motion to chaotic motion for small values of 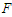 . Moreover, it can vibrate from period-3 motion to chaotic motion. Various phase portraits and its corresponding Poincaré maps of some attractors predicted by bifurcation diagram of Figure 8 are plotted in Figure 9. As
. Moreover, it can vibrate from period-3 motion to chaotic motion. Various phase portraits and its corresponding Poincaré maps of some attractors predicted by bifurcation diagram of Figure 8 are plotted in Figure 9. As 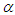 is varied intermittency transition to chaos is only displayed by the system (see Figure 10). On the other hand, when the excitation frequency
is varied intermittency transition to chaos is only displayed by the system (see Figure 10). On the other hand, when the excitation frequency 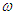 is varied for
is varied for 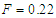 , the Liénard-type oscillator under consideration vibrates from intermittency route to chaotic dynamics (see Figure 11). One can see from this figure that the small-size of the periodic attractor suddenly bifurcates into a large-size chaotic attractor when
, the Liénard-type oscillator under consideration vibrates from intermittency route to chaotic dynamics (see Figure 11). One can see from this figure that the small-size of the periodic attractor suddenly bifurcates into a large-size chaotic attractor when 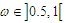 . As
. As 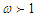 , we clearly see that the large-size chaotic attractor slowly decreases in size and suddenly transforms into a periodic attractor via intermittency bifurcation route.
, we clearly see that the large-size chaotic attractor slowly decreases in size and suddenly transforms into a periodic attractor via intermittency bifurcation route.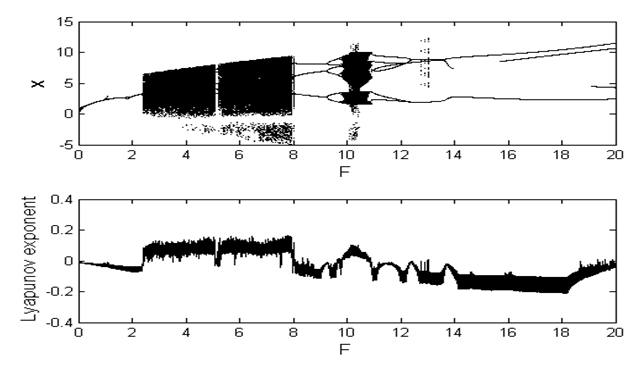 | Figure 5. Bifurcation diagram and corresponding Lyapunov exponent as a function of the amplitude of the external and parametric excitation 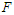 with the parameters with the parameters  and and  |
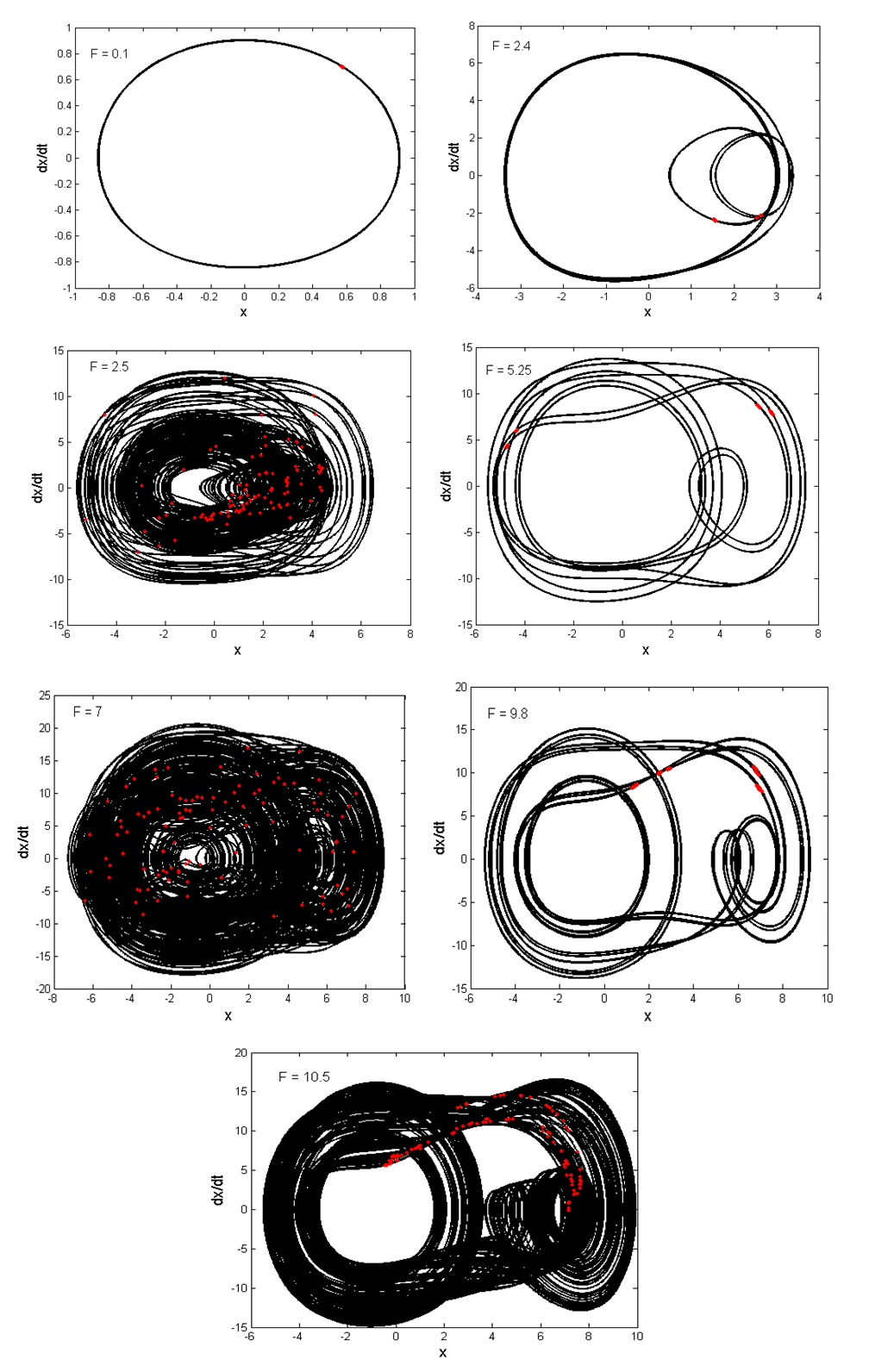 | Figure 6. Various phase portraits and Poincaré maps (in red dot) of a Liénard-type oscillator for several different values of  with the parameters of Figure 5 with the parameters of Figure 5 |
 | Figure 7. Effect of the nonlinear damping coefficient on the Bifurcation diagram of the Liénard-type oscillator with single well potential |
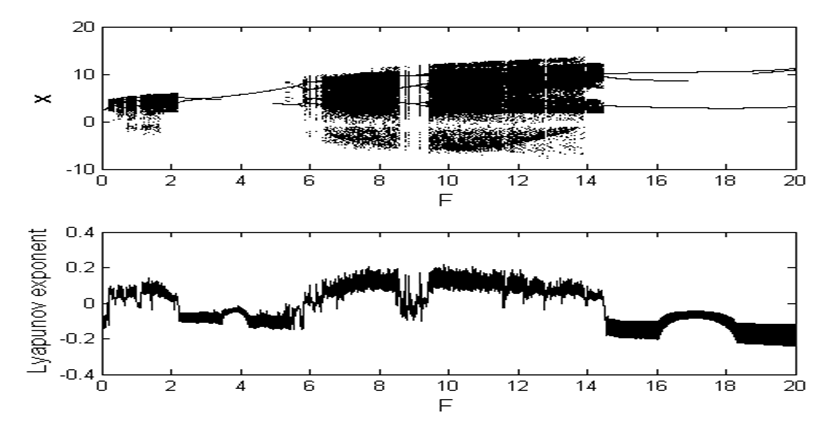 | Figure 8. Bifurcation diagram and corresponding Lyapunov exponent vs the amplitude  with the parameters of Figure 7 for with the parameters of Figure 7 for  (potential with double well) (potential with double well) |
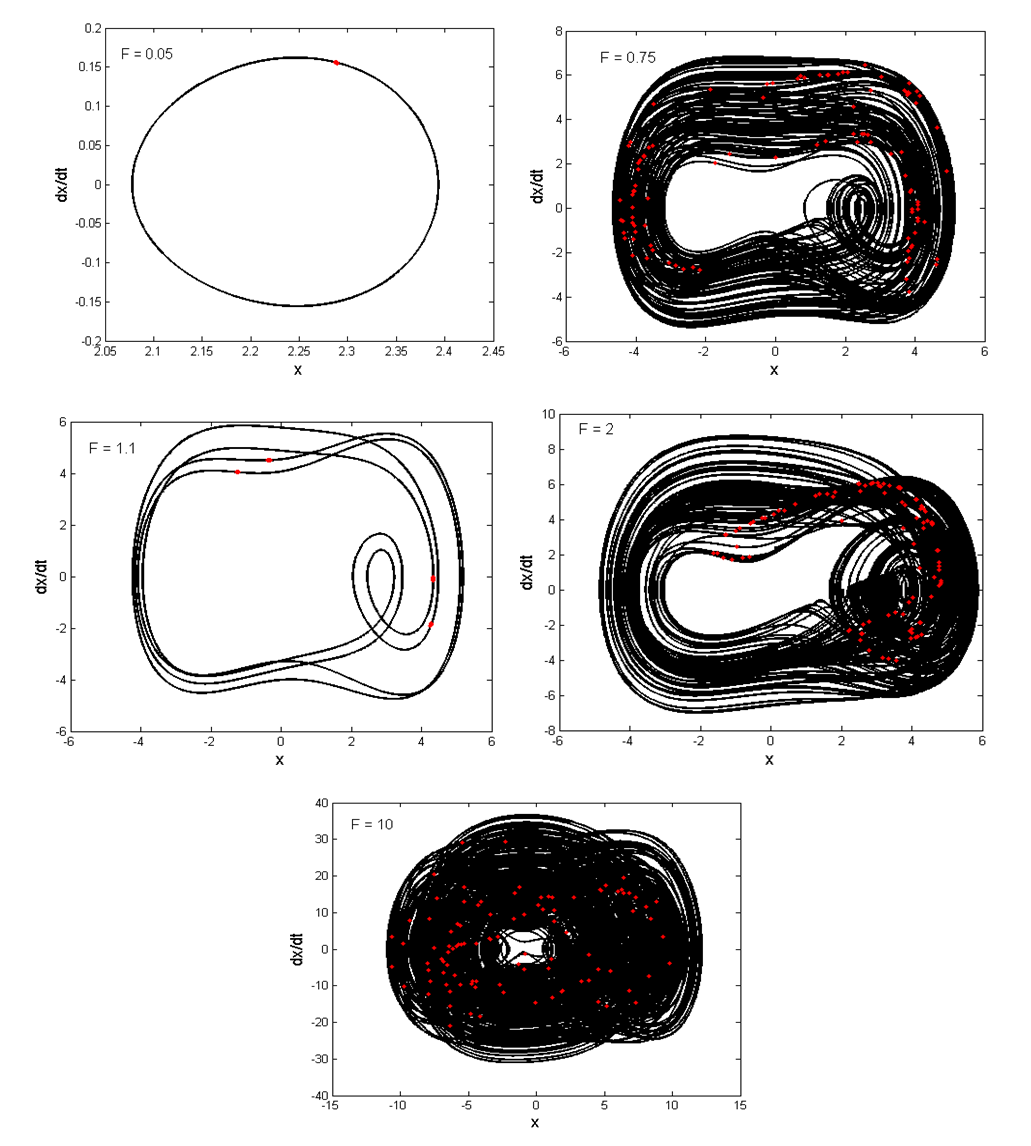 | Figure 9. Various phase portraits and Poincaré maps (in red dot) of a Liénard-type oscillator for several different values of 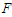 with the parameters of Figure 8 with the parameters of Figure 8 |
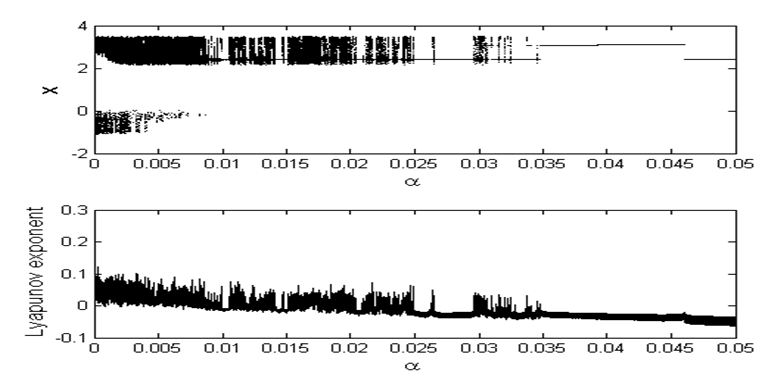 | Figure 10. Bifurcation diagram and corresponding Lyapunov exponent vs 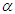 with the parameters of Figure 8 with the parameters of Figure 8 |
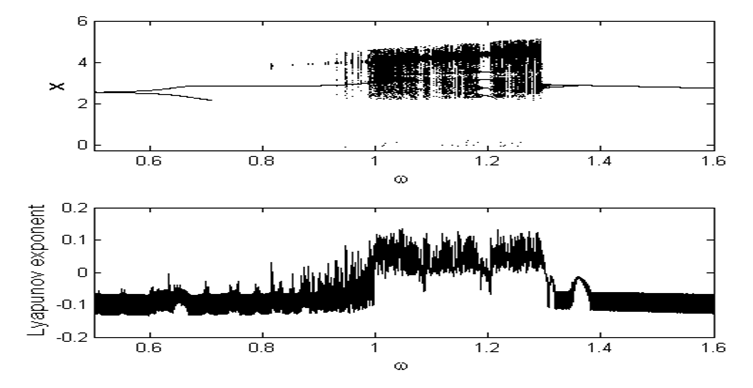 | Figure 11. A Bifurcation diagram and corresponding Lyapunov exponent vs 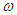 with the parameters of Figure 8 for with the parameters of Figure 8 for 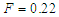 |
5. Active Control
- We have shown in the previous sections that the presence of the parametric and external excitations affects significantly the behaviour of the modified Emden equation. Our goal in this section is to reduce the amplitude of vibration and to suppress the chaotic motion by using the active control. To that end, we investigate in the following subsections the effects of the control on the harmonic vibrations and on the Melnikov chaos. The system under control is governed by the set of differential equations (4a) and (4b).
5.1. Effects of the Control on the Amplitude of Harmonic Oscillations
- In order to determine the amplitude of the vibration of the system under control, we use the method of harmonic balance. Thus, inserting the solution given by Eq. (5) into Eq. (4b), we have
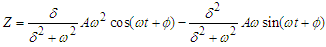 | (14) |
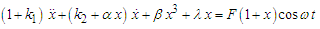 | (15) |
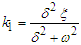 and
and 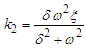 Substituting the solution (5) into Eq. (15) and equating constant, cosine and sine terms separately, we get after some algebraic manipulations the following nonlinear equation:
Substituting the solution (5) into Eq. (15) and equating constant, cosine and sine terms separately, we get after some algebraic manipulations the following nonlinear equation: 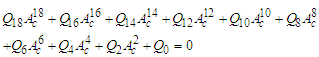 | (16) |
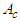 represents the amplitude of the controlled system and the coefficients
represents the amplitude of the controlled system and the coefficients 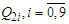 are given in appendices
are given in appendices 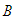 . The amplitude of the oscillations of the controlled system under consideration as a function of the control gain parameter
. The amplitude of the oscillations of the controlled system under consideration as a function of the control gain parameter 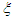 is plotted in Figure 12(left) for the case of the single well potential. The solid horizontal red line represents the amplitude of the oscillations
is plotted in Figure 12(left) for the case of the single well potential. The solid horizontal red line represents the amplitude of the oscillations 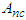 of the uncontrolled system that is
of the uncontrolled system that is 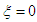 . It is important to point out that the control is effective if and only if
. It is important to point out that the control is effective if and only if  . Thus, we note from this figure that the control is effective if
. Thus, we note from this figure that the control is effective if 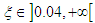 . For the case of the double well potential, the control is only possible for small amplitude oscillation (see Figure 12(right)). This oscillation case shows the coexistence of the small and large-amplitude oscillations.
. For the case of the double well potential, the control is only possible for small amplitude oscillation (see Figure 12(right)). This oscillation case shows the coexistence of the small and large-amplitude oscillations.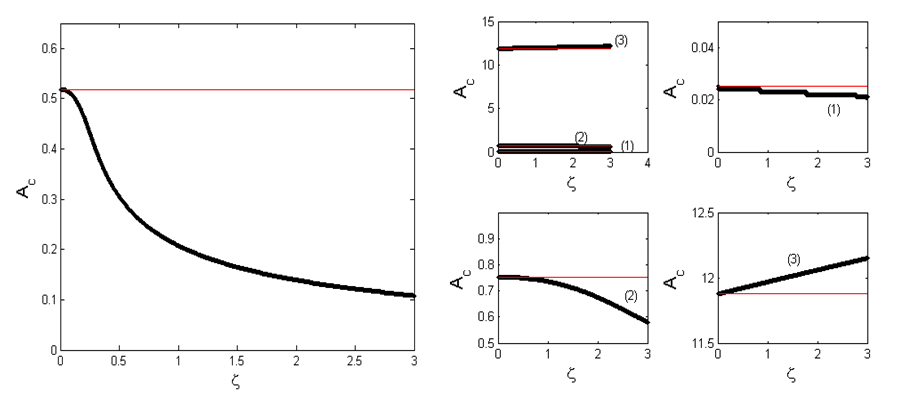 | Figure 12. Effects of the control gain parameter 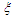 on the amplitude of the Liénard-type oscillator with on the amplitude of the Liénard-type oscillator with 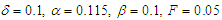 and and 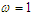 . (left) . (left) 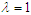 (single well potential) and (right) (single well potential) and (right) 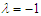 (double well potential) (double well potential) |
5.2. Effects of the Control on the Melnikov Chaos
- We here analyze the effects of the control on the criterion for the appearance of the Melnikov chaos. In order to perform such an analysis we seek the separatrices of the controlled system and the corresponding Melnikov function. Thus for a double-well potential, the homoclinic orbits are defined by (10a) and (10b) and the corresponding controlled component is given by
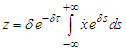 | (17) |
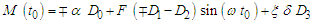 | (18) |
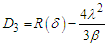 with
with 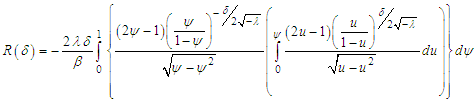 The necessary condition for the appearance of the Melnikov chaos is given by:
The necessary condition for the appearance of the Melnikov chaos is given by: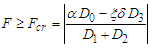 | (19) |
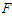 for homoclinic chaos to occur for the uncontrolled system increases when
for homoclinic chaos to occur for the uncontrolled system increases when 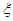 increases. In order to verify this analytical prediction, the basin of attraction of the controlled system under consideration is plotted in Figure 14 with different values of the control gain parameter
increases. In order to verify this analytical prediction, the basin of attraction of the controlled system under consideration is plotted in Figure 14 with different values of the control gain parameter 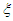 . The others parameters used to realize this simulation are:
. The others parameters used to realize this simulation are: 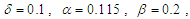
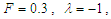 and
and 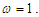 From this figure we conclude that the fractal behaviour of the basin of attraction effectively disappears when
From this figure we conclude that the fractal behaviour of the basin of attraction effectively disappears when 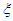 increases.
increases.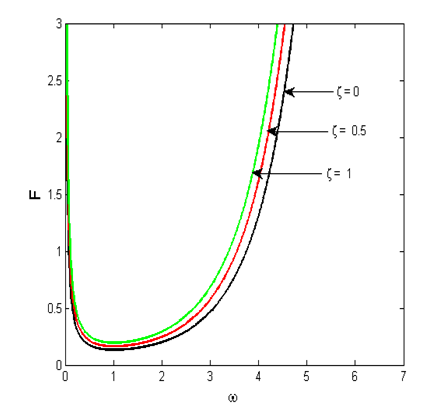 | Figure 13. Effects of the control gain 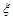 on the Melnikov threshold of the uncontrolled system. The others parameters are: on the Melnikov threshold of the uncontrolled system. The others parameters are: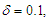 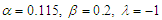 and and 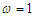 |
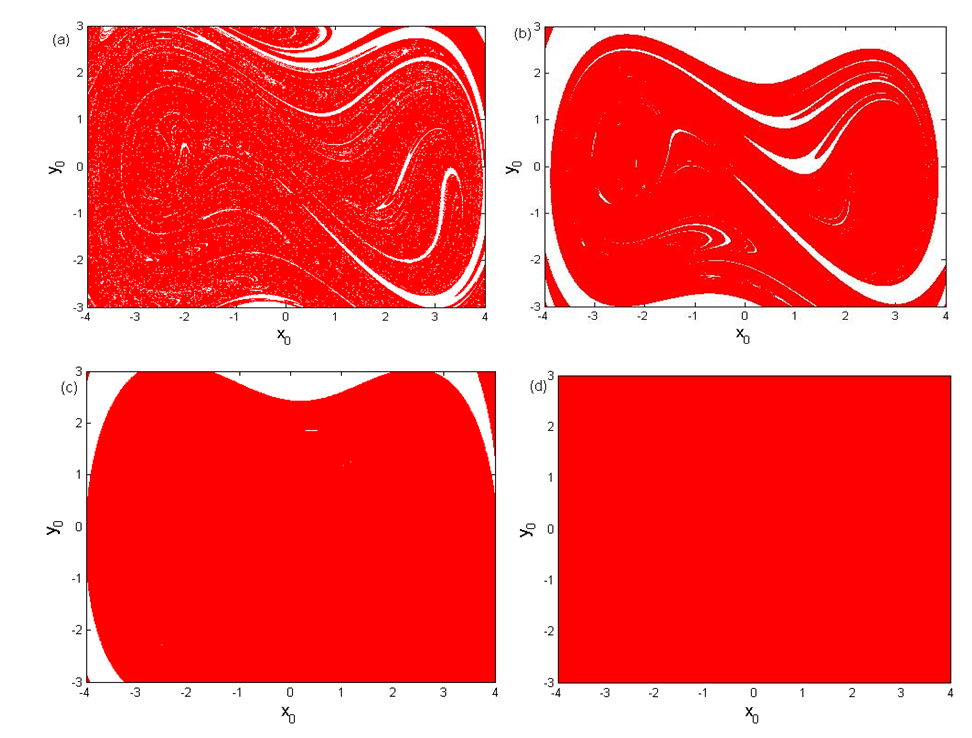 | Figure 14. Effects of the control gain 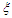 on the basin of attraction: on the basin of attraction: 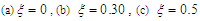 and and 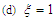 |
5.3. Quenching of Chaotic Motions
- We have shown analytically and numerically in the previous sections that the Liénard-type system under study displays periodic and chaotic motions in the case of a single-well and double-well potential. The goal of this subsection is to investigate numerically the control gain value that can lead to a total suppression of chaos in the model under consideration. For this purpose we use numerical simulations to find various bifurcation structures of the controlled system (4) as the amplitude of the parametric and external excitations
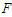 evolves. Thus, in the case of the single-well potential, we clearly see from Figure 15(a) that the chaos completely disappears in our system for
evolves. Thus, in the case of the single-well potential, we clearly see from Figure 15(a) that the chaos completely disappears in our system for 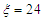 . For
. For 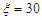 the chaotic behaviour is completely removed in the Liénard-type oscillator with double-well potential under consideration (see Figure 15(b)).
the chaotic behaviour is completely removed in the Liénard-type oscillator with double-well potential under consideration (see Figure 15(b)).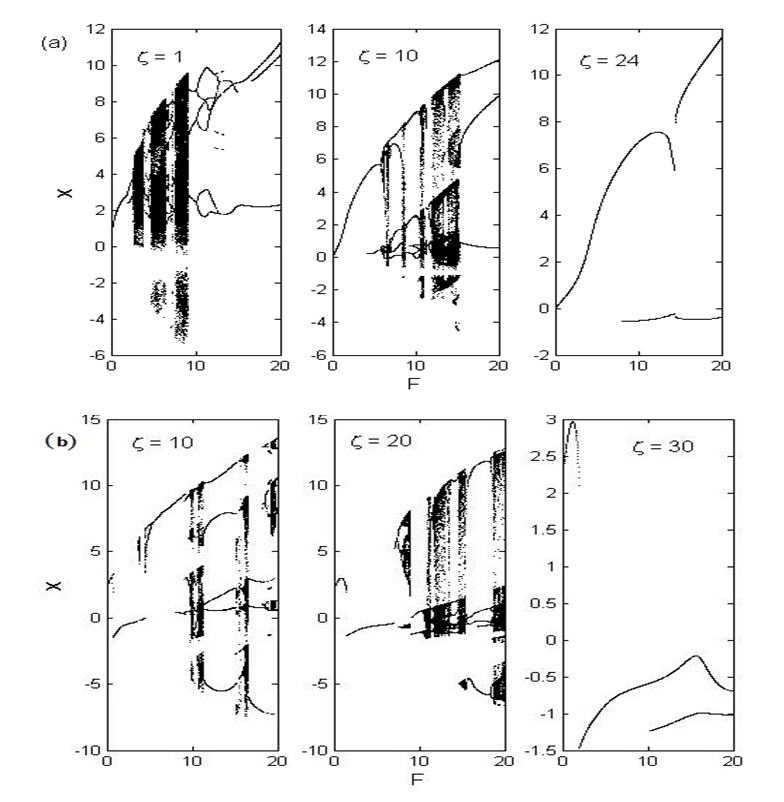 | Figure 15. Suppression of chaos in the Liénard-type oscillator with: (a) 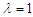 (single-well potential) and (b) (single-well potential) and (b) 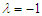 (double-well potential). The other parameters are: (double-well potential). The other parameters are: 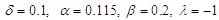 and and 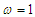 |
6. Conclusions
- Nonlinear dynamics and active control of a forced Liénard-type oscillator have been studied in this paper. The harmonic balance method and the Melnikov perturbation method have been used to derive the amplitude of the harmonic oscillations and the criteria for the appearance of the horseshoe chaos, respectively. The analytical and direct numerical simulations are in good agreement. Various bifurcation mechanisms of our system when
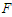 ,
, 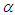 and
and  evolve are analyzed. The effects of the control gain parameter on the behaviour of the system are analyzed and the obtained results have shown that for an appropriate value of the control gain parameter, the quenching of the chaotic behaviour occurs.
evolve are analyzed. The effects of the control gain parameter on the behaviour of the system are analyzed and the obtained results have shown that for an appropriate value of the control gain parameter, the quenching of the chaotic behaviour occurs.Appendices A
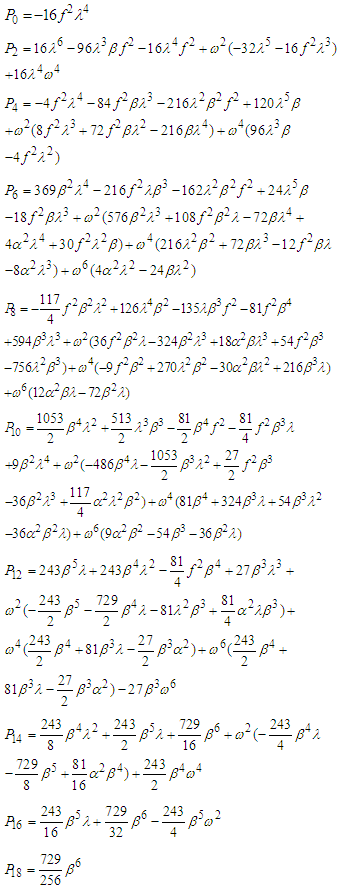
Appendices B
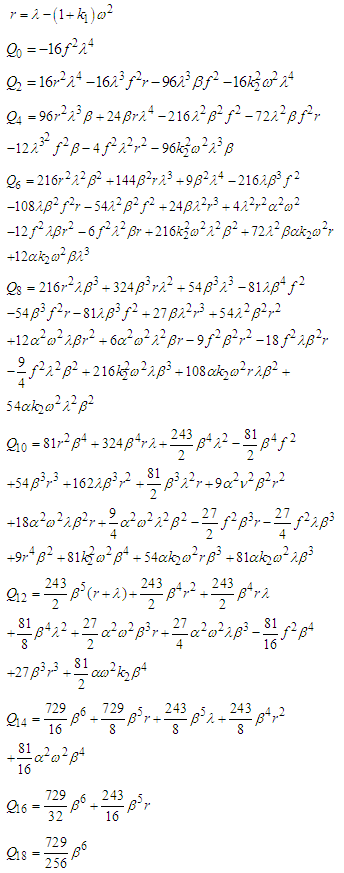
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML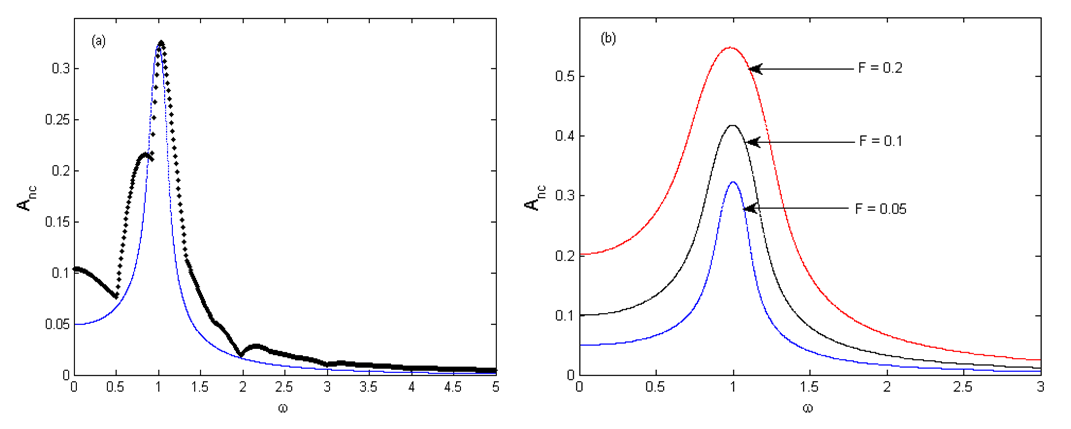
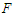 on the amplitude of the harmonic oscillatory states for the case of the single-well potential with the parameters
on the amplitude of the harmonic oscillatory states for the case of the single-well potential with the parameters 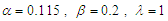 and
and 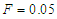
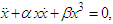 J. Phys. A: Math. Theor. 40(4717).
J. Phys. A: Math. Theor. 40(4717).