Mečislovas Mariūnas
Department of Biomechanical Engineering, Vilnius Gediminas Technical University, Vilnius LT, Lithuania
Correspondence to: Mečislovas Mariūnas, Department of Biomechanical Engineering, Vilnius Gediminas Technical University, Vilnius LT, Lithuania.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
This paper presents methods for determining resonant and parametric excitation frequencies in a nonlinear two-degree-of-freedom dynamic system. It is clarified that in order to determine the resonant frequencies in the system, it must be divided into two subsystems. The results show that in nonlinear dynamic system there are nine groups of resonant frequencies, which are defined by energy, force, stiffness connection peculiarities, as well as the total stiffness of the system. The results also demonstrate that the system for determining the parametric frequencies must not be divided into subsystems. It is clarified that the system generated a very wide spectrum of parametric excitation frequencies, and when they coincide with the resonant frequency, the level of system vibrations increases significantly. It has been found that vibrations at high amplitude resonant frequency also become generators of parametric vibrations in a nonlinear dynamic system. By setting the parameters of the system (stiffness, mass, damping, etc.), we determine its resonant frequencies; however, the magnitude of the parametric vibration frequency and their number of a dynamic system depend on the level of nonlinearity of the system. Thus, the frequency of parametric vibration is independent of their amplitude. The certainty of the analytical methods presented in the paper was verified by numerical calculations.
Keywords:
Methods for determination of resonant and parametric frequencies, Nonlinear two degree of freedom, Dynamic system, Quadratic, Cubic and fourth order nonlinearities, Vibration
Cite this paper: Mečislovas Mariūnas, Methods for Determining Resonant and Parametric Excitation Frequencies of Nonlinear Two Degree of Freedom Dynamic Systems, American Journal of Computational and Applied Mathematics , Vol. 10 No. 2, 2020, pp. 39-47. doi: 10.5923/j.ajcam.20201002.02.
1. Introduction
In order to create a nonlinear mechanical dynamic system and ensure its sustained and stable operation, safe working conditions need to be determined. This can be achieved at the design stage by establishing the resonant frequencies of nonlinear vibration, and also the proper operating modes of the system. Resonance is a known concept in linear system analysis and its study is important in many branches of engineering. At a particular resonance the frequency of an exciting force matches the natural frequency of the system, with the result that energy transmission is efficient and the amplitude of vibration becomes significant. In this paper, the example of two degree of freedom coupled oscillator with quadratic, cubic and fourth order nonlinearities stiffness is considered. This system is representative of a range of applications in structural dynamics, see [1- 12]. For example, in [7-8] the method of multiple scales perturbation technique used to analyze the response of this system. Four ordinary differential equations are derived to describe the modulation of the amplitudes and phases of the two modes of vibrations for the principal parametric resonances. The steady-state solutions and their stability are determined and representative numerical results are included. The theoretical resonance cases of this system have been obtained from the first approximation differential equations and some of them are confirmed by applying well-known numerical techniques. The stability of the obtained numerical solution is studied using phase–plane method. The effect of different parameters on the magnitude of vibration of this system are investigated [6]. In this study, the authors provide an analytical method for relating the backbone curves, found using the second-order normal form technique, to the forced responses. This is achieved using an energy-based analysis to predict the resonant crossing points between the forced responses and the backbone curves. Additionally, a method for assessing the accuracy of the prediction of the resonant crossing points is then introduced, and these predictions are then compared to responses found using numerical continuation.In paper [12], the vibration of a typical two degree of freedom nonlinear system with repeated linearized natural frequencies was investigated systematically. The method of multiple scales is used to obtain the amplitude- phase portraits by introducing the energy ratios and phase differences. It is found that the normal in-unison modal motions, elliptic out-of-unison modal motions are analogous to the polarization of classical optic theory. Furthermore, some kinds of periodic and chaotic motions under out-of-unison and in-unison excitations are investigated numerically. The result of that study offers a detailed discussion of nonlinear modal motions and responses of two degree of freedom systems with cubic nonlinear terms.In paper [11] the amplitude frequency characteristic equation of the system, based on the multi-harmonic method, was derived and the corresponding curve of the relationship between the amplitude and frequency is given. The influence of the current on the curve is researched. Results showed a presence of two pseudo-resonant peaks in the amplitude–frequency curve: one peak- in the low frequency range, the other exists in higher frequency range.In [3-4,6-8] approximate methods and numerical research have also been applied to investigate nonlinear dynamical systems. However, the resonant frequencies of the nonlinear two degree of freedom system determined in this way are not accurate enough, an analysis of the literature suggests there is no exact method for determining the system’s resonant frequencies. In short, the approximate methods used do not explain the physics of vibration of nonlinear dynamical systems. Moreover, they do not show the specificity of their behavior compared to linear systems. The resonant and parametric frequencies in nonlinear one degree of freedom dynamic system were analyzed in [5]. That paper presents methods for determining resonant and parametric excitation frequencies in a nonlinear single-degree-of-freedom dynamic system. It was found that in nonlinear dynamic system there are four groups of resonant frequencies, which are defined by energy, force, stiffness connection peculiarities, as well as the total stiffness of the system. The results also demonstrate that the system generates a very wide spectrum of parametric excitation frequencies. However, research has been done on a dynamic system with one degree of freedom. Thus, the purpose of this research was to study the physics of vibration of nonlinear two-degree-of-freedom dynamic systems, to explain their features, to provide methods for determining the resonant and parametric excitation frequencies of the system, to clarify the frequencies of internal excitation, generated through the properties of the nonlinear dynamic system itself, and to show their destructive effects on the vibration level of the system.
2. Resonant Frequency of the System
The nonlinear of two degree of freedom dynamical system (Figure 1) is described by the following system of differential equations: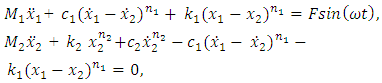 | (1) |
where 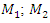 are masses of the system;
are masses of the system; 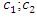 are coefficients of damping;
are coefficients of damping; 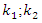 are coefficients of stiffness;
are coefficients of stiffness; 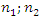 are exponents of
are exponents of 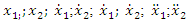 are velocities and accelerations; F is amplitude of external excitement force;
are velocities and accelerations; F is amplitude of external excitement force; 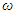 is angular frequency; t is time.
is angular frequency; t is time. 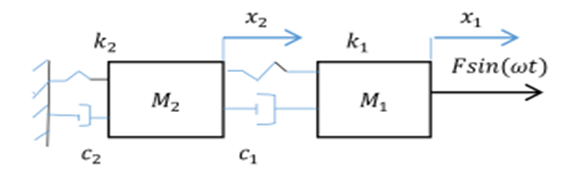 | Figure 1. Two degree of freedom vibration system for linear motion |
By studying a nonlinear dynamic system with one degree of freedom, it was found that its resonant frequencies do not depend on the frequency of excitation forces [5]. Therefore, for determining the resonant frequencies of the nonlinear two degree of freedom dynamic system (1), it can be divided into two subsystems: one with mass 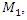 spring
spring 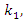 damping coefficient
damping coefficient 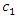 and external excitation force
and external excitation force 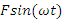 , and the other - with mass
, and the other - with mass 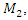 spring
spring  and the damping coefficient
and the damping coefficient 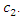 Thus, the system of equations (1) is rearranged as follows:
Thus, the system of equations (1) is rearranged as follows: 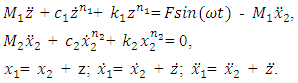 | (2) |
In the system of equations (2) we have two nonlinear dynamical systems of the one degree of freedom. Therefore, to determine the resonant frequencies in each of them, we will apply the method examined in [5], based on the fact that when x = 1 (because 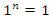 ), the nonlinear dynamic system becomes linear:
), the nonlinear dynamic system becomes linear: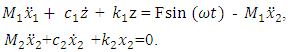 | (3) |
when 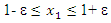 and
and 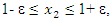 where ε magnitude is small enough.Evaluating the existing peculiarities of the force, stiffness and energy connection in a nonlinear dynamic system, using the method developed in [5], a system of three homogeneous equations is formed for the first subsystem:
where ε magnitude is small enough.Evaluating the existing peculiarities of the force, stiffness and energy connection in a nonlinear dynamic system, using the method developed in [5], a system of three homogeneous equations is formed for the first subsystem: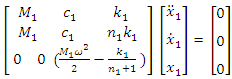 | (4) |
When 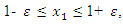 where
where 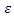 magnitude is small enough.The first row of the matrix (4) evaluates the effects of the force, the second – the effects of the stiffness and the third - of the energy connection peculiarities in a nonlinear dynamic system. From the system of homogeneous equations (4) it is determined that:
magnitude is small enough.The first row of the matrix (4) evaluates the effects of the force, the second – the effects of the stiffness and the third - of the energy connection peculiarities in a nonlinear dynamic system. From the system of homogeneous equations (4) it is determined that: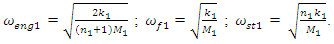 | (5) |
It can be seen from the dependences of (5) that in a nonlinear dynamic system, when the value of the 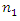 parameter increases, the frequency generated by the energy connection peculiarities decreases and the frequency generated by the stiffness connection peculiarities increases. Meanwhile, the frequency generated by the force connection peculiarities does not depend on the value of the
parameter increases, the frequency generated by the energy connection peculiarities decreases and the frequency generated by the stiffness connection peculiarities increases. Meanwhile, the frequency generated by the force connection peculiarities does not depend on the value of the 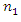 parameter.When
parameter.When 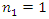 , then from the resonant frequency dependencies (5) of the considered subsystems we get that:
, then from the resonant frequency dependencies (5) of the considered subsystems we get that: 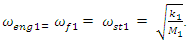 | (6) |
The result of dependence (6) shows that in the present case there will be only one resonant frequency in the latter subsystem. The dynamic system under consideration contains springs, defined by the peculiarities of the coupling of energy, force and stiffness, which are sequentially connected to each other. Therefore, it will also have the whole stiffness of the subsystem, the magnitude of which will be assessed as follows: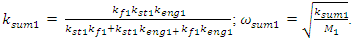 | (7) |
A common case 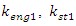 and
and 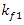 values are calculated according to expressions:
values are calculated according to expressions: 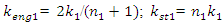 and
and 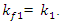 A system of linear homogeneous equations for the second subsystem is formed analogously:
A system of linear homogeneous equations for the second subsystem is formed analogously: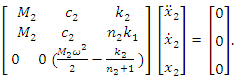 | (8) |
From the system of homogeneous equations (8) it is determined that: 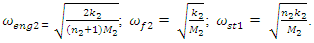 | (9) |
Then the total stiffness and angular frequency of the second subsystem will be evaluated as follows: 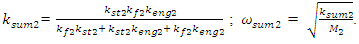 | (10) |
The total stiffness and angular frequency of the whole system will be evaluated as follows: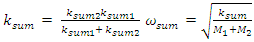 | (11) |
Thus, the nonlinear dynamic system under discussion will have nine resonant frequencies: 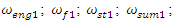
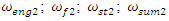 and
and 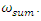 If the exponents of
If the exponents of 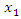 and
and 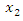 are equal
are equal 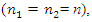 then the number of resonant frequencies in the system (1) will not change, but some values will change, because a multiplier n is used instead of
then the number of resonant frequencies in the system (1) will not change, but some values will change, because a multiplier n is used instead of 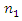 and
and 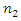 in equations (4) and (8).
in equations (4) and (8).
3. Parametric Excitation Frequency of the System
In order to investigate the resonant and parametric frequencies of the system and verify the obtained analytical results, the Runge – Kutta methods of numerical analysis was performed. Systems with quadratic, cubic and fourth order nonlinearities were examined. The resonant frequencies of the system with the quadratic nonlinearity, whose system parameters are: 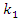 = 100000 N/m;
= 100000 N/m; 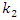 = 40000 N/m; F = 100000 N;
= 40000 N/m; F = 100000 N; 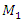 = 5.0 kg;
= 5.0 kg; 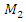 = 3.0 kg;
= 3.0 kg; 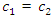 = 0.05, were calculated using formulas (5), (7-11). The following results were obtained:
= 0.05, were calculated using formulas (5), (7-11). The following results were obtained: 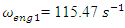 ;
; 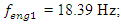
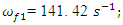
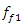 = 22.52 Hz;
= 22.52 Hz; 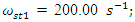
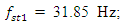
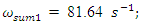
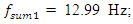
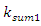 = 33325.12 N/m;
= 33325.12 N/m; 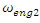 = 94.28
= 94.28  = 15.01 Hz;
= 15.01 Hz; 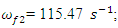
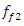 = 18.38 Hz;
= 18.38 Hz; 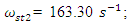
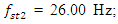
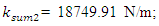
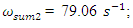
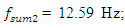
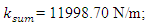
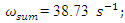
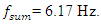 Analyzing the search graphs shown in Figure 2 and 4, we will notice when the system is excited at the frequency
Analyzing the search graphs shown in Figure 2 and 4, we will notice when the system is excited at the frequency 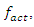 then the spectral density contains only a part of the calculation at the system resonant frequency. The other part of the resonant frequencies is covered by vibrations of higher intensity of the system. It should be noted that when
then the spectral density contains only a part of the calculation at the system resonant frequency. The other part of the resonant frequencies is covered by vibrations of higher intensity of the system. It should be noted that when 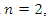 the system excites sufficiently large vibration amplitudes at a frequency of
the system excites sufficiently large vibration amplitudes at a frequency of 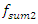 = 12.59 Hz (Figure 2), although it is exited at frequency
= 12.59 Hz (Figure 2), although it is exited at frequency 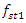 = 31.85 Hz. The magnitudes of the latter vibrations in time are modulated by frequency subharmonic
= 31.85 Hz. The magnitudes of the latter vibrations in time are modulated by frequency subharmonic 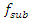 = 3.08 Hz of resonant frequency
= 3.08 Hz of resonant frequency 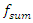 = 6.0 Hz. And this can be seen very clearly in the graphs provided in Figure 2. However, such vibrations in a nonlinear dynamic system occur only at the beginning, and after a few seconds they mainly vibrate at the excitation frequency. It is important to note that the analysis of nonlinear dynamic system initial vibrations allows to see the frequencies of the system subsystems and subharmonic frequencies. When a nonlinear dynamic system is excited by
= 6.0 Hz. And this can be seen very clearly in the graphs provided in Figure 2. However, such vibrations in a nonlinear dynamic system occur only at the beginning, and after a few seconds they mainly vibrate at the excitation frequency. It is important to note that the analysis of nonlinear dynamic system initial vibrations allows to see the frequencies of the system subsystems and subharmonic frequencies. When a nonlinear dynamic system is excited by 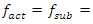 3.08 Hz, it generates high amplitude vibrations at the resonant frequency
3.08 Hz, it generates high amplitude vibrations at the resonant frequency 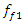 = 22.52 Hz (Figure 4) and it is modulated at a frequency of
= 22.52 Hz (Figure 4) and it is modulated at a frequency of 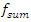 = 6.17 Hz, whereas
= 6.17 Hz, whereas 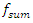 is 4 times repeated the system resonant
is 4 times repeated the system resonant 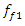 frequency. The subharmonic frequency
frequency. The subharmonic frequency 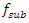 is approximately 7 times repeated and for the resonant frequency
is approximately 7 times repeated and for the resonant frequency 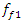 = 22.52 Hz as well, but the vibration intensity of the latter frequency is lower so it is practically not seen in the vibration graph of Figure 4. Therefore, the choice of operating modes and parameters of the system should not allow it to operate under resonant conditions.
= 22.52 Hz as well, but the vibration intensity of the latter frequency is lower so it is practically not seen in the vibration graph of Figure 4. Therefore, the choice of operating modes and parameters of the system should not allow it to operate under resonant conditions.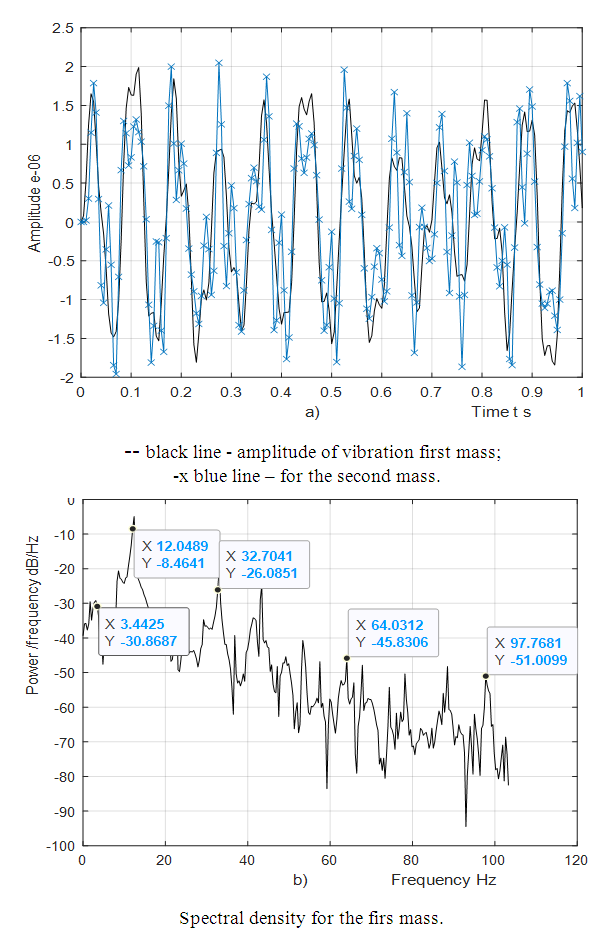 | Figure 2. Result of solution of vibration and spectral density for the quadratic nonlinearity when 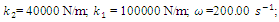 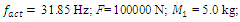 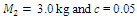 |
The spectral density plots in Figure 2-4 contain many non-resonant system frequencies. In order to determine their nature, it is necessary to examine the frequencies of parametric vibration generated by the nonlinear dynamic system. In the paper [5] examining a nonlinear dynamic system of one degree of freedom, it was found that the frequencies of parametric vibrations depend on the frequency of excitation forces, the magnitude of the nonlinearity parameters of the system, but did not depend on mass, spring stiffness, vibration amplitude, and other parameters. Therefore, in order to determine the parametric vibration frequencies of the system, it does not have to be divided into subsystems. In this case, the total effect of all forces on the excitation frequencies of the parametric vibration must be examined. It can be seen from (1) that the first equation of the system contains four forces: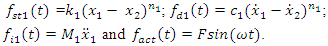 | (12) |
The second equation of the system (1) has five forces: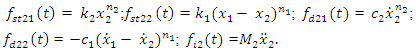 | (13) |
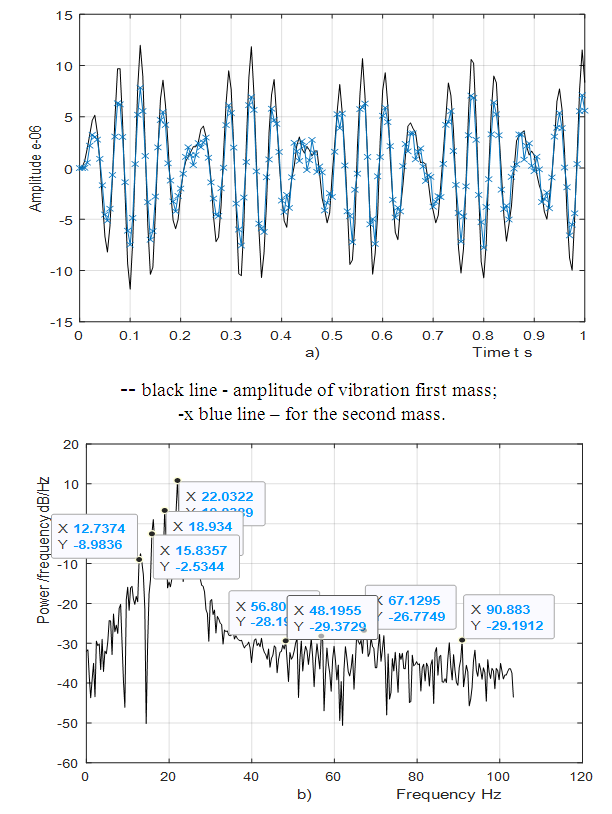 | Figure 3. Result of solution of vibration and spectral density for the quadratic nonlinearity when 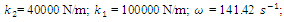 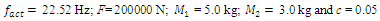 |
To determine parametric vibration frequencies, let us consider the changes of the velocity and acceleration of stiffness, damping and inertia forces of nonlinear dynamic system (1) under the influence of the external excitation force. Let’s say the aforementioned force 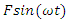 will excite vibrations
will excite vibrations 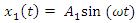 and
and 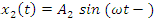 in the nonlinear two degree of freedom system. The dynamic system under consideration contains 9 different types of forces (12) and (13).In the first step, we will consider the frequencies of parametric vibration in the system (12) generated by stiffness, damping, inertia and external excitation forces. When
in the nonlinear two degree of freedom system. The dynamic system under consideration contains 9 different types of forces (12) and (13).In the first step, we will consider the frequencies of parametric vibration in the system (12) generated by stiffness, damping, inertia and external excitation forces. When 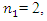 the force
the force 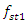 will be expressed as follows:
will be expressed as follows: 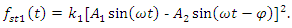 | (14) |
Then we will determine the total velocity of the forces 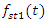 and
and 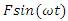 as follows:
as follows: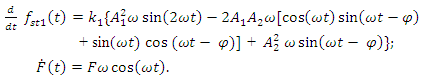 | (15) |
By setting the velocity expression (15) to the expression 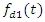 (12) we get the expression of damping force:
(12) we get the expression of damping force: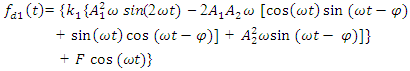 | (16) |
By setting the second derivative of the expression (16) to the expression 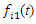 (12) we get the force of inertia, which excites the frequencies of parametric vibrations of the system:
(12) we get the force of inertia, which excites the frequencies of parametric vibrations of the system: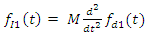 | (17) |
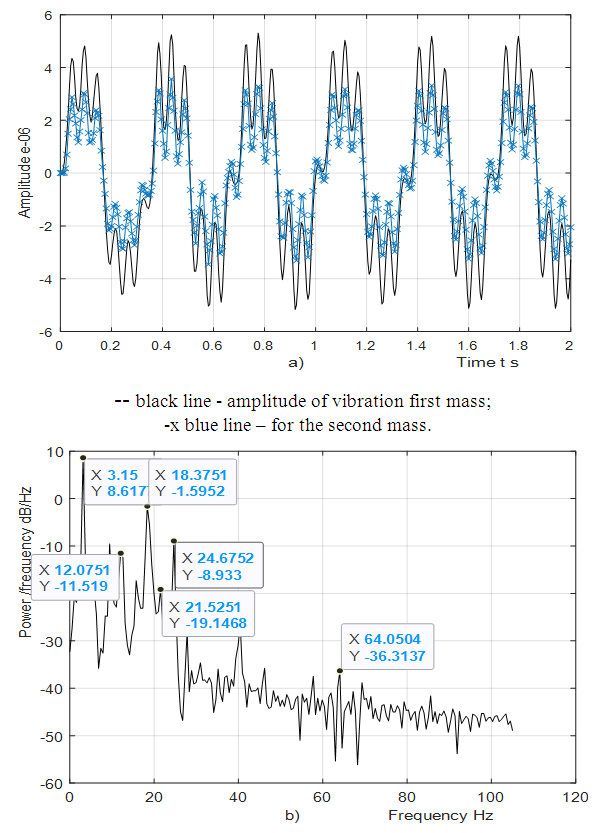 | Figure 4. Result of solution of vibration and spectral density for the quadratic nonlinearity when 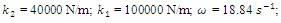 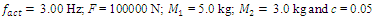 |
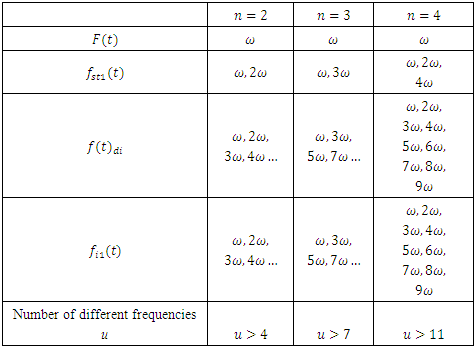
Similarly, velocities and accelerations of other forces at n > 2 can be found. Because the expressions of the velocities and accelerations are complicated, we do not discuss them further in this paper. Analyzing the expressions of force, velocity and acceleration (14-17) we find that when n = 2, the vibrating system will generate parametric frequencies: stiffness force  damping force
damping force 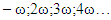 The frequencies generated by the forces under consideration are shown in Table 1 below.In this way, when n = 2, the system will generate parametric vibration with frequency:
The frequencies generated by the forces under consideration are shown in Table 1 below.In this way, when n = 2, the system will generate parametric vibration with frequency: 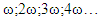 or the frequencies of parametric vibration generated in the system can be described as follows:
or the frequencies of parametric vibration generated in the system can be described as follows: 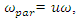 when u = 1;2;3;4… By performing analogous steps we will determine the frequencies of parametric vibrations generated in the second subsystem and when
when u = 1;2;3;4… By performing analogous steps we will determine the frequencies of parametric vibrations generated in the second subsystem and when 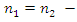 parametric vibration of the same frequencies generated in the second subsystem.
parametric vibration of the same frequencies generated in the second subsystem. 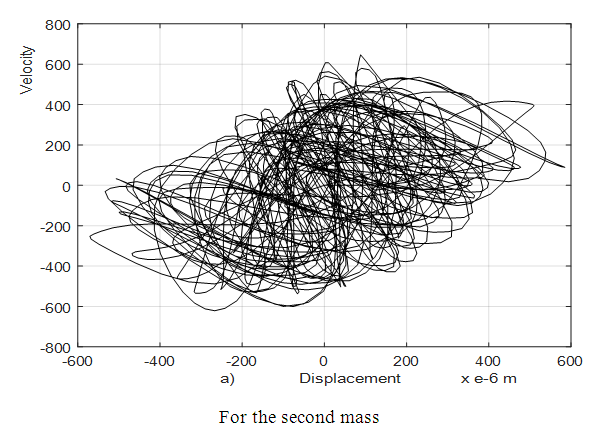 | Figure 5. Result of solution of the phase – space diagram for the quadratic nonlinearity when 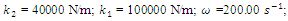 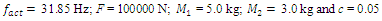 |
Another table of velocity and acceleration frequencies for the second subsystem can be created in an analogous way. But it would only repeat the contents of the Table 1.Table 1. The frequencies of velocity and accelerations of the forces acting on the system
 |
| |
|
When 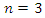 then we will write the expression of stiffness force as follows:
then we will write the expression of stiffness force as follows: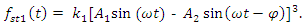 | (18) |
When 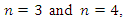 then the expressions of the velocities and accelerations of force changes become long and uninformative, therefore they expressions are not presented in this paper.However, graphs of their regularity of change are shown in Figure 6a and b.
then the expressions of the velocities and accelerations of force changes become long and uninformative, therefore they expressions are not presented in this paper.However, graphs of their regularity of change are shown in Figure 6a and b. 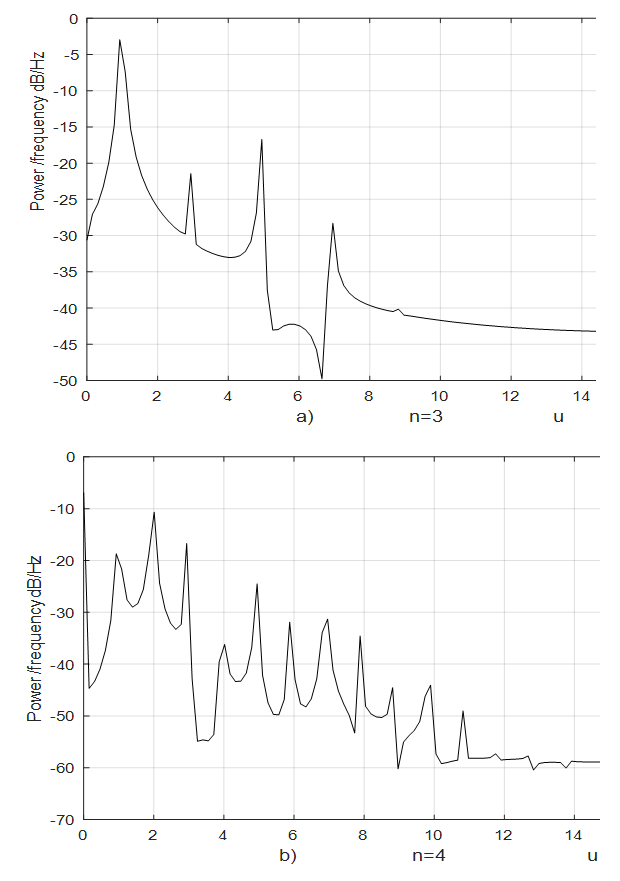 | Figure 6. Spectral density for the damping force, when 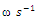 |
Examining Table 1 and the results of the above study, it was found that when 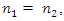 the exponents of the variables of
the exponents of the variables of 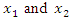 and their combinations determine the regularity of the change of the parameter u and its dependence can be expressed as follows:
and their combinations determine the regularity of the change of the parameter u and its dependence can be expressed as follows: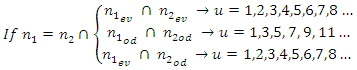 | (19) |
where 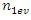 and
and 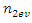 are even numbers;
are even numbers; 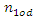 and
and 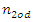 - odd numbers;
- odd numbers; 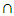 is conjunction;
is conjunction; 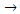 is implication.Then in the general case we will determine the frequencies of parametric vibration in a nonlinear system of two degrees of freedom as follows:
is implication.Then in the general case we will determine the frequencies of parametric vibration in a nonlinear system of two degrees of freedom as follows: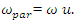 | (20) |
Where the values of the parameter u are determined by the dependence (19) The equations (14 - 18) show only a fraction of the frequencies generated by velocity and acceleration forces in a nonlinear dynamic system. All frequencies generated by a nonlinear dynamic system are described in a conditionally called table (21). The analysis of the dependencies (13-18), as well as the data in Table 1 and Figure 2-4 shows that:To determine the resonant frequencies of a nonlinear dynamic system of two degrees of freedom, it is necessary to divide it into subsystems and form systems of three equations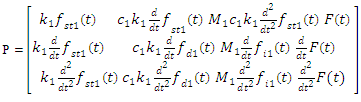 | (21) |
for each of them, the solutions of which would be the latter frequencies;To determine the frequencies of parametric vibrations, the system must not be divided into subsystems, because the total effect of all forces on it must be evaluated;• When n >1, a dynamic system generates parametric vibrations of additional frequencies and the higher the value of the parameter n the more of them will be generated; • In the dynamical system, as the values of the parametric frequencies increase, the amplitudes of the vibrations decrease significantly (Figure 6);• Results of the study showed that the frequency of parametric vibrations is independent of their amplitude. Their number and magnitude depend on the parameters of the nonlinearity of the dynamic system;• Generated parametric vibration frequencies in nonlinear dynamical subsystems, can be estimated (evaluated) by the members of first row of the matrix–table P.Thus, these study demonstrate that the two degree of freedom nonlinear dynamic system (1) has resonant and parametric vibration frequencies, and identifies analytical ways to determine them.
4. Numerical Analysis and Discussion
When the nonlinear dynamic system vibrates, all resonant frequencies will get in it, although the magnitude of their vibrations will not be the same (Figure 2a and b and Figure 4a and b). Hence, the level of vibrations will be higher for those resonant frequencies where the frequency of external excitation force will be repeated. Analyzing the data in Figure 2, we will observe that in a nonlinear dynamic system, high-amplitude vibrations also generate parametric vibrations and their intensity may be higher than vibrations exited by external forces. For example, the frequencies of parametric vibrations generated by external excitation forces vary: 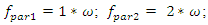
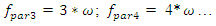 And the high-amplitude vibration of the frequency also generate parametric vibrations (Figure 1), but at different frequencies:
And the high-amplitude vibration of the frequency also generate parametric vibrations (Figure 1), but at different frequencies: 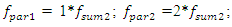
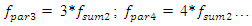 However, the resonant frequency
However, the resonant frequency 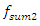 = 12.01 Hz (Figure 1b) generates parametric vibrations of significantly higher amplitude as compared to the vibrations excited by the external force. The results in Figure 3 show that the frequency
= 12.01 Hz (Figure 1b) generates parametric vibrations of significantly higher amplitude as compared to the vibrations excited by the external force. The results in Figure 3 show that the frequency 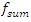 = 6.17 Hz significantly modulates the vibration when the nonlinear system excites at a frequency
= 6.17 Hz significantly modulates the vibration when the nonlinear system excites at a frequency 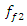 = 22.7 Hz, which corresponds to the frequency excited by the force connection peculiarities. Meanwhile, choosing the appropriate frequency of excitation force can significantly reduce vibration modulation and avoid nonlinear dynamic system pulsating vibration, for example, in the case discussed in Figure 2. In the example examined earlier, there is still an undesirable thing, such as
= 22.7 Hz, which corresponds to the frequency excited by the force connection peculiarities. Meanwhile, choosing the appropriate frequency of excitation force can significantly reduce vibration modulation and avoid nonlinear dynamic system pulsating vibration, for example, in the case discussed in Figure 2. In the example examined earlier, there is still an undesirable thing, such as 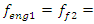 18.38 Hz. In addition, the system total frequency
18.38 Hz. In addition, the system total frequency 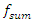 = 6.17 Hz is 5 times repeated the external excitation force frequency and three times repeated the
= 6.17 Hz is 5 times repeated the external excitation force frequency and three times repeated the 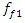 = 22.52 Hz frequency. Thus, by properly selecting the dynamic system parameters and the external excitation force frequency, the system vibration levels could be reduced. In this way, parametric vibration frequencies are generated not only by external excitation force, but also by high-amplitude vibrations of a nonlinear dynamic system. It is therefore necessary to emphasize that the vibrations generated by external forces may not always be greatest. If high amplitudes of vibration are excited in the system by other parametric frequencies, then the vibrations of the latter parametric frequencies will predominate in it, and the external excitation forces generated by the parametric vibration can almost be invisible. For the system with cubic nonlinearity whose parameters are:
= 22.52 Hz frequency. Thus, by properly selecting the dynamic system parameters and the external excitation force frequency, the system vibration levels could be reduced. In this way, parametric vibration frequencies are generated not only by external excitation force, but also by high-amplitude vibrations of a nonlinear dynamic system. It is therefore necessary to emphasize that the vibrations generated by external forces may not always be greatest. If high amplitudes of vibration are excited in the system by other parametric frequencies, then the vibrations of the latter parametric frequencies will predominate in it, and the external excitation forces generated by the parametric vibration can almost be invisible. For the system with cubic nonlinearity whose parameters are: 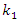 = 100000 N/m;
= 100000 N/m; 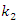 = 40000 N/m; F = 100000 N;
= 40000 N/m; F = 100000 N; 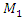 = 5.0 kg;
= 5.0 kg; 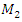 = 3.0 kg;
= 3.0 kg; 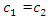 = 0.05, the resonant frequencies of the system were calculated using the formulas (5), (7), (9), (10), (11). The following results were obtained:
= 0.05, the resonant frequencies of the system were calculated using the formulas (5), (7), (9), (10), (11). The following results were obtained: 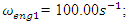
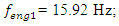
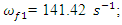
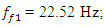
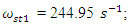
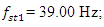
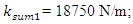
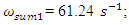
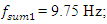
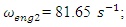
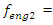
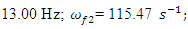
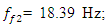
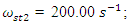
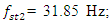
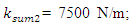
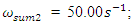
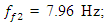
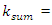
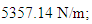
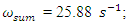
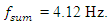 The spectra of vibrations of masses
The spectra of vibrations of masses 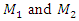 are shown in Figures 7a and b. The results of the study show that the frequency of parametric vibrations in the system changes according to the analytically determined dependence (20). Dynamic system with cubic nonlinearity is more robust than quadratic nonlinearity systems and extremely high vibration modulation at some frequencies is not observed.The spectrum of masses
are shown in Figures 7a and b. The results of the study show that the frequency of parametric vibrations in the system changes according to the analytically determined dependence (20). Dynamic system with cubic nonlinearity is more robust than quadratic nonlinearity systems and extremely high vibration modulation at some frequencies is not observed.The spectrum of masses 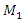 (Figure 7b) shows a small peak at a very low frequency
(Figure 7b) shows a small peak at a very low frequency 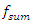 = 4.69 Hz, which is the vibration frequency generated by the total stiffness of the system.
= 4.69 Hz, which is the vibration frequency generated by the total stiffness of the system. 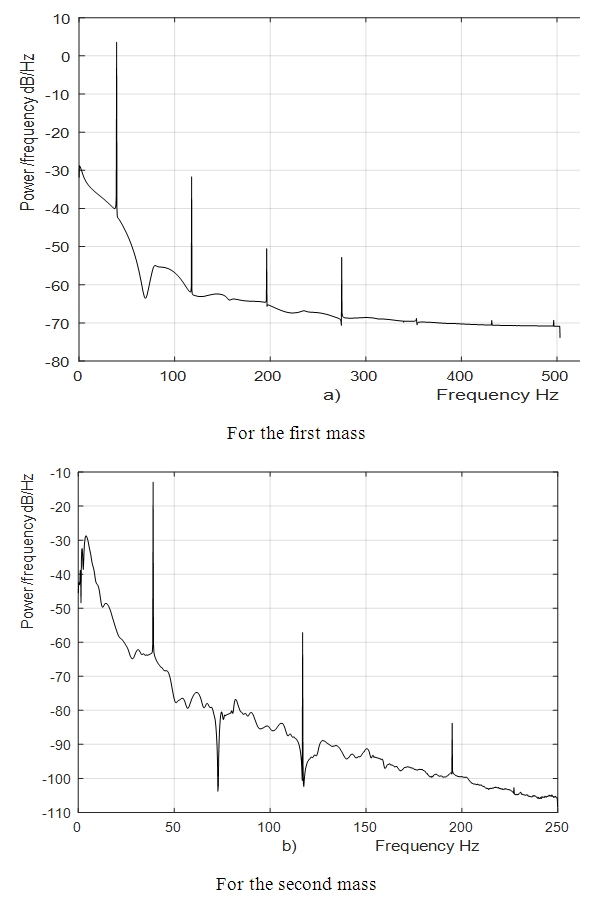 | Figure 7. Result of solution of vibration and spectral density for the cubic nonlinearity when 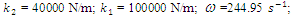 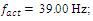 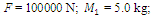 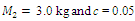 |
The phase – space diagrams of masses  are shown in Figure 8. When n = 2, then the phase – space diagrams are very uninformative, therefore they are not presented in this paper.
are shown in Figure 8. When n = 2, then the phase – space diagrams are very uninformative, therefore they are not presented in this paper. | Figure 8. Result of solution of the phase – space diagram for the cubic nonlinearity when 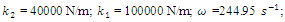 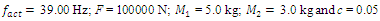 |
For the dynamic system with fourth order nonlinearity whose parameters are: 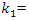 100000 N/m;
100000 N/m; 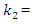 40000 N/m; F = 100000 N;
40000 N/m; F = 100000 N; 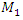 = 5.0 kg;
= 5.0 kg; 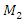 = 3.0 kg;
= 3.0 kg; 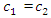 = 0.05, a system frequency which evaluate the stiffness connection peculiarities in a nonlinear dynamic system was determined:
= 0.05, a system frequency which evaluate the stiffness connection peculiarities in a nonlinear dynamic system was determined: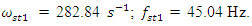 The spectrum of the second mass vibrations for the latter frequency is shown in Figure 9. It can be seen that the spectral density contains all frequencies of parametric vibration as determined analytically, and secondly, for even numbers of the parameter u the spectral intensity is much lower. An analogous vibration spectrum was determined for the first mass of the system as well.
The spectrum of the second mass vibrations for the latter frequency is shown in Figure 9. It can be seen that the spectral density contains all frequencies of parametric vibration as determined analytically, and secondly, for even numbers of the parameter u the spectral intensity is much lower. An analogous vibration spectrum was determined for the first mass of the system as well.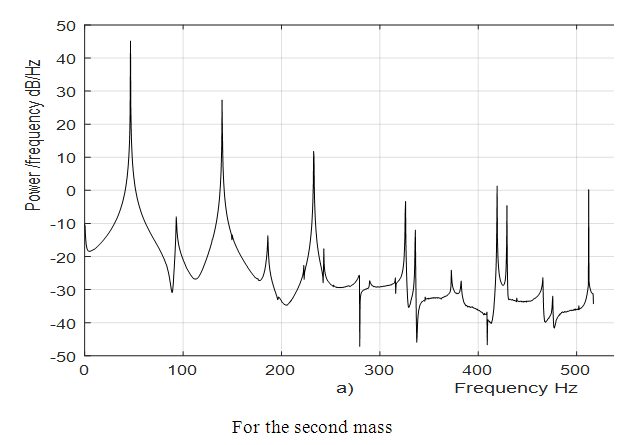 | Figure 9. Spectral density for the fourth order nonlinearity when 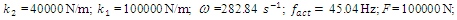 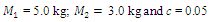 |
Thus, without determining resonant and parametric frequencies in a vibrating nonlinear dynamic system, we will not be able to explain the complexity of the process of vibrations and we will not be able to determine properly the dynamic parameters and operating modes of the system. So, the results of the study show that is very important to determine the appropriate parameters and operating modes of the system at the design process. Notwithstanding [1-16], no such results have been reported, and neither has there been any analytical determination of nonlinear dynamic relationships between resonant and parametric frequencies and its external excitation frequency. Moreover, scientific works [1-12] do not reveal: force, stiffness and energy relations in the vibrating nonlinear dynamical system and their influence on resonant frequencies. In this way, it was impossible to explain the physics of the processes taking place in the vibration nonlinear dynamic system, to create a nonlinear mechanical dynamic system and to determine its safe working conditions, which ensure its lasting and stable operation. The numerical investigation showed that the presented methods for determining the resonant and parametric excitation frequencies are correct and can be used in the design process for calculating their values for quadratic, cubic and fourth order nonlinearities of the two-degree-of-freedom system.
5. Conclusions
This paper presents analytical methods for determining the resonant and parametric excitation frequencies of the systems, which enable choosing reasonable dynamic characteristics of the system during the design process for quadratic, cubic and fourth order nonlinearities of two-degree-of-freedom nonlinear dynamic systems (1) and to reduce its vibration level.Analytical results The analytical results indicate that:1. To determine the resonant frequencies of a nonlinear dynamic system of two degrees of freedom, it is necessary to divide it into two subsystems. There will be four groups of resonant frequencies in each, determined by the energy, force and stiffness characteristic connections peculiarities and the total stiffness of the nonlinear dynamical subsystems. 2. To determine the frequencies of the parametric vibrations of the system, the system cannot be subdivided into subsystems. The frequencies of the latter vibration are determined by estimating the total effect of all forces on a nonlinear dynamic system of two degrees of freedom. 3. The nonlinear dynamic system generates a very wide spectrum of parametric excitation frequencies and the higher the value of the n parameter the more of them will be generated. The frequency of parametric vibration is independent of their amplitude. Parametric excitation frequencies are u times repetitive by the frequency of acting forces in the system.4. When the exponent of polynomial increase then the frequencies determined by the energy characteristic connection peculiarities decrease, while frequencies determined by stiffness connections peculiarities increase.5. The system's resonant frequencies, which are determined by the force connection peculiarities, are not dependent on the exponent of polynomial. The results of numerical calculationsThe results of numerical calculations allow us to prove that:1. It was found that parametric vibration frequencies are generated not only by external excitation force, but also by high-amplitude oscillations of a nonlinear dynamic system. Therefore, the choice of operating modes and parameters of the system should not allow it to operate under resonant conditions; 2. The vibration level of the system significantly increases when the parametric excitation frequency coincides with the system's resonant frequency.3. In the dynamical system, as the values of the parametric frequencies increase, the amplitudes of the vibration decrease significantly.4. By setting the system’s parameters (stiffness, mass, damping, etc.), we determine its resonant frequencies, but the frequency of parametric vibrations and number of them of a dynamic system depend on the level of nonlinearity of the system.5. The certainty of the analytical methods was verified by numerical calculations.
References
| [1] | Wagg D.J., Virgin L., 2012, Exploiting Nonlinear Behavior in Structural Dynamics, Springer, Vienna, pp. 53-109. CrossRefView Record in ScopusGoogle Scholar. |
| [2] | Neild S.A., Wagg D.J., 2013, A generalized frequency detuning method for multidegree-of-freedom oscillators with nonlinear stiffness. Nonlinear Dynamics, 73, pp. 649-663, 10.1007/s11071-013-0818-7. CrossRefView Record in ScopusGoogle Scholar. |
| [3] | Cammarano A., Hill T.L., Neild S.A., Wagg D.J., 2014, Bifurcations of backbone curves for systems of coupled nonlinear two mass oscillator Nonlinear Dynamics, 77 (1–2) pp. 311-320, 10.1007/s11071-014-1295-3. CrossRefView Record in Scopus Google Scholar. |
| [4] | Wagg D.J., Neild S.A., 2009, Nonlinear Vibration with Control, Springer-Verlag, Berlin, Germany. Google Scholar. |
| [5] | Mariūnas M., 2020, Methods for Determining Resonant and Parametric Excitation Frequencies of Nonlinear Dynamic Systems. American Journal of Computational and Applied Mathematics, 10(1), pp.6 – 14. |
| [6] | Hill T.L., Cammarano A., Neild A., Wagg D.J., 20I5, Interpreting the forced responses of a two-degree-of-freedom nonlinear oscillator using backbone curves. Volume 349, 4, pp.276 – 288. |
| [7] | El - Bassiony A. F., Kamel M. M., Abdel-Khalik A., 2003, Two-to-one internal resonances in nonlinear two degree of freedom system with parametric and external excitations. Mathematics and Computers in Simulation, Volume 63, Issue 1, pp.45-56. |
| [8] | Vibration Reduction of Two Degree of Freedom Nonlinear System Subject to Parametric Excitation via Negative Feedback Velocity, 2019, Yasser A. Amer1 and Mai M. Agwa 2, Zagazig Egipt, Radoslaw Jedynak, Kazimierz Pulaski, Ismail Esen, Karabuk, ..., Konjuro Makihara, Dario Aristizabal-Ochoa J., Asian Reserch Journal of Mathematics, 12(1), pp. 1-21. |
| [9] | Tamas Kalmar – Nagy and Balakumar Balachandran, 2011, Forced harmonic vibration of a Duffing oscillator with linear viscous damping. The Duffing Equation: First Edition, Published John Willey and Sons, Ltd, ISBN: 978 – 0 – 470 – 71549, pp. 141-160. |
| [10] | Richard h. Rand., 2005, Lecture Notes on Nonlinear Vibrations. Depart. Theoretical and Applied Mechanics. Cornel University, Ithaca N.Y., 14853, rhr2@cornell.edu, p. 111, http://www.tam.cornell.edu/randdors/. |
| [11] | Pan SuL, Jiechang Wu2., Shuyong Liu3., 2018, Jian Jiang4, Study on the dynamics of two-degree-of-freedom system with variable stiffness magnetic isolator. Journal of Vibroengineering, Vol. 20, Issue 1, pp. 116-126. |
| [12] | Hua-Zhen An., Xiao-Dong Yang., Feng Liang., Wei Zhang., Tian-Zhi Yang and Yuan Ren., 2019, On Nonlinear Motions of Two-Degree-of-Freedom Nonlinear Systems with Repeated Linearized Natural Frequencies. International Journal of Bifurcation and Chaos, Vol. 29, No. 10, pp. 25-32. |



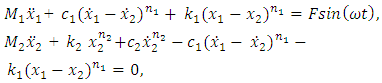
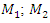 are masses of the system;
are masses of the system; 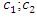 are coefficients of damping;
are coefficients of damping; 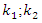 are coefficients of stiffness;
are coefficients of stiffness; 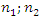 are exponents of
are exponents of 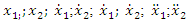 are velocities and accelerations; F is amplitude of external excitement force;
are velocities and accelerations; F is amplitude of external excitement force; 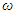 is angular frequency; t is time.
is angular frequency; t is time. 
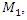 spring
spring 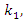 damping coefficient
damping coefficient 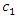 and external excitation force
and external excitation force 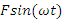 , and the other - with mass
, and the other - with mass 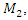 spring
spring  and the damping coefficient
and the damping coefficient 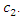 Thus, the system of equations (1) is rearranged as follows:
Thus, the system of equations (1) is rearranged as follows: 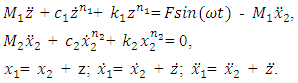
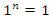 ), the nonlinear dynamic system becomes linear:
), the nonlinear dynamic system becomes linear: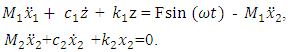
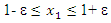 and
and 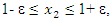 where ε magnitude is small enough.Evaluating the existing peculiarities of the force, stiffness and energy connection in a nonlinear dynamic system, using the method developed in [5], a system of three homogeneous equations is formed for the first subsystem:
where ε magnitude is small enough.Evaluating the existing peculiarities of the force, stiffness and energy connection in a nonlinear dynamic system, using the method developed in [5], a system of three homogeneous equations is formed for the first subsystem: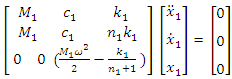
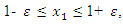 where
where 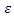 magnitude is small enough.The first row of the matrix (4) evaluates the effects of the force, the second – the effects of the stiffness and the third - of the energy connection peculiarities in a nonlinear dynamic system. From the system of homogeneous equations (4) it is determined that:
magnitude is small enough.The first row of the matrix (4) evaluates the effects of the force, the second – the effects of the stiffness and the third - of the energy connection peculiarities in a nonlinear dynamic system. From the system of homogeneous equations (4) it is determined that: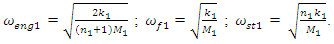
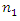 parameter increases, the frequency generated by the energy connection peculiarities decreases and the frequency generated by the stiffness connection peculiarities increases. Meanwhile, the frequency generated by the force connection peculiarities does not depend on the value of the
parameter increases, the frequency generated by the energy connection peculiarities decreases and the frequency generated by the stiffness connection peculiarities increases. Meanwhile, the frequency generated by the force connection peculiarities does not depend on the value of the 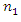 parameter.When
parameter.When 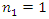 , then from the resonant frequency dependencies (5) of the considered subsystems we get that:
, then from the resonant frequency dependencies (5) of the considered subsystems we get that: 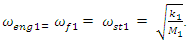
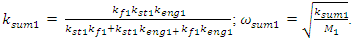
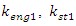 and
and 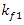 values are calculated according to expressions:
values are calculated according to expressions: 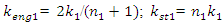 and
and 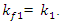 A system of linear homogeneous equations for the second subsystem is formed analogously:
A system of linear homogeneous equations for the second subsystem is formed analogously: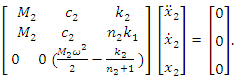
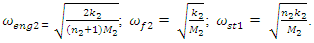
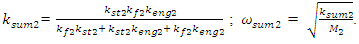
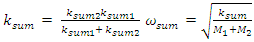
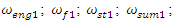
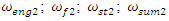 and
and 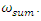 If the exponents of
If the exponents of 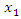 and
and 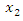 are equal
are equal 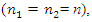 then the number of resonant frequencies in the system (1) will not change, but some values will change, because a multiplier n is used instead of
then the number of resonant frequencies in the system (1) will not change, but some values will change, because a multiplier n is used instead of 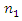 and
and 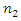 in equations (4) and (8).
in equations (4) and (8).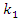 = 100000 N/m;
= 100000 N/m; 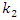 = 40000 N/m; F = 100000 N;
= 40000 N/m; F = 100000 N; 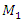 = 5.0 kg;
= 5.0 kg; 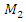 = 3.0 kg;
= 3.0 kg; 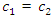 = 0.05, were calculated using formulas (5), (7-11). The following results were obtained:
= 0.05, were calculated using formulas (5), (7-11). The following results were obtained: 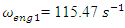 ;
; 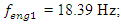
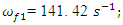
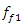 = 22.52 Hz;
= 22.52 Hz; 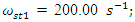
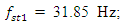
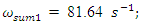
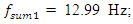
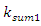 = 33325.12 N/m;
= 33325.12 N/m; 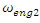 = 94.28
= 94.28  = 15.01 Hz;
= 15.01 Hz; 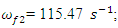
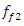 = 18.38 Hz;
= 18.38 Hz; 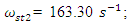
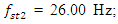
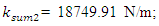
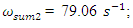
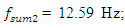
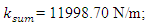
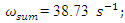
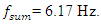 Analyzing the search graphs shown in Figure 2 and 4, we will notice when the system is excited at the frequency
Analyzing the search graphs shown in Figure 2 and 4, we will notice when the system is excited at the frequency 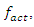 then the spectral density contains only a part of the calculation at the system resonant frequency. The other part of the resonant frequencies is covered by vibrations of higher intensity of the system. It should be noted that when
then the spectral density contains only a part of the calculation at the system resonant frequency. The other part of the resonant frequencies is covered by vibrations of higher intensity of the system. It should be noted that when 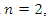 the system excites sufficiently large vibration amplitudes at a frequency of
the system excites sufficiently large vibration amplitudes at a frequency of 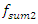 = 12.59 Hz (Figure 2), although it is exited at frequency
= 12.59 Hz (Figure 2), although it is exited at frequency 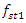 = 31.85 Hz. The magnitudes of the latter vibrations in time are modulated by frequency subharmonic
= 31.85 Hz. The magnitudes of the latter vibrations in time are modulated by frequency subharmonic 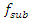 = 3.08 Hz of resonant frequency
= 3.08 Hz of resonant frequency 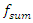 = 6.0 Hz. And this can be seen very clearly in the graphs provided in Figure 2. However, such vibrations in a nonlinear dynamic system occur only at the beginning, and after a few seconds they mainly vibrate at the excitation frequency. It is important to note that the analysis of nonlinear dynamic system initial vibrations allows to see the frequencies of the system subsystems and subharmonic frequencies. When a nonlinear dynamic system is excited by
= 6.0 Hz. And this can be seen very clearly in the graphs provided in Figure 2. However, such vibrations in a nonlinear dynamic system occur only at the beginning, and after a few seconds they mainly vibrate at the excitation frequency. It is important to note that the analysis of nonlinear dynamic system initial vibrations allows to see the frequencies of the system subsystems and subharmonic frequencies. When a nonlinear dynamic system is excited by 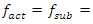 3.08 Hz, it generates high amplitude vibrations at the resonant frequency
3.08 Hz, it generates high amplitude vibrations at the resonant frequency 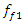 = 22.52 Hz (Figure 4) and it is modulated at a frequency of
= 22.52 Hz (Figure 4) and it is modulated at a frequency of 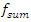 = 6.17 Hz, whereas
= 6.17 Hz, whereas 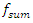 is 4 times repeated the system resonant
is 4 times repeated the system resonant 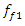 frequency. The subharmonic frequency
frequency. The subharmonic frequency 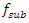 is approximately 7 times repeated and for the resonant frequency
is approximately 7 times repeated and for the resonant frequency 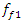 = 22.52 Hz as well, but the vibration intensity of the latter frequency is lower so it is practically not seen in the vibration graph of Figure 4. Therefore, the choice of operating modes and parameters of the system should not allow it to operate under resonant conditions.
= 22.52 Hz as well, but the vibration intensity of the latter frequency is lower so it is practically not seen in the vibration graph of Figure 4. Therefore, the choice of operating modes and parameters of the system should not allow it to operate under resonant conditions.
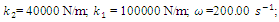
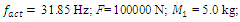
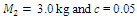
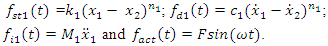
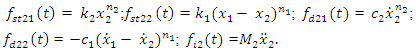

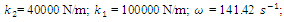
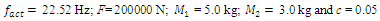
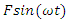 will excite vibrations
will excite vibrations 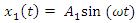 and
and 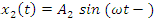 in the nonlinear two degree of freedom system. The dynamic system under consideration contains 9 different types of forces (12) and (13).In the first step, we will consider the frequencies of parametric vibration in the system (12) generated by stiffness, damping, inertia and external excitation forces. When
in the nonlinear two degree of freedom system. The dynamic system under consideration contains 9 different types of forces (12) and (13).In the first step, we will consider the frequencies of parametric vibration in the system (12) generated by stiffness, damping, inertia and external excitation forces. When 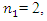 the force
the force 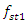 will be expressed as follows:
will be expressed as follows: 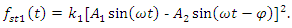
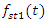 and
and 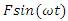 as follows:
as follows: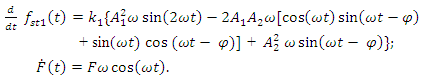
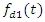 (12) we get the expression of damping force:
(12) we get the expression of damping force: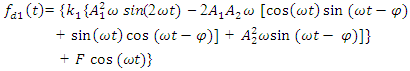
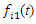 (12) we get the force of inertia, which excites the frequencies of parametric vibrations of the system:
(12) we get the force of inertia, which excites the frequencies of parametric vibrations of the system: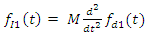

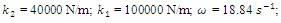
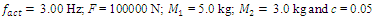
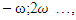 damping force
damping force 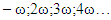 The frequencies generated by the forces under consideration are shown in Table 1 below.In this way, when n = 2, the system will generate parametric vibration with frequency:
The frequencies generated by the forces under consideration are shown in Table 1 below.In this way, when n = 2, the system will generate parametric vibration with frequency: 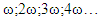 or the frequencies of parametric vibration generated in the system can be described as follows:
or the frequencies of parametric vibration generated in the system can be described as follows: 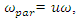 when u = 1;2;3;4… By performing analogous steps we will determine the frequencies of parametric vibrations generated in the second subsystem and when
when u = 1;2;3;4… By performing analogous steps we will determine the frequencies of parametric vibrations generated in the second subsystem and when 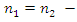 parametric vibration of the same frequencies generated in the second subsystem.
parametric vibration of the same frequencies generated in the second subsystem. 
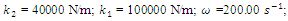
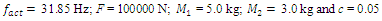
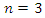 then we will write the expression of stiffness force as follows:
then we will write the expression of stiffness force as follows: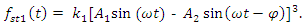
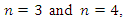 then the expressions of the velocities and accelerations of force changes become long and uninformative, therefore they expressions are not presented in this paper.However, graphs of their regularity of change are shown in Figure 6a and b.
then the expressions of the velocities and accelerations of force changes become long and uninformative, therefore they expressions are not presented in this paper.However, graphs of their regularity of change are shown in Figure 6a and b. 
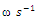
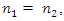 the exponents of the variables of
the exponents of the variables of 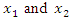 and their combinations determine the regularity of the change of the parameter u and its dependence can be expressed as follows:
and their combinations determine the regularity of the change of the parameter u and its dependence can be expressed as follows: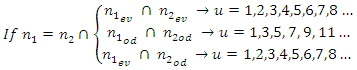
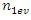 and
and 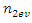 are even numbers;
are even numbers; 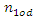 and
and 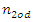 - odd numbers;
- odd numbers; 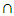 is conjunction;
is conjunction; 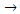 is implication.Then in the general case we will determine the frequencies of parametric vibration in a nonlinear system of two degrees of freedom as follows:
is implication.Then in the general case we will determine the frequencies of parametric vibration in a nonlinear system of two degrees of freedom as follows: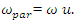
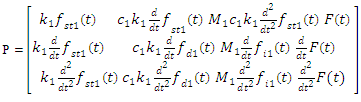
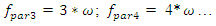 And the high-amplitude vibration of the frequency also generate parametric vibrations (Figure 1), but at different frequencies:
And the high-amplitude vibration of the frequency also generate parametric vibrations (Figure 1), but at different frequencies: 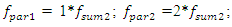
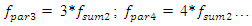 However, the resonant frequency
However, the resonant frequency 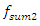 = 12.01 Hz (Figure 1b) generates parametric vibrations of significantly higher amplitude as compared to the vibrations excited by the external force. The results in Figure 3 show that the frequency
= 12.01 Hz (Figure 1b) generates parametric vibrations of significantly higher amplitude as compared to the vibrations excited by the external force. The results in Figure 3 show that the frequency 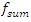 = 6.17 Hz significantly modulates the vibration when the nonlinear system excites at a frequency
= 6.17 Hz significantly modulates the vibration when the nonlinear system excites at a frequency 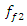 = 22.7 Hz, which corresponds to the frequency excited by the force connection peculiarities. Meanwhile, choosing the appropriate frequency of excitation force can significantly reduce vibration modulation and avoid nonlinear dynamic system pulsating vibration, for example, in the case discussed in Figure 2. In the example examined earlier, there is still an undesirable thing, such as
= 22.7 Hz, which corresponds to the frequency excited by the force connection peculiarities. Meanwhile, choosing the appropriate frequency of excitation force can significantly reduce vibration modulation and avoid nonlinear dynamic system pulsating vibration, for example, in the case discussed in Figure 2. In the example examined earlier, there is still an undesirable thing, such as 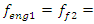 18.38 Hz. In addition, the system total frequency
18.38 Hz. In addition, the system total frequency 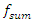 = 6.17 Hz is 5 times repeated the external excitation force frequency and three times repeated the
= 6.17 Hz is 5 times repeated the external excitation force frequency and three times repeated the 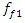 = 22.52 Hz frequency. Thus, by properly selecting the dynamic system parameters and the external excitation force frequency, the system vibration levels could be reduced. In this way, parametric vibration frequencies are generated not only by external excitation force, but also by high-amplitude vibrations of a nonlinear dynamic system. It is therefore necessary to emphasize that the vibrations generated by external forces may not always be greatest. If high amplitudes of vibration are excited in the system by other parametric frequencies, then the vibrations of the latter parametric frequencies will predominate in it, and the external excitation forces generated by the parametric vibration can almost be invisible. For the system with cubic nonlinearity whose parameters are:
= 22.52 Hz frequency. Thus, by properly selecting the dynamic system parameters and the external excitation force frequency, the system vibration levels could be reduced. In this way, parametric vibration frequencies are generated not only by external excitation force, but also by high-amplitude vibrations of a nonlinear dynamic system. It is therefore necessary to emphasize that the vibrations generated by external forces may not always be greatest. If high amplitudes of vibration are excited in the system by other parametric frequencies, then the vibrations of the latter parametric frequencies will predominate in it, and the external excitation forces generated by the parametric vibration can almost be invisible. For the system with cubic nonlinearity whose parameters are: 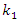 = 100000 N/m;
= 100000 N/m; 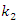 = 40000 N/m; F = 100000 N;
= 40000 N/m; F = 100000 N; 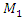 = 5.0 kg;
= 5.0 kg; 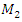 = 3.0 kg;
= 3.0 kg; 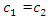 = 0.05, the resonant frequencies of the system were calculated using the formulas (5), (7), (9), (10), (11). The following results were obtained:
= 0.05, the resonant frequencies of the system were calculated using the formulas (5), (7), (9), (10), (11). The following results were obtained: 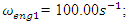
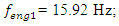
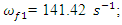
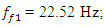
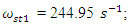
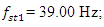
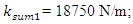
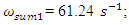
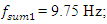
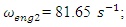
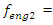
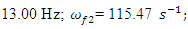
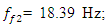
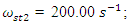
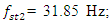
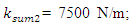
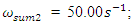
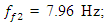
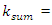
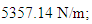
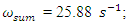
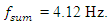 The spectra of vibrations of masses
The spectra of vibrations of masses 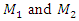 are shown in Figures 7a and b. The results of the study show that the frequency of parametric vibrations in the system changes according to the analytically determined dependence (20). Dynamic system with cubic nonlinearity is more robust than quadratic nonlinearity systems and extremely high vibration modulation at some frequencies is not observed.The spectrum of masses
are shown in Figures 7a and b. The results of the study show that the frequency of parametric vibrations in the system changes according to the analytically determined dependence (20). Dynamic system with cubic nonlinearity is more robust than quadratic nonlinearity systems and extremely high vibration modulation at some frequencies is not observed.The spectrum of masses 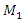 (Figure 7b) shows a small peak at a very low frequency
(Figure 7b) shows a small peak at a very low frequency 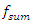 = 4.69 Hz, which is the vibration frequency generated by the total stiffness of the system.
= 4.69 Hz, which is the vibration frequency generated by the total stiffness of the system. 
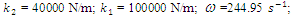
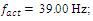
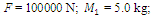
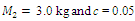
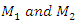 are shown in Figure 8. When n = 2, then the phase – space diagrams are very uninformative, therefore they are not presented in this paper.
are shown in Figure 8. When n = 2, then the phase – space diagrams are very uninformative, therefore they are not presented in this paper.
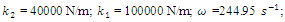
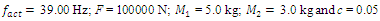
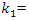 100000 N/m;
100000 N/m; 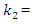 40000 N/m; F = 100000 N;
40000 N/m; F = 100000 N; 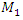 = 5.0 kg;
= 5.0 kg; 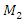 = 3.0 kg;
= 3.0 kg; 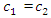 = 0.05, a system frequency which evaluate the stiffness connection peculiarities in a nonlinear dynamic system was determined:
= 0.05, a system frequency which evaluate the stiffness connection peculiarities in a nonlinear dynamic system was determined: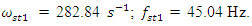 The spectrum of the second mass vibrations for the latter frequency is shown in Figure 9. It can be seen that the spectral density contains all frequencies of parametric vibration as determined analytically, and secondly, for even numbers of the parameter u the spectral intensity is much lower. An analogous vibration spectrum was determined for the first mass of the system as well.
The spectrum of the second mass vibrations for the latter frequency is shown in Figure 9. It can be seen that the spectral density contains all frequencies of parametric vibration as determined analytically, and secondly, for even numbers of the parameter u the spectral intensity is much lower. An analogous vibration spectrum was determined for the first mass of the system as well.
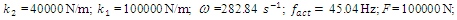
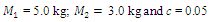
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML