Mečislovas Mariūnas
Department of Biomechanical Engineering, Vilnius Gediminas Technical University, Vilnius LT, Lithuania
Correspondence to: Mečislovas Mariūnas, Department of Biomechanical Engineering, Vilnius Gediminas Technical University, Vilnius LT, Lithuania.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
This paper presents methods for determining resonant and parametric excitation frequencies in a nonlinear single-degree-of-freedom dynamic system. The results show that in nonlinear dynamic system there are four groups of resonant frequencies, which are defined by energy, force, stiffness connection peculiarities, as well as the total stiffness of the system. The results also demonstrate that the system generates a very wide spectrum of parametric excitation frequencies, such that when they coincide with the resonant frequency the level of system vibrations increases significantly. By setting the parameters of the system (stiffness, mass, damping, etc.), we determine its resonant frequencies, however the frequency and number of parametric vibrations of a dynamic system depend on the level of nonlinearity of the system. Thus, the frequency of parametric vibration is independent of their amplitude. The certainty of the analytical methods presented in the article was verified by numerical calculations.
Keywords:
Methods for determination of resonant and parametric frequencies, Nonlinear dynamic system, Quadratic, Cubic and fourth order nonlinearities, Vibration
Cite this paper: Mečislovas Mariūnas, Methods for Determining Resonant and Parametric Excitation Frequencies of Nonlinear Dynamic Systems, American Journal of Computational and Applied Mathematics , Vol. 10 No. 1, 2020, pp. 6-14. doi: 10.5923/j.ajcam.20201001.02.
1. Introduction
In order to create a nonlinear mechanical dynamic system and ensure its sustained and stable operation, safe working conditions need to be determined. This can be achieved at the design stage by establishing the resonant frequencies of nonlinear vibration, and also the proper operating modes of the system. Resonance is a known concept in linear system analysis and its study is important in many branches of engineering. At a particular resonance the frequency of an exciting force matches the natural frequency of the system, with the result that energy transmission is efficient and the amplitude of vibration becomes significant. Scientific works [1-16] were used as the basis for the investigation of vibration of nonlinear mechanical systems and their resonant frequencies. In many cases, however, theoretical analysis is performed by applying approximate or numerical methods. For example, in [1,2,13-16], nonlinear dynamic systems were analyzed using analytical and numerical methods. In the course of analyzing the vibrations of system using numerical methods, their spectral density was determined, and it was observed that in some cases vibrations were generated by repeated frequencies of external excitement [2]. The power spectral density of the system response shows multiple peaks at frequencies in the proportion of 1: 3: 5… These determined harmonics and subharmonics in the response of a nonlinear system. Strong and weak resonances in delayed systems were analyzed [11,12,14]. The analytical results are compared with those obtained from numerical integration. The stability of the periodic responses of the system is examined using the frequency response function and the phase – plane methods [3,15,16]. The behavior of nonlinear dynamic mechanical systems impacted by different external excitation frequency was examined and the parametric vibrations were analyzed [5-8,14-15]. Numerical integration was carried out to verify the theoretical predictions obtained. For the analysis of nonlinear dynamical systems many researchers used harmonic balance, modal interactions and other approximate methods. In the case of Hegazy U.H. et al. [3] approximate solutions were obtained using the multiple scales perturbation technique. In [15,16] the stability of the Duffing oscillator of fixed points (x = 0, ±1) was analyzed by linearizing the equations. Moreover, using the harmonic balance method, a frequency response equation was derived which describes the amplitude of a steady state response of the equation at a given frequency of excitation. Whilst the resonant frequencies of the system determined in this way are not sufficiently accurate, an analysis of the literature suggests there is no exact method for determining the system’s resonant frequencies. In short, the approximate methods used do not explain the physics of vibration of nonlinear dynamical systems. Moreover, they do not show the specificity of their behavior compared to linear systems. Thus, the purpose of the research was to study the physics of vibration of nonlinear single-degree-of-freedom dynamic systems, to explain their features, to provide methods for determining the resonant and parametric excitation frequencies of the system, to clarify the frequencies of internal excitation, generated through the properties of the nonlinear dynamic system itself, and to show their destructive effects on the vibration level of the system.
2. Resonant Frequency of the System
The motion of a nonlinear single-degree-of-freedom dynamical system is described by the following differential equation: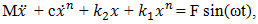 | (1) |
where M is mass of the system; c is coefficient of damping; 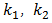 are coefficients of stiffness; n is the exponent of
are coefficients of stiffness; n is the exponent of 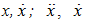 is acceleration and velocity; F is amplitude of external excitement force;
is acceleration and velocity; F is amplitude of external excitement force; 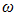 is angular frequency; t is time. It is known that the kinetic energy of the system of motion is equal to its potential energy:
is angular frequency; t is time. It is known that the kinetic energy of the system of motion is equal to its potential energy: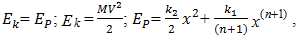 | (2) |
where 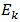 and
and 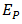 are kinetic and potential energies,
are kinetic and potential energies, 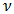 is velocity.With regard to dependence (1), we found that when the amplitude of the vibration becomes equal to one (x = 1), the differential equation of the motion of a nonlinear system (1) becomes linear, because the unit raised in n degrees is equal to one
is velocity.With regard to dependence (1), we found that when the amplitude of the vibration becomes equal to one (x = 1), the differential equation of the motion of a nonlinear system (1) becomes linear, because the unit raised in n degrees is equal to one 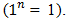 Accordingly, the equation (1), where the value of x is equal to or very close to one, will be expressed as follows:
Accordingly, the equation (1), where the value of x is equal to or very close to one, will be expressed as follows: 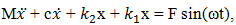 | (3) |
when 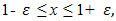 where
where 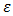 magnitude is small enough.Using the method of solving the linear differential equations of non-damped systems we obtained:
magnitude is small enough.Using the method of solving the linear differential equations of non-damped systems we obtained: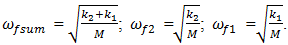 | (4) |
The resonant frequency is less than the frequency of the non-damped system. The expressions (4) show that there are three resonant frequencies (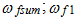 and
and 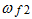 ) in the system caused by force connection peculiarities. After considering the system linearity, we will form an additional equation for the description of the motion of that system using its stiffness characteristics
) in the system caused by force connection peculiarities. After considering the system linearity, we will form an additional equation for the description of the motion of that system using its stiffness characteristics 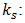
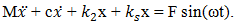 | (5) |
Stiffness 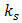 is determined as follows:
is determined as follows: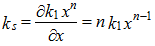 and when x =1 then
and when x =1 then 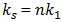 . Equation (5) helped to determine the three resonant system’s frequencies caused by peculiarities of the stiffness connections of the system:
. Equation (5) helped to determine the three resonant system’s frequencies caused by peculiarities of the stiffness connections of the system: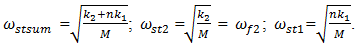 | (6) |
When x = 1, the kinetic and potential energy of the system (2) will be calculated as follows: 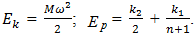 Using the kinetic and potential energy equality condition we then obtain:
Using the kinetic and potential energy equality condition we then obtain: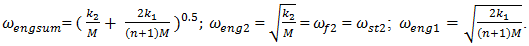 | (7) |
Thus, to determine the resonant frequencies of a single-degree-of-freedom nonlinear dynamic system, we must create and solve a system of linear homogeneous equations: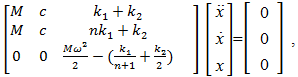 | (8) |
when 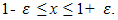 If the dynamic system has energy, force and stiffness connection peculiarities, then the total stiffness of the system will also be the magnitude, which will be evaluated as follows:
If the dynamic system has energy, force and stiffness connection peculiarities, then the total stiffness of the system will also be the magnitude, which will be evaluated as follows: 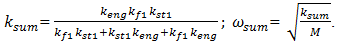 | (9) |
where 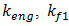 and
and  are coefficient of stiffness, caused by energy, force and stiffness connection peculiarities.Expression (9) is only valid when
are coefficient of stiffness, caused by energy, force and stiffness connection peculiarities.Expression (9) is only valid when 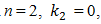 and when n = 2 or n > 2 and
and when n = 2 or n > 2 and 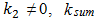 expression are complex and therefore are not included in this article. However, the total stiffness of the system shall in all cases be determined in the same way as for n = 2 and
expression are complex and therefore are not included in this article. However, the total stiffness of the system shall in all cases be determined in the same way as for n = 2 and 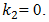 The investigation showed that there are four types of resonant frequency groups in the systems under consideration, which are caused by energy, force, stiffness connections peculiarities and by system total stiffness. Thus, there are 8 different frequencies
The investigation showed that there are four types of resonant frequency groups in the systems under consideration, which are caused by energy, force, stiffness connections peculiarities and by system total stiffness. Thus, there are 8 different frequencies 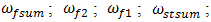
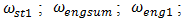
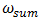 in systems. When
in systems. When 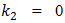 then only four resonant frequencies:
then only four resonant frequencies: 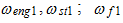 and
and 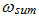 will be in the system. From expressions (4), (6-7) and (9) we observe that the resonant frequency is considerably lower than other ones which are defined by energy, power and stiffness connection peculiarities. Let us consider frequencies ratio:
will be in the system. From expressions (4), (6-7) and (9) we observe that the resonant frequency is considerably lower than other ones which are defined by energy, power and stiffness connection peculiarities. Let us consider frequencies ratio: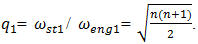 | (10) |
The system’s resonant frequencies, which are defined by the force connection peculiarities (4), are not dependent on the exponent of polynomial degree. An indicator that shows the number of the frequency generated by the force connection peculiarities is higher than the frequency generated by energy connection can be calculated as follows: 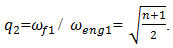 | (11) |
In this way, as the exponent of the polynomial increases, the frequencies described by the peculiarities of stiffness connections also increase, whereas energy frequency decreases. In this case, when the system will be resonant the magnitude of amplitude is calculated using the following formula: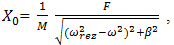 | (12) |
where 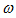 is angular frequency of external excitation force;
is angular frequency of external excitation force; 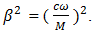 A common case
A common case 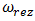 value is calculated according to expression
value is calculated according to expression 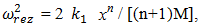 or
or 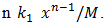
3. Parametric Excitation Frequency of the System
To investigate the resonant and parametric frequencies of the system, and verify the obtained analytical results, the Runge–Kutta methods of numerical analysis was performed. Systems with quadratic, cubic and fourth order nonlinearities were examined. The resonant frequencies of the system with the quadratic nonlinearity, who’s the system parameters are: 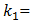 100000 N/m;
100000 N/m; 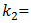 0.0; F = 100000 N; M = 5.0 kg and c = 0.05, were calculated using formulas (4-6), (7,9). The following results were obtained:
0.0; F = 100000 N; M = 5.0 kg and c = 0.05, were calculated using formulas (4-6), (7,9). The following results were obtained: 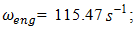
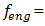
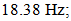
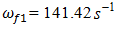
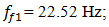
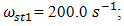
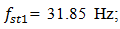
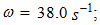
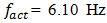 and
and 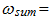
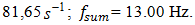
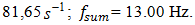 Figure 1b shows that the first peak of the highest intensity is an external acting force
Figure 1b shows that the first peak of the highest intensity is an external acting force 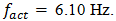 The second peak f = 18.39 Hz corresponds to the frequency generated by the energy connection peculiarities. In this case, the peak of spectral density described with force connections peculiarities
The second peak f = 18.39 Hz corresponds to the frequency generated by the energy connection peculiarities. In this case, the peak of spectral density described with force connections peculiarities 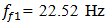 is smaller because of intensive vibration on the resonant frequencies,
is smaller because of intensive vibration on the resonant frequencies, 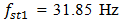 and
and 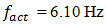 of the system. The very significant increase in the system vibration level at the excitation frequency
of the system. The very significant increase in the system vibration level at the excitation frequency 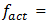
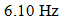 can be explained by the fact that the latter frequency almost coincides with the system frequency of total stiffness subharmonic frequency
can be explained by the fact that the latter frequency almost coincides with the system frequency of total stiffness subharmonic frequency 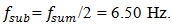 At spectral density in Figure 1b has a maximum vibration level at
At spectral density in Figure 1b has a maximum vibration level at 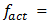
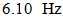 and
and 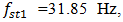 so in Figure 1a, only the vibration waves of
so in Figure 1a, only the vibration waves of 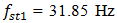 are visible on the low frequency curve
are visible on the low frequency curve 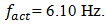 However, at spectral density (Figure 1b) still has lower intensity frequencies at 30;43 and other frequencies and they are not peaks of resonant frequencies. To clarify the nature of the abovementioned frequencies, let us consider the frequencies of parametric vibration in nonlinear dynamical system.
However, at spectral density (Figure 1b) still has lower intensity frequencies at 30;43 and other frequencies and they are not peaks of resonant frequencies. To clarify the nature of the abovementioned frequencies, let us consider the frequencies of parametric vibration in nonlinear dynamical system.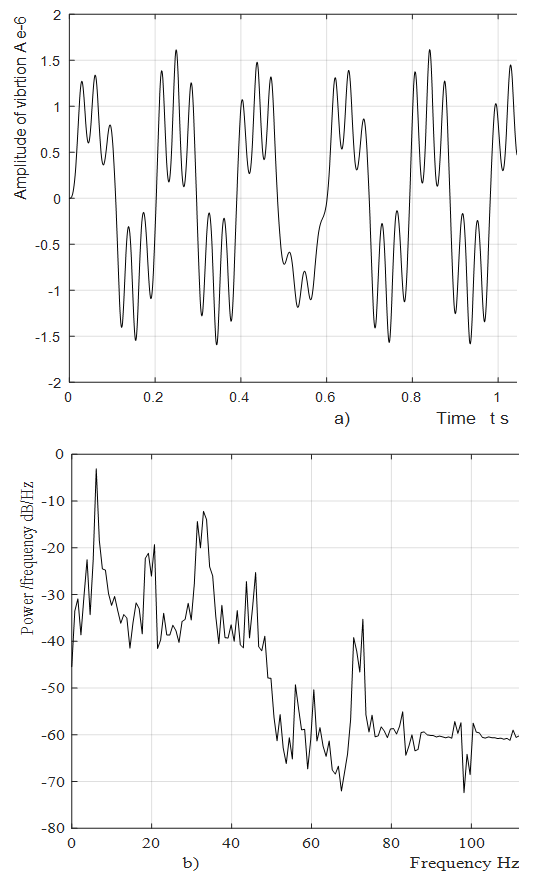 | Figure 1. Result of solution of vibration and spectral density for quadratic nonlinearity when  Hz; F = 100000 N; M = 5.0 kg and c= 0.5 Hz; F = 100000 N; M = 5.0 kg and c= 0.5 |
The resonant conditions in the system will only be when 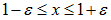 (and only then) that (12) dependency will be valid. Otherwise, it is not possible so simple to express the nonlinear dynamical system vibration dependence on its parameters. However, the latter expression shows that as the amplitude of the vibration increases (when x > 1), the denominator should increase and the amplitude of the vibration than should decrease. Thus, to some degree the nonlinear dynamic system should dampen its vibrations. Moreover, due to its nonlinearity, the vibrating system can generate additional frequency which is called parametric vibration frequencies. To determine these let us consider changes in the velocity and acceleration of stiffness, damping, and inertia forces of nonlinear dynamic system under the influence of the external excitation force F(t) = F sin(ωt).Let us suppose that the aforementioned force will excite vibrations x(t) = A sin (ωt).The dynamic system (1) under consideration contains 4 different types of forces: external excitation, stiffness, damping, and inertia. When n = 1, the forces mentioned above will be such expressions:
(and only then) that (12) dependency will be valid. Otherwise, it is not possible so simple to express the nonlinear dynamical system vibration dependence on its parameters. However, the latter expression shows that as the amplitude of the vibration increases (when x > 1), the denominator should increase and the amplitude of the vibration than should decrease. Thus, to some degree the nonlinear dynamic system should dampen its vibrations. Moreover, due to its nonlinearity, the vibrating system can generate additional frequency which is called parametric vibration frequencies. To determine these let us consider changes in the velocity and acceleration of stiffness, damping, and inertia forces of nonlinear dynamic system under the influence of the external excitation force F(t) = F sin(ωt).Let us suppose that the aforementioned force will excite vibrations x(t) = A sin (ωt).The dynamic system (1) under consideration contains 4 different types of forces: external excitation, stiffness, damping, and inertia. When n = 1, the forces mentioned above will be such expressions: 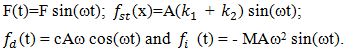 | (13) |
The first (velocity) and the second (acceleration) derivative of forces (13) will be: 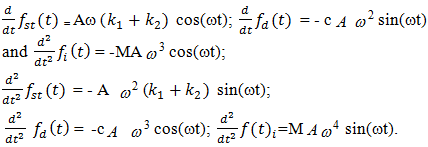 | (14) |
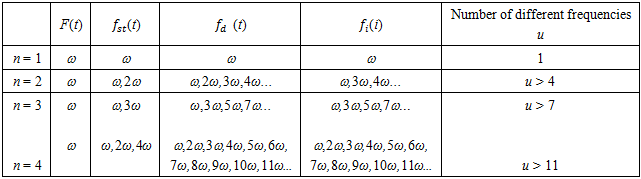
It can be seen from (13) and (14) that in a linear dynamic system the velocities and acceleration frequencies of the latter forces are the same as those of the external excitation force frequency ω.Table 1. The frequencies of velocity and accelerations of the forces acting on the system
 |
| |
|
These are shown in the table of velocity and acceleration frequencies (Table 1). Since the nonlinear dynamic system is considered, the superposition principle does not apply. Therefore, it is necessary to examine the cumulative effects of forces on the system. When n = 2 then the forces acting on the system will be as follows: 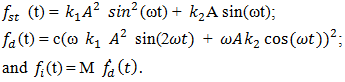 | (15) |
The velocity and accelerations of latter forces will be: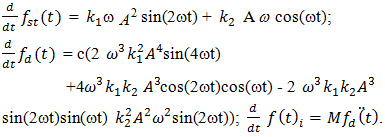 | (16) |
Similarly, velocities and accelerations of other forces at n > 2 can be found. Due to the complex expressions of the velocities and accelerations, we do not discuss them further in this paper. Analyzing the expressions of force, velocity and acceleration (15), (16) we find that when n = 2, the vibrating system will generate parametric frequencies: stiffness force 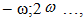 damping force
damping force 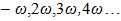 What the frequencies generated by the forces under consideration are shown in (Table 1). In this way, when n = 2, the system will generate parametric vibration with frequency:
What the frequencies generated by the forces under consideration are shown in (Table 1). In this way, when n = 2, the system will generate parametric vibration with frequency: 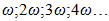 or the parametric frequencies generated in the system can be described as follows:
or the parametric frequencies generated in the system can be described as follows: 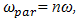 when u = 1;2;3;4… When n = 3, using the above method we get that
when u = 1;2;3;4… When n = 3, using the above method we get that 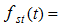
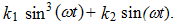 The latter expression shows that stiffness force will generate
The latter expression shows that stiffness force will generate 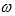 and
and 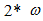 parametric frequencies in the dynamic system. Damping force and their velocity generous
parametric frequencies in the dynamic system. Damping force and their velocity generous 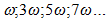 parametric frequencies (Figure 2a). So when the n = 3 parameter u gets the following values: u = 1;3;5;7... When n = 4, the damping force spectrum is shown in Figure 2b.
parametric frequencies (Figure 2a). So when the n = 3 parameter u gets the following values: u = 1;3;5;7... When n = 4, the damping force spectrum is shown in Figure 2b.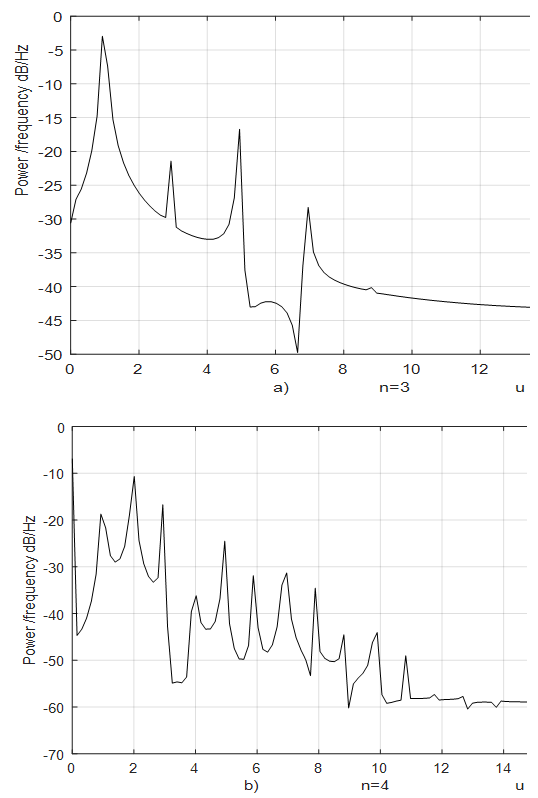 | Figure 2. Spectral density for the damping force, when 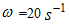 with frequencies, whose value is determined by (17) with frequencies, whose value is determined by (17) |
In this way, when n is an even number in a nonlinear dynamic system will be also generated parametric vibrations.Equations (13 - 16) show only a fraction of the frequencies generated by velocity and acceleration forces in a nonlinear dynamic system. All frequencies generated by a nonlinear dynamic system are described in a conditionally called matrix - table (18).That way, when n >1 and it is an even and odd number, the vibration of a nonlinear dynamic system will generate parametric vibrations, the frequencies of which will be determined as follows: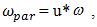 | (17) |
where u = 1;2;3;4;5;6;7;8;9... for even n and u = 1;3;5;7... for odd n.If the exponents of stiffness and damping forces are not equal, then the regularity of the change of the u parameter will be determined by the product of the latter indices.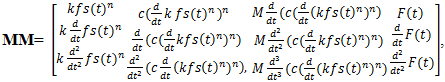 | (18) |
where 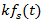 – is the conditional notation of the cumulative effect of the stiffness force on the dynamic system.The analysis of (13-16,17) the dependencies, as well as the data in Table 1 and Figure 2 shows that:when dynamic system n = 1, it does not generate additional frequency parametric vibration;when dynamic systems n >1, it generates parametric vibration of additional frequencies and the higher the value of the n parameter the more they will be generated; in the dynamical system, as the values of the parametric frequencies increase, the amplitudes of the vibration decrease significantly (Figure 2);the results of the study showed that the frequency of parametric vibration is independent of their amplitude; their number and magnitude depend on the parameters of the nonlinearity of the dynamic system;the generated parametric vibration frequencies in a nonlinear dynamical system can be estimated (evaluated) by members of first row of the matrix–table MM. Thus, these studies demonstrate that the nonlinear dynamic system has resonant and parametric vibration frequencies, and identified analytical ways to determine them.
– is the conditional notation of the cumulative effect of the stiffness force on the dynamic system.The analysis of (13-16,17) the dependencies, as well as the data in Table 1 and Figure 2 shows that:when dynamic system n = 1, it does not generate additional frequency parametric vibration;when dynamic systems n >1, it generates parametric vibration of additional frequencies and the higher the value of the n parameter the more they will be generated; in the dynamical system, as the values of the parametric frequencies increase, the amplitudes of the vibration decrease significantly (Figure 2);the results of the study showed that the frequency of parametric vibration is independent of their amplitude; their number and magnitude depend on the parameters of the nonlinearity of the dynamic system;the generated parametric vibration frequencies in a nonlinear dynamical system can be estimated (evaluated) by members of first row of the matrix–table MM. Thus, these studies demonstrate that the nonlinear dynamic system has resonant and parametric vibration frequencies, and identified analytical ways to determine them.
4. Numerical Analysis and Discussion
When the nonlinear dynamic system vibrates, all resonant frequencies will get in it, although the magnitude of their vibrations will not be the same (Figure 1a and b). Hence, the level of vibration will be higher for those resonant frequencies where the frequency of external excitation force will be repeated. If the ratio of system resonant and external excitation frequencies is an integer or close to it, then on the main vibration wave will be clearly seen 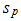 times higher frequency wave (Figure 1a). The value of the
times higher frequency wave (Figure 1a). The value of the 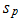 is calculated as follows:
is calculated as follows: 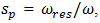 | (19) |
where 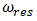 is the system's resonant frequency. Figure 1b clearly shows that the level of the vibration of the resonant frequency
is the system's resonant frequency. Figure 1b clearly shows that the level of the vibration of the resonant frequency 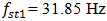 is high enough and sp ratio magnitude for that frequency is approximately (31.85/6.10 = 5.21) 5 times greater than the external excited frequency
is high enough and sp ratio magnitude for that frequency is approximately (31.85/6.10 = 5.21) 5 times greater than the external excited frequency 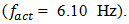 It follows that the wave of resonant vibration (which is defined by stiffness connection peculiarities) will be observed on the wave of the external excitation vibration. In the considering case also
It follows that the wave of resonant vibration (which is defined by stiffness connection peculiarities) will be observed on the wave of the external excitation vibration. In the considering case also 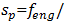
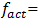 18.39/6.10 = 3.015. It means that the frequency of the
18.39/6.10 = 3.015. It means that the frequency of the 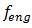 vibration wave on the external excitation vibration wave should repeat approximately 3 times. Yet, the intensity of 18.39 Hz frequency vibration in the spectral density of Figure 1b is significantly lower. When the dynamic system is exciting at the highest resonant frequency
vibration wave on the external excitation vibration wave should repeat approximately 3 times. Yet, the intensity of 18.39 Hz frequency vibration in the spectral density of Figure 1b is significantly lower. When the dynamic system is exciting at the highest resonant frequency 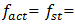 31.85 Hz we get almost concentric ellipses in the phase – space diagram (Figure 3a). It can be seen from the Figure 3b that vibrations of small amplitudes at
31.85 Hz we get almost concentric ellipses in the phase – space diagram (Figure 3a). It can be seen from the Figure 3b that vibrations of small amplitudes at 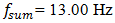 and lower frequencies are excited in the dynamic system. It is important to note that the 13.00 Hz vibration frequency corresponds to the calculated total frequency of the system. The spectral density of the oscillations (Figure 3b) also shows that high intensity parametric vibrations are excited at a frequency of
and lower frequencies are excited in the dynamic system. It is important to note that the 13.00 Hz vibration frequency corresponds to the calculated total frequency of the system. The spectral density of the oscillations (Figure 3b) also shows that high intensity parametric vibrations are excited at a frequency of 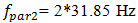 and lower intensity parametric vibration at frequency
and lower intensity parametric vibration at frequency 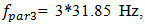
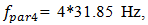 and
and 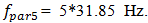 The research showed that at higher excitation forces, the amplitudes of
The research showed that at higher excitation forces, the amplitudes of 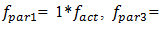
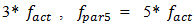 of the parametric vibration frequencies become larger than when the system vibrates at these
of the parametric vibration frequencies become larger than when the system vibrates at these 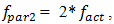
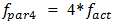
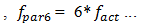 frequencies.
frequencies. 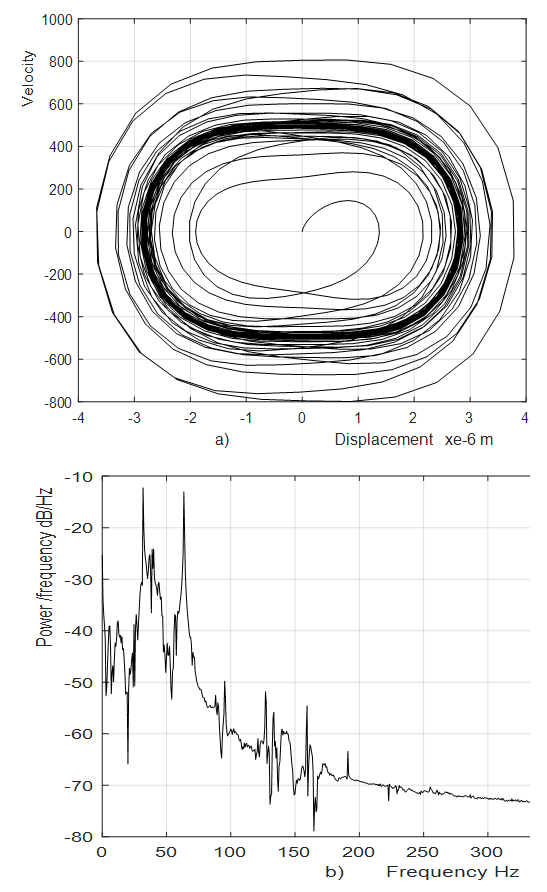 | Figure 3. Results of research for the quadratic nonlinearity of the system when 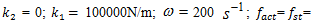 31.85Hz; M = 5.0kg 31.85Hz; M = 5.0kg |
For the system with cubic nonlinearity whose parameters are: 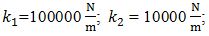 F =100000 N; M = 5.0 kg and c = 0.05, the resonant frequencies of the system were calculated using the formulas (4), (6), (7), (9). The following results were obtained:
F =100000 N; M = 5.0 kg and c = 0.05, the resonant frequencies of the system were calculated using the formulas (4), (6), (7), (9). The following results were obtained: 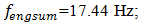
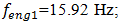
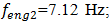
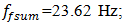
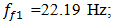
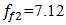
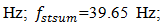
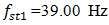 and
and 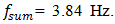 The calculation results of spectral density are shown in Figure 4a. The phase – space diagram in Figure 4b shows that the dynamic system vibrates at a resonant frequency, and that there are approximately
The calculation results of spectral density are shown in Figure 4a. The phase – space diagram in Figure 4b shows that the dynamic system vibrates at a resonant frequency, and that there are approximately 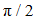 radians between phases of the displacement and velocity and behaves like a linear system.
radians between phases of the displacement and velocity and behaves like a linear system.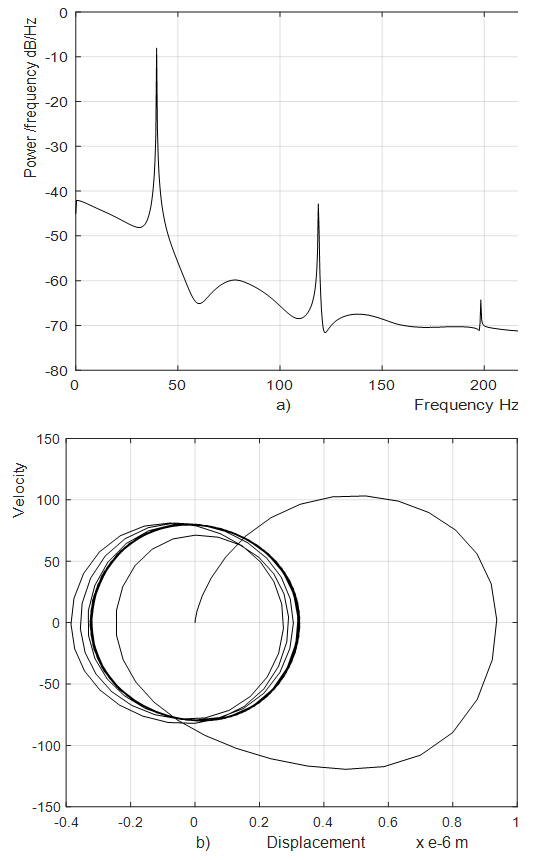 | Figure 4. Results of research for the cubic nonlinearity of the system when acting force frequency 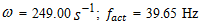 coincides with resonant frequency of the system coincides with resonant frequency of the system 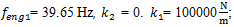 F = 200000 N, M = 5.0 kg F = 200000 N, M = 5.0 kg |
Figure 4a shows the three main frequencies, one of which is determined by stiffness connection peculiarities 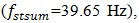 the less significant the second, and the third is determined by the parametric excitation frequencies:
the less significant the second, and the third is determined by the parametric excitation frequencies: 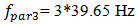 and
and 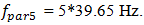 The significant amplitude of the system’s vibration is caused by the external exciting force which frequency coincide with the system resonant frequency
The significant amplitude of the system’s vibration is caused by the external exciting force which frequency coincide with the system resonant frequency 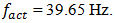 The amplitudes of the lower frequency vibrations are small, because they are invisible in their spectral density Figure 4a.Therefore, the spectral density graph (Figure 4a) shows only the frequencies
The amplitudes of the lower frequency vibrations are small, because they are invisible in their spectral density Figure 4a.Therefore, the spectral density graph (Figure 4a) shows only the frequencies 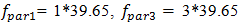 and
and 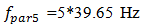 of the parametric vibrations. Thus, the computational results confirm that when n =2;3 and 4, the dynamic system generates the parametric vibration frequencies according to the determined regularities (17). In the case,
of the parametric vibrations. Thus, the computational results confirm that when n =2;3 and 4, the dynamic system generates the parametric vibration frequencies according to the determined regularities (17). In the case, 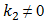 where the external excitation frequency coincides with the system's resonant frequency
where the external excitation frequency coincides with the system's resonant frequency 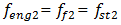 , the resonance conditions in the system will take place when x = 0. The vibration in the system with the cubic nonlinearity at the
, the resonance conditions in the system will take place when x = 0. The vibration in the system with the cubic nonlinearity at the 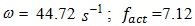
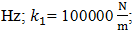
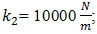 F = 100000 N; M = 5.0 kg and c = 0.05 are shown in Figure 5a and their spectral density – in Figure 5b. By calculating
F = 100000 N; M = 5.0 kg and c = 0.05 are shown in Figure 5a and their spectral density – in Figure 5b. By calculating 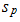 values according the expression (19), we find that
values according the expression (19), we find that 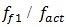 = 22,19/7,12 = 3,12. This means that the frequency defined by the force connection peculiarities is approximately 3 times higher than the external excitation frequency. Hence, in Figure 5a, three higher frequency waves are clearly visible on the low frequency vibration wave. In a spectral density (Figure 5b), we will observe resonant frequencies: 7.12;23.62;39.0 Hz and other parametric frequencies calculated using the analytical method. But when the frequency of the external force coincides with the system's resonant frequency
= 22,19/7,12 = 3,12. This means that the frequency defined by the force connection peculiarities is approximately 3 times higher than the external excitation frequency. Hence, in Figure 5a, three higher frequency waves are clearly visible on the low frequency vibration wave. In a spectral density (Figure 5b), we will observe resonant frequencies: 7.12;23.62;39.0 Hz and other parametric frequencies calculated using the analytical method. But when the frequency of the external force coincides with the system's resonant frequency 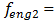 7.12 Hz, then the magnitude of the vibration of that frequency significantly increases and covers smaller amplitudes of vibrations of other frequencies. Therefore, we cannot see vibration of all frequencies of the system in Figure 5a and b.
7.12 Hz, then the magnitude of the vibration of that frequency significantly increases and covers smaller amplitudes of vibrations of other frequencies. Therefore, we cannot see vibration of all frequencies of the system in Figure 5a and b.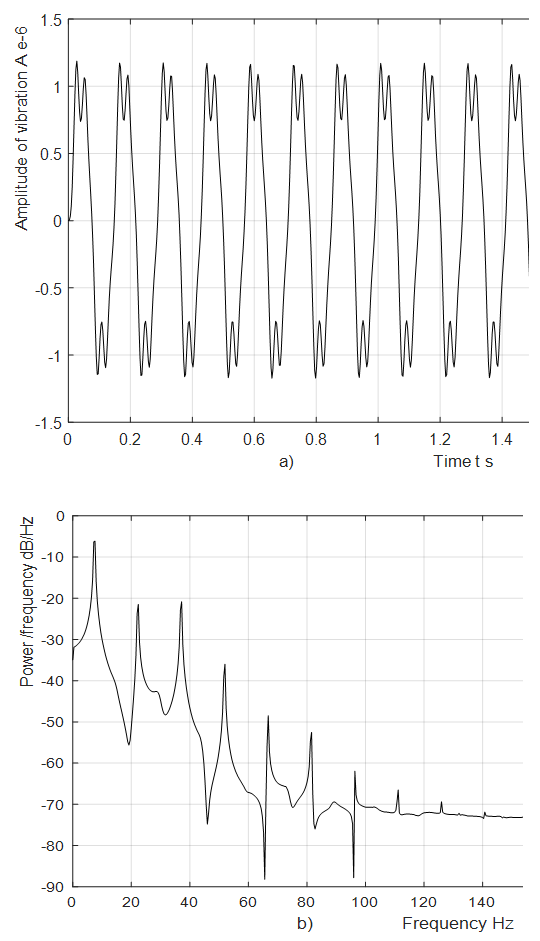 | Figure 5. Amplitude of vibration and spectral density when 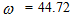 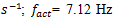 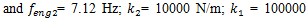 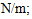 F= 100000 N; M = 5.0 kg F= 100000 N; M = 5.0 kg |
The last example shows two errors in the parameters of the setting system and the frequency of external excitement force. First, the external force excitation frequency coincided with the system's resonant frequency 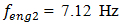 and second, the system parametric excitation frequency
and second, the system parametric excitation frequency 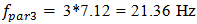 is close to the force connection peculiarities determined frequency
is close to the force connection peculiarities determined frequency 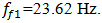 The resonant and parametric excitation frequencies were studied for other parameters of the system, for example:
The resonant and parametric excitation frequencies were studied for other parameters of the system, for example: 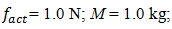
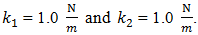 It is important to note that when n = 2;3 and 4 are subharmonics at their vibration and velocity spectral densities, which the frequencies are twice less the total stiffness frequency of the system (6.50 Hz at n = 2 and 1.92 Hz at n = 3).Subharmonic vibrations at f = 6.50 Hz are clearly visible in Figure 3b and at 1.92 Hz – in Figure 1b. Further research may clarify their origin. For the analyzed dynamic system, the results of which are presented in Figure 3, it was enough to change only the external excitation frequency
It is important to note that when n = 2;3 and 4 are subharmonics at their vibration and velocity spectral densities, which the frequencies are twice less the total stiffness frequency of the system (6.50 Hz at n = 2 and 1.92 Hz at n = 3).Subharmonic vibrations at f = 6.50 Hz are clearly visible in Figure 3b and at 1.92 Hz – in Figure 1b. Further research may clarify their origin. For the analyzed dynamic system, the results of which are presented in Figure 3, it was enough to change only the external excitation frequency 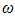 and we obtained a new picture of the system vibration characteristics in Figure 6. This is because the excitation frequency,
and we obtained a new picture of the system vibration characteristics in Figure 6. This is because the excitation frequency, 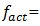 17.84 Hz, is close to the system resonant frequency
17.84 Hz, is close to the system resonant frequency 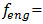 18.38 Hz.
18.38 Hz.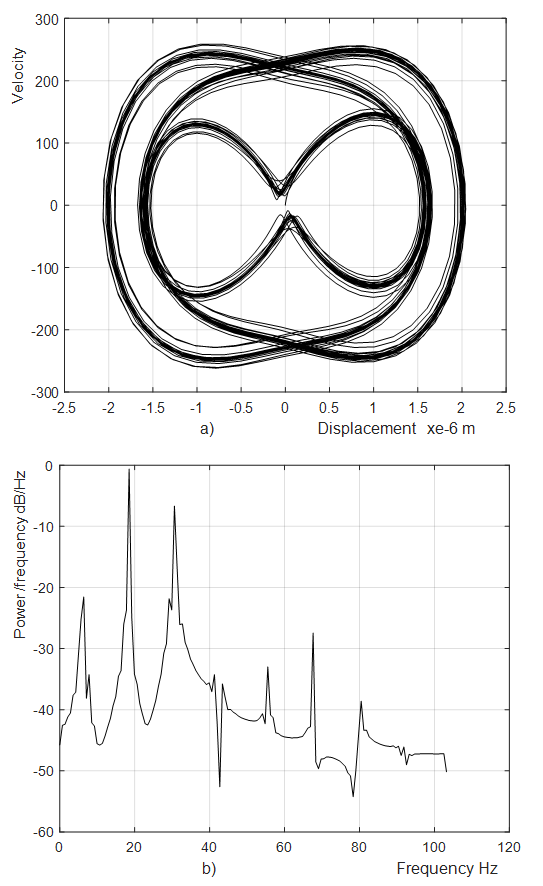 | Figure 6. Results of research for the quadratic nonlinearity of the system when 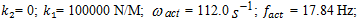 M = 5.0 kg and c = 0.05 M = 5.0 kg and c = 0.05 |
In addition, this excitation frequency also excites the vibration amplitudes of the stiffness resonant frequency 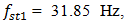 since it is almost twice the excitation frequency and the amplitudes of other frequencies are considerably smaller (Figure 6b). Figure 6b also shows that a large amplitude of vibration is excited at the system total frequency
since it is almost twice the excitation frequency and the amplitudes of other frequencies are considerably smaller (Figure 6b). Figure 6b also shows that a large amplitude of vibration is excited at the system total frequency 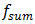 subharmonic frequency, since its frequency is nearly 3 times smaller the external excitation frequency. Without determining resonant and parametric frequencies in a vibrating nonlinear dynamic system, we will not be able to explain the complexity of the phase - space diagrams and the complexity of the vibration process. Moreover, we will not be able to properly determine dynamic system parameters and operating modes. Overall, the results of the studies show that the appropriate parameters and operating modes of the system need to be determined at the design process. Notwithstanding [1-16], no such results have been reported, and neither has there been any analytical determination of nonlinear dynamic relationships between resonant and parametric frequencies and its external excitation frequency. In [15,16] the stability of a simplified (linearized) nonlinear dynamic system of Duffing at (x = 0, ±1) is examined, and also the magnitude of the damping force directly proportional to velocity. However, this does not provide analytical expressions for the system resonant and parametric frequencies and does not comment on it. Moreover, [1-16] do not reveal: force, stiffness and energy relations in the vibrating nonlinear dynamical system and their influence on resonant frequencies. In this way it was impossible to explain the physics of the processes taking place in the vibration nonlinear dynamic system, to create a nonlinear mechanical dynamic system and to determine its safe working conditions, which ensure its lasting and stable operation. The numerical investigation in this research showed that the presented methods for determining the resonant and parametric excitation frequencies are correct, and can be used in the design process for calculating their values for quadratic, cubic and fourth order nonlinearities of the single-degree-of-freedom system.
subharmonic frequency, since its frequency is nearly 3 times smaller the external excitation frequency. Without determining resonant and parametric frequencies in a vibrating nonlinear dynamic system, we will not be able to explain the complexity of the phase - space diagrams and the complexity of the vibration process. Moreover, we will not be able to properly determine dynamic system parameters and operating modes. Overall, the results of the studies show that the appropriate parameters and operating modes of the system need to be determined at the design process. Notwithstanding [1-16], no such results have been reported, and neither has there been any analytical determination of nonlinear dynamic relationships between resonant and parametric frequencies and its external excitation frequency. In [15,16] the stability of a simplified (linearized) nonlinear dynamic system of Duffing at (x = 0, ±1) is examined, and also the magnitude of the damping force directly proportional to velocity. However, this does not provide analytical expressions for the system resonant and parametric frequencies and does not comment on it. Moreover, [1-16] do not reveal: force, stiffness and energy relations in the vibrating nonlinear dynamical system and their influence on resonant frequencies. In this way it was impossible to explain the physics of the processes taking place in the vibration nonlinear dynamic system, to create a nonlinear mechanical dynamic system and to determine its safe working conditions, which ensure its lasting and stable operation. The numerical investigation in this research showed that the presented methods for determining the resonant and parametric excitation frequencies are correct, and can be used in the design process for calculating their values for quadratic, cubic and fourth order nonlinearities of the single-degree-of-freedom system.
5. Conclusions
This paper presents analytical methods for determining the resonant and parametric excitation frequencies of the systems, which enable choosing reasonable dynamic characteristics of the system during the design process for quadratic, cubic and fourth order nonlinearities of single-degree-of-freedom systems and to reduce its vibration level.Analytical resultsThe analytical results indicate that:1. There are four groups of resonant frequencies, determined by the energy, force and stiffness characteristic connections peculiarities and the total stiffness of the nonlinear dynamical system. 2. The nonlinear system generates a very wide spectrum of parametric excitation frequencies and the higher the value of the n parameter the more they will be generated. The frequency of parametric vibration is independent of their amplitude. Parametric excitation frequencies are u times repetitive by the frequency of external excitation.3 When the exponent of polynomial increase then the frequencies determined by the energy characteristic connection peculiarities decrease, while frequencies determined by stiffness connections peculiarities increase. The system's resonant frequencies, which are determined by the energy connection peculiarities, are smaller than the frequencies determined by stiffness connections peculiarities.4. The system's resonant frequencies, which are determined by the force connection peculiarities, are not dependent on the exponent of polynomial. The results of numerical calculationsThe results of numerical calculations allow us to prove that:1. The vibration level of the system significantly increases when the parametric excitation frequency coincides with the system's resonant frequency.2. In the dynamical system, as the values of the parametric frequencies increase, the amplitudes of the vibration decrease significantly.3. By setting the system’s parameters (stiffness, mass, damping, etc.), we determine its resonant frequencies, but the frequency and number of parametric vibrations of a dynamic system depend on the level of nonlinearity of the system.4. The certainty of the analytical methods was verified by numerical calculations.
References
| [1] | Peng Z. K., Lang Z. Q., and Billings S. A, 2006, Resonances and Resonant Frequencies for a Class of Nonlinear Systems. Department of Automatic Control and Systems Engineering. University of Sheffield. Research Report No. 920, p. 30. |
| [2] | A Brief Introduction to Nonlinear Vibrations, 2009, AnIndya Chatterjee Mechanical Engineering, Indian Institute of Science, Bangalore, p. 20. Web: http://home.iitk.ac.in/~anindya/. |
| [3] | Hegazi U. H., Hamato H. F, 2016, Dynamic responses to different excitations of one degree of freedom system with quadratic and cubic nonlinearities. American Journal of Computational and Applied Mathematics, 6(42016), pp. 165-176. |
| [4] | Pratiher B. and Dwivedy S.K, 2008, Non – linear vibration of a single link viscoelastic cartesian manipulator. International Journal Mechanics, pp. 683-696. |
| [5] | Luo J., Liu X, 2015, An approximate response of the large system with local cubic nonlinearities subjected to harmonic excitation. Engineering review, Vol. 35, Issue 1, pp. 49-59. |
| [6] | Fereidoon A., Ghadimi M., Barari A., Kaliji H. D. and Domairry G, 2012, Nonlinear vibration of oscillation systems using frequency – amplitude formulation. Shock and Vibration, 19, pp. 323-332. |
| [7] | Jang H. K, 2005, Design guideline for the improvement of dynamic comfort of a vehicle seat and its application, International Journal of Automotive Technology, 6, pp. 383-390. |
| [8] | Goge D., Sinapius M., Fullekrug U., M. Link M, 2005, Detection and description of non-linear phenomena in experimental modal analysis via linearity plots, International Journal of Non-linear Mechanics, 40, pp. 27-48. |
| [9] | Darpe A.K., Gupta K., Chawla A, 2004, Transient response and breathing behavior of a cracked Jeffcott rotor, Journal of Sound and Vibration, 272, pp. 207-243. |
| [10] | Samuel C., Stanton C., McGeheBrian C., Mann P, 2010, Nonlinear dynamics for broadband energy harvesting: Investigation of a bi stable piezoelectric inertial generator. Physic D: Nonlinear Phenomena, Vol., 239, issue10, pp. 640-653. |
| [11] | Wang. W., Xu, J., Sun, X, 2013, Strong and weak resonances in delayed differential systems. Bifurc. Chaos 23(7), pp. 1-20. |
| [12] | Ji, J. C., Li, X. Y., Zhang. L. Z, 2012, Two–to–one resonant Hopf bifurcation in a quadratically nonlinear oscillator involving time delay. Bifurc. Chaos 22, pp. 1-14. |
| [13] | Luo, J., Liu, X, 2015, An approximate response of the large system with local cubic nonlinearities subjected to harmonic excitation. Engineering Review, 34,1, pp. 49 – 59. |
| [14] | Zhang Y., Pozharskiy D., McFarland D. M., Kevrekidis P.G., Kevrekidis I.G., Vakakis A. F. Experimental study of nonlinear resonances in a forced, ordered granular chain. https://arxiv.org/pdf/1606.093605. Corresponding author yzhng123@illinois.edu. |
| [15] | Tamas Kalmar – Nagy and Balakumar Balachandran, 2011, Forced harmonic vibration of a Duffing oscillator with linear viscous damping. The Duffing Equation: First Edition, Published John Willey and Sons, Ltd, ISBN: 978 – 0 – 470 – 71549, pp. 141-160. |
| [16] | Richard h. Rand, 2005, Lecture Notes on Nonlinear Vibrations. Dept. Theoretical and Applied Mechanics Cornell University, Ithaca NY 14853, rhr2@cornell.edu, p. 111. http://www.tam.cornell.edu/randdors/. |



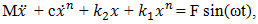
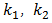 are coefficients of stiffness; n is the exponent of
are coefficients of stiffness; n is the exponent of 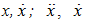 is acceleration and velocity; F is amplitude of external excitement force;
is acceleration and velocity; F is amplitude of external excitement force; 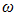 is angular frequency; t is time. It is known that the kinetic energy of the system of motion is equal to its potential energy:
is angular frequency; t is time. It is known that the kinetic energy of the system of motion is equal to its potential energy: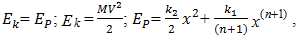
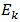 and
and 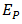 are kinetic and potential energies,
are kinetic and potential energies, 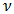 is velocity.With regard to dependence (1), we found that when the amplitude of the vibration becomes equal to one (x = 1), the differential equation of the motion of a nonlinear system (1) becomes linear, because the unit raised in n degrees is equal to one
is velocity.With regard to dependence (1), we found that when the amplitude of the vibration becomes equal to one (x = 1), the differential equation of the motion of a nonlinear system (1) becomes linear, because the unit raised in n degrees is equal to one 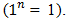 Accordingly, the equation (1), where the value of x is equal to or very close to one, will be expressed as follows:
Accordingly, the equation (1), where the value of x is equal to or very close to one, will be expressed as follows: 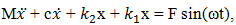
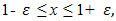 where
where 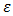 magnitude is small enough.Using the method of solving the linear differential equations of non-damped systems we obtained:
magnitude is small enough.Using the method of solving the linear differential equations of non-damped systems we obtained: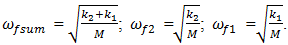
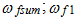 and
and 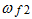 ) in the system caused by force connection peculiarities. After considering the system linearity, we will form an additional equation for the description of the motion of that system using its stiffness characteristics
) in the system caused by force connection peculiarities. After considering the system linearity, we will form an additional equation for the description of the motion of that system using its stiffness characteristics 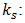
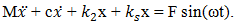
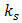 is determined as follows:
is determined as follows: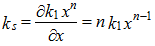 and when x =1 then
and when x =1 then 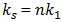 . Equation (5) helped to determine the three resonant system’s frequencies caused by peculiarities of the stiffness connections of the system:
. Equation (5) helped to determine the three resonant system’s frequencies caused by peculiarities of the stiffness connections of the system: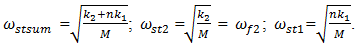
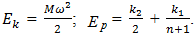 Using the kinetic and potential energy equality condition we then obtain:
Using the kinetic and potential energy equality condition we then obtain: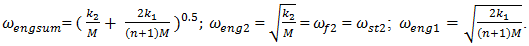
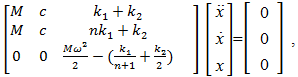
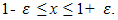 If the dynamic system has energy, force and stiffness connection peculiarities, then the total stiffness of the system will also be the magnitude, which will be evaluated as follows:
If the dynamic system has energy, force and stiffness connection peculiarities, then the total stiffness of the system will also be the magnitude, which will be evaluated as follows: 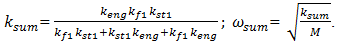
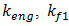 and
and  are coefficient of stiffness, caused by energy, force and stiffness connection peculiarities.Expression (9) is only valid when
are coefficient of stiffness, caused by energy, force and stiffness connection peculiarities.Expression (9) is only valid when 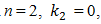 and when n = 2 or n > 2 and
and when n = 2 or n > 2 and 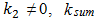 expression are complex and therefore are not included in this article. However, the total stiffness of the system shall in all cases be determined in the same way as for n = 2 and
expression are complex and therefore are not included in this article. However, the total stiffness of the system shall in all cases be determined in the same way as for n = 2 and 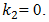 The investigation showed that there are four types of resonant frequency groups in the systems under consideration, which are caused by energy, force, stiffness connections peculiarities and by system total stiffness. Thus, there are 8 different frequencies
The investigation showed that there are four types of resonant frequency groups in the systems under consideration, which are caused by energy, force, stiffness connections peculiarities and by system total stiffness. Thus, there are 8 different frequencies 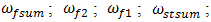
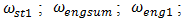
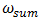 in systems. When
in systems. When 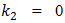 then only four resonant frequencies:
then only four resonant frequencies: 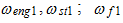 and
and 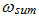 will be in the system. From expressions (4), (6-7) and (9) we observe that the resonant frequency is considerably lower than other ones which are defined by energy, power and stiffness connection peculiarities. Let us consider frequencies ratio:
will be in the system. From expressions (4), (6-7) and (9) we observe that the resonant frequency is considerably lower than other ones which are defined by energy, power and stiffness connection peculiarities. Let us consider frequencies ratio: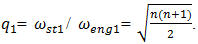
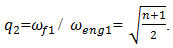
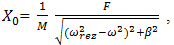
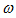 is angular frequency of external excitation force;
is angular frequency of external excitation force; 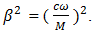 A common case
A common case 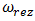 value is calculated according to expression
value is calculated according to expression 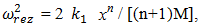 or
or 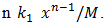
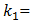 100000 N/m;
100000 N/m; 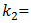 0.0; F = 100000 N; M = 5.0 kg and c = 0.05, were calculated using formulas (4-6), (7,9). The following results were obtained:
0.0; F = 100000 N; M = 5.0 kg and c = 0.05, were calculated using formulas (4-6), (7,9). The following results were obtained: 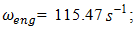
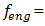
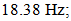
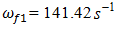
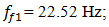
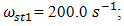
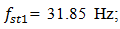
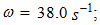
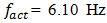 and
and 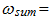
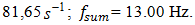
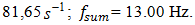 Figure 1b shows that the first peak of the highest intensity is an external acting force
Figure 1b shows that the first peak of the highest intensity is an external acting force 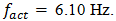 The second peak f = 18.39 Hz corresponds to the frequency generated by the energy connection peculiarities. In this case, the peak of spectral density described with force connections peculiarities
The second peak f = 18.39 Hz corresponds to the frequency generated by the energy connection peculiarities. In this case, the peak of spectral density described with force connections peculiarities 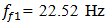 is smaller because of intensive vibration on the resonant frequencies,
is smaller because of intensive vibration on the resonant frequencies, 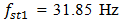 and
and 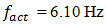 of the system. The very significant increase in the system vibration level at the excitation frequency
of the system. The very significant increase in the system vibration level at the excitation frequency 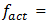
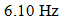 can be explained by the fact that the latter frequency almost coincides with the system frequency of total stiffness subharmonic frequency
can be explained by the fact that the latter frequency almost coincides with the system frequency of total stiffness subharmonic frequency 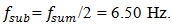 At spectral density in Figure 1b has a maximum vibration level at
At spectral density in Figure 1b has a maximum vibration level at 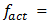
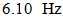 and
and 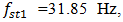 so in Figure 1a, only the vibration waves of
so in Figure 1a, only the vibration waves of 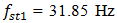 are visible on the low frequency curve
are visible on the low frequency curve 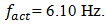 However, at spectral density (Figure 1b) still has lower intensity frequencies at 30;43 and other frequencies and they are not peaks of resonant frequencies. To clarify the nature of the abovementioned frequencies, let us consider the frequencies of parametric vibration in nonlinear dynamical system.
However, at spectral density (Figure 1b) still has lower intensity frequencies at 30;43 and other frequencies and they are not peaks of resonant frequencies. To clarify the nature of the abovementioned frequencies, let us consider the frequencies of parametric vibration in nonlinear dynamical system.
 Hz; F = 100000 N; M = 5.0 kg and c= 0.5
Hz; F = 100000 N; M = 5.0 kg and c= 0.5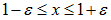 (and only then) that (12) dependency will be valid. Otherwise, it is not possible so simple to express the nonlinear dynamical system vibration dependence on its parameters. However, the latter expression shows that as the amplitude of the vibration increases (when x > 1), the denominator should increase and the amplitude of the vibration than should decrease. Thus, to some degree the nonlinear dynamic system should dampen its vibrations. Moreover, due to its nonlinearity, the vibrating system can generate additional frequency which is called parametric vibration frequencies. To determine these let us consider changes in the velocity and acceleration of stiffness, damping, and inertia forces of nonlinear dynamic system under the influence of the external excitation force F(t) = F sin(ωt).Let us suppose that the aforementioned force will excite vibrations x(t) = A sin (ωt).The dynamic system (1) under consideration contains 4 different types of forces: external excitation, stiffness, damping, and inertia. When n = 1, the forces mentioned above will be such expressions:
(and only then) that (12) dependency will be valid. Otherwise, it is not possible so simple to express the nonlinear dynamical system vibration dependence on its parameters. However, the latter expression shows that as the amplitude of the vibration increases (when x > 1), the denominator should increase and the amplitude of the vibration than should decrease. Thus, to some degree the nonlinear dynamic system should dampen its vibrations. Moreover, due to its nonlinearity, the vibrating system can generate additional frequency which is called parametric vibration frequencies. To determine these let us consider changes in the velocity and acceleration of stiffness, damping, and inertia forces of nonlinear dynamic system under the influence of the external excitation force F(t) = F sin(ωt).Let us suppose that the aforementioned force will excite vibrations x(t) = A sin (ωt).The dynamic system (1) under consideration contains 4 different types of forces: external excitation, stiffness, damping, and inertia. When n = 1, the forces mentioned above will be such expressions: 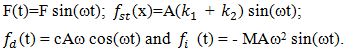
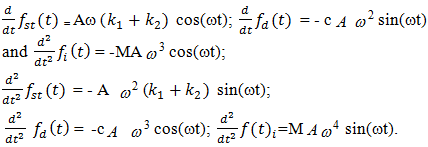
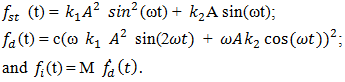
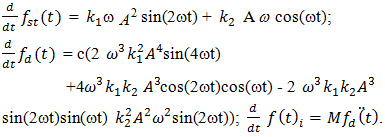
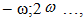 damping force
damping force 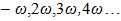 What the frequencies generated by the forces under consideration are shown in (Table 1). In this way, when n = 2, the system will generate parametric vibration with frequency:
What the frequencies generated by the forces under consideration are shown in (Table 1). In this way, when n = 2, the system will generate parametric vibration with frequency: 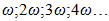 or the parametric frequencies generated in the system can be described as follows:
or the parametric frequencies generated in the system can be described as follows: 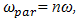 when u = 1;2;3;4… When n = 3, using the above method we get that
when u = 1;2;3;4… When n = 3, using the above method we get that 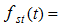
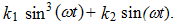 The latter expression shows that stiffness force will generate
The latter expression shows that stiffness force will generate 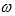 and
and 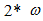 parametric frequencies in the dynamic system. Damping force and their velocity generous
parametric frequencies in the dynamic system. Damping force and their velocity generous 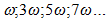 parametric frequencies (Figure 2a). So when the n = 3 parameter u gets the following values: u = 1;3;5;7... When n = 4, the damping force spectrum is shown in Figure 2b.
parametric frequencies (Figure 2a). So when the n = 3 parameter u gets the following values: u = 1;3;5;7... When n = 4, the damping force spectrum is shown in Figure 2b.
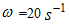 with frequencies, whose value is determined by (17)
with frequencies, whose value is determined by (17)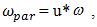
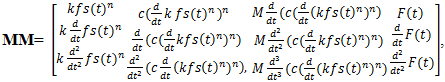
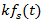 – is the conditional notation of the cumulative effect of the stiffness force on the dynamic system.The analysis of (13-16,17) the dependencies, as well as the data in Table 1 and Figure 2 shows that:when dynamic system n = 1, it does not generate additional frequency parametric vibration;when dynamic systems n >1, it generates parametric vibration of additional frequencies and the higher the value of the n parameter the more they will be generated; in the dynamical system, as the values of the parametric frequencies increase, the amplitudes of the vibration decrease significantly (Figure 2);the results of the study showed that the frequency of parametric vibration is independent of their amplitude; their number and magnitude depend on the parameters of the nonlinearity of the dynamic system;the generated parametric vibration frequencies in a nonlinear dynamical system can be estimated (evaluated) by members of first row of the matrix–table MM. Thus, these studies demonstrate that the nonlinear dynamic system has resonant and parametric vibration frequencies, and identified analytical ways to determine them.
– is the conditional notation of the cumulative effect of the stiffness force on the dynamic system.The analysis of (13-16,17) the dependencies, as well as the data in Table 1 and Figure 2 shows that:when dynamic system n = 1, it does not generate additional frequency parametric vibration;when dynamic systems n >1, it generates parametric vibration of additional frequencies and the higher the value of the n parameter the more they will be generated; in the dynamical system, as the values of the parametric frequencies increase, the amplitudes of the vibration decrease significantly (Figure 2);the results of the study showed that the frequency of parametric vibration is independent of their amplitude; their number and magnitude depend on the parameters of the nonlinearity of the dynamic system;the generated parametric vibration frequencies in a nonlinear dynamical system can be estimated (evaluated) by members of first row of the matrix–table MM. Thus, these studies demonstrate that the nonlinear dynamic system has resonant and parametric vibration frequencies, and identified analytical ways to determine them.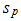 times higher frequency wave (Figure 1a). The value of the
times higher frequency wave (Figure 1a). The value of the 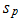 is calculated as follows:
is calculated as follows: 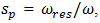
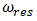 is the system's resonant frequency. Figure 1b clearly shows that the level of the vibration of the resonant frequency
is the system's resonant frequency. Figure 1b clearly shows that the level of the vibration of the resonant frequency 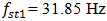 is high enough and sp ratio magnitude for that frequency is approximately (31.85/6.10 = 5.21) 5 times greater than the external excited frequency
is high enough and sp ratio magnitude for that frequency is approximately (31.85/6.10 = 5.21) 5 times greater than the external excited frequency 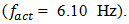 It follows that the wave of resonant vibration (which is defined by stiffness connection peculiarities) will be observed on the wave of the external excitation vibration. In the considering case also
It follows that the wave of resonant vibration (which is defined by stiffness connection peculiarities) will be observed on the wave of the external excitation vibration. In the considering case also 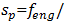
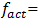 18.39/6.10 = 3.015. It means that the frequency of the
18.39/6.10 = 3.015. It means that the frequency of the 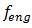 vibration wave on the external excitation vibration wave should repeat approximately 3 times. Yet, the intensity of 18.39 Hz frequency vibration in the spectral density of Figure 1b is significantly lower. When the dynamic system is exciting at the highest resonant frequency
vibration wave on the external excitation vibration wave should repeat approximately 3 times. Yet, the intensity of 18.39 Hz frequency vibration in the spectral density of Figure 1b is significantly lower. When the dynamic system is exciting at the highest resonant frequency 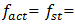 31.85 Hz we get almost concentric ellipses in the phase – space diagram (Figure 3a). It can be seen from the Figure 3b that vibrations of small amplitudes at
31.85 Hz we get almost concentric ellipses in the phase – space diagram (Figure 3a). It can be seen from the Figure 3b that vibrations of small amplitudes at 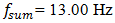 and lower frequencies are excited in the dynamic system. It is important to note that the 13.00 Hz vibration frequency corresponds to the calculated total frequency of the system. The spectral density of the oscillations (Figure 3b) also shows that high intensity parametric vibrations are excited at a frequency of
and lower frequencies are excited in the dynamic system. It is important to note that the 13.00 Hz vibration frequency corresponds to the calculated total frequency of the system. The spectral density of the oscillations (Figure 3b) also shows that high intensity parametric vibrations are excited at a frequency of 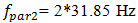 and lower intensity parametric vibration at frequency
and lower intensity parametric vibration at frequency 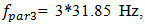
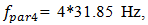 and
and 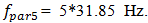 The research showed that at higher excitation forces, the amplitudes of
The research showed that at higher excitation forces, the amplitudes of 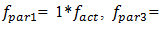
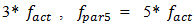 of the parametric vibration frequencies become larger than when the system vibrates at these
of the parametric vibration frequencies become larger than when the system vibrates at these 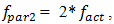
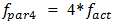
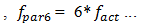 frequencies.
frequencies. 
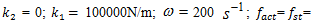 31.85Hz; M = 5.0kg
31.85Hz; M = 5.0kg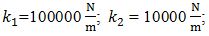 F =100000 N; M = 5.0 kg and c = 0.05, the resonant frequencies of the system were calculated using the formulas (4), (6), (7), (9). The following results were obtained:
F =100000 N; M = 5.0 kg and c = 0.05, the resonant frequencies of the system were calculated using the formulas (4), (6), (7), (9). The following results were obtained: 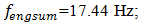
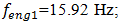
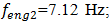
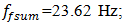
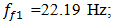
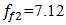
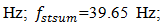
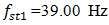 and
and 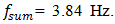 The calculation results of spectral density are shown in Figure 4a. The phase – space diagram in Figure 4b shows that the dynamic system vibrates at a resonant frequency, and that there are approximately
The calculation results of spectral density are shown in Figure 4a. The phase – space diagram in Figure 4b shows that the dynamic system vibrates at a resonant frequency, and that there are approximately 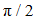 radians between phases of the displacement and velocity and behaves like a linear system.
radians between phases of the displacement and velocity and behaves like a linear system.
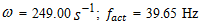 coincides with resonant frequency of the system
coincides with resonant frequency of the system 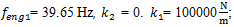 F = 200000 N, M = 5.0 kg
F = 200000 N, M = 5.0 kg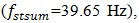 the less significant the second, and the third is determined by the parametric excitation frequencies:
the less significant the second, and the third is determined by the parametric excitation frequencies: 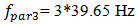 and
and 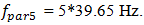 The significant amplitude of the system’s vibration is caused by the external exciting force which frequency coincide with the system resonant frequency
The significant amplitude of the system’s vibration is caused by the external exciting force which frequency coincide with the system resonant frequency 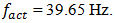 The amplitudes of the lower frequency vibrations are small, because they are invisible in their spectral density Figure 4a.Therefore, the spectral density graph (Figure 4a) shows only the frequencies
The amplitudes of the lower frequency vibrations are small, because they are invisible in their spectral density Figure 4a.Therefore, the spectral density graph (Figure 4a) shows only the frequencies 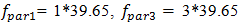 and
and 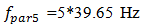 of the parametric vibrations. Thus, the computational results confirm that when n =2;3 and 4, the dynamic system generates the parametric vibration frequencies according to the determined regularities (17). In the case,
of the parametric vibrations. Thus, the computational results confirm that when n =2;3 and 4, the dynamic system generates the parametric vibration frequencies according to the determined regularities (17). In the case, 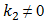 where the external excitation frequency coincides with the system's resonant frequency
where the external excitation frequency coincides with the system's resonant frequency 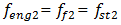 , the resonance conditions in the system will take place when x = 0. The vibration in the system with the cubic nonlinearity at the
, the resonance conditions in the system will take place when x = 0. The vibration in the system with the cubic nonlinearity at the 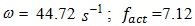
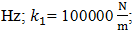
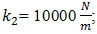 F = 100000 N; M = 5.0 kg and c = 0.05 are shown in Figure 5a and their spectral density – in Figure 5b. By calculating
F = 100000 N; M = 5.0 kg and c = 0.05 are shown in Figure 5a and their spectral density – in Figure 5b. By calculating 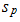 values according the expression (19), we find that
values according the expression (19), we find that 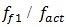 = 22,19/7,12 = 3,12. This means that the frequency defined by the force connection peculiarities is approximately 3 times higher than the external excitation frequency. Hence, in Figure 5a, three higher frequency waves are clearly visible on the low frequency vibration wave. In a spectral density (Figure 5b), we will observe resonant frequencies: 7.12;23.62;39.0 Hz and other parametric frequencies calculated using the analytical method. But when the frequency of the external force coincides with the system's resonant frequency
= 22,19/7,12 = 3,12. This means that the frequency defined by the force connection peculiarities is approximately 3 times higher than the external excitation frequency. Hence, in Figure 5a, three higher frequency waves are clearly visible on the low frequency vibration wave. In a spectral density (Figure 5b), we will observe resonant frequencies: 7.12;23.62;39.0 Hz and other parametric frequencies calculated using the analytical method. But when the frequency of the external force coincides with the system's resonant frequency 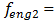 7.12 Hz, then the magnitude of the vibration of that frequency significantly increases and covers smaller amplitudes of vibrations of other frequencies. Therefore, we cannot see vibration of all frequencies of the system in Figure 5a and b.
7.12 Hz, then the magnitude of the vibration of that frequency significantly increases and covers smaller amplitudes of vibrations of other frequencies. Therefore, we cannot see vibration of all frequencies of the system in Figure 5a and b.
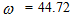
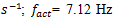
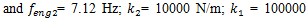
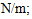 F= 100000 N; M = 5.0 kg
F= 100000 N; M = 5.0 kg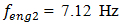 and second, the system parametric excitation frequency
and second, the system parametric excitation frequency 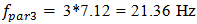 is close to the force connection peculiarities determined frequency
is close to the force connection peculiarities determined frequency 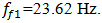 The resonant and parametric excitation frequencies were studied for other parameters of the system, for example:
The resonant and parametric excitation frequencies were studied for other parameters of the system, for example: 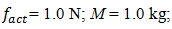
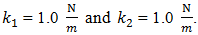 It is important to note that when n = 2;3 and 4 are subharmonics at their vibration and velocity spectral densities, which the frequencies are twice less the total stiffness frequency of the system (6.50 Hz at n = 2 and 1.92 Hz at n = 3).Subharmonic vibrations at f = 6.50 Hz are clearly visible in Figure 3b and at 1.92 Hz – in Figure 1b. Further research may clarify their origin. For the analyzed dynamic system, the results of which are presented in Figure 3, it was enough to change only the external excitation frequency
It is important to note that when n = 2;3 and 4 are subharmonics at their vibration and velocity spectral densities, which the frequencies are twice less the total stiffness frequency of the system (6.50 Hz at n = 2 and 1.92 Hz at n = 3).Subharmonic vibrations at f = 6.50 Hz are clearly visible in Figure 3b and at 1.92 Hz – in Figure 1b. Further research may clarify their origin. For the analyzed dynamic system, the results of which are presented in Figure 3, it was enough to change only the external excitation frequency 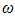 and we obtained a new picture of the system vibration characteristics in Figure 6. This is because the excitation frequency,
and we obtained a new picture of the system vibration characteristics in Figure 6. This is because the excitation frequency, 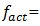 17.84 Hz, is close to the system resonant frequency
17.84 Hz, is close to the system resonant frequency 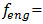 18.38 Hz.
18.38 Hz.
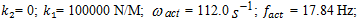 M = 5.0 kg and c = 0.05
M = 5.0 kg and c = 0.05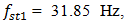 since it is almost twice the excitation frequency and the amplitudes of other frequencies are considerably smaller (Figure 6b). Figure 6b also shows that a large amplitude of vibration is excited at the system total frequency
since it is almost twice the excitation frequency and the amplitudes of other frequencies are considerably smaller (Figure 6b). Figure 6b also shows that a large amplitude of vibration is excited at the system total frequency 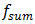 subharmonic frequency, since its frequency is nearly 3 times smaller the external excitation frequency. Without determining resonant and parametric frequencies in a vibrating nonlinear dynamic system, we will not be able to explain the complexity of the phase - space diagrams and the complexity of the vibration process. Moreover, we will not be able to properly determine dynamic system parameters and operating modes. Overall, the results of the studies show that the appropriate parameters and operating modes of the system need to be determined at the design process. Notwithstanding [1-16], no such results have been reported, and neither has there been any analytical determination of nonlinear dynamic relationships between resonant and parametric frequencies and its external excitation frequency. In [15,16] the stability of a simplified (linearized) nonlinear dynamic system of Duffing at (x = 0, ±1) is examined, and also the magnitude of the damping force directly proportional to velocity. However, this does not provide analytical expressions for the system resonant and parametric frequencies and does not comment on it. Moreover, [1-16] do not reveal: force, stiffness and energy relations in the vibrating nonlinear dynamical system and their influence on resonant frequencies. In this way it was impossible to explain the physics of the processes taking place in the vibration nonlinear dynamic system, to create a nonlinear mechanical dynamic system and to determine its safe working conditions, which ensure its lasting and stable operation. The numerical investigation in this research showed that the presented methods for determining the resonant and parametric excitation frequencies are correct, and can be used in the design process for calculating their values for quadratic, cubic and fourth order nonlinearities of the single-degree-of-freedom system.
subharmonic frequency, since its frequency is nearly 3 times smaller the external excitation frequency. Without determining resonant and parametric frequencies in a vibrating nonlinear dynamic system, we will not be able to explain the complexity of the phase - space diagrams and the complexity of the vibration process. Moreover, we will not be able to properly determine dynamic system parameters and operating modes. Overall, the results of the studies show that the appropriate parameters and operating modes of the system need to be determined at the design process. Notwithstanding [1-16], no such results have been reported, and neither has there been any analytical determination of nonlinear dynamic relationships between resonant and parametric frequencies and its external excitation frequency. In [15,16] the stability of a simplified (linearized) nonlinear dynamic system of Duffing at (x = 0, ±1) is examined, and also the magnitude of the damping force directly proportional to velocity. However, this does not provide analytical expressions for the system resonant and parametric frequencies and does not comment on it. Moreover, [1-16] do not reveal: force, stiffness and energy relations in the vibrating nonlinear dynamical system and their influence on resonant frequencies. In this way it was impossible to explain the physics of the processes taking place in the vibration nonlinear dynamic system, to create a nonlinear mechanical dynamic system and to determine its safe working conditions, which ensure its lasting and stable operation. The numerical investigation in this research showed that the presented methods for determining the resonant and parametric excitation frequencies are correct, and can be used in the design process for calculating their values for quadratic, cubic and fourth order nonlinearities of the single-degree-of-freedom system.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML