-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2020; 10(1): 1-5
doi:10.5923/j.ajcam.20201001.01

A Short Survey in Application of Ordinary Differential Equations on Cancer Research
1Department of Life Sciences, Brunel University London, UK
2Department of Mathematics, IAU, Nour Branch, Nour, Iran
Correspondence to: M. Saravi , Department of Mathematics, IAU, Nour Branch, Nour, Iran.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This paper introduces a survey of mathematical models to tumor growth modelling using Ordinary Differential Equations (ODEs) on cancer research. Since the tumor grows voraciously, the scientists and mathematicians have tried to have a better understanding how it grows. Usually, study of such treatments on the models of tumor growth lead to one or more ODEs which gives some ideas on relation between such equations and tumor growth of cancer cells, in particular breast and ovarian cancer cells. In this survey, we introduce some ODEs to provide mathematical models in tumor growth. We emphasis that this paper is useful for the researchers in the field of cancer, hence some objective and new contribution may not clear for the reader. Main goal of this paper is to familiarize reader to applications of ODEs on epidemiology.
Keywords: ODEs, Tumor growth, Tumor volume, Time factor, Gompertzian growth
Cite this paper: S. Saravi , M. Saravi , A Short Survey in Application of Ordinary Differential Equations on Cancer Research, American Journal of Computational and Applied Mathematics , Vol. 10 No. 1, 2020, pp. 1-5. doi: 10.5923/j.ajcam.20201001.01.
1. Introduction
- Knowledge of tumor growth is important in cancer screening planning and treatment. There is strong evidence that tumor growth is directly influenced by the cellular immune system of the human host. An immune system is a collection of biological mechanisms and processes inside an organism with purpose of protecting the organism against diseases and infections. Some mathematical models of a growing tumor and interaction between tumor cells and the host immune system been introduced and many investigations on optimal control treatment strategy on these interactions were done. In this field of study, many researchers applied DEs which arise in many areas of science and technology. Over the past couple of decades DEs have a wide application in the field of medicine. The study of various models of tumour growth and treatment based on ODEs is of interest to many researchers to show how ODEs influence the tumor growth via mathematical models. Most resent one been done [1-5]. Surveys of the literature with numerous references, and useful bibliographies, have been given by these references.A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various order. If differential equation contains a single independent variable, the equation is called Ordinary Differential Equation (ODE). If there is more than one independent variable, the equation is called Partial Differential Equations (PDE). An increasing number of mathematical techniques, using ODEs and PDEs have been applied to various aspects of tumor growth. Many of the spatial models in cancer modelling are based on PDEs that include spatial heterogeneity, orientational tissue structure, tissue stiffness and deformability. Khan [13-14] includes in his review how PDE helps to provide mathematical models of tumor growth. Evolving from the early chemical diffusion and differential equation models of Burton [30] and Greenspan [21], descriptions of tumor growth have been presented more recently using PDEs [25-27]. A PDE model was formulated and studied by Wu et al. [19], which describes the special spread of a replication-component virus within a tumor and its impact on tumor growth. A lot of papers have been devoted to study the nonlinear models [19,15-18]. Explicit models of tumor–virus dynamics using system of PDEs have been discussed, these models are appropriate for tumors that have special structure [24].In this paper we focus on ODEs, because PDEs are more complicated to be discussed here. Simple models of tumor growth and treatment based on a single nonlinear ODEs back to the equation of exponential growth,
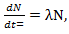 | (1) |
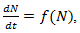 | (2) |
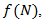 is an appropriate function. A generalization may involve with systems of ODEs. For example, two ODEs are usually needed when considering two cell populations. The models in [11-12] were based on systems of ordinary differential equations.
is an appropriate function. A generalization may involve with systems of ODEs. For example, two ODEs are usually needed when considering two cell populations. The models in [11-12] were based on systems of ordinary differential equations.2. Mathematical Models of Tumor Growth
- In this section we customize a selection (survey) of ODEs related to mathematical modeling of tumor growth. We start with a simple exponential model of tumor growth, where the growth is proportional to the tumor population. This mode of tumor growth expresses the dependence of tumor site on time. This model does not deal with individual cells, but the population of the tumor. The growth of a population as a function of time is considered. Given the population of the tumor, let
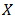 be the number of individual cells at time t. A simple exponential model describes the early stages of tumor growth, where the growth is proportional to the tumor population. If we suppose that the rate of change of the population is proportional to the number of individuals in it at any time we have a differential equation.
be the number of individual cells at time t. A simple exponential model describes the early stages of tumor growth, where the growth is proportional to the tumor population. If we suppose that the rate of change of the population is proportional to the number of individuals in it at any time we have a differential equation. 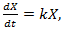 | (3) |
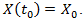 As we mentioned, this model was first applied to cancer growth in 1956 [19]. The population x is positive and increasing due to different biological factors and mutation and so
As we mentioned, this model was first applied to cancer growth in 1956 [19]. The population x is positive and increasing due to different biological factors and mutation and so 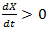 and from Eq. (2) we have k >0. Eq. (2) can easily be solved by separation of variables method. The solution can easily be found and given by
and from Eq. (2) we have k >0. Eq. (2) can easily be solved by separation of variables method. The solution can easily be found and given by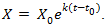 | (4) |
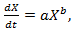 | (5) |
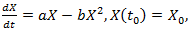 | (6) |
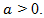 Choose
Choose 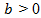 in order to inhibit the growth of x as demanded by reality. This equation is termed as a logistic equation and growth governed by it is called the logistic law of cancer tumor growth. The model represented by this equation is referred to as Verhulst- Pierre model. Eq. (6) also can be solved by separation of variables method. Let
in order to inhibit the growth of x as demanded by reality. This equation is termed as a logistic equation and growth governed by it is called the logistic law of cancer tumor growth. The model represented by this equation is referred to as Verhulst- Pierre model. Eq. (6) also can be solved by separation of variables method. Let 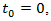 then
then 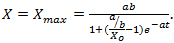 | (7) |
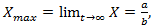 which shows that there is a limit to the growth of
which shows that there is a limit to the growth of 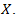 Remark 2.1. The Verhulst equation, of the form
Remark 2.1. The Verhulst equation, of the form 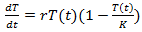 | (8) |
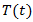 denotes the concentration of tumor cells in a target organism, r is the net reproduction rate of the tumor (which means the difference between proliferation and apoptosis) and K is the carrying capacity.Back to Eq. (3) and consider it for the case of tumor volume
denotes the concentration of tumor cells in a target organism, r is the net reproduction rate of the tumor (which means the difference between proliferation and apoptosis) and K is the carrying capacity.Back to Eq. (3) and consider it for the case of tumor volume 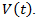 The growth of cancer can be modeled by
The growth of cancer can be modeled by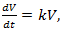 | (9) |
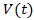 denotes the volume of dividing cells at time t, with an initial volume
denotes the volume of dividing cells at time t, with an initial volume 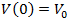 .If the growth is proportional to surface area and that death is proportional to the tumor size then we have Bertalanffy model which is given by (6). It is also known as the surface rule model.
.If the growth is proportional to surface area and that death is proportional to the tumor size then we have Bertalanffy model which is given by (6). It is also known as the surface rule model.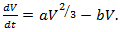 | (10) |
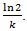 As the tumor becomes larger, the doubling time of the total tumor volume continuously increases. The exponential model predicts early growth well. However, with depletion of nutrients and cell death, exponential growth is not valid for the long-term growth of solid tumors. Thus we investigate several alternative models below. A number of researchers have shown that the data for many solid tumors is fitted remarkably well, over almost a thousand-fold increase in tumor volume, by the equation
As the tumor becomes larger, the doubling time of the total tumor volume continuously increases. The exponential model predicts early growth well. However, with depletion of nutrients and cell death, exponential growth is not valid for the long-term growth of solid tumors. Thus we investigate several alternative models below. A number of researchers have shown that the data for many solid tumors is fitted remarkably well, over almost a thousand-fold increase in tumor volume, by the equation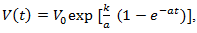 | (11) |
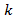 and
and 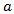 are positive constants. Eq. (11) is usually known as a Gompertzian relation. It states that tumor grows more and more slowly with the passage of time, and that it ultimately approaches the limiting volume
are positive constants. Eq. (11) is usually known as a Gompertzian relation. It states that tumor grows more and more slowly with the passage of time, and that it ultimately approaches the limiting volume 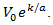 Remark 2.2. The breast cancer growth models proposed by
Remark 2.2. The breast cancer growth models proposed by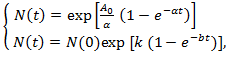 | (12) |
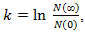 corresponds to classical Gompertzian growth kinetics, where
corresponds to classical Gompertzian growth kinetics, where 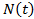 is the number of tumor cells measure at time t after the start of tumor growth,
is the number of tumor cells measure at time t after the start of tumor growth, 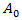 is the initial growth rate, and
is the initial growth rate, and 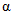 is the rate of growth decay.
is the rate of growth decay. 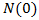 is the tumor starting size, b is the rate of growth decay, and N( ∞ ) is the limiting size [29].The Gompertz model exhibits an exponential decay of the growth rate, given by following nonlinear ODE
is the tumor starting size, b is the rate of growth decay, and N( ∞ ) is the limiting size [29].The Gompertz model exhibits an exponential decay of the growth rate, given by following nonlinear ODE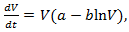 | (13) |
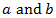 are constants. It has been successfully used to model breast and lung cancer growth. Remark 2.3. The Gompertz equation which been used to model the growth of malignant tumors is given by
are constants. It has been successfully used to model breast and lung cancer growth. Remark 2.3. The Gompertz equation which been used to model the growth of malignant tumors is given by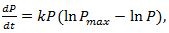 | (14) |
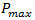 are constants. Let’s back to nonlinear ODE given by (2) and assume
are constants. Let’s back to nonlinear ODE given by (2) and assume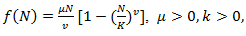 | (15) |
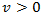 is real and k is the host carrying capacity. For the value
is real and k is the host carrying capacity. For the value 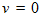 is to be understood as a limit; taking the limit gives the Gompertz equation
is to be understood as a limit; taking the limit gives the Gompertz equation 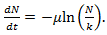 | (16) |
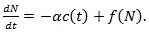 | (17) |
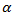 is a positive constant, the strength of the chemotherapeutic agent, and
is a positive constant, the strength of the chemotherapeutic agent, and 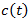 is the agent concentration at the location of the tumor, governed by treatment schedule and pharmacodynamic effects. Since equations (15-17) are nonlinear, hence may not be able to solve them analytically, but they can numerically be solved and their stability and sensitivity, if is necessary, can be described by dynamics of the system because a small change in equation, can produce significant changes in the levels of the tumor cells. In this paper, although equations (13-14) are nonlinear but can easily be solved analytically. Bear in mind that even a linear ODE may be difficult to solve or may not be handled analytically hence computational methods offer. Ovarian cancer is the fifth most common cancer worldwide which is known as “silent killer”. This is the most lethal gynaecologic cancer which after diagnosis, less than 50% of patients can survive more than five years. Unfortunately, the awareness of the risks and symptoms of ovarian cancer between women universally is low. In the other hand, these symptoms can overlap with other signs of common abdominal and gastrointestinal diseases and it is one of the reasons regarding to disease diagnosis at advanced stage in almost 70% of patients. Consequently, many researches been done and released a lot of papers on future screening approaches to help patients at extreme risk of disease, for example [29,32-34]. In the last few decades, lots of mathematicians and scientists have devoted their studies on such disease by using their mathematical modelling on ODEs forms. Kohandel et al. considered one population of tumor cells, a non-cell cycle phase specific drug, and various growth/cell-kill laws in order to compare two approaches for therapy: a) chemotherapy followed by surgery, or b) surgery followed by chemotherapy [32]. Kohandel et al. combined Gompertzian and generalized logistic growth models with different cell-kill hypotheses, and assumed that surgery instantaneously kills a fraction of the tumor cells at the time of the treatment. For both the Gompertzian and generalized growth models, chemotherapy followed by surgery proved to be the optimal approach. They considered one population of tumor cells, a non-cell cycle specific drug and various growth and cell-kill laws formulated in the following manner. The dynamics of the number of tumor cells at time t, N(t), is described by differential functional forms for the growth law by Eq. (15), where f(N) is the tumor cell growth dynamics, G(t,N) describes the effects of the drug on the system , and
is the agent concentration at the location of the tumor, governed by treatment schedule and pharmacodynamic effects. Since equations (15-17) are nonlinear, hence may not be able to solve them analytically, but they can numerically be solved and their stability and sensitivity, if is necessary, can be described by dynamics of the system because a small change in equation, can produce significant changes in the levels of the tumor cells. In this paper, although equations (13-14) are nonlinear but can easily be solved analytically. Bear in mind that even a linear ODE may be difficult to solve or may not be handled analytically hence computational methods offer. Ovarian cancer is the fifth most common cancer worldwide which is known as “silent killer”. This is the most lethal gynaecologic cancer which after diagnosis, less than 50% of patients can survive more than five years. Unfortunately, the awareness of the risks and symptoms of ovarian cancer between women universally is low. In the other hand, these symptoms can overlap with other signs of common abdominal and gastrointestinal diseases and it is one of the reasons regarding to disease diagnosis at advanced stage in almost 70% of patients. Consequently, many researches been done and released a lot of papers on future screening approaches to help patients at extreme risk of disease, for example [29,32-34]. In the last few decades, lots of mathematicians and scientists have devoted their studies on such disease by using their mathematical modelling on ODEs forms. Kohandel et al. considered one population of tumor cells, a non-cell cycle phase specific drug, and various growth/cell-kill laws in order to compare two approaches for therapy: a) chemotherapy followed by surgery, or b) surgery followed by chemotherapy [32]. Kohandel et al. combined Gompertzian and generalized logistic growth models with different cell-kill hypotheses, and assumed that surgery instantaneously kills a fraction of the tumor cells at the time of the treatment. For both the Gompertzian and generalized growth models, chemotherapy followed by surgery proved to be the optimal approach. They considered one population of tumor cells, a non-cell cycle specific drug and various growth and cell-kill laws formulated in the following manner. The dynamics of the number of tumor cells at time t, N(t), is described by differential functional forms for the growth law by Eq. (15), where f(N) is the tumor cell growth dynamics, G(t,N) describes the effects of the drug on the system , and 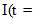
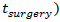 is an indicator function (equal to 1,
is an indicator function (equal to 1, 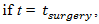 and 0 otherwise). Surgery is assumed to be instantaneous, and to remove a fixed fraction of exp
and 0 otherwise). Surgery is assumed to be instantaneous, and to remove a fixed fraction of exp  of tumor cells, where k s is the fraction of removed cells during surgery.
of tumor cells, where k s is the fraction of removed cells during surgery.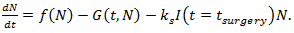 | (18) |
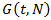 and
and 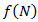 is chosen Eq. (18) can numerically be solved. Many generalizations involve time-evolution analyzed with systems of first-order ODEs. For example, a two-compartment model of angiogenesis and angiogenetic inhibition proposes the following models
is chosen Eq. (18) can numerically be solved. Many generalizations involve time-evolution analyzed with systems of first-order ODEs. For example, a two-compartment model of angiogenesis and angiogenetic inhibition proposes the following models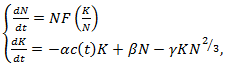 | (19) |
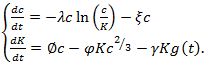 | (20) |
 conceivable as chemotherapy or immunotherapy.To see more system of first order ODEs one may refers to mathematical models of breast and ovarian and prostate cancers [29,35-36].
conceivable as chemotherapy or immunotherapy.To see more system of first order ODEs one may refers to mathematical models of breast and ovarian and prostate cancers [29,35-36].3. Conclusions
- In this review, we introduced several examples of mathematical modelling on cancer research using ODEs since using ODEs to model a biological question requires that there is only one independent variable (such as time) and that all others (such as space) can be neglected. We emphasis that in general, the ODEs and mathematical models can support experimental findings and lead to new avenues of scientific discovery. Although, we did not analysis the models but we put in mind that all models should be analyzed from a qualitative point of view to obtain deeper understanding of the underlying dynamics. In this paper we tried to presented models of ODEs which were not complicated. We observed that, in cases of linear ODEs, usually, they can analytically be solved even we have a system of ODEs. Most of such equations are related to the Gompertz model. We may also encounter with some models which are contained strong nonlinear system, but as we mentioned most of them can numerically be solved and their stability can be analysed by dynamics of the system.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML