| [1] | Simón Martínez-Martínez, Rubén D Leal-Garza, Fausto A Sánchez-Cruz, Esteban Baez Villarreal, and Miguel Amado-Covarrubias. Cfd analysis of the effect of the exhaust manifold design on the close-coupled catalytic converter performance. Journal of KONES, 17:303–311, 2010. |
| [2] | Tao Zhu. Unsteady porous-media flows. PhD thesis, Technische Universität München, 2016. |
| [3] | Vadim S Ermolaev, Kirill O Gryaznov, Eduard B Mitberg, Vladimir Z Mordkovich, and Valentin F Tretyakov. Laboratory and pilot plant fixed-bed reactors for fischer–tropsch synthesis: Mathematical modeling and experimental investigation. Chemical Engineering Science, 138: 1–8, 2015. |
| [4] | A-RA Khaled and K Vafai. The role of porous media in modeling flow and heat transfer in biological tissues. International Journal of Heat and Mass Transfer, 46(26): 4989–5003, 2003. |
| [5] | Adrian Bejan, Ibrahim Dincer, Sylvie Lorente, Antonio Miguel, and Heitor Reis. Porous and complex flow structures in modern technologies. Springer Science & Business Media, 2013. |
| [6] | T Chinyoka and OD Makinde. Analysis of non-newtonian flow with reacting species in a channel filled with a saturated porous medium. Journal of Petroleum Science and Engineering, 121:1–8, 2014. |
| [7] | Zbigniew Żmudka and Stefan Postrzednik. Inverse aspects of the three- way catalytic converter operation in the spark ignition engine. Journal of KONES, 18:509–516, 2011. |
| [8] | Wolfgang Dahmen, Thomas Gotzen, Siegfried Müller, and M Rom. Numerical simulation of transpiration cooling through porous material. International journal for numerical methods in fluids, 76(6): 331–365, 2014. |
| [9] | Jing Fan and Liqiu Wang. Analytical theory of bioheat transport. Journal of Applied Physics, 109(10): 104702, 2011. |
| [10] | Chinedu Nwaigwe. Mathematical modelling of ground temperature with suction velocity and radiation. American Journal of Scientific and Industrial Research, 1(2): 238–241, 2010. |
| [11] | C Israel-Cookey and C Nwaigwe. Unsteady mhd flow of a radiating fluid over a moving heated porous plate with time-dependent suction. American Journal of Scientific and Industrial Research, 1(1): 88–95, 2010. |
| [12] | C Israel-Cookey, E Amos, and C Nwaigwe. Mhd oscillatory couette flow of a radiating viscous fluid in a porous medium with periodic wall temperature. American Journal of Scientific and Industrial Research, 1(2): 326–331, 2010. |
| [13] | R Bhargava, R Sharma, and O. A Beg. Oscillatory chemically-reacting mhd free convection heat and mass transfer in a porous medium with soret and dufour effects - finite element modelling. International Journal of Applied Mathematics and Mechanics, 5(6): 15–37, 2009. |
| [14] | Donald A Nield and Adrian Bejan. Convection in porous media, volume 3. Springer, 2006. |
| [15] | A Mehmood and A Ali. The effect of slip condition on unsteady mhd oscillatory flow of a viscous fluid in a planer channel. Romanian Journal of Physics, 52(1/2):85, 2007. |
| [16] | JA Falade, Joel C Ukaegbu, AC Egere, and Samuel O Adesanya. Mhd oscillatory flow through a porous channel saturated with porous medium. Alexandria engineering journal, 56(1): 147–152, 2017. |
| [17] | R.K. Selvi and R. Muthuraj c. Mhd oscillatory flow of a jeffrey fluid in a vertical porous channel with viscous dissipation. Ain Shams Engineering Journal, 9(4): 2503–2516, 2018. |
| [18] | O. D. Makinde, P. O. Olanrewaju, and W. M. Charles. Unsteady convection with chemical reaction and radiative heat transfer past a flat porous plate moving through a binary mixture. Journal of African Mathematical Union, 22: 65–78, 2011. |
| [19] | Tirivanhu Chinyoka and Daniel Oluwole Makinde. Unsteady and porous media flow of reactive non-newtonian fluids subjected to buoyancy and suction/injection. International Journal of Numerical Methods for Heat & Fluid Flow, 25(7): 1682–1704, 2015. |
| [20] | Chinedu Nwaigwe. Sequential implicit numerical scheme for pollutant and heat transport in a plane-poiseuille flow. Journal of Applied and Computational Mechanics, 6(1): 13–25, 2020. |
| [21] | SM Ibrahim, G Lorenzini, P Vijaya Kumar, and CSK Raju. Influence of chemical reaction and heat source on dissipative mhd mixed convection flow of a casson nanofluid over a nonlinear permeable stretching sheet. International Journal of Heat and Mass Transfer, 111:346–355, 2017. |
| [22] | OD Makinde and PY Mhone. Heat transfer to mhd oscillatory flow in a channel filled with porous medium. Romanian Journal of physics, 50(9/10):931, 2005. |
| [23] | OD Makinde. On steady flow of a reactive variable viscosity fluid in a cylindrical pipe with an isothermal wall. International Journal of Numerical Methods for Heat & Fluid Flow, 17(2): 187–194, 2007. |
| [24] | Gauri Shanker Seth, Rajan Kumar, Rajat Tripathi, and Arnab Bhattacharyya. Double diffusive mhd casson fluid flow in a non-darcy porous medium with newtonian heating and thermo-diffusion effects. International Journal of Heat and Technology, 36(4): 1517–1527, 2018. |
| [25] | Gauri S Seth, Rajat Tripathi, and MM Rashidi. Hydromagnetic natural convection flow in a non-darcy medium with soret and dufour effects past an inclined stretching sheet. Journal of Porous Media, 20(10): 941– 960, 2017. |
| [26] | Chinedu Nwaigwe and Azubuike Weli. Analysis of two finite difference schemes for a channel flow problem. Asian Research Journal of Mathematics, 15:1–14, 2019. |
| [27] | Chinedu Nwaigwe and Charles Orji. Second-order non-oscillatory scheme for simulating a pressure-driven flow. Journal of the Nigerian Association of Mathematical Physics, 52(1): 53–58, 2019. |
| [28] | Fateh Mebarek-oudina and Rachid Bessaïh. Numerical modeling of mhd stability in a cylindrical configuration. Journal of the Franklin Institute, 351(2): 667–681, 2014. |
| [29] | Fateh Mebarek-Oudina and Oluwole Daniel Makinde. Numerical simulation of oscillatory mhd natural convection in cylindrical annulus: Prandtl number effect. In Defect and Diffusion Forum, volume 387, pages 417–427. Trans Tech Publ, 2018. |
| [30] | Jawad Reza, Fateh Mebarek-Oudina, and Oluwole Daniel Makinde. Mhd slip flow of cu-kerosene nanofluid in a channel with stretching walls using 3-stage lobatto iiia formula. In Defect and Diffusion Forum, volume 387, pages 51–62. Trans Tech Publ, 2018. |
| [31] | Fateh Mebarek-Oudina. Numerical modeling of the hydrodynamic stability in vertical annulus with heat source of different lengths. Engineering science and technology, an international journal, 20(4): 1324–1333, 2017. |
| [32] | Salim Hamrelaine, Fateh Mebarek-Oudina, and Mohamed Rafik Sari. Analysis of mhd jeffery hamel flow with suction/injection by homotopy analysis method. J. Adv. Res. Fluid Mech. Therm. Sci, 58:173–186, 2019. |
| [33] | Fateh Mebarek-Oudina. Convective heat transfer of titania nanofluids of different base fluids in cylindrical annulus with discrete heat source. Heat TransferAsian Research, 48(1): 135–147, 2019. |
| [34] | Oluwole D Makinde and T Chinyoka. Numerical investigation of transient heat transfer to hydromagnetic channel flow with radiative heat and convective cooling. Communications in Nonlinear Science and Numerical Simulation, 15(12): 3919–3930, 2010. |
| [35] | T Chinyoka and Oluwole D Makinde. Computational dynamics of unsteady flow of a variable viscosity reactive fluid in a porous pipe. Mechanics Research Communications, 37(3): 347–353, 2010. |
| [36] | E Kumaresan, AG Vijaya Kumar, and J Prakash. Exact solution of unsteady mhd free convective chemically reacting visco-elastic fluid flow past a moving vertical plate through porous medium. International Journal of Applied and Computational Mathematics, 3(4): 3897–3923, 2017. |
| [37] | KV Prasad, K Vajravelu, Hanumesh Vaidya, MM Rashidi, and Z Basha Neelufer. Flow and heat transfer of a casson liquid over a vertical stretching surface: Optimal solution. American Journal of Heat and Mass Transfer, 5(1): 1–22, 2018. |
| [38] | O Anwar Bég and Oluwole D Makinde. Viscoelastic flow and species transfer in a darcian high-permeability channel. Journal of Petroleum Science and Engineering, 76(3-4): 93–99, 2011. |
| [39] | Ram Prakash Sharma, M.C. Raju, O.D. Makinde, P.R. Krishna Reddy, and P. Chandra Reddy. Buoyancy effects on unsteady mhd chemically reacting and rotating fluid flow past a plate in a porous medium. Defect and Diffusion Forum, 392: 1–9, 2018. |
| [40] | Aleksandr Andreevich Samarskii. The theory of difference schemes. New York: Marcel Dekker, 2001. |
| [41] | Piotr Matus, Lubin G Vulkov, et al. Analysis of second order difference schemes on non-uniform grids for quasilinear parabolic equations. Journal of Computational and Applied Mathematics, 310: 186–199, 2017. |


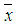 and
and 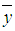 axis are as indicated in the figure. We then consider a flow strictly along the channel axis, fully developed and driven by constant pressure gradient and gravitational and magnetic body forces. The two channel walls are immovable and the fluid is incompressible with temperature-dependent viscosity. A uniform magnetic field is applied perpendicular to the walls and viscous dissipation is incorporated.
axis are as indicated in the figure. We then consider a flow strictly along the channel axis, fully developed and driven by constant pressure gradient and gravitational and magnetic body forces. The two channel walls are immovable and the fluid is incompressible with temperature-dependent viscosity. A uniform magnetic field is applied perpendicular to the walls and viscous dissipation is incorporated.
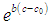 per unit volume of the fluid, where
per unit volume of the fluid, where 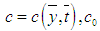 and b are, respectively, the substance’s concentration at point
and b are, respectively, the substance’s concentration at point 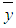 and at time,
and at time, 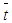 ; a reference concentration; and a constant. We also incorporate cross-diffusion effects, meaning that combined temperature variations due to mass diffusion and concentration variations due to heat diffusion - the Soret-Dufour effects. Bousinesq’s approximation is adopted for the fluid body forces due to solutal and thermal variations.On the channel wall boundaries, the no-slip condition apply, and the temperature and concentration are kept constant at Tw and cw respectively. At initial time, the fluid velocity has a parabolic profile with maximum value at the channel center and vanishes at the walls in line with the no-slip conditions. Both the temperature and concentration are initially zero within the fluid except at the walls where the constant values are maintained.Denoting by
; a reference concentration; and a constant. We also incorporate cross-diffusion effects, meaning that combined temperature variations due to mass diffusion and concentration variations due to heat diffusion - the Soret-Dufour effects. Bousinesq’s approximation is adopted for the fluid body forces due to solutal and thermal variations.On the channel wall boundaries, the no-slip condition apply, and the temperature and concentration are kept constant at Tw and cw respectively. At initial time, the fluid velocity has a parabolic profile with maximum value at the channel center and vanishes at the walls in line with the no-slip conditions. Both the temperature and concentration are initially zero within the fluid except at the walls where the constant values are maintained.Denoting by 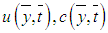 and
and 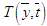 the velocity, concentration and temperature, respectively, at point
the velocity, concentration and temperature, respectively, at point 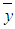 and time
and time 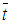 ; and defining
; and defining 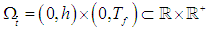 . Then, the problem is governed by the following system [18,6,19,20]:
. Then, the problem is governed by the following system [18,6,19,20]: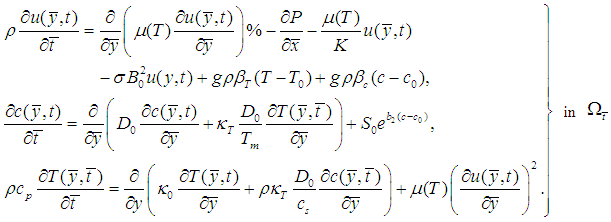
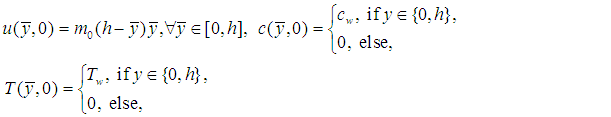
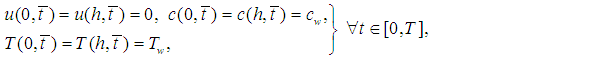
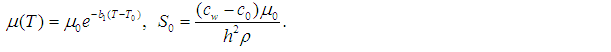
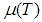 = temperature-dependent fluid viscosity, P = fluid pressure, K = permeability of porous medium, σ = electrical conductivity, B0 = uniform magnetic field intensity, g = acceleration due to gravity, βT = temperature expansion coefficient, βC = concentration expansion coefficient, T0 = reference temperature, D0 = diffusion coefficient,
= temperature-dependent fluid viscosity, P = fluid pressure, K = permeability of porous medium, σ = electrical conductivity, B0 = uniform magnetic field intensity, g = acceleration due to gravity, βT = temperature expansion coefficient, βC = concentration expansion coefficient, T0 = reference temperature, D0 = diffusion coefficient, 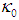 = thermal conductivity,
= thermal conductivity, 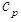 = specific heat capacity,
= specific heat capacity, 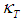 = thermal diffusion ratio, m0 = a constant, Tm = mean fluid temperature,
= thermal diffusion ratio, m0 = a constant, Tm = mean fluid temperature, 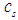 = the concentration susceptibility, while b1 and b2 are constants.
= the concentration susceptibility, while b1 and b2 are constants.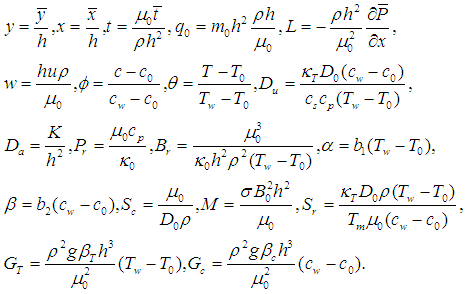
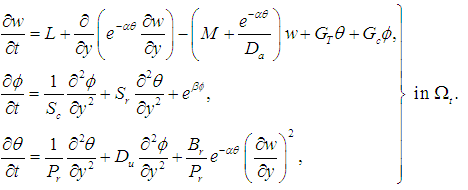
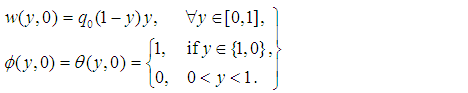
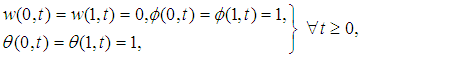
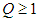 be an integer and
be an integer and 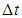 be given. Define
be given. Define 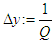 ;
; 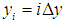 for
for 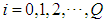 ;
; 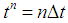 for
for 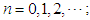 and
and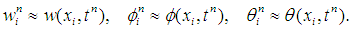 Also, define
Also, define 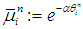 , and
, and 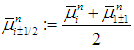 . We propose to discretize the coupling and nonlinear source terms explicitly, while the variable-coefficient viscous terms are treated in conservative form. This leads to the following semi-implicit scheme [40,41] see also [20]:
. We propose to discretize the coupling and nonlinear source terms explicitly, while the variable-coefficient viscous terms are treated in conservative form. This leads to the following semi-implicit scheme [40,41] see also [20]: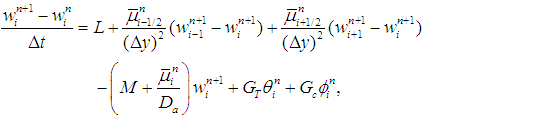
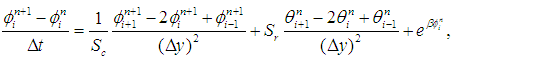
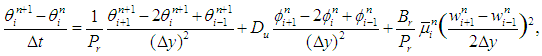
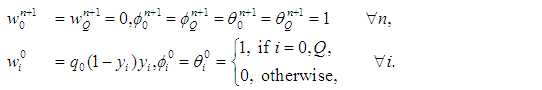
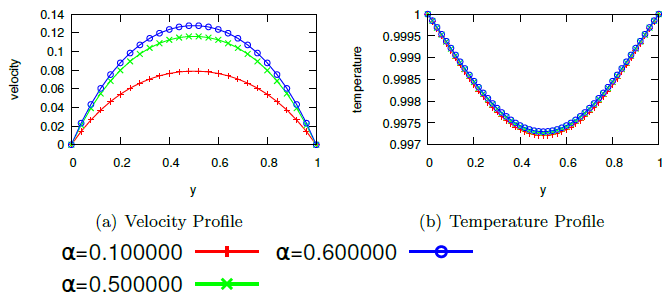
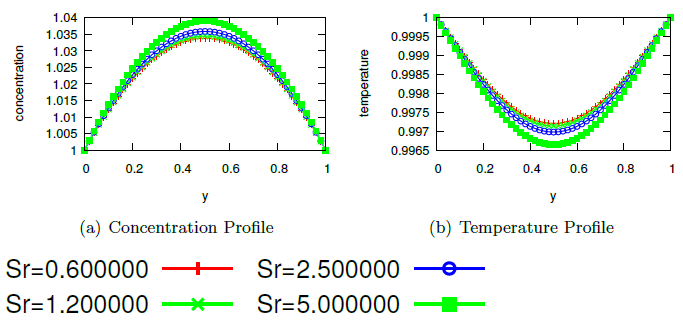
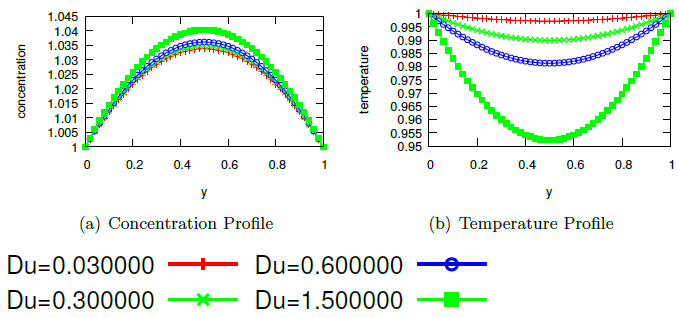
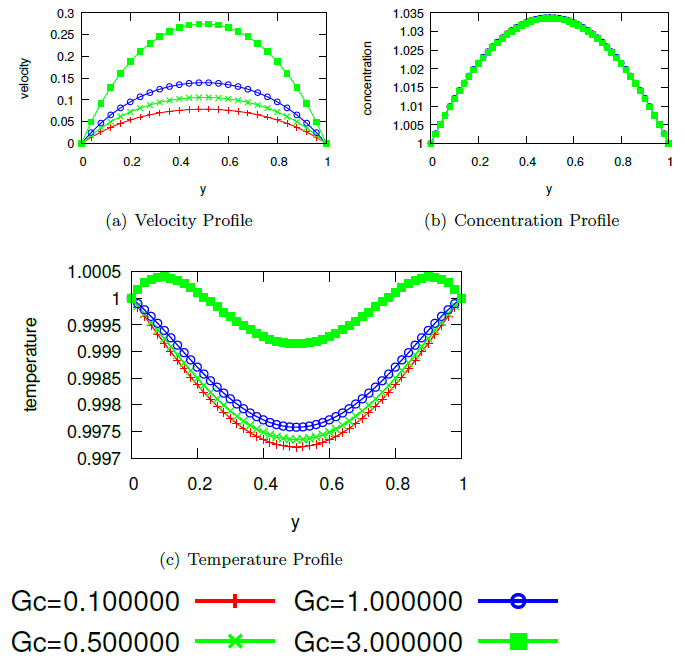
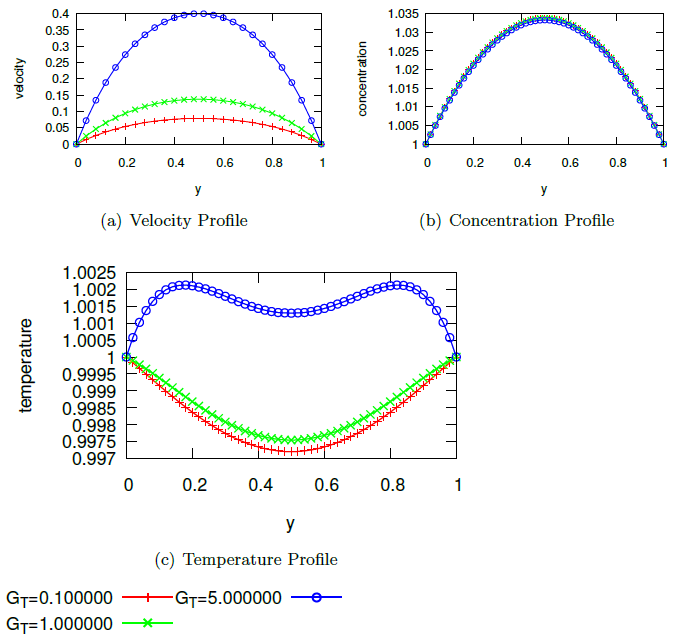
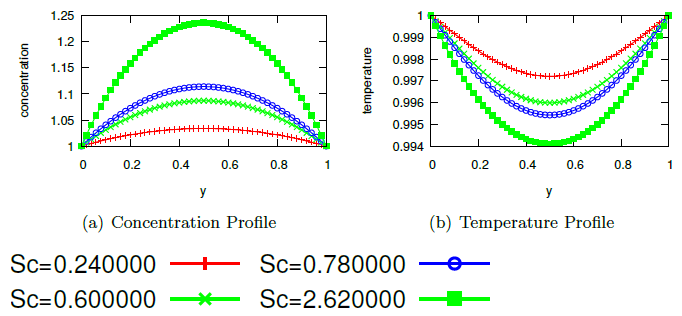
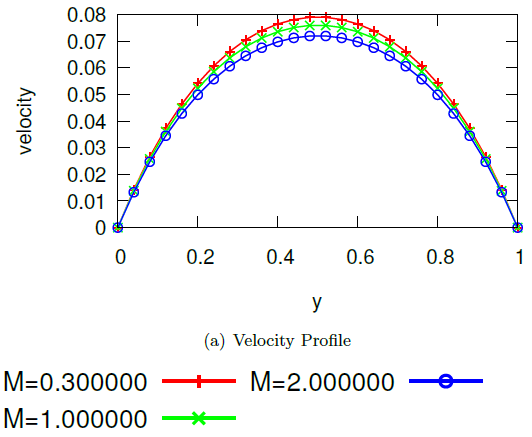
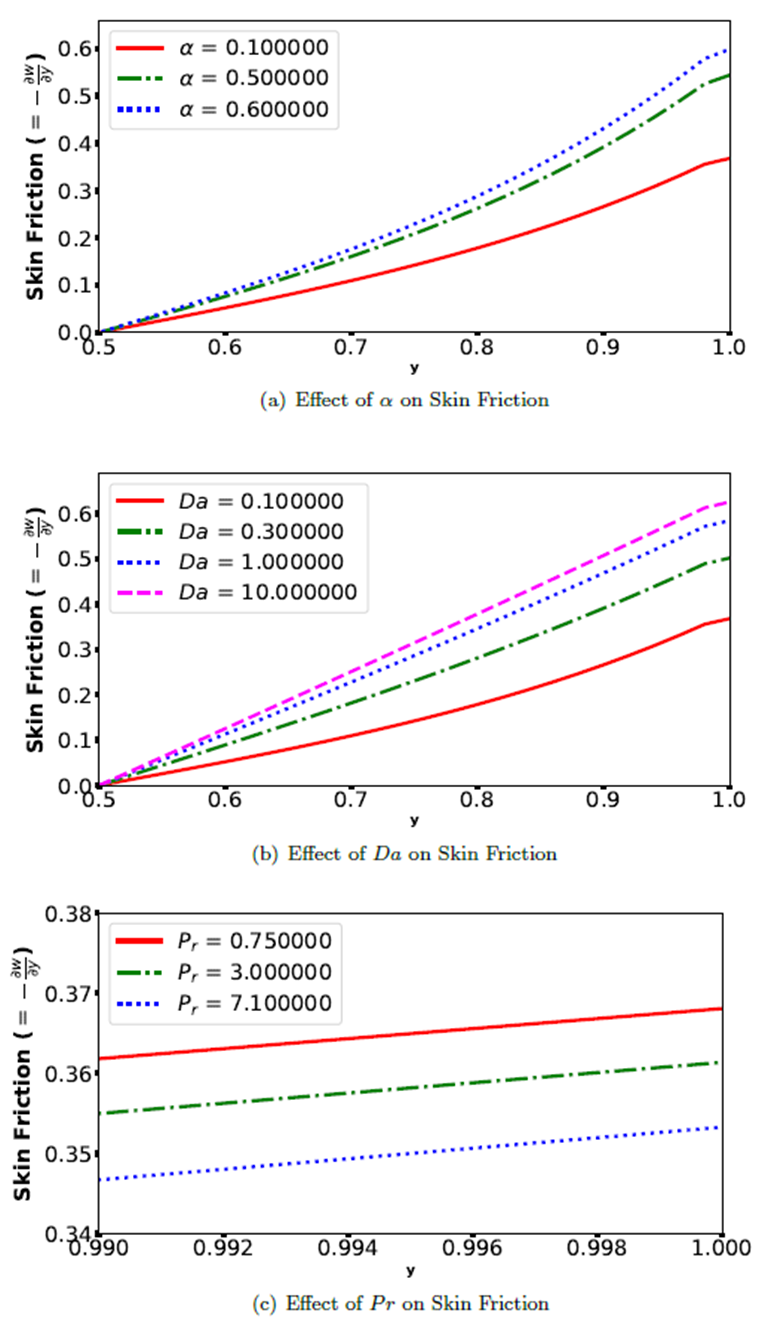
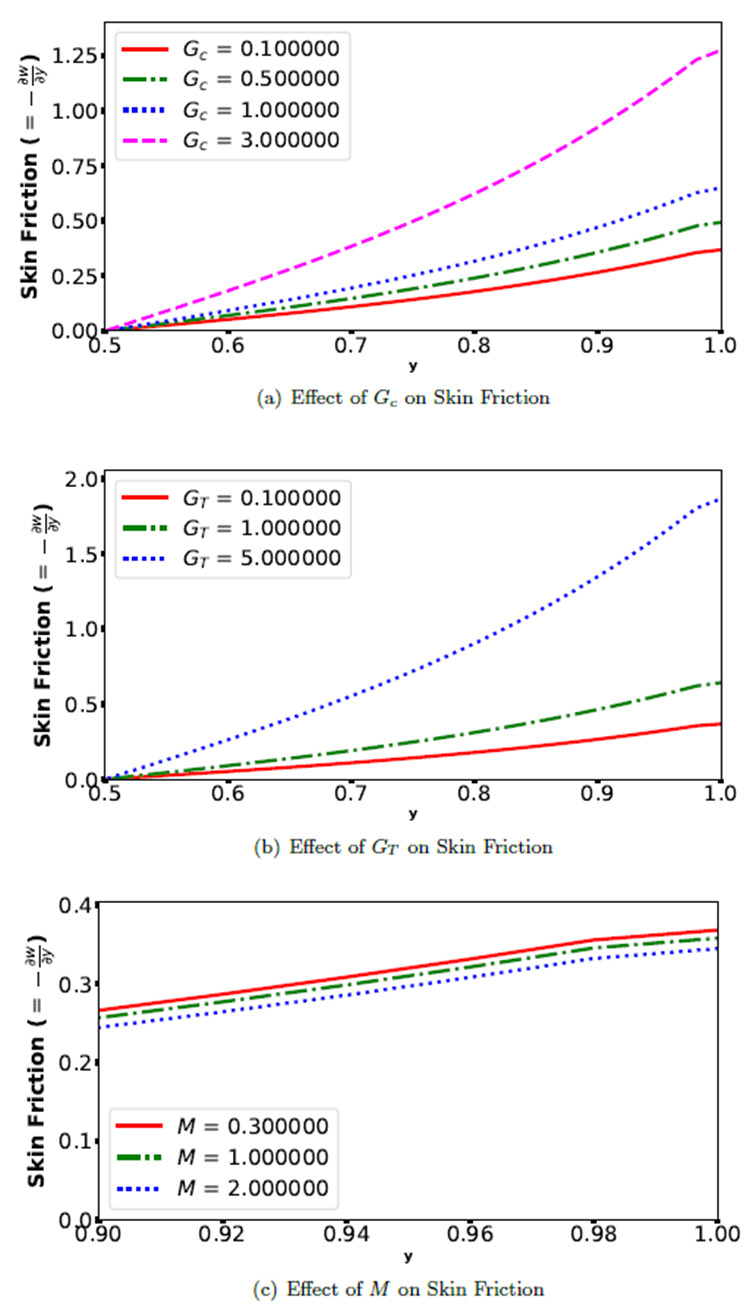
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML