-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2019; 9(4): 110-118
doi:10.5923/j.ajcam.20190904.03

A Special Case of Symmetric Matrices and Their Applications
Ognyan Ivanov Zhelezov
Part-time lecturer, Nikola Vaptsarov Naval Academy, Varna, Bulgaria
Correspondence to: Ognyan Ivanov Zhelezov, Part-time lecturer, Nikola Vaptsarov Naval Academy, Varna, Bulgaria.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This article presents a special case of symmetric matrices, matrices of transpositions (Tr matrices) that are created from the elements of given n-dimensional vector X∈Rn, n=2m, m∈N. Has been proposed algorithm for obtaining matrices of transpositions with mutually orthogonal rows (Trs matrices) of dimensions 2, 4, and 8 as Hadamard product of Tr matrix and matrix of Hadamard and has been investigated their application for QR decomposition and n-dimensional rotation matrix generation. Tests and analysis of the algorithm show that obtaining an orthogonal Trs matrix of sizes 4 and 8 that rotates a given vector to the direction of one of the coordinate axes requires less processing time than obtaining a Housholder matrix of the same size.
Keywords: Mathematics of computing, Mathematical analysis, Numerical analysis, Computations on matrices
Cite this paper: Ognyan Ivanov Zhelezov, A Special Case of Symmetric Matrices and Their Applications, American Journal of Computational and Applied Mathematics , Vol. 9 No. 4, 2019, pp. 110-118. doi: 10.5923/j.ajcam.20190904.03.
Article Outline
1. Introduction
- This article presents a special case of symmetric matrices, matrices of transpositions (Tr matrices) that are created from the elements of given n-dimensional vector X∈Rn, n=2m, m∈N, where value of every matrix’s element is equal to this element of vector X, which index is equal to bitwise XOR of zero based row and column indices of matrix’s element. It has been proved that elements of every two rows makes n/2 fours of elements, in which elements, having different row and column indices (we name them “diagonal elements”) consists the value of the same element of the given vector X. It has been defined type of matrices of transpositions (Trs matrices) having are mutually orthogonal rows, as Hadamard product of Tr matrix and n-dimensional Hadamard matrix having defined ordering of rows against Sylvester-Hadamard matrix. Has been investigated the application of Trs matrix for QR decomposition and n-dimensional rotation matrix generation.
2. Definition of Tr Matrix & Notations
- Matrix of Transpositions (Tr matrix) is square matrix with dimension n=2m, m∈N, which rows are permutations of elements Xk, k∈[0, n-1] of given n-dimensional vector X and the values of elements Trp,q of matrix are obtained from the elements of given vector as follows:
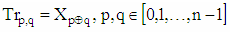 | (1) |
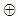 denotes operation „bitwise exclusive or“ (XOR) [22], [23].When it is needed to denote from which vector have been obtained the values of Tr matrix’s elements, we will use for the Tr matrix denotation Tr(X), and for its elements - denotation Tr(X)p,q.As it given in (1), we will use zero based indices for vector’s elements and for Tr matrix’s rows and columns: p,q = 0,1,…,n-1.As it can be seen from the definition of the matrix, it contains only the values of the elements of a given vector. What sets it apart from other similar matrices is the “property of the fours”, which is described belowThe figure, given below shows 8-dimensional Tr matrix, created from arbitrary vector X=(x0,x1, … x7)T.
denotes operation „bitwise exclusive or“ (XOR) [22], [23].When it is needed to denote from which vector have been obtained the values of Tr matrix’s elements, we will use for the Tr matrix denotation Tr(X), and for its elements - denotation Tr(X)p,q.As it given in (1), we will use zero based indices for vector’s elements and for Tr matrix’s rows and columns: p,q = 0,1,…,n-1.As it can be seen from the definition of the matrix, it contains only the values of the elements of a given vector. What sets it apart from other similar matrices is the “property of the fours”, which is described belowThe figure, given below shows 8-dimensional Tr matrix, created from arbitrary vector X=(x0,x1, … x7)T. | Figure 1. 8-dimensional Tr matrix created from vector X=(x0,x1, … x7)T |
 | Example 1. Matlab function, which creates and returns Tr matrix obtained from given n-dimensional vector X, n=2m, m∈N |
3. Properties of Tr matrices
- Properties of Tr matrices in most of cases are determined by the properties of bitwise XOR operation which relates indices of given vector X and indices of matrix’s elements, as it is given in (1). Below are listed and proved some of them, which we consider as most fundamental.
3.1. Tr matrix is symmetric matrix
- This property follows from commutativity of bitwise XOR operation
 From definition of Tr matrix we have
From definition of Tr matrix we have 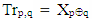 and taking in consideration commutativity of XOR operation we have
and taking in consideration commutativity of XOR operation we have 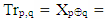
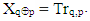 which proves that Tr matrix is symmetric.
which proves that Tr matrix is symmetric.3.2. Every One Row and Column of Tr Matrix Consists all n Elements of Given Vector X without Repetition
- Since Tr matrix’s rows and columns and given vector X have the same dimension, it is enough to prove that every row and column consists elements of given vector X without repetition. To prove that every row of Tr matrix consists elements of given vector X without repetition we will prove that if two elements of the same row Trp,q и Trp,r consists value of the same element of the given vector X, then indices of their columns are equal, i.e. q=r which means that Trp,q and Trp,r denotes the same element of Tr matrix.Proof: Let's examine two arbitrary elements Trp,q and Trp,u of Tr matrix’s row p. Since
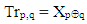 and
and 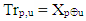 (1) and according to condition above we have
(1) and according to condition above we have 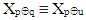 which mean that
which mean that 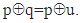 Multiplying two sides of this equation by p, according properties of XOR operation, we get:
Multiplying two sides of this equation by p, according properties of XOR operation, we get: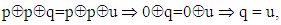 | (2) |
3.3. First Row & First Column of Tr Matrix Consists Elements of Given Vector X in Normal Order (without Inversions)
- This property is determined by the properties of bitwise XOR operation too. If one element Trp,q of Tr matrix belongs to the first row (i.e. p=0), then
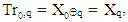 which means that values of elements of first row are equal to the values of elements of given vector X having the same indices, i.e. in normal order. Since Tr is symmetric matrix, the same is valid for first matrix’s column Q.E.D.
which means that values of elements of first row are equal to the values of elements of given vector X having the same indices, i.e. in normal order. Since Tr is symmetric matrix, the same is valid for first matrix’s column Q.E.D.3.4. Property of the Fours
- This property, named “property of the fours” presents relation between four Tr matrix’s elements. It is defined as follows: If two elements of different Tr matrix’s rows are equal to the same element of the given vector X, then the exchange of their column indices gives indices of another two Tr matrix’s elements, that are equal also to the same element of the given vector X (but different from this for the first two). On the scheme of Tr matrix (Figure 2) the fours of elements are located at the vertices of rectangles, such as the diagonal elements of every rectangle contain the same element of the vector X.
 | Figure 2. Example of fours of elements in 8-dimensional Tr matrix, for which it is satisfied Tr-property |
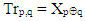 and
and 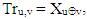 for the indices of which is satisfied equality
for the indices of which is satisfied equality 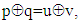 that is they contain the same element
that is they contain the same element 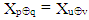 of vector X. We will prove that from this follows that for the elements
of vector X. We will prove that from this follows that for the elements 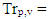
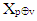 and
and 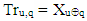 is satisfied equality
is satisfied equality 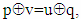 that is they contain the same element
that is they contain the same element 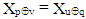 of given vector X too.Proof: Let's look at the equation
of given vector X too.Proof: Let's look at the equation 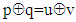 which is satisfied on condition. Multiplying by p to the right of the two sides of the equation, we get:
which is satisfied on condition. Multiplying by p to the right of the two sides of the equation, we get: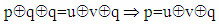 | (3) |
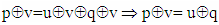 | (4) |
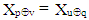 so Trp,v and Tru,q consists the same element of given vector X which proves the property.This property, that we shall hereafter call “Tr-property” is specific to Tr matrix. The figure above shows an example of 8-dimensional Tr matrix in which are indicated by dotted lines several groups of 4 elements, which form rectangles with equal diagonal elements (which mean, that they satisfy Tr-property).
so Trp,v and Tru,q consists the same element of given vector X which proves the property.This property, that we shall hereafter call “Tr-property” is specific to Tr matrix. The figure above shows an example of 8-dimensional Tr matrix in which are indicated by dotted lines several groups of 4 elements, which form rectangles with equal diagonal elements (which mean, that they satisfy Tr-property).3.5. Every Two Rows of Tr Matrix Consists n/2 Fours of Elements with the Same Values of the Diagonal Elements
- Let's look at two arbitrary elements Trp,q and Tru,q from the same column q of two different Tr matrix’s rows p and u, p≠u. According to Tr-property, for those two elements in Tr matrix are contained two corresponding elements Trp,v and Tru,v, for which are satisfied equations Trp,q = Tru,v и Trp,v = Tru,q. Since in each fours of elements two elements are contained in one of the rows and two in the other, to prove that the number of fours is n / 2, it is sufficient to prove that each element of row p is involved in only one fours with elements of row u.Proof: Suppose the element Trp,q of p participates in two fours with elements of row u. This would mean that there are two elements Tru,v and Tru,s in the row u of the Tr matrix, for indices of which are satisfied the equations
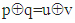 and
and 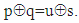 But it would follow, that
But it would follow, that 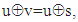 where by multiplying the two sides of equality by u we get v=s, which mean that elements are the same, and therefore the element Trp,q participates in only one fours with elements from row u. Since every one of fours consists two elements of row p, it follows that rows p and u consists n/2 fours of elements, Q.E.D.
where by multiplying the two sides of equality by u we get v=s, which mean that elements are the same, and therefore the element Trp,q participates in only one fours with elements from row u. Since every one of fours consists two elements of row p, it follows that rows p and u consists n/2 fours of elements, Q.E.D. | Figure 3. Fours of elements in 8-dimensional Tr matrix between elements of rows 1-2 and 5-7, for which it is satisfied Tr-property |
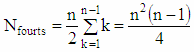 | (5) |
4. Matrix of Transpositions with Mutually Orthogonal Rows
- Matrix of Transpositions with mutually orthogonal rows (Trs matrix) is square matrix with dimension n=2,4 or 8, which is obtained as Hadamard product, (denoted by ○) of Tr matrix and n-dimensional Hadamard matrix whose rows (except the first one) are rearranged relative to the rows of Sylvester-Hadamard matrix in order R=[1, r2, … rn]T, r2, … rn ∈[2,n] for which the rows of the resulting Trs matrix are mutually orthogonal.
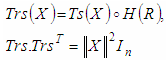 | (6) |
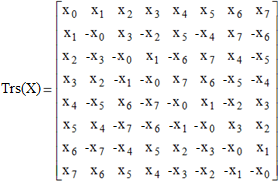 | Figure 4. Schema of 8-dimensional Trs matrix for vector X=[x0,x1, … x7]T |
 | Example 2. Matlab function, that creates and returns a Trs matrix for a given vector X of size n = 2, 4, or 8 |
5. Fours of Elements in the Trs и H(R) Matrices
- We shall hereafter call Trs fours of elements (or just Trs-fours) the elements (Trsp,q, Trsp,v, Trsu,q, Trsu,v) of rows p and u of Trs matrix, where p,q,u,v∈[0,n-1] and p≠u, if their corresponding elements from the Tr matrix (Trp,q, Trp,v, Tru,q, Tru,v) satisfy the Tr-property. As proved in 3.3, to have this, it is necessary for the indices p, q, u, v of the elements to satisfy the equality
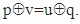 Similarly, we will call H fours of elements (or just H-fours) elements H(R)p,q, H(R)p,v, H(R)u,q, H(R)u,v of rows p and u of H(R) matrix, where p,q,u,v∈[0,n-1] and p≠u, if their corresponding elements from the Tr matrix (Trp,q, Trp,v, Tru,q, Tru,v) satisfy the Tr-property.
Similarly, we will call H fours of elements (or just H-fours) elements H(R)p,q, H(R)p,v, H(R)u,q, H(R)u,v of rows p and u of H(R) matrix, where p,q,u,v∈[0,n-1] and p≠u, if their corresponding elements from the Tr matrix (Trp,q, Trp,v, Tru,q, Tru,v) satisfy the Tr-property.6. Properties of Trs Matrices
- The properties of the Trs matrix are determined by its definition and by the method of its preparation, given in (5).
6.1. The Fours of Elements in the Trs Matrix Form Pairs of Orthogonal Two-Dimensional Vectors – Trs-Property
- The set vector X uniquely defines the Tr matrix, while for the n-dimensional Hadamard matrix H(R)n the definition only requires that the rows of the matrix have to be interchanged relative to the Sylvester-Hadamard matrix for ordering R=[1, r2, … rn]T, so that the rows of the resulting Trs matrix are mutually orthogonal. This mutual orthogonality of the rows of the Trs matrix is obtained when the two-dimensional vectors in the Trs-fours are mutually orthogonal. This property of the Trs-fours (orthogonal pairs of two-dimensional vectors) hereafter we shall call Trs-property. To demonstrate this property, let's look at two rows of the 8-bit Tr matrix from Figure 1 (such as rows 1 and 2) and the result of their Hadamard product by rows from the Hadamard matrix. Rows 1 and 2 of the 8-bit Tr matrix have the following contents:
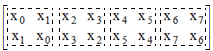 | Figure 5. Schema of the fours of elements in the first two rows of an 8-bit Tr matrix |
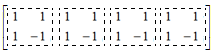 | Figure 6. Schema of the first two rows of Silvester-Hadamard matrix |
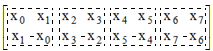 | Figure 7. Schema of the fours of elements in the first two rows of an 8-dimensional Trs matrix |
6.2. The Fours of Elements in the Hadamard H(R) n-dimensional Matrix must Form Pairs of Orthogonal Two-Dimensional Vectors
- We will prove that in order to obtain the orthogonality of the Trs-fours in the Trs matrix (which also implies the mutual orthogonality of the rows), it is sufficient the corresponding H-fours in the n-dimensional matrix of Hadamard H(R)n to contain orthogonal vectors.Let's look at the Trs-fours (Trsp,q, Trsp,v, Trsu,q, Trsu,v), p,q,u,v∈[0,n-1] of rows p and u of Trs matrix. According to the definition of the Trs matrix, they are obtained by element by element multiplication (Hadamard product) of the corresponding elements of the Tr matrix (Trp,q, Trp,v, Tru,q, Tru,v), which satisfy T-property and corresponding elements (H(R)p,q, H(R)p,v, H(R)u,q, H(R)u,v of Hadamard matrix H(R). To be two-dimensional vectors
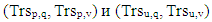 | (7) |
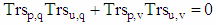 | (8) |
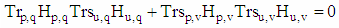 | (9) |
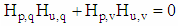 | (10) |
6.3. The Trs Matrix Created by a Unit Vector X is an Orthogonal Matrix
- This property follows from the definition of the Trs matrix (4), according to which the rows of the Trs matrix are mutually orthogonal and contain transpositions of the elements of the given vector X. Then for an n-dimensional Trs(X) matrix
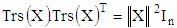 | (11) |
6.4. The Trs Matrix has Symmetrical Connectivity of the Elements of the First Row and Column and Antisymmetric Connectivity of the Other Elements Except the Diagonal Elements
- As indicated in (6) the first row and the first column of the Trs matrix contains the elements of the given vector X without inversions. We will prove that from the mutual orthogonality of the rows of Trs the matrix follows that the elements which are not contained in the first row and the first column are antisymmetric (skew-symmetric).We look at the Trs-fours (Trs0,0, Trs0,u, Trsu,0, Trsu,u), which contain the first diagonal element Trs0,0, element from the first row Trs0,u, element of the first column Trsu,0 and diagonal element Trsu,u. As Trs0,0=X0, Trs0,u=Xu, Tru,0=Xu then according Tr-property follows that diagonal element Tru,u = -X0, therefore diagonal elements of Trs the matrix except for Tr0,0 contain the first element of the given vector X with a negative sign Tru,u = -X0, u∈[1,n-1].Let’s now look at the Trs-fours of elements (Trsu,u, Trsu,v, Trsv,u, Trsv,v), u,v
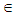 [1,n-1]., u≠v, which contain two diagonal elements Trsu,u and Trsv,v and two diagonally spaced elements Trsu,v and Trsu,v. As (shown above) Trsu,u = -X0.и Trsv,v = -X0, then according Trs-рproperty it follows that the diagonally spaced elements Trsu,v и Trsv,v have opposite signs Trsu,v = -Trsv,u Q.E.D.
[1,n-1]., u≠v, which contain two diagonal elements Trsu,u and Trsv,v and two diagonally spaced elements Trsu,v and Trsu,v. As (shown above) Trsu,u = -X0.и Trsv,v = -X0, then according Trs-рproperty it follows that the diagonally spaced elements Trsu,v и Trsv,v have opposite signs Trsu,v = -Trsv,u Q.E.D.6.5. The Trs Matrix Created from Unit Vector X is Matrix of Reflection
- Let’s have transpositions matrix with mutually orthogonal rows Trs(X), obtained from an arbitrary n-dimensional unit vector X=[x0,x1, … xn-1]T, ||X||=1, n∈[2,4,8].As shown in property 6.3, matrix Trs(X), obtained from unit vector is an orthogonal matrix, therefore ||det(Trs(X))||=1. We will prove that det(Trs(X))=-1, which will mean that Trs matrix is matrix of reflection.Proof:As proved in 6.4, Trs matrix has symmetric dependence of the elements of the first row and column and antisymmetric dependence of the other elements. Then the matrix obtained as a product of Trs(X) and a diagonal matrix D in which d1,1=-1 and di,i=1 for i≠1 can be represented as the sum of an skew-symmetric matrix S and matrix x0In, where In is an n-dimensional identity matrix as follows:
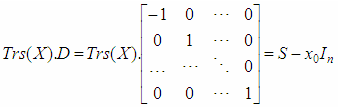 | (13) |
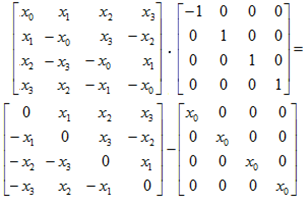 | Figure 8. Representing the product of Trs (X) and matrix of a single inversion as difference of a symmetric and diagonal matrix |
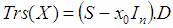 | (14) |
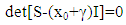 | (15) |
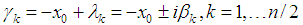 | (16) |
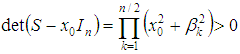 | (17) |
7. Obtaining n-dimensional Hadamard Matrix H(R)n for which the Rows of the Trs Matrix are Mutually Orthogonal
- As shown in 6.1. to obtain from (5) a Trs matrix whose rows are mutually orthogonal, it is enough the two-dimensional subvectors in the fours of elements in n-dimensional Hadamard matrix H(R)n to be mutually orthogonal (9). Given that the elements of Hadamard matrix are either +1 or −1, from (10) we get:
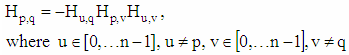 | (12) |
8. Practical Application of Trs Matrices
- By definition, Trs(X) is a matrix whose rows are mutually orthogonal and contain transpositions of a given vector X, while the first row contains the values of X without inversions. Therefore, if ||X||=1 then the multiplication of Trs(X/||X||) by X gives unit vector to the direction of the coordinate axis
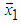
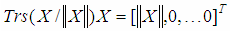 | (18) |
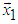 is base operation of the NRMG algorithm for obtaining an n-dimensional rotation matrix [1] and of algorithm for QR decomposition of a matrix [7], [13]. Base operation of those two algorithms is rotation (or reflection) of given n-dimensional vector to the direction of one of coordinate axes. For “dense” matrices as the most effective method is considered Householder reflection [2], [3], [13], while for “sparse” matrices more effective could be the method using Givens rotations.The use of Trs matrices is an alternative method, which in some cases may be more effective than both Householder reflections and Givens rotations. Tests and analysis of the algorithm show that obtaining an orthogonal Trs matrix of sizes 4 and 8 that rotates a given vector to the direction of one of the coordinate axes requires less processing time than obtaining such Housholder matrix. A description of the testing is given in "Numerical Experiments".Rotation of n-dimensional vector to the direction of the coordinate axis
is base operation of the NRMG algorithm for obtaining an n-dimensional rotation matrix [1] and of algorithm for QR decomposition of a matrix [7], [13]. Base operation of those two algorithms is rotation (or reflection) of given n-dimensional vector to the direction of one of coordinate axes. For “dense” matrices as the most effective method is considered Householder reflection [2], [3], [13], while for “sparse” matrices more effective could be the method using Givens rotations.The use of Trs matrices is an alternative method, which in some cases may be more effective than both Householder reflections and Givens rotations. Tests and analysis of the algorithm show that obtaining an orthogonal Trs matrix of sizes 4 and 8 that rotates a given vector to the direction of one of the coordinate axes requires less processing time than obtaining such Housholder matrix. A description of the testing is given in "Numerical Experiments".Rotation of n-dimensional vector to the direction of the coordinate axis 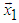 using Trs matrices.As is known [15], [20], [21], any positive integer n∈N, n<2m+1 can be represented in a binary number system as a polynomial in terms of 2 by coefficients ak=[0,1] as follows:
using Trs matrices.As is known [15], [20], [21], any positive integer n∈N, n<2m+1 can be represented in a binary number system as a polynomial in terms of 2 by coefficients ak=[0,1] as follows: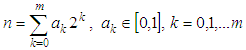 | (19) |
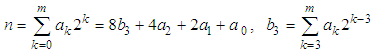 | (20) |
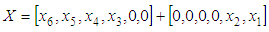 | (21) |
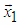 . The figure below shows graphically the transformation operations for 2, 4 and 8-dimensional vectors through Trs matrices. The unit for rotating a two-dimensional vector through a Trs matrix is equivalent to multiplying with Givens matrix for rotating a 2-dimensional vector in coordinate plane (xk, xk+1), but Trs matrix is matrix of reflection, while Givens matrix is matrix of rotation.
. The figure below shows graphically the transformation operations for 2, 4 and 8-dimensional vectors through Trs matrices. The unit for rotating a two-dimensional vector through a Trs matrix is equivalent to multiplying with Givens matrix for rotating a 2-dimensional vector in coordinate plane (xk, xk+1), but Trs matrix is matrix of reflection, while Givens matrix is matrix of rotation.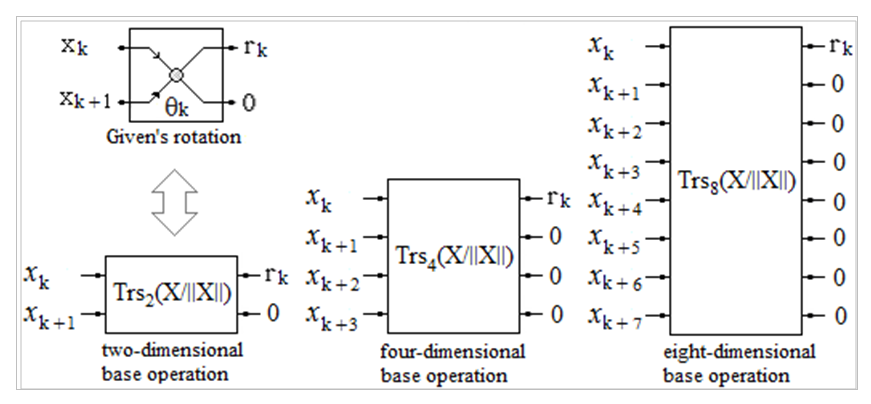 | Figure 9. Schema for transformation of 2, 4 and 8-dimensional vectors using Trs matrices |
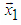 by means of Trs matrices can be represented by the following block diagram (Figure 10). From the first eight elements of the given 10-dimensional vector X, is obtained matrix Trs8(X8/||X8||), which reflects the 8- dimensional vector X8 to the direction of the axis
by means of Trs matrices can be represented by the following block diagram (Figure 10). From the first eight elements of the given 10-dimensional vector X, is obtained matrix Trs8(X8/||X8||), which reflects the 8- dimensional vector X8 to the direction of the axis 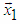 . From a two-dimensional vector X2=[x9,x10]T is obtained matrix Trs2(X2/||X2||), which reflects X2 to the direction of the axis
. From a two-dimensional vector X2=[x9,x10]T is obtained matrix Trs2(X2/||X2||), which reflects X2 to the direction of the axis 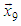 . In the second stage of the algorithm through matrix Trs2(X22/||X22||) the vector X22=[r8,r2]T is reflected in the coordinate plane (x1, x9) which gives 10-dimensional output vector Y=[r10,0,...,0]T. Since Trs are orthogonal matrices, then ||Y||=[r10,0,...,0]T =||X|| and consequently |r10|=||X||.
. In the second stage of the algorithm through matrix Trs2(X22/||X22||) the vector X22=[r8,r2]T is reflected in the coordinate plane (x1, x9) which gives 10-dimensional output vector Y=[r10,0,...,0]T. Since Trs are orthogonal matrices, then ||Y||=[r10,0,...,0]T =||X|| and consequently |r10|=||X||.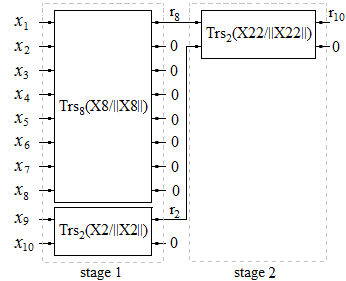 | Figure 10. Schema for rotation of 10-dimensional vector to the direction of axis 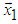 using Trs matrices using Trs matrices |
 | (21) |
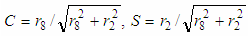
9. Numerical Experiments
- Has been created Matlab program to test the application of Trs matrices for QR decomposition [7], [8]. The following example gives the code of a program that performs QR decomposition of a matrix obtained with a random number generator using Trs matrices or Householder transformation.
 | Example 3. Code of Matlab for QR decomposition using Trs matrices or Householder reflection |
 | Example 4. Code of Matlab function, which returns orthogonal matrix M, that zeroes elements of k-th column under k-th index of R matrix using Trs block matrices |
 | Example 5. Code of Matlab function, which returns orthogonal matrix M, that zeroes elements of k-th column under k-th index of R matrix using Householder transformation |
10. Algorithmic Efficiency
- As is known [4], [10], [13], [17], [18], the Householder transformation is considered to be the most efficient and stable method for the QR decomposition of “deep” matrices.When obtaining a Householder matrix using the function Hous(x, k) for a given n-dimensional vector x, two normalizations of k-bit vectors and k2 multiplications is performed.When calculating a Trs matrix for vector X∈Rn where n = 4 or n = 8, using the function TrsMatrix(X), it calculates one normalizations of the given vector x and executes two nested cycles in which are executed n2 bitwise XOR operations.For comparison, when calculating a Householder matrix for vector X∈Rn using the Hous(X,1) function, it calculates two normalizations and performs two nested cycles in which 2n2 multiplications are performed.A C ++ test program was created1 to compare the execution time of functions to obtain an 8-bit Trs matrix and an 8-bit Householder matrix. The results of execution of C ++ test program shows that for the 4 and 8 dimensional vectors, the calculation of the Trs matrix requires less processing time than the calculation of the Householder matrix.However, when testing QR decomposition, the results show that for “dense” matrices, using the TrsTransforms function (which uses Trs matrices) instead of Hous(x,k) function (which uses Householder matrices) requires several times more execution time.
11. Conclusions
- In this article, we presents a special case of symmetric matrices, matrices of transpositions (Tr matrices) that are constructed from the elements of a given n-dimensional vector X∈Rn, n=2m, m∈N. An algorithm for obtaining matrices of transpositions with mutually orthogonal rows (Trs matrices) of dimensions 2, 4, and 8 as Hadamard product from the symmetric Tr matrix and Hadamard matrix is proposed and the possibility of using them for QR decompozition and obtaining a rotation matrix according to the NRMG algorithm is considered.
Note
- 1. https://www.researchgate.net/publication/335570264_Test_of_Trs_and_Housholder_Matrices
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML