L. A. Ukpebor
Department of Mathematics, Ambrose Alli University, Ekpoma, Nigeria
Correspondence to: L. A. Ukpebor, Department of Mathematics, Ambrose Alli University, Ekpoma, Nigeria.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
This paper proposes a four-point block method for the numerical solution of second order ordinary differential equations. In the construction of the method, interpolation and collocation techniques were involved, while Legendre Polynomial served as both the interpolation and collocation equations. The proposed scheme was analyzed and it was found to be A-stable, consistent and convergent.Numerical examples of ordinary differential equations were solved using the proposed method to test its performance. The results obtained compared favourably with other methods considered.
Keywords:
Interpolation, Collocation, Block method, Legendre Polynomial, A-stable, Consistent, Convergent
Cite this paper: L. A. Ukpebor, A 4-Point Block Method for Solving Second Order Initial Value Problems in Ordinary Differential Equations, American Journal of Computational and Applied Mathematics , Vol. 9 No. 3, 2019, pp. 51-56. doi: 10.5923/j.ajcam.20190903.01.
1. Introduction
This paper considered the general second-order ordinary differential equations, ODEs which we often encounter in the field of sciences, engineering and dynamic systems. They are generally written as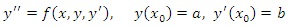 | (1) |
My intention in this paper is to derive a block scheme from the continuous linear multistep method of the form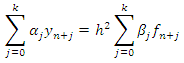 | (2) |
that can solve (1) above. Some authors have attempted solving (1) numerically by first reducing it to a system of first order equations. Notable among these authors are [1] and [2]. In spite of the success of this method, it suffers some setbacks. According to [3], the method is un-economical in terms of cost of implementation, increased computational burden and wastage of computer time and increased dimension of the resulting systems of equations to be solved.Some researchers have attempted solving (1) directly without reducing it to a first order ODEs by employing continuous linear multistep methods. See [4], [5] and [6]. According to [6], continuous linear multistep method have greater advantages over the discrete methods since they give better error estimates and provide simplified form, which allows easy approximation of solution at all interior points of the integration interval.Using linear multistep methods, several other researchers [7-17], have proposed methods in which the approximate solutions range from Power Series, Chebychev’s, Lagrange’s and Laguerre’s polynomials.In this paper, Legendre polynomial was used as basis function in generating the continuous linear multistep for the solution of (1).The plan of this paper is as follows: Section 1, introduction; Section 2, the derivation of the proposed method is presented. In Section 3, the stability and convergence analysis of the block method is given. In Section 4, numerical examples are considered. The paper ends with summary and conclusion in Section 5.
2. Materials and Methods
In this section, the mathematical formulation of the method is presented. I use Legendre polynomial as our approximate solution.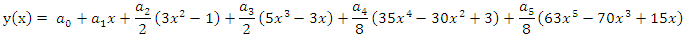 | (3) |
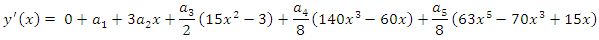 | (4) |
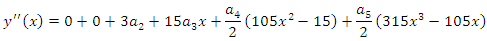 | (5) |
Interpolating (3) at the points 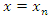 and
and 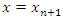 , we have
, we have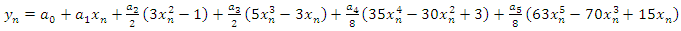 | (6) |
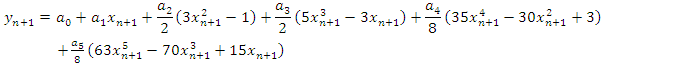 | (7) |
Also, collocating (5) at the points 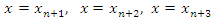 and
and 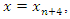 we have
we have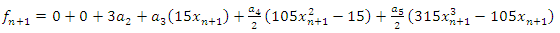 | (8) |
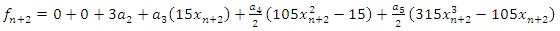 | (9) |
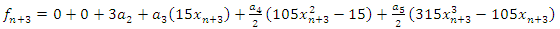 | (10) |
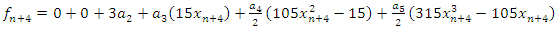 | (11) |
Putting (6-11) in matrix form gives below D matrix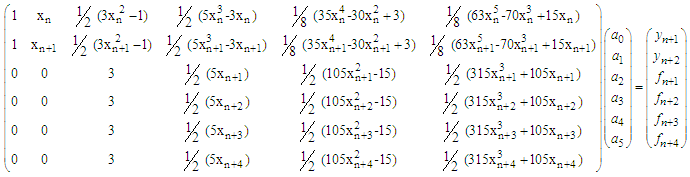 | (12) |
Solving (12) for the 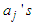 and substituting back into (3) and after much algebraic simplification, to obtained the multistep method of the form
and substituting back into (3) and after much algebraic simplification, to obtained the multistep method of the form 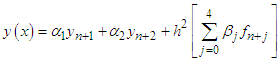 | (13) |
Where 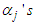 and
and 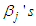 are continuous coefficients expressed as functions of
are continuous coefficients expressed as functions of 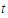 , whereAdopting Kayode et al (2018)
, whereAdopting Kayode et al (2018) 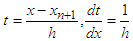 | (14) |
The coefficients of 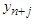 and
and 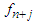 are obtained as:
are obtained as: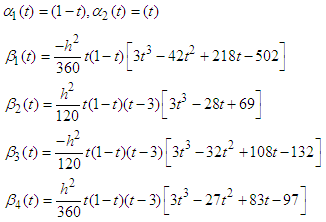 | (15) |
Evaluating (15) at 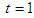 , the first derivatives of (15) at all the points and solve simultaneously gives the numerical integrators below
, the first derivatives of (15) at all the points and solve simultaneously gives the numerical integrators below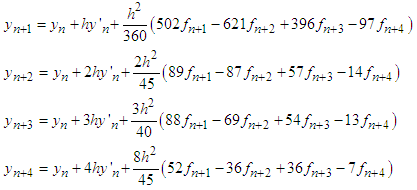 | (16) |
With the following derivatives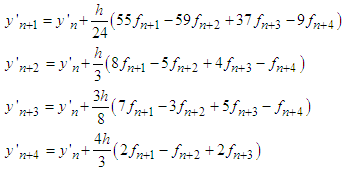 | (17) |
(16) and (17) are the required formulae for the implementation of the method.
3. Convergence Analysis of (OEBHF)
3.1. Order and Error Constants of the New Method
According to ([1, 16, 17]), the order of the new method in Equation (11) is obtained by using the Taylor series and it is found that the developed method has uniformly order four, with an error constants vector of: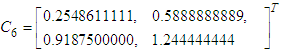
3.2. Consistency
Definition 3.1: The hybrid block method (7) is said to be consistent if it has an order more than or equal to one i.e. 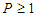 . Therefore, the method is consistent ([1, 4, 6]).
. Therefore, the method is consistent ([1, 4, 6]).
3.3. Regions of Absolute Stability (RAS)
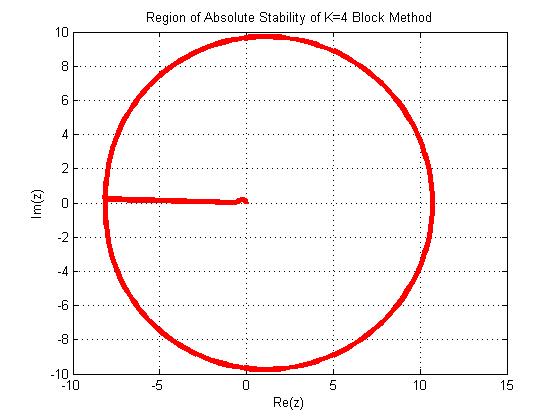 | Figure 1. Absolute Stability Region of the new method |
4. Numerical Implementation of the New Method
In this section, the accuracies and the performance the new developed methods is tested on two standard test problems from the recent literature. Two numerical experiments widely solved by Kayode et al (2018), and Kayode and Adeyeye (2013). The performance of the new developed method is shown in Tables 1-5, while table 6-7 shows the comparison of the new developed method with the selected problem in the existing method Kayode et al (2018), and Kayode and Adeyeye (2013) in terms of absolute errors and accuracies.Table 1. Results of Problem 1 with h=0.1
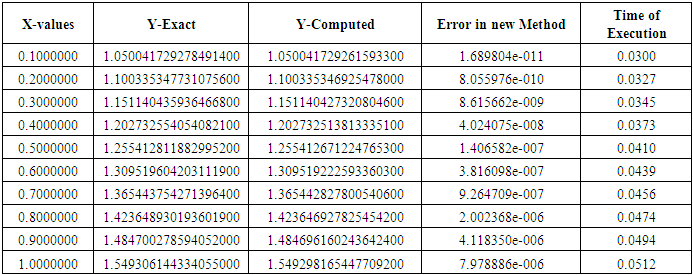 |
| |
|
Table 2. Results of Problem 1 with h=0.01
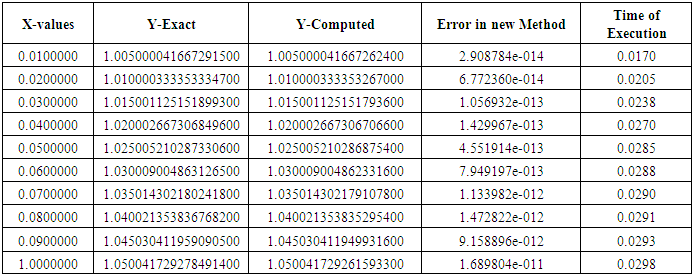 |
| |
|
Table 3. Results of Problem 1 with h=0.1/32
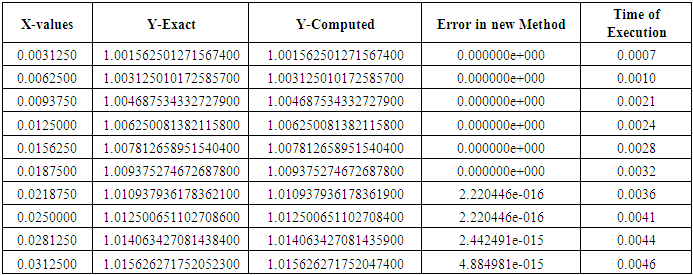 |
| |
|
Table 4. Results of Problem 2 with h =0.1
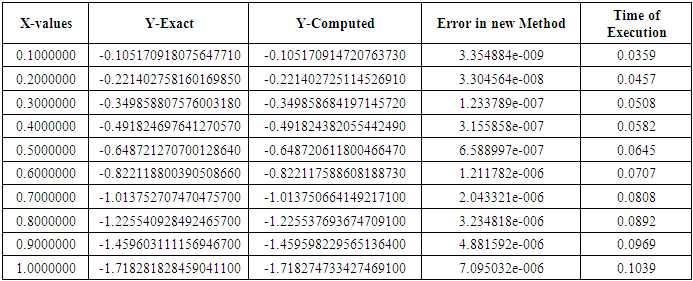 |
| |
|
Table 5. Results of Problem 2 with h =0.1/32
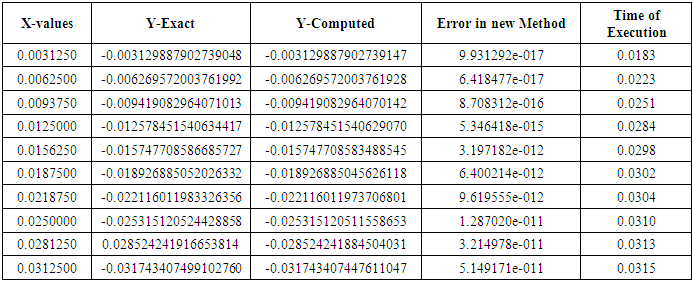 |
| |
|
Table 6. Comparison of Problem 1 with Kayode et al (2018) [15] with h =0.1/32
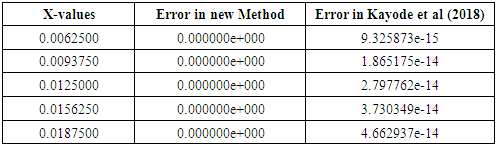 |
| |
|
Table 7. Comparison of Problem 2 with Kayode and Adeyeye [18]
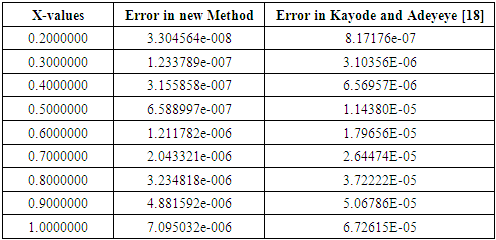 |
| |
|
Problem I: Considered a non-linear second order ordinary differential equations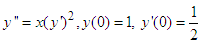 Exact solution:
Exact solution: 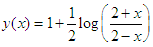 Source: Kayode et al (2018)Problem II: Considered a linear second order ordinary differential equations
Source: Kayode et al (2018)Problem II: Considered a linear second order ordinary differential equations 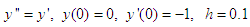 Exact solution
Exact solution 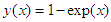 Source: Kayode and Adeyeye (2013)
Source: Kayode and Adeyeye (2013)
5. Summary and Conclusions
In this paper, the derivation, analysis and implementation of a four-point block method for the solution of second order ordinary differential equations is presented. The method was developed using the technique of interpolation and collocation and it was found to be A-stable, consistent and convergent. On implementation, two standard numerical examples were solved and the results show that the new proposed method is efficient and compared favorably with other methods in the literature, they were very close to the exact solutions.
References
| [1] | Lambert J.D, “computational methods in ordinary differential equations”, John Wiley, New York, 1973. |
| [2] | Fatunla S.O, “Numerical methods for initial value problems in ordinary differential equations”, New York, Academic Press, 1988. |
| [3] | Kayode S.J. and Adegboro J.O., “Predator-corrector Linear Multistep Method for Direct Solution of Initial Value Problems of Second Order Ordinary Differential Equations”, Asian Journal of Physical and Chemical Sciences, 6(1): 1-9, 2018. |
| [4] | Onumanyi P., Fatokun J., and Adejo B.O., “Accurate numerical differentiation by continuous integrators for ordinary differential equations”, Journal of the Nigerian Mathematical Society, Vol. 27, Pp 69-90, 2008. |
| [5] | Kayode S.J., “An improved numeror method for direct solution of general second order initial value problems of ordinary differential equations”. Proceedings of the seminar organized by the national mathematical centre, Abuja, Nigeria, 2005. |
| [6] | Awoyemi D.O., “A new sixth-order algorithm for general second order ordinary differential equations”. International Journal of Computer Mathematics, 2001; 77: 117-124. |
| [7] | Ehigie J.O., Okunuga S.A., Sofoluwe A.B. and Akanbi M.A., “One generalized 2-step continuous linear multistep method of hybrid type for the integration of second order ODEs.” Journal of Scholars Research Library 2(6): 362-372. |
| [8] | Odekunle M.R., Adesanya A.O., Sunday J., “A new Block Integrator for the solution of ivps of first-order ordinary differential equations.” International Journal of Pure and Applied Sciences and Technology 11(1), Pp 92-100. |
| [9] | Abualnaja K.M., “Ablock procedure with linear multistep methods using Legendre Polynomial for solving ODEs.” Journal of Applied Mathematics, 6, (717-732). http//dx.doi.org/10.4236/am.2015.64067. |
| [10] | Adeniyi R.B. and ADeyefa E.O., “Chebyshev collocation Approach for continuous formulation of implicit hybrid methods for ivps in second order ODEs”. Journal of Mathematics, Vol. 6, Issue 4, Pp (09-12), 2013. |
| [11] | Adesanya A.O., Anake T.A. and Oghonyon G.J., “Continuous implicit method for the solution of general second order ODEs”. Journal of Nigeria Association of Mathematical Physics, Pp 71-78, 2009. |
| [12] | Areo E.A., Ademiluyi R.A. and Babatola P.O., “Three-step Hybrid Linear Multistep Method for the solution of First-order initial value problems in ODEs”. Journal of Mathematical Physics. Vol. 4 No. 8, pp (261-266), 2011. |
| [13] | Fatokun J.O., Aimufua G.I.O. and Ajibola I.K.O., “An efficient direct collocation method for the integration of general second order initial value problem.” Journal of Institute of Mathematics and Computer Science, 21, 227-327. |
| [14] | Fatokun J.O., Onumanyi P. and Sirisena U., “A multistep collocation based on exponential basis for stiff initial value problems”. Nigerian Journal of Mathematics and Applications, 12, 207-223. |
| [15] | S. J. Kayode, O. S. Ige, F. O. Obarhua and E. O. Omole (2018): An Order Six Stormer-cowell-type Method for Solving Directly Higher Order Ordinary Differential Equations. Asian Research Journal of Mathematics 11(3): 1-12. |
| [16] | L. A. Ukpebor, E. O. Omole and L. O. Adoghe (2019): Fully Implicit Five-quarters Computational Algorithms of Order Five for Numerical Approximation of Second Order IVPs in ODEs. Journal of Advances in Mathematics and Computer Science 30(4): 1-15. |
| [17] | Adoghe L.O and Omole E. O (2019): A Two-step Hybrid Block Method for the Numerical Integration of Higher Order Initial Value Problems of Ordinary Differential Equations. World Scientific News Journal (118) 236-250. |
| [18] | Kayode S. J, Adeyeye O. Two-step two-point hybrid methods for general second order differential equations. Africa Journal of Computer and Mathematics Science Research; 2013. |


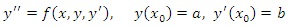
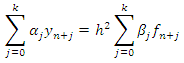
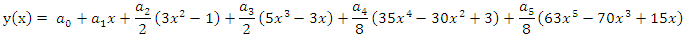
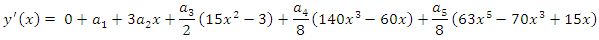
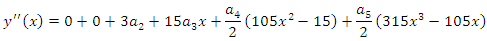
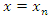 and
and 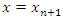 , we have
, we have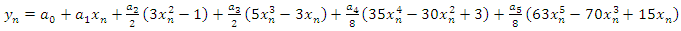
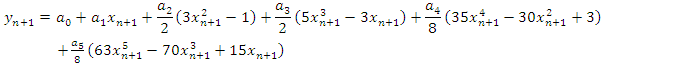
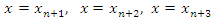 and
and 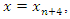 we have
we have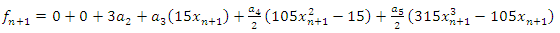
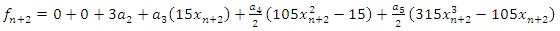
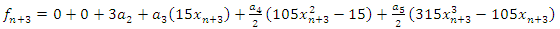
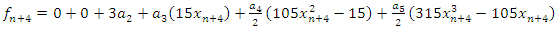
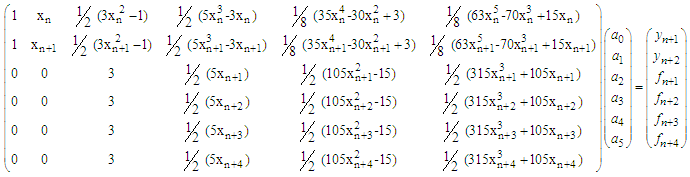
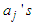 and substituting back into (3) and after much algebraic simplification, to obtained the multistep method of the form
and substituting back into (3) and after much algebraic simplification, to obtained the multistep method of the form 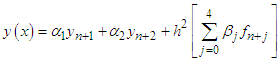
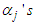 and
and 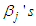 are continuous coefficients expressed as functions of
are continuous coefficients expressed as functions of 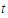 , whereAdopting Kayode et al (2018)
, whereAdopting Kayode et al (2018) 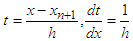
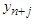 and
and 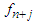 are obtained as:
are obtained as: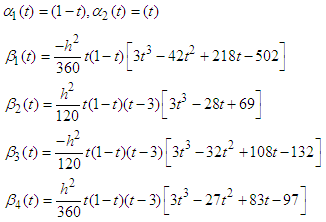
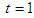 , the first derivatives of (15) at all the points and solve simultaneously gives the numerical integrators below
, the first derivatives of (15) at all the points and solve simultaneously gives the numerical integrators below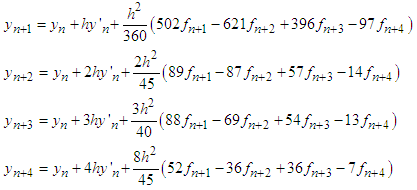
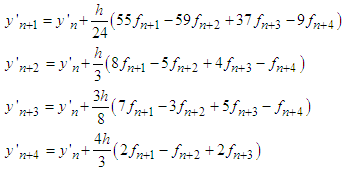
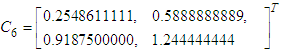
 . Therefore, the method is consistent ([1, 4, 6]).
. Therefore, the method is consistent ([1, 4, 6]).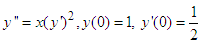 Exact solution:
Exact solution: 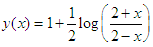 Source: Kayode et al (2018)Problem II: Considered a linear second order ordinary differential equations
Source: Kayode et al (2018)Problem II: Considered a linear second order ordinary differential equations 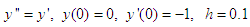 Exact solution
Exact solution 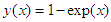 Source: Kayode and Adeyeye (2013)
Source: Kayode and Adeyeye (2013) Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML






