1. Introduction

Ann is a simplified mathematical model of the human brain, It can be implemented by both electric elements and computer software. It is a parallel distributed processor with large numbers of connections, it is an information processing system that has certain performance characters in common with biological neural networks. Ann has been developed as generalizations of mathematical models of human cognition or neural biology, based on the assumptions that:

1- Information processing occurs at many simple elements called neurons that are fundamental to the operation of Ann's.

2- Signals are passed between neurons over connection links.

3- Each connection link has an associated weight which, in a typical neural net, multiplies the signal transmitted.

4- Each neuron applies an action function (usually nonlinear) to its net input (sum of weighted input signals) to determine its output signal [15].

The units in a network are organized into a given topology by a set of connections, or weights.

Ann is characterized by [30]:

1- Architecture: its pattern of connections between the neurons.

2- Training Algorithm: its method of determining the weights on the connections.

3- Activation function.

Ann are often classified as single layer or multilayer. In determining the number of layers, the input units are not counted as a layer, because they perform no computation. Equivalently, the number of layers in the net can be defined to be the number of layers of weighted interconnects links between the slabs of neurons [46].

1.1. Multilayer Feed Forward Architecture [22]

In a layered neural network the neurons are organized in the form of layers. We have at least two layers: an input and an output layer. The layers between the input and the output layer (if any) are called hidden layers, whose computation nodes are correspondingly called hidden neurons or hidden units. Extra hidden neurons raise the network’s ability to extract higher-order statistics from (input) data.

The Ann is said to be fully connected in the sense that every node in each layer of the network is connected to every other node in the adjacent forward layer; otherwise the network is called partially connected. Each layer consists of a certain number of neurons; each neuron is connected to other neurons of the previous layer through adaptable synaptic weights w and biases b.

1.2. Literature Review

Pan and Duraisamy in 2018 [33] studied the use of feedforward neural networks (FNN) to develop models of non-linear dynamical systems from data. Emphasis is placed on predictions at long times, with limited data availability. Inspired by global stability analysis, and the observation of strong correlation between the local error and the maximal singular value of the Jacobian of the ANN, they introduced Jacobian regularization in the loss function. This regularization suppresses the sensitivity of the prediction to the local error and is shown to improve accuracy and robustness. Comparison between the proposed approach and sparse polynomial regression is presented in numerical examples ranging from simple ODE systems to nonlinear PDE systems including vortex shedding behind a cylinder, and instability-driven buoyant mixing ow. Furthermore, limitations of feedforward neural networks are highlighted, especially when the training data does not include a low dimensional attractor. The need to model dynamical behavior from data is pervasive across science and engineering. Applications are found in diverse fields such as in control systems [43], time series modeling [41], and describing the evolution of coherent structures [12]. While data-driven modeling of dynamical systems can be broadly classified as a special case of system identification [23], it is important to note certain distinguishing qualities: the learning process may be performed off-line, physical systems may involve very high dimensions, and the goal may involve the prediction of long-time behavior from limited training data. Artificial neural networks (ANN) have attracted considerable attention in recent years in domains such as image recognition in computer vision [17, 37] and in control applications [12]. The success of ANNs arises from their ability to effectively learn low-dimensional representations from complex data and in building relationships between features and outputs. Neural networks with a single hidden layer and nonlinear activation function are guaranteed to be able to predict any Borel measurable function to any degree of accuracy on a compact domain [16]. The idea of leveraging neural networks to model dynamical systems has been explored since the 1990s. ANNs are prevalent in the system identification and time series modeling community [19, 28, 29, 35], where the mapping between inputs and outputs is of prime interest. Billings et al. [5] explored connections between neural networks and the nonlinear autoregressive moving average model (NARMAX) with exogenous inputs. It was shown that neural networks with one hidden layer and sigmoid activation function represent an infinite series consisting of polynomials of the input and state units. Elanayar and Shin [13] proposed the approximation of nonlinear stochastic dynamical systems using radial basis feedforward neural networks. Early work using neural networks to forecast multivariate time series of commodity prices [9] demonstrated its ability to model stochastic systems without knowledge of the underlying governing equations. Tsung and Cottrell [44] proposed learning the dynamics in phase space using a feedforward neural network with time-delayed coordinates. Paez and Urbina [31, 32, 45] modeled a nonlinear hardening oscillator using a neural network-based model combined with dimension reduction using canonical variate analysis (CVA). Smaoui [40, 41, 42] pioneered the use of neural networks to predict fluid dynamic systems such as the unstable manifold model for bursting behavior in the 2-D Navier-Stokes and the Kuramoto-Sivashinsky equations. The dimensionality of the original PDE system is reduced by considering a small number of proper orthogonal decomposition (POD) coefficients [4]. Interestingly, similar ideas of using principal component analysis for dimension reduction can be traced back to work in cognitive science by Elman [14]. Elman also showed that knowledge of the intrinsic dimensions of the system can be very helpful in determining the structure of the neural network. However, in the majority of the results [40, 41, 42], the neural network model is only evaluated a few time steps from the training set, which might not be a stringent performance test if longer time predictions are of interest. ANNs have also been applied to chaotic nonlinear systems that are challenging from a data-driven modeling perspective, especially if long time predictions are desired. Instead of minimizing the pointwise prediction error, Bakker et al. [3] satisfied the Diks’criterion in learning the chaotic attractor. Later, Lin et al. [20] demonstrated that even the simplest feedforward neural network for nonlinear chaotic hydrodynamics can show consistency in the time-averaged characteristics, power spectra, and Lyapunov exponent between the measurements and the model. A major difficulty in modeling dynamical systems is the issue of memory. It is known that even for a Markovian system, the corresponding reduced-dimensional system could be non-Markovian [10, 34]. In general, there are two main ways of introducing memory effects in neural networks. First, a simple workaround for feedforward neural networks (FNN) is to introduce time delayed states in the inputs [11]. However, the drawback is that this could potentially lead to an unnecessarily large number of parameters [18]. To mitigate this, Bakker [3] considered following Broomhead and King [6] in reducing the dimension of the delay vector using weighted principal component analysis (PCA). The second approach uses output or hidden units as additional feedback. As an example, Elman’s network [18] is a recurrent neural network (RNN) that incorporates memory in a dynamic fashion. Miyoshi et al. [25] demonstrated that recurrent RBF networks have the ability to reconstruct simple chaotic dynamics. Sato and Nagaya [38] showed that evolutionary algorithms can be used to train recurrent neural networks to capture the Lorenz system. Bailer-Jones et al. [2] used a standard RNN to predict the time derivative in discrete or continuous form for simple dynamical systems; this can be considered an RNN extension to Tsung’s phase space learning [44]. Wang et al. [47] proposed a framework combining POD for dimension reduction and long-short-term memory (LSTM) recurrent neural networks and applied it to a fluid dynamic system.

1.3. Fast Fourier Transform

The first to propose the techniques that we now call the fast Fourier transform (FFT) for calculating the coefficients in a trigonometric expansion of an asteroid’s orbit in 1805 [8]. However, Fast Fourier transform is an algorithm that calculates the value of the discret Fourier transform in faster. the speed this algorithm Is due to the fact that it does not calculate the parts that are equal to zero. the algorithm is discovered by James W. Cooley and John W. Tukey who published the algorithm in 1965 [11]

As know today

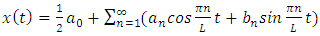(1)

The coefficients can be datermain as follows :

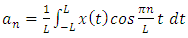(2)

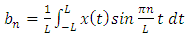(3)

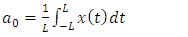(4)

The discrete Fourier transform (DFT) is one of the most powerful tools in Digital signal processing. The DFT enables us to conveniently analyze and Design systems in frequency domain [1] and the formal as:

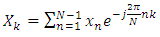(5)

2. Logistic Map

In 1845, Pierre Verhulst proposed a logistic map, which is a simple non-linear dynamical map. A logistic map is one of the most popular and simplest chaotic maps. Logistic map became very popular after it was exploited in 1979 by the biologist Robert M. May [24] [21]. The logistic map is a polynomial mapping, a complex chaotic system, the behaviour of which can arise from very simple non-linear dynamical equations. The logistic map equation is written as [26]:

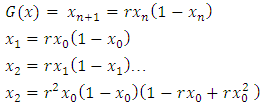(6)

where x_n is a number between zero and one, x₀ represents the initial population, and r is a positive number between zero and four.

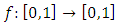The logistic map is one of the chaotic maps; it is highly sensitive to change in its parameter value, where a different value of the parameter r will produce a different sketches. Its transformation function is which is defined in the above equation (6). From the onset of chaos, a seemingly random jumble of dots, the behavior of the logistic map depends mainly on the values of two variables (r, x0); by changing one or both variables’ values we can observe different logistic map behavior’s. The population of a logistic map will die out if the value of r is between 0 and 1, and the population will be quickly stabilized on the value (1- r )/r if the value of r is between 1 and 3. Then, the population will oscillate between two values if the value of parameter r is between 3 and 3.45. After that, with values of parameter r between 3.45 and 4 the periodic fluctuation becomes significantly more complicated. Finally, most of the values after 3.57 show chaotic behaviour.

In the logistic map 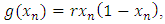the function result depends on the value of parameter r, where different values of r will give quite different pictures. We can note that g(x₁) = x₂ and g(x₂) = x₁, that mean g(g(x₂)) = x₁ and g(g(x₁)) = x₂. According to Alligood et al. (1996) the periodic fluctuation between x₁, x₂ is steady and attracts orbits (trajectories). Therefore, there are a minimum number of iterations of the orbit to repeat the point. There are obvious differences between the behaviour of the exponential model and the logistic model’s behaviour. [24, 21]

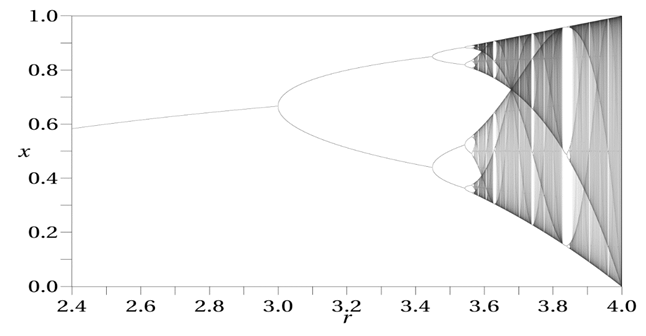Figure 1. Bifurcation diagram of the Logistic map [26]

2.1. Noisy Logistic map (NG) Solution

In this section we will explain how this approach can be used to find the approximate solution of the noisy logistic map that is stated in equation (6).

NG(x) is the solution to be computed. Let y_t(x, p) denotes a trial solution with adjustable parameters p.

In the proposed approach, the trial solution y_t employs a FFNN and the parameters p corresponding to the weights and biases of the neural architecture. We choose a form for the trial function y_t(x) such that y_t(x,p) = N(x, p) where N(x, p) is a single-output FFNN with parameters (weights) p and n input units fed with the input vector x.

2.2. Computation of the Gradient

The error corresponding to each input vector x_i is the value E (x_i) which has to force near zero. Computation of this error value involves not only the FFNN output but also the derivatives of the output with respect to any of its inputs. Therefore, for computation the gradient of the error with respect to the network weights, consider a multilayer FFNN with n input units (where n is the dimensions of the domain), two hidden layer with H sigmoid units,q hidden layer and a linear output unit.

For a given input vector x ( x₁, x₂, …, x_n ) the output of the FFNN is:

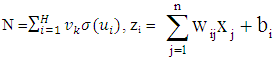and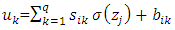

w_ij denotes the weight connecting the input unit j to the hidden unit i

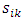denotes the weight connecting the hidden unit i to the hidden unit k

v_k denotes the weight connecting the hidden unit k to the out put unit,

b_i denotes the bias of hidden unit i,

b_ik denotes the bias of hidden unit i to the hidden unit k, and

σ is the transfer function

The gradient of suggest FFNN, with respect to the coefficients of the FFNN can be computed as:

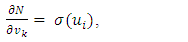(7)

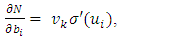(8)

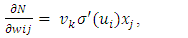(9)

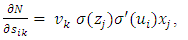(10)

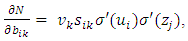(11)

The derivative of the error performance with respect to the FFNN coefficients can be defined and then it is easy to find minimization solution.

3. Suggested Networks

It is well known that a multilayer FFNN consist one hidden layer can approximate any function to any accuracy [27], but dynamical maps they have more completed behavior than other functions, thus, we suggest FFNN contains two hidden layer, one input and one output to estimate a solution for dynamic maps.

The suggested network divided the inputs in to two parts 60% for training and 40% for testing. The error quantity to be minimized is given by:

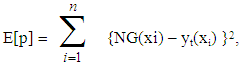(12)

Where x_i ∈ [0, 1]. It is easy to evaluate the gradient of the performance with respect to the coefficient. Using (7) – (11). The training progress algorithm of FFNN with supervises training and BFGS algorithm is given as follows. Assume that there are one nodes in the First layer (input layer), the second layer (hidden layer) consist with ten nodes, the third layer (hidden layer) consist with five nodes and the fourth layer (output layer) consist with one node.

Following the steps of the technique as an algorithm,

Step 0: input and target.

Insert the input (x: x₁, x₂, x₃,…., x_n) and the target.

Step 1: allocating inputs.

Each input goes to each neurons with a hidden layer.

Step 2: initialization weights.

We initial weights and bias from the uniform distribution respectively for all connection in the neural network.

Step 3: select the following.

- parameter epoch

- parameter goal

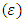- performance function (MSE)

Step 4: calculations in each node in the first hidden layer.

In each node in hidden layer, computing the sum of the product of weights and inputs and adding the result to the bias.

Step 5: compute the output of each node for the first hidden layer.

Take the active function for sum value in step4, then its output is sent to the second hidden layer as input.

Step 6: calculations in each node in the second layer.

In each node in second hidden layer, computing the sum of the product of weights and inputs and adding the result to the bias.

Step 7: compute the output of each node for the second hidden layer.

Take the active function for sum value in step 6, then its output is sent to the output layer as input.

Step 8: calculations in output layer.

There is only one neuron (node) in the output layer. The node sum is the product of weights by inputs.

Step 9: compute the output of node in output layer

The value of active function for node output is also considered as the output of overall network.

Step 10: compute the mean square error (MSE).

The mean square error is computed as follows

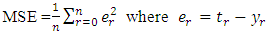the MSE is a measure of performance.

Step 11: The checking.

When 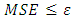such that 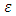is small value close to zero, then stop the training and the bias and weights are sent. Otherwise training process goes to the next step.

Step 12: when select the training rule, the low for update weights and bias between the hidden layer and the output layer are calculated

Step 13: the update weights and bias in output layer.

At end for each iteration, the weights and bias are updating as follows: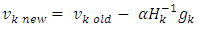

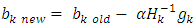
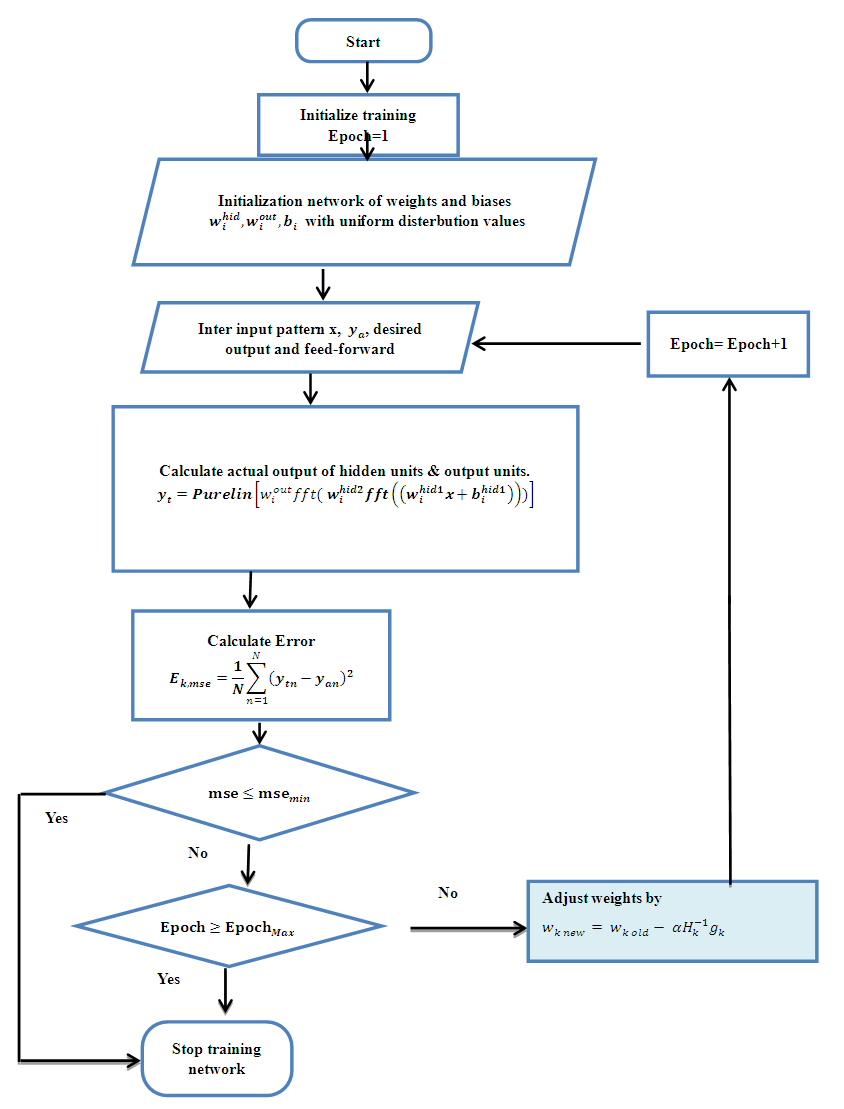Figure 2. Flowchart for training algorithm with BFGS

When (new) means the current iteration and (old) means the previous iteration,

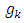represent the gradient for weights and bias, 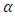is the parameter selected to minimize the performance function along the search direction, 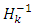represent the invers hessian matrix, v is the weight in the output layer and b is the bias.

Step 14: the update of weights and bias in the first hidden layer.

Each hidden node in the first hidden layer updates the weights and bias as follow:

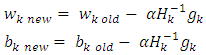Where w is the weight of hidden layer and b is the bias.

Step 15: the update of weights and bias in the second hidden layer as follow.

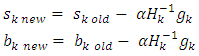Where s is the weight of hidden layer and b is the bias.

Step 16: return to step2 for next iteration.

4. Data Description

We know that for each starting point in dynamical map there are a minimum number of iterations of the orbit to repeat a point. So we choose number of initial points and iterated until reaching a point. There are initial points have thousands of iterations until reaching a point a gain, but the ability of personal computer will restrict us to take all these points. In addition, the higher value of the Bifurcation parameter implicit to complicate the calculations. For that reason, we will take the maximum capacity of the computer which is a one hundred point for initial point exceeding 100 iterations distributed on all the domain map evenly and the number of iterations of points was found by the program MATLAB R2010a.

4.1. Training for Noisy Logistic Map

To design FFNN that is not sensitive to noise for this case, we use the propose network with FFT as transfer function to train the data with noise, it is suitable to choose the maximum number of epochs, when the noisy data have noise of (uniform, normal and logistic) distributions and we take for all noises value of variance (0.05, 0.5, 15). We train this case with noise with three types of transfer functions Tansig, logsig and FFT. It is worth to mention that the run size is k=1000.

4.2. Uniform Distribution [36]

A uniform distribution is one have a constant probability. The probability density function and cumulative distribution function for continuous uniform distribution on the interval [a, b] are

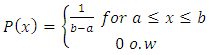(13)

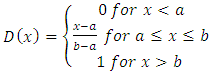(14)

One can generate values from Uniform random variable as follows,

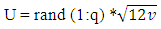(15)

Where q is represent the number point and v is represent the variance.

4.3. Normal Distribution [36]

Let x be a normally distributed random variable with mean 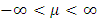and variance 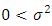, where 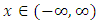with probability density function and cumulative distribution function are respectively,

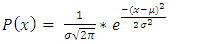(16)

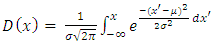(17)

One can generate values from Normal random variable as follows,

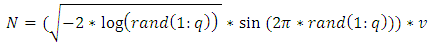(18)

Where q is represent the number point and v is represent the variance.

4.4. Logistic Distribution [36]

Let x be a Logistic distributed random variable with parameters 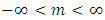and 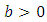, where 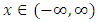with probability density function and cumulative distribution function are respectively,

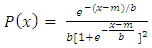(19)

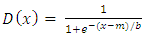(20)

One can generate values from Logistic random variable as follows,

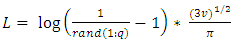(21)

Where q is represent the number point and v is represent the variance.

4.5. Training the Case with Uniform Noise

We train case with uniform noise and variances 0.05, 0.5 and 15. Table from (1) to (9) contain the results.

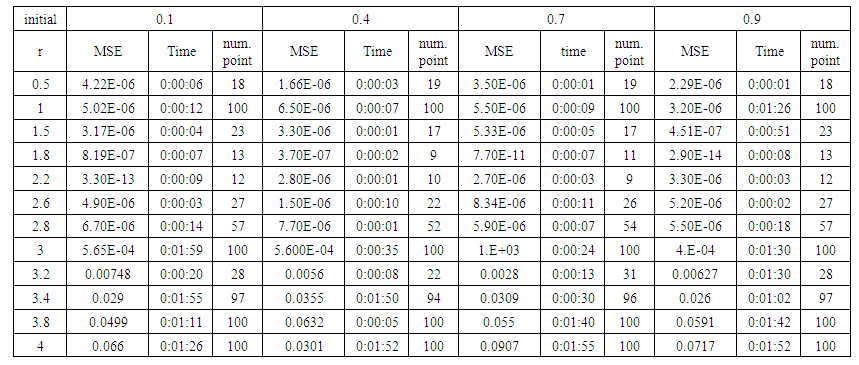Table (1). Time and MSE of approximate solution after many training trials with uniform noise by using tansig transfer function when the variance equal to 0.05

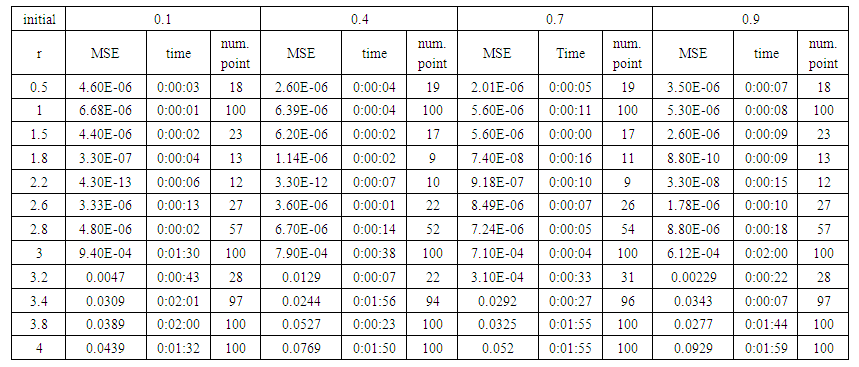Table (2). Time and MSE of approximate solution after many training trials with uniform noise by using logsig transfer function when the variance equal to 0.05

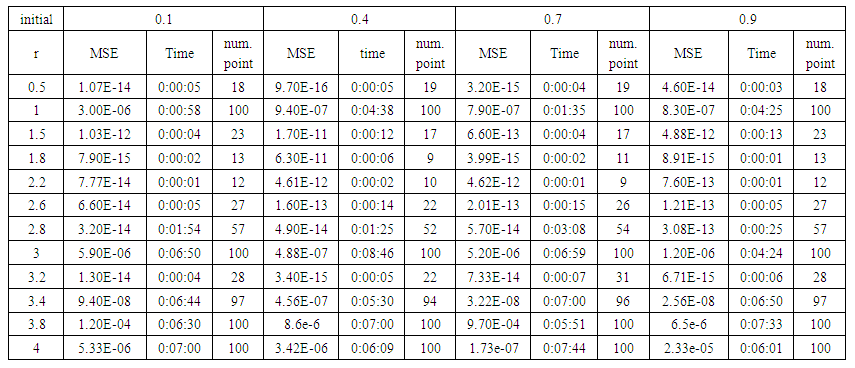Table (3). Time and MSE of approximate solution after many training trials with uniform noise by using FFT transfer function when the variance equal to 0.05

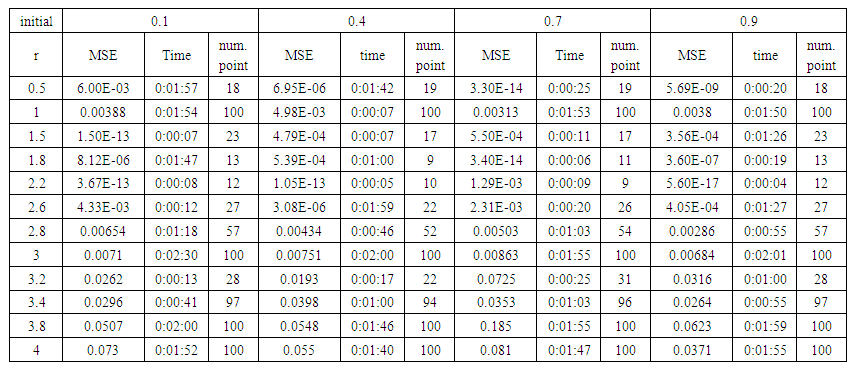Table (4). Time and MSE of approximate solution after many training trials with uniform noise by using tansig transfer function when the variance equal to 0.5

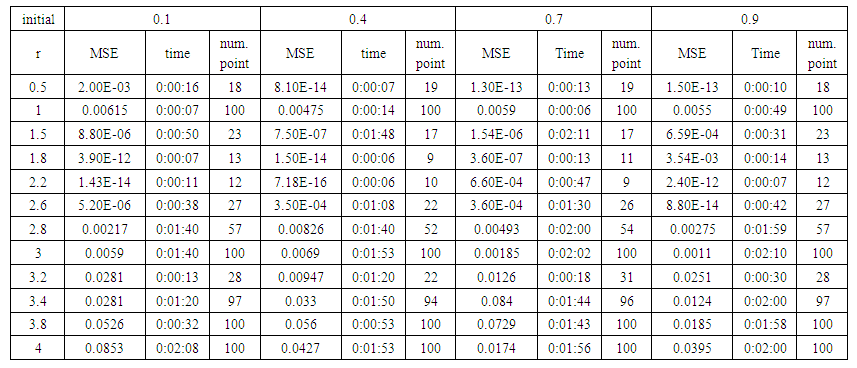Table (5). Time and MSE of approximate solution after many training trials with uniform noise by using logsig transfer function when the variance equal to 0.5

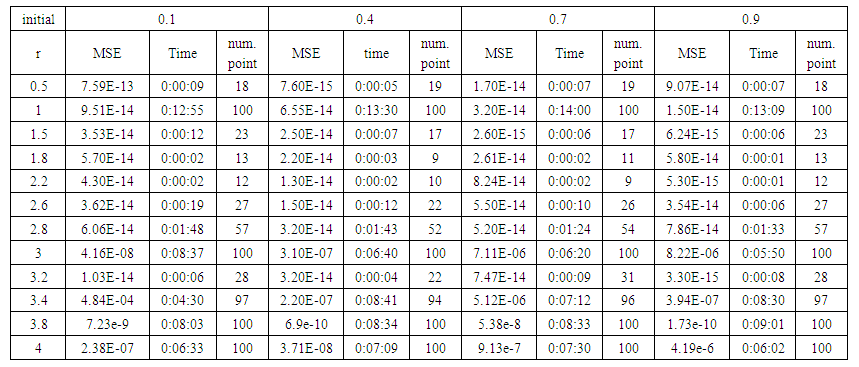Table (6). Time and MSE of approximate solution after many training trials with uniform noise by using FFT transfer function when the variance equal to 0.5

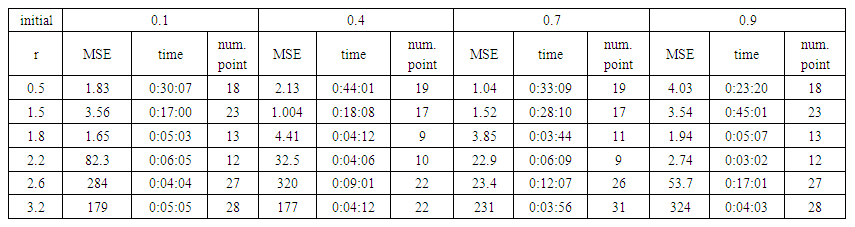Table (7). Time and MSE of approximate solution after many training trials with uniform noise by using logsig transfer function when the variance equal to 15

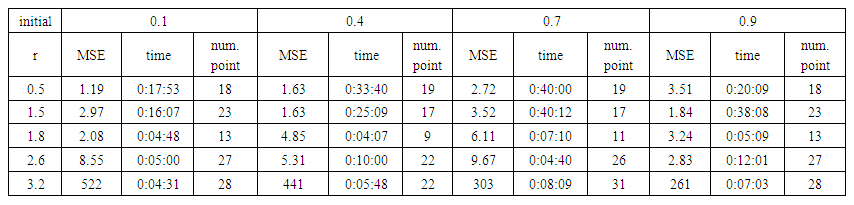Table (8). Time and MSE of approximate solution after many training trials with uniform noise by using tansig transfer function when the variance equal to 15

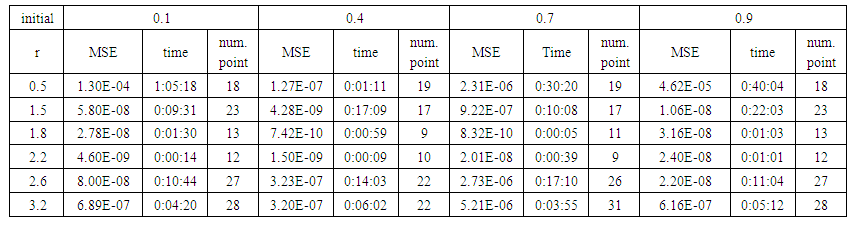Table (9). Time and MSE of approximate solution after many training trials with uniform noise by using FFT transfer function when the variance equal to 15

4.6. Training for Case with Normal Noise

We train case with normal noise and variances 0.05, 0.5 and 15. Table from (10) to (18) contain the results.

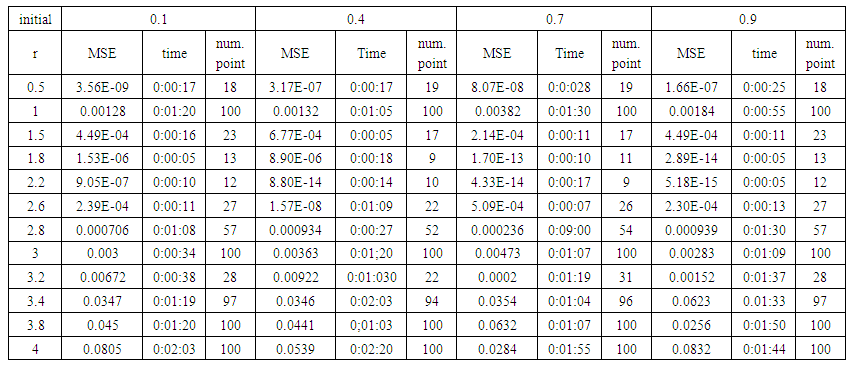Table (10). Time and MSE of approximate solution after many training trials with normal noise by using logsig transfer function when the variance equal to 0.05

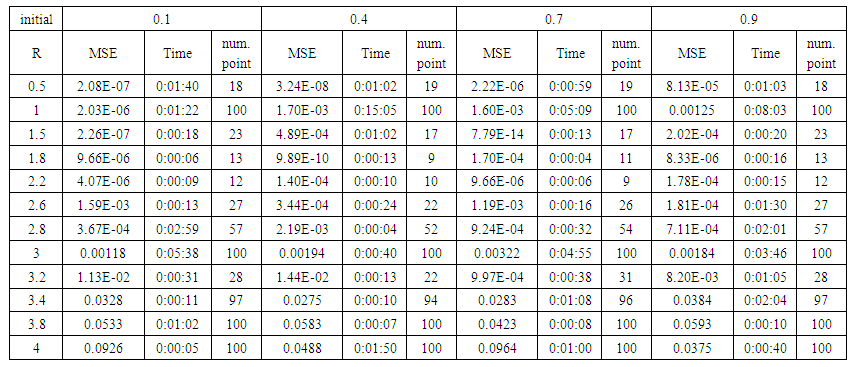Table (11). Time and MSE of approximate solution after many training trials with normal noise by using tansig transfer function when the variance equal to 0.05

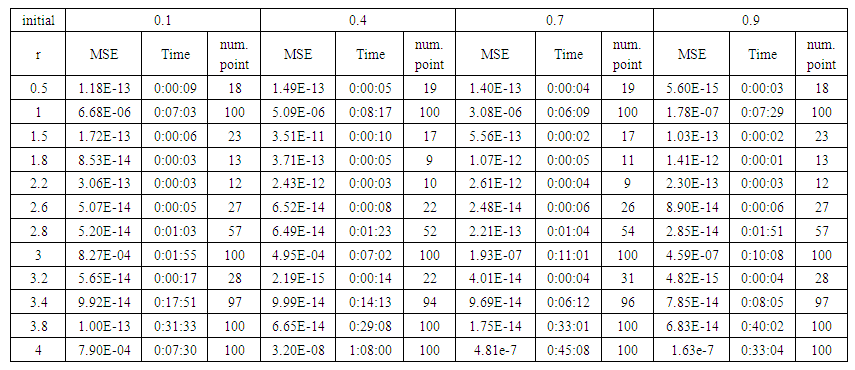Table (12). Time and MSE of approximate solution after many training trials with normal noise by using FFT transfer function when the variance equal to 0.05

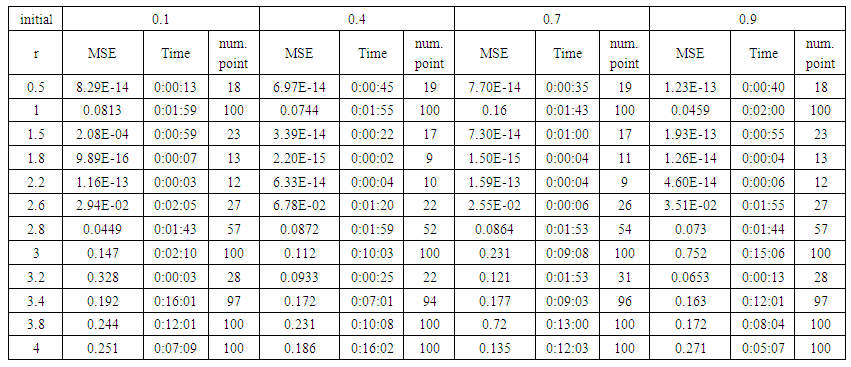Table (13). Time and MSE of approximate solution after many training trials with normal noise by using logsig transfer function when the variance equal to 0.5

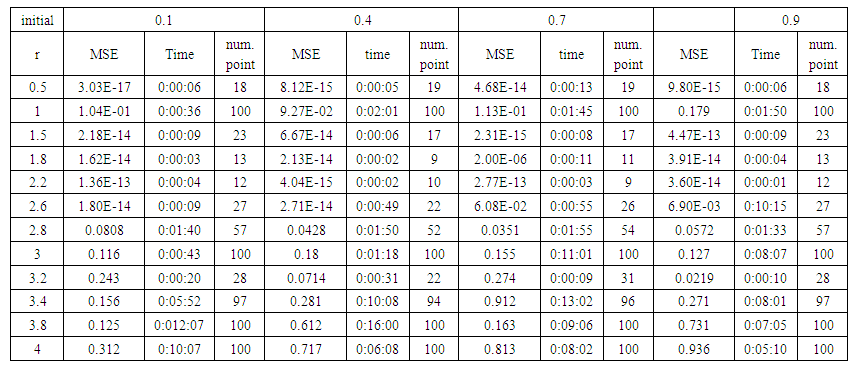Table (14). Time and MSE of approximate solution after many training trials with normal noise by using tansig transfer function when the variance equal to 0.5

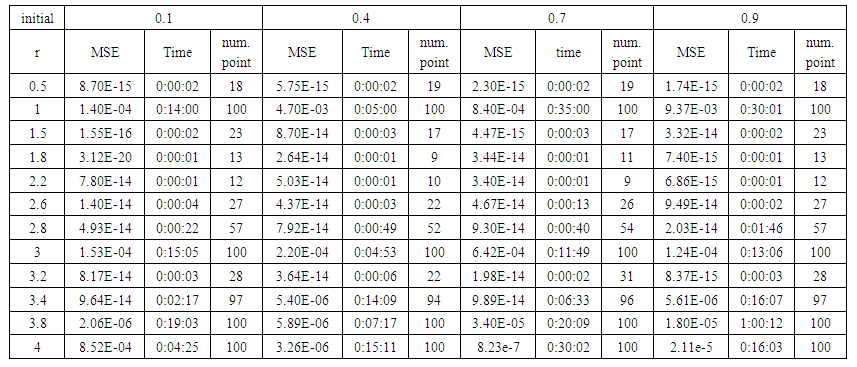Table (15). Time and MSE of approximate solution after many training trials with normal noise by using FFT transfer function when the variance equal to 0.5

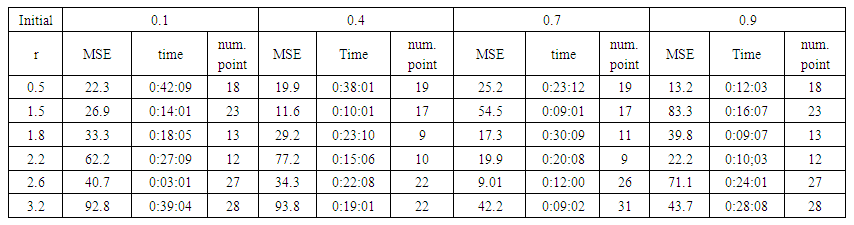Table (16). Time and MSE of approximate solution after many training trials with normal noise by using logsig transfer function when the variance equal to 15

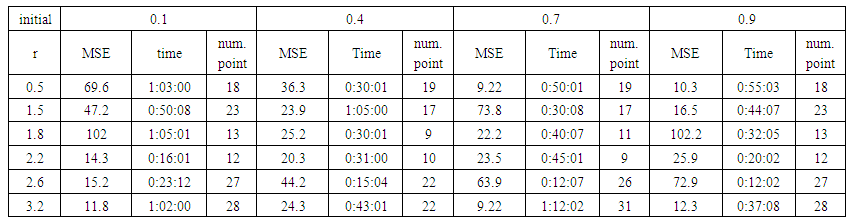Table (17). Time and MSE of approximate solution after many training trials with normal noise by using tansig transfer function when the variance equal to 15

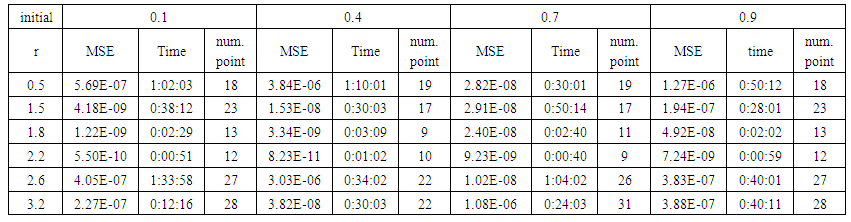Table (18). Time and MSE of approximate solution after many training trials with normal noise by using FFT transfer function when the variance equal to 15

4.7. Training for Case with Logistic Noise

We train case with logistic noise and variances 0.05, 0.5 and 15. Table (19) to (27) contains the results.

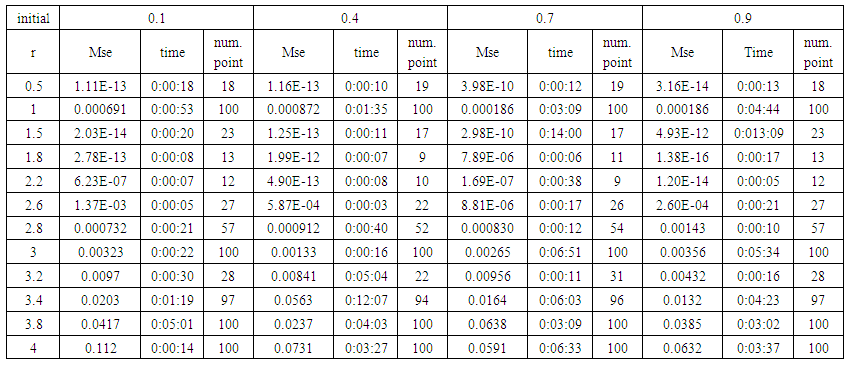Table (19). Time and MSE of approximate solution after many training trials with logistic noise by using logsig transfer function when the variance equal to 0.05

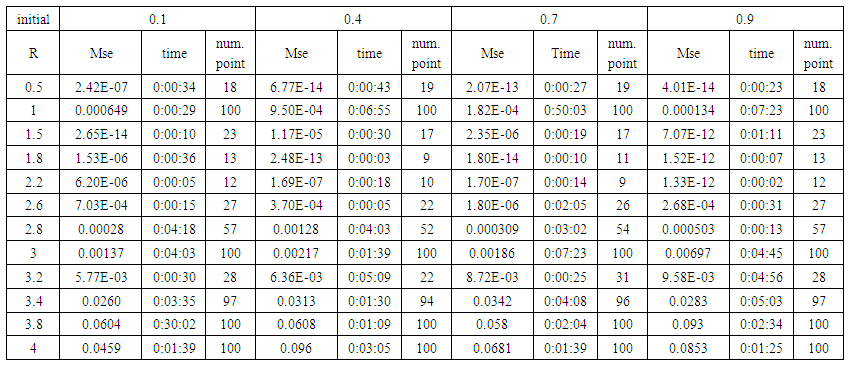Table (20). Time and MSE of approximate solution after many training trials with logistic noise by using tansig transfer function when the variance equal to 0.05

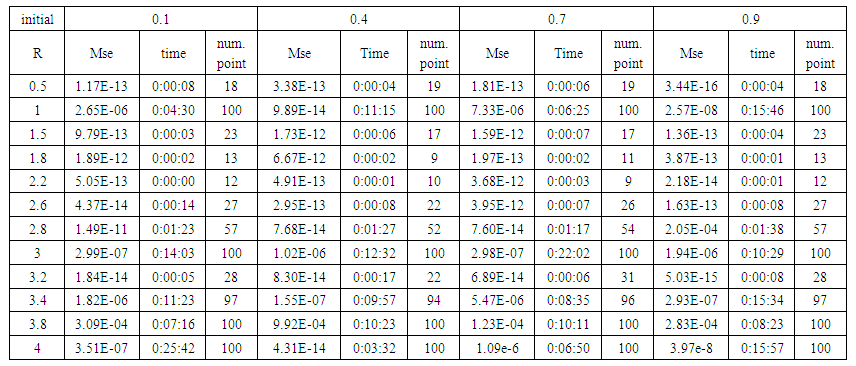Table (21). Time and MSE of approximate solution after many training trials with logistic noise by using FFT transfer function when the variance equal to 0.05

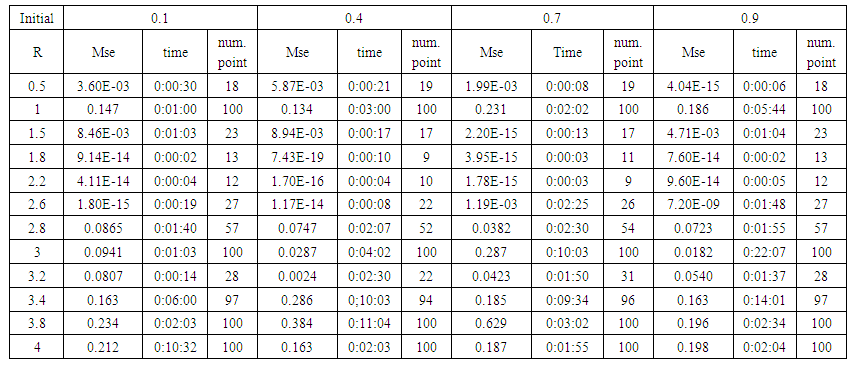Table (22). Time and MSE of approximate solution after many training trials with logistic noise by using logsig transfer function when the variance equal to 0.5

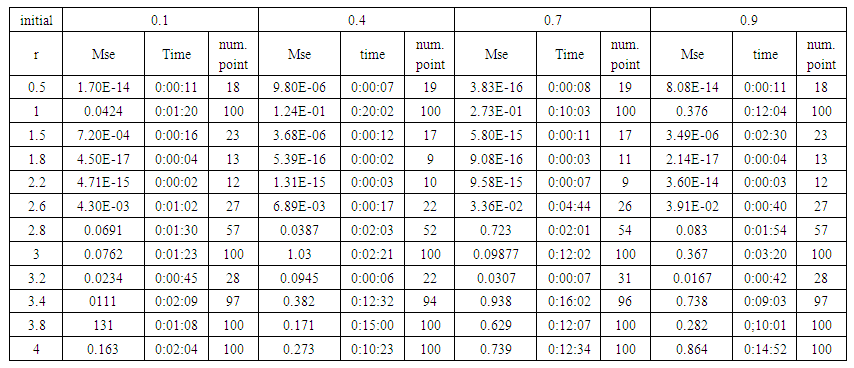Table (23). Time and MSE of approximate solution after many training trials with logistic noise by using tansig transfer function when the variance equal to 0.5

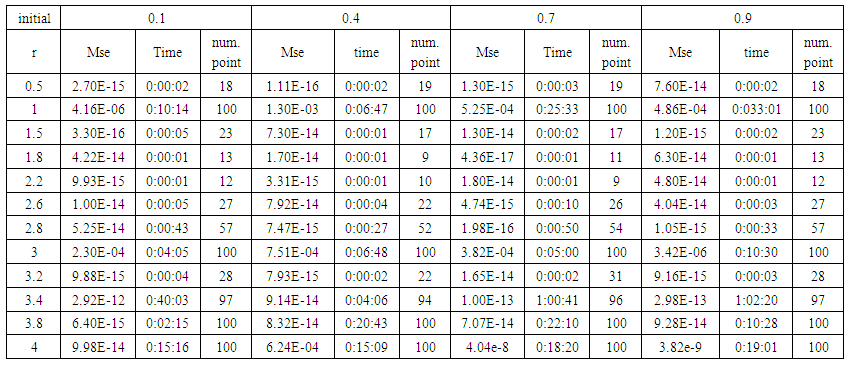Table (24). Time and MSE of approximate solution after many training trials with logistic noise by using FFT transfer function when the variance equal to 0.5

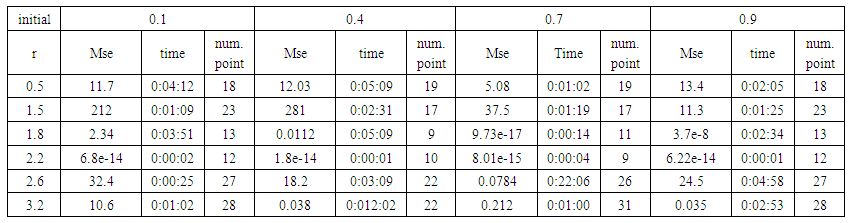Table (25). Time and MSE of approximate solution after many training trials with logistic noise by using logsig transfer function when the variance equal to 15

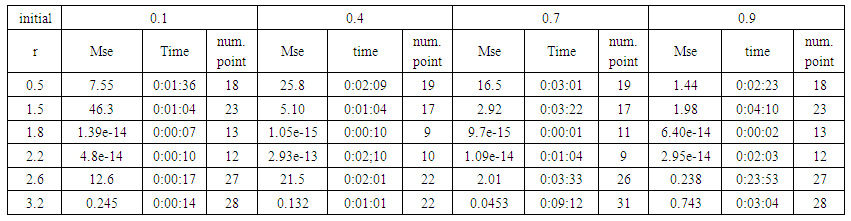Table (26). Time and MSE of approximate solution after many training trials with logistic noise by using tansig transfer function when the variance equal to 15

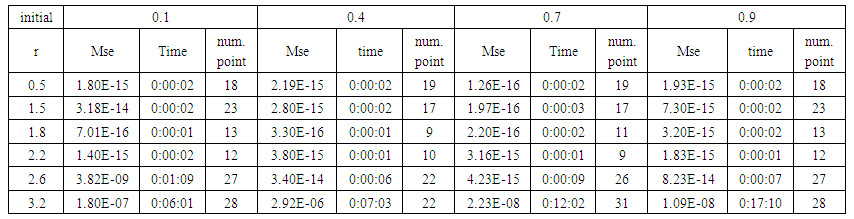Table (27). Time and MSE of approximate solution after many training trials with logistic noise by using FFT transfer function when the variance equal to 15

4.8. Results Discussion

From the above results it is clear that when the noises uniforme, normal and logistic with variances (0.05,0.5) the propose network FFNN side by side transfer function FFT has the best performance when the logistic map (deterministic, chaotic and high chaotic) but the performance function for the tansig and logsig transfer functions when the logistic map in deterministic and chaotic is good performance, in high chaotic the performance function for this transfer functions have a bad performance.

When the noises have variance 15 we trained the data for logistic map in cases deterministic and chaotic. We get the FFT transfer function has the best performance other than the tansig and logsig transfer functions have bad performance.

5. Summary

From the tables of results, it is clear when the noise is uniforme, normal and logistic with all considered variances values, that the FFT transfer function is the best among all other transfer functions in deterministic, chaotic and high chaotic cases.

The tansig and logsig transfer functions have good performance in deterministic and chaotic cases, but bad performance in high chaotic case. The other transfer functions have bad performance to estimate noisy logistic dynamical map.

The performance is measured by MSE criterion as we mentioned earlier.

The estimation of dynamical maps with noise obtained by trained Ann's offer some advantages, such as:

1- Complexity of computations increases with the increase of the number of sampling points in noisy Logistic dynamical map with noise.

2- The FFNNs with FFT transfer function provides a solution with noises (uniform, normal and logistic distributions) with very good performance function in compare with other traditional transfer functions.

3- The proposed FFNNs with FFT transfer function can be applied to one deamination dynamical maps with noise.

4- The proposed transfer function FFT gave best rustles specially when the logistic dynamical map with noises (uniform, normal, logistic distributions).

5- The proposed transfer function FFT is faster other than other traditional transfer functions in most cases of dynamical maps one deamination with noises with noises (uniform, normal and logistic distributions).

6- In general, the experimental results show that the FFNN side by side FFT transfer function which proposed can handle effectively noisy logistic dynamical map and provide accurate approximate solution throughout the whole domain, because three points the first point neural network computations is parallel the second point FFT analysis of data and computations are parallel and third point FFT transfer function returns differences in data to sources original related homogeneity data and sectors of the work.

7- The new transfer function FFT has ability on break up between chaotic and noise in Logistic dynamical map.

Some future works can be recommended. These works is as follows

1- Using networks with three or more hidden layers.

2- Increase the neurons in each hidden layer.

3- Use other random variables as noise.

4- Estimate multidimensional dynamical maps.

5- We recommended using FFT as transfer function in practical application.