J. A. Ugboh, I. M. Esuabana
Department of Mathematics, University of Calabar, Calabar, Cross River State, Nigeria
Correspondence to: I. M. Esuabana, Department of Mathematics, University of Calabar, Calabar, Cross River State, Nigeria.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
A new method for finding approximate roots (one at a time) of Nonlinear Algebraic or Transcendental Equations is developed similar in form with the bisection method. Given such an equation say, 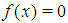 , with a root, say
, with a root, say 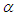 on the interval
on the interval 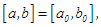 or the succeeding interval
or the succeeding interval 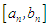 is partitioned into ten equal subintervals. The function is then evaluated at the mid-point
is partitioned into ten equal subintervals. The function is then evaluated at the mid-point 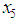 and compared with
and compared with 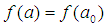 or with
or with 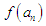 for the nthiteration. If
for the nthiteration. If 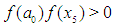 or
or  , the root is to the right of
, the root is to the right of 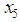 otherwise it is to its left. A search is then conducted to determine which of the remaining five subintervals contains the root. The midpoint of such an interval is the approximate root
otherwise it is to its left. A search is then conducted to determine which of the remaining five subintervals contains the root. The midpoint of such an interval is the approximate root 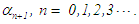 After the nth iteration, the approximate root
After the nth iteration, the approximate root 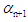 is the midpoint of the interval whose length is
is the midpoint of the interval whose length is 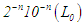 ; where
; where 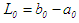 and
and 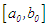 is the initial interval. A theorem that gurantees the convergence of the approximate roots to the actual root was stated and proved. Half the length of the succeeding interval
is the initial interval. A theorem that gurantees the convergence of the approximate roots to the actual root was stated and proved. Half the length of the succeeding interval 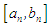 serves as upper bound for the error in the approximation. An algorithm was developed and a program coded in JAVA was used to solve seven test problems. The results show that the method yielded approximations which are all correct to ten decimal places after ten iterations; and correct to fifteen decimal places after fifteen or fourteen iterations.
serves as upper bound for the error in the approximation. An algorithm was developed and a program coded in JAVA was used to solve seven test problems. The results show that the method yielded approximations which are all correct to ten decimal places after ten iterations; and correct to fifteen decimal places after fifteen or fourteen iterations.
Keywords:
Nonlinear, Algebraic, Transcendental, Equations, Roots, Iterations, Approximations, Errors
Cite this paper: J. A. Ugboh, I. M. Esuabana, Marching Method: A New Numerical Method for Finding Roots of Algebraic and Transcendental Equations, American Journal of Computational and Applied Mathematics , Vol. 9 No. 1, 2019, pp. 6-11. doi: 10.5923/j.ajcam.20190901.02.
1. Introduction
Given a non linear algebraic or transcendental equation of the form: 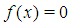 ; one often resort to numerical methods where analytic solution are not easy to come by. A good number of such methods are available and one of the simplest is the bisection method. However, the rate of convergence for the bisection method is very slow and so not suitable in a situation where high precision is required. It is therefore necessary to search for a method that is as simple but yeild highly accurate results in a few number of iterations. In this work, we present a method that is simple with high precision in a few number of iterations, machine implementable and guarantee convergence to desired root.The marching method involves partitioning the given interval
; one often resort to numerical methods where analytic solution are not easy to come by. A good number of such methods are available and one of the simplest is the bisection method. However, the rate of convergence for the bisection method is very slow and so not suitable in a situation where high precision is required. It is therefore necessary to search for a method that is as simple but yeild highly accurate results in a few number of iterations. In this work, we present a method that is simple with high precision in a few number of iterations, machine implementable and guarantee convergence to desired root.The marching method involves partitioning the given interval 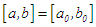 , or the succeeding interval
, or the succeeding interval 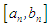 into ten subintervals of equal size with
into ten subintervals of equal size with 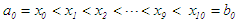 or
or 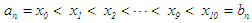 ; one of which must contain the root or one of the end points must be the root. For succeeding intervals
; one of which must contain the root or one of the end points must be the root. For succeeding intervals 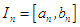 at the nth iteration, the lower and upper end points becomes respectively
at the nth iteration, the lower and upper end points becomes respectively 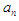 and
and 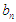 A search is conducted from the midpoint
A search is conducted from the midpoint 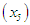 of the interval either to the left or right to determine the subinterval which contains the root. Given
of the interval either to the left or right to determine the subinterval which contains the root. Given 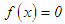 on
on 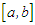 with
with 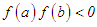 , and midpoint
, and midpoint 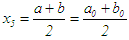 in the first iteration; (or
in the first iteration; (or 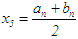 for the nth iteration); the following decision rule applies: if
for the nth iteration); the following decision rule applies: if 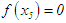 , the root is
, the root is 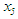 and we stop; otherwise, we search to the right of the midpoint if
and we stop; otherwise, we search to the right of the midpoint if 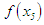 has same sign as
has same sign as 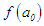 or
or 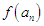 ; and to the left otherwise. In either case, a maximum of four searches is required. It is worthy of note that the search might just be once!Once the subinterval,
; and to the left otherwise. In either case, a maximum of four searches is required. It is worthy of note that the search might just be once!Once the subinterval, 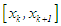 or
or 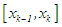 containing the root is found, the approximate root
containing the root is found, the approximate root 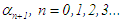 is taken as the midpoint of that subinterval leading to a succeeding interval
is taken as the midpoint of that subinterval leading to a succeeding interval 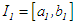 of length
of length 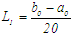 or
or 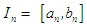 of length
of length 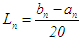 . Thus, in the first iteration, an upper bound for the error in approximation is
. Thus, in the first iteration, an upper bound for the error in approximation is 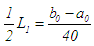 . After n iterations, the upper bound for the error is expected to be half of the length
. After n iterations, the upper bound for the error is expected to be half of the length 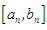 , that is, the error bound after n iterations is
, that is, the error bound after n iterations is 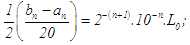 where
where 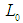 is the length of the starting interval. It is simple, machine implementable (can be coded in many high level languages), converges very fast to desired root and conserve space. However, it is a bit more difficult when compared to the bisection method due to the search. In any case, with high precision computers, the very high rate of convergence compensates for the extra work. An algorithm and a model software program in JAVA will be developed for the method. Seven test problems have been earmark for machine solution.
is the length of the starting interval. It is simple, machine implementable (can be coded in many high level languages), converges very fast to desired root and conserve space. However, it is a bit more difficult when compared to the bisection method due to the search. In any case, with high precision computers, the very high rate of convergence compensates for the extra work. An algorithm and a model software program in JAVA will be developed for the method. Seven test problems have been earmark for machine solution.
2. Preliminaries
A number of methods have been developed to solve nonlinear algebraic and/or transcendental equations of the form 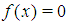 . The bisection method, secant method, Newton-Raphson method, regular falsi method and the general iteration technique are among the most commonly used ([1], [5], [7]). Slow convergence is one of the major drawbacks of most of these methods (except for Newton-Raphson). Newton- Raphson method though converges fast, has the flaw of requiring existence of first derivative and evaluation of two functional values per step ([3], [5], [6]]. Nonlinear equations have become indispensible tools among scientist in various disciplines hence, faster methods of solutions are in high demand. With the advent of high speed/precision computers and sophistication in proggamming, new methods of solutions are emerging. The efficiency, consistency, simplicity and economy of such a method are the measuring indexes ([6], [8], [4]). Lemma 2.1 Let
. The bisection method, secant method, Newton-Raphson method, regular falsi method and the general iteration technique are among the most commonly used ([1], [5], [7]). Slow convergence is one of the major drawbacks of most of these methods (except for Newton-Raphson). Newton- Raphson method though converges fast, has the flaw of requiring existence of first derivative and evaluation of two functional values per step ([3], [5], [6]]. Nonlinear equations have become indispensible tools among scientist in various disciplines hence, faster methods of solutions are in high demand. With the advent of high speed/precision computers and sophistication in proggamming, new methods of solutions are emerging. The efficiency, consistency, simplicity and economy of such a method are the measuring indexes ([6], [8], [4]). Lemma 2.1 Let 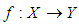 be any given real-valued function continuous on the closed and bounded interval
be any given real-valued function continuous on the closed and bounded interval 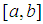 such that
such that 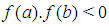 ; then there exists at least
; then there exists at least 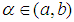 such that
such that 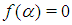 . [3], [2], [6]The above theorem, a consequence of intermediate value theorem, enables us determine interval where a root of the equation
. [3], [2], [6]The above theorem, a consequence of intermediate value theorem, enables us determine interval where a root of the equation 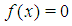 exists. However, if the function is highly oscillatory, there is a possibility of several roots in that interval. In other to avert this, the end points are taken close enough or a rough graph of
exists. However, if the function is highly oscillatory, there is a possibility of several roots in that interval. In other to avert this, the end points are taken close enough or a rough graph of 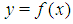 may be sketched to determine a rough point where the curve crosses the
may be sketched to determine a rough point where the curve crosses the 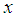 axis.
axis.
3. Methodology
Suppose we desire to find the root of the algebraic or transcendental equation say, 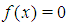 on the closed interval
on the closed interval 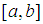 where
where 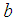 and
and 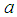 are close enough to avoid the existence of more than one root of
are close enough to avoid the existence of more than one root of 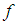 . The marching method involves the following steps.Step (i) Evaluate
. The marching method involves the following steps.Step (i) Evaluate 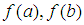 and confirm that
and confirm that 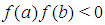 . Set
. Set 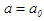 and
and 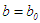 and error level
and error level 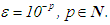 Step (ii) Partition the interval
Step (ii) Partition the interval 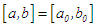 (or the succeeding interval
(or the succeeding interval 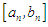 ) into ten equal parts with
) into ten equal parts with 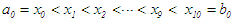 or
or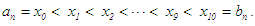 In the first iteration we take
In the first iteration we take 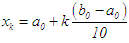 , where k = 0, 1, 2 · · · 10.In general, we take
, where k = 0, 1, 2 · · · 10.In general, we take 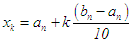 for the nth iteration, where k = 0, 1, 2 · · · 10 and n = 0, 1, 2, 3, · · · Step (iii): Conducting the search. Evaluate
for the nth iteration, where k = 0, 1, 2 · · · 10 and n = 0, 1, 2, 3, · · · Step (iii): Conducting the search. Evaluate 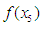 , if it is equal to zero you have the root, or
, if it is equal to zero you have the root, or 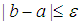 , stop, desired root is
, stop, desired root is 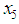 ; otherwise if it has the same sign as
; otherwise if it has the same sign as 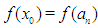 then the search is to the right of
then the search is to the right of 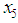 , and if of opposite sign, the search is to the left of
, and if of opposite sign, the search is to the left of 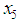 . The search is conducted as follows:(a) Suppose
. The search is conducted as follows:(a) Suppose 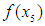 and
and 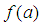 have the same sign, we evaluate
have the same sign, we evaluate 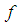 at
at 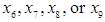 and for any k = 6, 7, 8 or 9 which
and for any k = 6, 7, 8 or 9 which 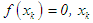 is the root, otherwise,if
is the root, otherwise,if 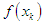 has opposite sign with
has opposite sign with 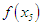 ; we have found the interval containing the root to be:
; we have found the interval containing the root to be: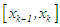 , if not, the last interval which is
, if not, the last interval which is 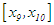 must contain the root. The approximate root is then:
must contain the root. The approximate root is then: 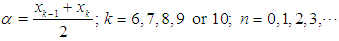 | (1) |
End points of new interval: Next evaluate 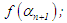 if
if 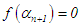 or
or 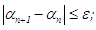 n = 0, 1, 2, 3 · · · or n = N maximum number of iterations, the root is
n = 0, 1, 2, 3 · · · or n = N maximum number of iterations, the root is 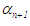 , stop, else, if
, stop, else, if 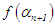 has same sign with
has same sign with 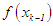 then
then 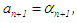 and
and 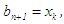 otherwise,
otherwise, 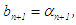 and
and 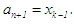 New or succeeding interval
New or succeeding interval 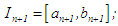 go to step (ii). (b) On the other hand, if
go to step (ii). (b) On the other hand, if 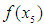 and
and 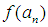 have opposite signs, we search to the left of
have opposite signs, we search to the left of 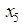 by evaluating
by evaluating 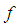 at
at 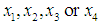 . For
. For 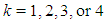 ; should
; should 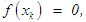 we have the root as
we have the root as 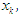 otherwise if
otherwise if 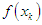 has same sign as
has same sign as 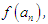 then the interval
then the interval 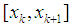 contains the root. Where none of these function values has same sign as
contains the root. Where none of these function values has same sign as 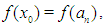 then the root must be in the first interval
then the root must be in the first interval 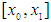 . The approximate root is then:
. The approximate root is then: 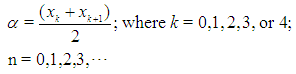 | (2) |
End points of new interval: Next evaluate 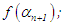 if
if 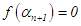 or
or 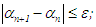 n = 0, 1, 2, 3 · · · or n = N maximum number of iterations, the root is
n = 0, 1, 2, 3 · · · or n = N maximum number of iterations, the root is 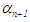 , stop, else, if
, stop, else, if 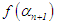 has same sign with
has same sign with 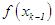 then
then 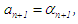 and
and 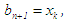 otherwise,
otherwise, 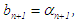 and
and 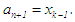 New or succeeding interval
New or succeeding interval 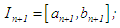 go to step (ii).(c) In summary, at any new iteration level we have the points of partition:
go to step (ii).(c) In summary, at any new iteration level we have the points of partition: 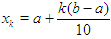 ; where
; where 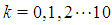 . The midpoint of the interval
. The midpoint of the interval 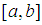 is always
is always 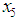 . The approximate root is:
. The approximate root is:  | (3) |
where 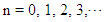 New Interval: Next evaluate
New Interval: Next evaluate 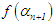 and if zero you have the root, otherwise, If the search was to the left of
and if zero you have the root, otherwise, If the search was to the left of 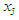 and
and 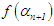 has same sign with
has same sign with 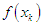 then
then 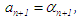 and
and 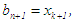 else,
else, 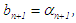 and
and 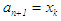 ; go to step (ii).If the search was to the right of
; go to step (ii).If the search was to the right of 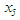 and
and 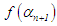 has same sign with
has same sign with 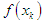 then
then 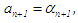 and
and 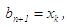 otherwise,
otherwise, 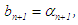 and
and 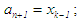 go to step (ii). The processes in steps (ii) to (iii) and (a) or (b) is continued until we have:
go to step (ii). The processes in steps (ii) to (iii) and (a) or (b) is continued until we have: 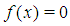 or
or 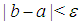 or after the desired number of iterations; where
or after the desired number of iterations; where 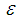 is the tolerable error.In all, seven test problems will be solved comprising of four polynomials and three transcendentals. Theorem 3.1 Let
is the tolerable error.In all, seven test problems will be solved comprising of four polynomials and three transcendentals. Theorem 3.1 Let 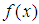 be any function continuous at all points of the interval
be any function continuous at all points of the interval 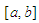 with
with 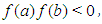 then the iteration
then the iteration 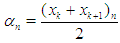 or
or 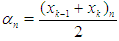 conerges to the root
conerges to the root 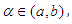 where
where 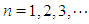 Proof.
Proof. 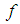 is continuous on the bounded interval
is continuous on the bounded interval 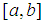 so with
so with 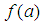 and
and 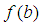 having opposite signs, we have a root
having opposite signs, we have a root 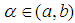 by theorem 2.1 . For the first iteration, the interval containing the root is of length
by theorem 2.1 . For the first iteration, the interval containing the root is of length 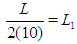 ; where L is the initial or starting length;
; where L is the initial or starting length; 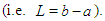 To obtain the next interval containing the root, the above interval is partioned into ten and the mid point of the new subinterval containing the root is used as the next approximation. Thus, the length of the second interval is
To obtain the next interval containing the root, the above interval is partioned into ten and the mid point of the new subinterval containing the root is used as the next approximation. Thus, the length of the second interval is 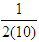 of
of 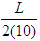 giving the length
giving the length 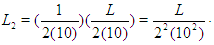 Continuing in this manner, at the
Continuing in this manner, at the 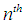 iteration, the length of the interval containing the root will be
iteration, the length of the interval containing the root will be 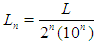 . As
. As 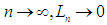 meaning that
meaning that 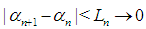 . Since
. Since 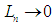 and the root
and the root 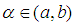 with
with 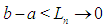 ;
; 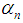 must converge to the root
must converge to the root 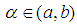 .
.
3.1. Algorithm
 CONDITIONF FOR ITERATION:
CONDITIONF FOR ITERATION: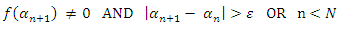
3.2. Comparative Analysis of Steps/Error
The method is about a modification of the well known bisection method. In each iteration step, the marching method partition the given interval 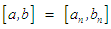 into ten sub intervals, evaluate functioal value of the mid point and at most four others, [but could be only one] (to its left or right) which it compare with that of the lower limit
into ten sub intervals, evaluate functioal value of the mid point and at most four others, [but could be only one] (to its left or right) which it compare with that of the lower limit 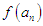 With the excution of each step the length of the succeeding interval is reduced to
With the excution of each step the length of the succeeding interval is reduced to 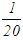 of the previous interval
of the previous interval 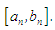 At the end of each step condition for succeeding interval which is excatly as in the bisection method is implimented. On the other hand, in the bisection method, the interval is halfed per each iterative step, mid point functional value compared with one of the end points
At the end of each step condition for succeeding interval which is excatly as in the bisection method is implimented. On the other hand, in the bisection method, the interval is halfed per each iterative step, mid point functional value compared with one of the end points 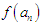 or
or 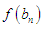 in each iteration step. At each of the step succeeding interval conditions are also implimented.Four steps in the bisection method can reduce the length of the interval
in each iteration step. At each of the step succeeding interval conditions are also implimented.Four steps in the bisection method can reduce the length of the interval 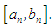 by a factor of
by a factor of 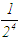 .To surpass the accuracy level of the marching method, five iterations of the bisection method will be required. From the search algorithm for the marching method, with one, two or three searches per step, the matching method will involve less work and post more accurate results, [i,e, 75 percent of the time]. After n iterations the length of the succeeding interval for the bisection method is:
.To surpass the accuracy level of the marching method, five iterations of the bisection method will be required. From the search algorithm for the marching method, with one, two or three searches per step, the matching method will involve less work and post more accurate results, [i,e, 75 percent of the time]. After n iterations the length of the succeeding interval for the bisection method is: 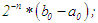 while that of the marching method is:
while that of the marching method is: 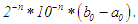 If that of the bisection is further divided by 8, we still have:
If that of the bisection is further divided by 8, we still have: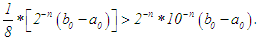 Error: Like in other brackecting methods, the maximum absolute error in the marching method is half the length of the nth interval. Thus after n iterations, the maximum absolute error in the method is:
Error: Like in other brackecting methods, the maximum absolute error in the marching method is half the length of the nth interval. Thus after n iterations, the maximum absolute error in the method is: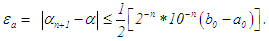 The convergence rate is linear. If we use the maximum or upper bound for the error at the nth iteration and denote it by
The convergence rate is linear. If we use the maximum or upper bound for the error at the nth iteration and denote it by 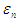 then we have (Chapra and Canale, 2006, Mathews, 1987)
then we have (Chapra and Canale, 2006, Mathews, 1987)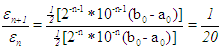
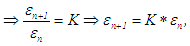 where
where  is a constant, hence the convergence is linear. For the bisection method the constant
is a constant, hence the convergence is linear. For the bisection method the constant 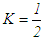 . It follows that the bisection method redues the bracketing interval by half while the marching method reduces same interval by a factor of 20.
. It follows that the bisection method redues the bracketing interval by half while the marching method reduces same interval by a factor of 20.
4. Results
The following test problems were solved with the marching method using a program coded in JAVA.Problem 1: Use the matching method to find the root of 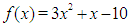 in
in 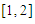 ; using the first 15 iterations. Out put the successive intervals and the approximate root in each interval.
; using the first 15 iterations. Out put the successive intervals and the approximate root in each interval.Table 1. Results showing approximate roots of
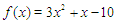 in in
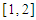 ; obtained from a JAVA coding ; obtained from a JAVA coding
 |
| |
|
Root = 1.6666666666666667. Observe that the root is correct to 10 decimal places at the 10th iteration and to 15 decimal places at the 15th. The exact root is 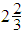 .Problem 2: Use the matching method to find the root of
.Problem 2: Use the matching method to find the root of 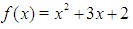 in
in 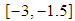 ; using the first 14 iterations. Output the successive intervals and the approximate root in each interval.
; using the first 14 iterations. Output the successive intervals and the approximate root in each interval.Table 2. Results showing approximate roots of
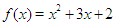 in in
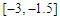 obtained from a JAVA coding obtained from a JAVA coding
 |
| |
|
Root = -2.000000000000001. The exact root in this interval is - 2. Observe that the root is correct to 10 decimal places with the 10th iteration and to 15 decimal places at the 15th.Problem 3: By using the marching method, obtain an approximate root of 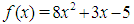 in
in 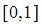 using the first 15 iterations. Out put the successive intervals and the approximate root in each interval.
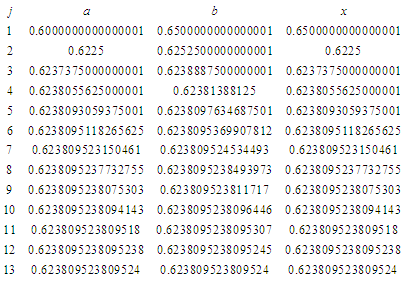
using the first 15 iterations. Out put the successive intervals and the approximate root in each interval. Table 3. Results showing approximate roots of
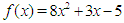 in in
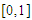 ; obtained from a JAVA coding ; obtained from a JAVA coding
 |
| |
|
Root = 0.623809523809524. From the 13th iteration the root is correct to 15 decimal places! Excat root unknown but is in 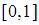 .Problem 4: By using the marching method obtain an approximate root for
.Problem 4: By using the marching method obtain an approximate root for 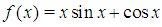 in
in 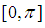 ;
; 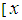 in radians] using the first 15 iterations. Output end points of successive interval and the approximate roots in each interval.
in radians] using the first 15 iterations. Output end points of successive interval and the approximate roots in each interval.Table 4. Results showing approximate roots of
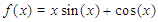 on on
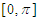 ; obtained from coding in JAVA ; obtained from coding in JAVA
 |
| |
|
Root = 2.7983199854750005 correct to 15 decimal places after 14 iterations. Excat root not known.Problem 5: Obtain an approximate root of 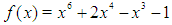 on
on 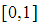 ; with the marching method using the first 15 iterations. Out put the end points of successive intervals and the approximate root in each.
; with the marching method using the first 15 iterations. Out put the end points of successive intervals and the approximate root in each. Table 5. Results showing approximate roots of
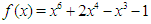 on on
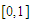 ; obtained from a JAVA coding ; obtained from a JAVA coding
 |
| |
|
Root = 0.8827887463817081 which is correct to 15 decimal places at the 15th iteration. Exact root not known.Problem 6: Determine the approximate root of 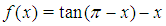 on the interval
on the interval 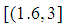 where
where 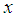 is in radians with the first 16 iterations.
is in radians with the first 16 iterations.Table 6. Results showing approximate roots of
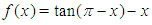 on on
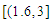 ; obtained from a JAVA coding ; obtained from a JAVA coding
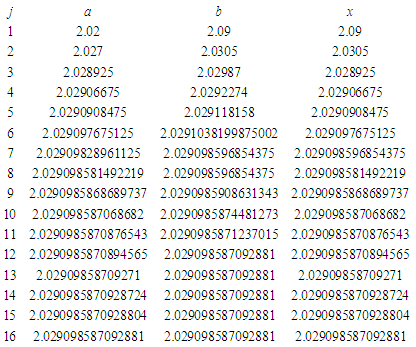 |
| |
|
Root = 2.029098587092881 after 16 iterations. Exact root not known but in 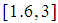 .Problem 7: Determine the approximate root of
.Problem 7: Determine the approximate root of 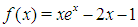 on the interval
on the interval 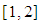 correct to 15 decimal places or using the first 15 iterations of the marching method.
correct to 15 decimal places or using the first 15 iterations of the marching method.Table 7. Results showing approximate roots of
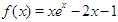 on on
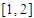 ; obtained from a JAVA coding ; obtained from a JAVA coding
 |
| |
|
Root = 1.0750365345312498 correct to 15 decimal places after 14 iterations. Exact root in 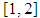 is not known.
is not known.
5. Conclusions
The matching method is designed to determine a root of nonlinear equation at a time. Given that a root exists on the interval 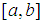 , i.e.
, i.e. 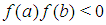 , the interval is partitioned into ten equal parts with
, the interval is partitioned into ten equal parts with 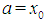 and
and 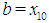 . Either one of the end points of the subintervals is the root or one of the subintervals contains the root. A search is conducted to determine this interval. This search might involve evaluation of at most four functional values or might just be one or two per step! The approximate root is taken as the mid-point of the new interval and if it is not the root, the process is repeated until the root is found or the stopping criterion is met. An algorithm was developed and a program coded in JAVA was used to solve seven test problems involving polynomials and transcendental functions. Results are tabulated the tables give the intervals and the approximate roots for each step. Results obtained show a very high precision of about ten decimal places in ten iterations which is equivalent to one decimal per step. For few decimal places or iterations, computation with calculator can be used.The Marching Method ensures that the approximation converges to the desired root, highly accurate, economical in terms of space and time, easy to program and can be used to solve nonlinear algebraic or transcendental equations. The program coding can be done in any other high level language that is capable of searching.
. Either one of the end points of the subintervals is the root or one of the subintervals contains the root. A search is conducted to determine this interval. This search might involve evaluation of at most four functional values or might just be one or two per step! The approximate root is taken as the mid-point of the new interval and if it is not the root, the process is repeated until the root is found or the stopping criterion is met. An algorithm was developed and a program coded in JAVA was used to solve seven test problems involving polynomials and transcendental functions. Results are tabulated the tables give the intervals and the approximate roots for each step. Results obtained show a very high precision of about ten decimal places in ten iterations which is equivalent to one decimal per step. For few decimal places or iterations, computation with calculator can be used.The Marching Method ensures that the approximation converges to the desired root, highly accurate, economical in terms of space and time, easy to program and can be used to solve nonlinear algebraic or transcendental equations. The program coding can be done in any other high level language that is capable of searching.
References
| [1] | Ele, B. I. and Ugboh, J. A.. Numerical Computations for Science and Engineering with C++ Programming Basics. Radiant Ventures Press, Calabar – Nigeria, 2017. |
| [2] | Gaughan, E. G., Introduction to Analysis. Brooks/Cole Publishing company, California, 1993. |
| [3] | Grewal, B. S., Numerical Methods in Engineering and Science. Khanna Publishers, Delhi, 1997. |
| [4] | Haeussler, E. F., Paul, R. S., and Wood, R. J., Introductory Mathematical Analysis for Business, Economics, and Life and Social Sciences. Printice-Hall, Boston, 2011. |
| [5] | Mathews, J. H., Numerical Methods for Computer Science, Engineering and Mathematics, Printice-Hall, New Jersey, 1987. |
| [6] | Olayi, G. A., Introduction to Numerical Analysis. ABU Press, Zaria – Nigeria, 2000. |
| [7] | Riley, K. F., P., H. M., and Bence, S. J., Mathematical Methods for Physics and Engineering, Cambridge University Press, United Kingdom, 1998. |
| [8] | Won, Y. Y., Applied Numerical Methods Using MATLAB, John Wiley Interscience, New York, 2005. |


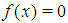 , with a root, say
, with a root, say 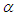 on the interval
on the interval 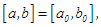 or the succeeding interval
or the succeeding interval 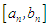 is partitioned into ten equal subintervals. The function is then evaluated at the mid-point
is partitioned into ten equal subintervals. The function is then evaluated at the mid-point 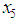 and compared with
and compared with 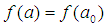 or with
or with 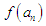 for the nthiteration. If
for the nthiteration. If 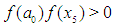 or
or  , the root is to the right of
, the root is to the right of 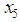 otherwise it is to its left. A search is then conducted to determine which of the remaining five subintervals contains the root. The midpoint of such an interval is the approximate root
otherwise it is to its left. A search is then conducted to determine which of the remaining five subintervals contains the root. The midpoint of such an interval is the approximate root 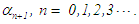 After the nth iteration, the approximate root
After the nth iteration, the approximate root 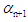 is the midpoint of the interval whose length is
is the midpoint of the interval whose length is 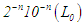 ; where
; where 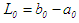 and
and 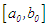 is the initial interval. A theorem that gurantees the convergence of the approximate roots to the actual root was stated and proved. Half the length of the succeeding interval
is the initial interval. A theorem that gurantees the convergence of the approximate roots to the actual root was stated and proved. Half the length of the succeeding interval 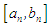 serves as upper bound for the error in the approximation. An algorithm was developed and a program coded in JAVA was used to solve seven test problems. The results show that the method yielded approximations which are all correct to ten decimal places after ten iterations; and correct to fifteen decimal places after fifteen or fourteen iterations.
serves as upper bound for the error in the approximation. An algorithm was developed and a program coded in JAVA was used to solve seven test problems. The results show that the method yielded approximations which are all correct to ten decimal places after ten iterations; and correct to fifteen decimal places after fifteen or fourteen iterations.
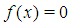 ; one often resort to numerical methods where analytic solution are not easy to come by. A good number of such methods are available and one of the simplest is the bisection method. However, the rate of convergence for the bisection method is very slow and so not suitable in a situation where high precision is required. It is therefore necessary to search for a method that is as simple but yeild highly accurate results in a few number of iterations. In this work, we present a method that is simple with high precision in a few number of iterations, machine implementable and guarantee convergence to desired root.The marching method involves partitioning the given interval
; one often resort to numerical methods where analytic solution are not easy to come by. A good number of such methods are available and one of the simplest is the bisection method. However, the rate of convergence for the bisection method is very slow and so not suitable in a situation where high precision is required. It is therefore necessary to search for a method that is as simple but yeild highly accurate results in a few number of iterations. In this work, we present a method that is simple with high precision in a few number of iterations, machine implementable and guarantee convergence to desired root.The marching method involves partitioning the given interval 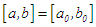 , or the succeeding interval
, or the succeeding interval 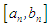 into ten subintervals of equal size with
into ten subintervals of equal size with 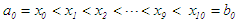 or
or 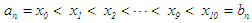 ; one of which must contain the root or one of the end points must be the root. For succeeding intervals
; one of which must contain the root or one of the end points must be the root. For succeeding intervals 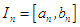 at the nth iteration, the lower and upper end points becomes respectively
at the nth iteration, the lower and upper end points becomes respectively 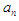 and
and 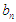 A search is conducted from the midpoint
A search is conducted from the midpoint 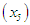 of the interval either to the left or right to determine the subinterval which contains the root. Given
of the interval either to the left or right to determine the subinterval which contains the root. Given 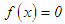 on
on 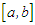 with
with 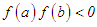 , and midpoint
, and midpoint 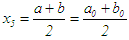 in the first iteration; (or
in the first iteration; (or 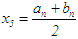 for the nth iteration); the following decision rule applies: if
for the nth iteration); the following decision rule applies: if 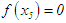 , the root is
, the root is 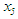 and we stop; otherwise, we search to the right of the midpoint if
and we stop; otherwise, we search to the right of the midpoint if 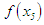 has same sign as
has same sign as 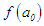 or
or 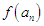 ; and to the left otherwise. In either case, a maximum of four searches is required. It is worthy of note that the search might just be once!Once the subinterval,
; and to the left otherwise. In either case, a maximum of four searches is required. It is worthy of note that the search might just be once!Once the subinterval, 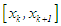 or
or 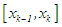 containing the root is found, the approximate root
containing the root is found, the approximate root 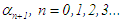 is taken as the midpoint of that subinterval leading to a succeeding interval
is taken as the midpoint of that subinterval leading to a succeeding interval 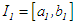 of length
of length 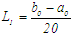 or
or 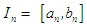 of length
of length 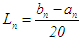 . Thus, in the first iteration, an upper bound for the error in approximation is
. Thus, in the first iteration, an upper bound for the error in approximation is 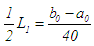 . After n iterations, the upper bound for the error is expected to be half of the length
. After n iterations, the upper bound for the error is expected to be half of the length 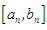 , that is, the error bound after n iterations is
, that is, the error bound after n iterations is 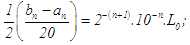 where
where 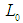 is the length of the starting interval. It is simple, machine implementable (can be coded in many high level languages), converges very fast to desired root and conserve space. However, it is a bit more difficult when compared to the bisection method due to the search. In any case, with high precision computers, the very high rate of convergence compensates for the extra work. An algorithm and a model software program in JAVA will be developed for the method. Seven test problems have been earmark for machine solution.
is the length of the starting interval. It is simple, machine implementable (can be coded in many high level languages), converges very fast to desired root and conserve space. However, it is a bit more difficult when compared to the bisection method due to the search. In any case, with high precision computers, the very high rate of convergence compensates for the extra work. An algorithm and a model software program in JAVA will be developed for the method. Seven test problems have been earmark for machine solution.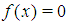 . The bisection method, secant method, Newton-Raphson method, regular falsi method and the general iteration technique are among the most commonly used ([1], [5], [7]). Slow convergence is one of the major drawbacks of most of these methods (except for Newton-Raphson). Newton- Raphson method though converges fast, has the flaw of requiring existence of first derivative and evaluation of two functional values per step ([3], [5], [6]]. Nonlinear equations have become indispensible tools among scientist in various disciplines hence, faster methods of solutions are in high demand. With the advent of high speed/precision computers and sophistication in proggamming, new methods of solutions are emerging. The efficiency, consistency, simplicity and economy of such a method are the measuring indexes ([6], [8], [4]). Lemma 2.1 Let
. The bisection method, secant method, Newton-Raphson method, regular falsi method and the general iteration technique are among the most commonly used ([1], [5], [7]). Slow convergence is one of the major drawbacks of most of these methods (except for Newton-Raphson). Newton- Raphson method though converges fast, has the flaw of requiring existence of first derivative and evaluation of two functional values per step ([3], [5], [6]]. Nonlinear equations have become indispensible tools among scientist in various disciplines hence, faster methods of solutions are in high demand. With the advent of high speed/precision computers and sophistication in proggamming, new methods of solutions are emerging. The efficiency, consistency, simplicity and economy of such a method are the measuring indexes ([6], [8], [4]). Lemma 2.1 Let 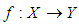 be any given real-valued function continuous on the closed and bounded interval
be any given real-valued function continuous on the closed and bounded interval 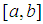 such that
such that 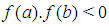 ; then there exists at least
; then there exists at least 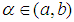 such that
such that 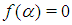 . [3], [2], [6]The above theorem, a consequence of intermediate value theorem, enables us determine interval where a root of the equation
. [3], [2], [6]The above theorem, a consequence of intermediate value theorem, enables us determine interval where a root of the equation 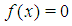 exists. However, if the function is highly oscillatory, there is a possibility of several roots in that interval. In other to avert this, the end points are taken close enough or a rough graph of
exists. However, if the function is highly oscillatory, there is a possibility of several roots in that interval. In other to avert this, the end points are taken close enough or a rough graph of 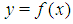 may be sketched to determine a rough point where the curve crosses the
may be sketched to determine a rough point where the curve crosses the  axis.
axis. 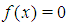 on the closed interval
on the closed interval 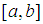 where
where 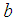 and
and 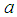 are close enough to avoid the existence of more than one root of
are close enough to avoid the existence of more than one root of 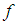 . The marching method involves the following steps.Step (i) Evaluate
. The marching method involves the following steps.Step (i) Evaluate 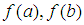 and confirm that
and confirm that 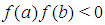 . Set
. Set 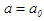 and
and 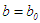 and error level
and error level 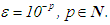 Step (ii) Partition the interval
Step (ii) Partition the interval 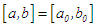 (or the succeeding interval
(or the succeeding interval 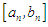 ) into ten equal parts with
) into ten equal parts with 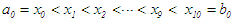 or
or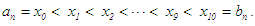 In the first iteration we take
In the first iteration we take 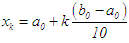 , where k = 0, 1, 2 · · · 10.In general, we take
, where k = 0, 1, 2 · · · 10.In general, we take 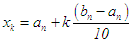 for the nth iteration, where k = 0, 1, 2 · · · 10 and n = 0, 1, 2, 3, · · · Step (iii): Conducting the search. Evaluate
for the nth iteration, where k = 0, 1, 2 · · · 10 and n = 0, 1, 2, 3, · · · Step (iii): Conducting the search. Evaluate 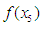 , if it is equal to zero you have the root, or
, if it is equal to zero you have the root, or 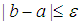 , stop, desired root is
, stop, desired root is 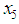 ; otherwise if it has the same sign as
; otherwise if it has the same sign as 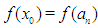 then the search is to the right of
then the search is to the right of 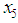 , and if of opposite sign, the search is to the left of
, and if of opposite sign, the search is to the left of 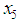 . The search is conducted as follows:(a) Suppose
. The search is conducted as follows:(a) Suppose 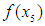 and
and 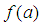 have the same sign, we evaluate
have the same sign, we evaluate 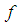 at
at 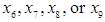 and for any k = 6, 7, 8 or 9 which
and for any k = 6, 7, 8 or 9 which 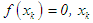 is the root, otherwise,if
is the root, otherwise,if 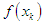 has opposite sign with
has opposite sign with 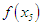 ; we have found the interval containing the root to be:
; we have found the interval containing the root to be: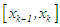 , if not, the last interval which is
, if not, the last interval which is 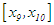 must contain the root. The approximate root is then:
must contain the root. The approximate root is then: 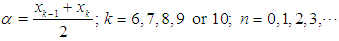
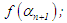 if
if 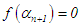 or
or 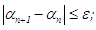 n = 0, 1, 2, 3 · · · or n = N maximum number of iterations, the root is
n = 0, 1, 2, 3 · · · or n = N maximum number of iterations, the root is 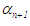 , stop, else, if
, stop, else, if 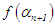 has same sign with
has same sign with 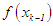 then
then 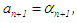 and
and 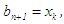 otherwise,
otherwise, 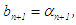 and
and 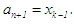 New or succeeding interval
New or succeeding interval 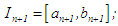 go to step (ii). (b) On the other hand, if
go to step (ii). (b) On the other hand, if 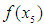 and
and 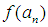 have opposite signs, we search to the left of
have opposite signs, we search to the left of 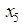 by evaluating
by evaluating 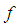 at
at 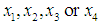 . For
. For 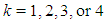 ; should
; should 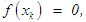 we have the root as
we have the root as 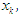 otherwise if
otherwise if 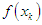 has same sign as
has same sign as 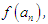 then the interval
then the interval 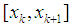 contains the root. Where none of these function values has same sign as
contains the root. Where none of these function values has same sign as 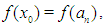 then the root must be in the first interval
then the root must be in the first interval 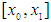 . The approximate root is then:
. The approximate root is then: 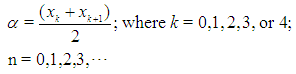
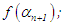 if
if 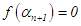 or
or 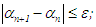 n = 0, 1, 2, 3 · · · or n = N maximum number of iterations, the root is
n = 0, 1, 2, 3 · · · or n = N maximum number of iterations, the root is 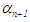 , stop, else, if
, stop, else, if 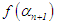 has same sign with
has same sign with 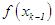 then
then 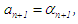 and
and 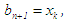 otherwise,
otherwise, 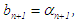 and
and 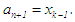 New or succeeding interval
New or succeeding interval 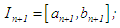 go to step (ii).(c) In summary, at any new iteration level we have the points of partition:
go to step (ii).(c) In summary, at any new iteration level we have the points of partition: 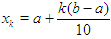 ; where
; where 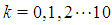 . The midpoint of the interval
. The midpoint of the interval 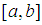 is always
is always 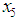 . The approximate root is:
. The approximate root is: 
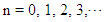 New Interval: Next evaluate
New Interval: Next evaluate 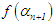 and if zero you have the root, otherwise, If the search was to the left of
and if zero you have the root, otherwise, If the search was to the left of 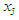 and
and 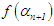 has same sign with
has same sign with 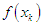 then
then 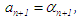 and
and 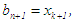 else,
else, 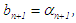 and
and 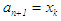 ; go to step (ii).If the search was to the right of
; go to step (ii).If the search was to the right of 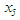 and
and 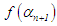 has same sign with
has same sign with 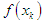 then
then 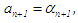 and
and 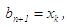 otherwise,
otherwise, 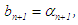 and
and 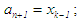 go to step (ii). The processes in steps (ii) to (iii) and (a) or (b) is continued until we have:
go to step (ii). The processes in steps (ii) to (iii) and (a) or (b) is continued until we have: 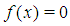 or
or 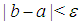 or after the desired number of iterations; where
or after the desired number of iterations; where 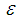 is the tolerable error.In all, seven test problems will be solved comprising of four polynomials and three transcendentals. Theorem 3.1 Let
is the tolerable error.In all, seven test problems will be solved comprising of four polynomials and three transcendentals. Theorem 3.1 Let 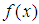 be any function continuous at all points of the interval
be any function continuous at all points of the interval 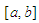 with
with 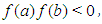 then the iteration
then the iteration 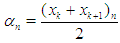 or
or 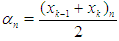 conerges to the root
conerges to the root 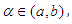 where
where 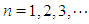 Proof.
Proof. 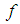 is continuous on the bounded interval
is continuous on the bounded interval 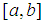 so with
so with 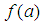 and
and 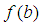 having opposite signs, we have a root
having opposite signs, we have a root 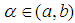 by theorem 2.1 . For the first iteration, the interval containing the root is of length
by theorem 2.1 . For the first iteration, the interval containing the root is of length 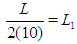 ; where L is the initial or starting length;
; where L is the initial or starting length; 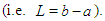 To obtain the next interval containing the root, the above interval is partioned into ten and the mid point of the new subinterval containing the root is used as the next approximation. Thus, the length of the second interval is
To obtain the next interval containing the root, the above interval is partioned into ten and the mid point of the new subinterval containing the root is used as the next approximation. Thus, the length of the second interval is 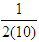 of
of 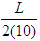 giving the length
giving the length 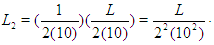 Continuing in this manner, at the
Continuing in this manner, at the 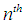 iteration, the length of the interval containing the root will be
iteration, the length of the interval containing the root will be 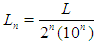 . As
. As 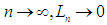 meaning that
meaning that 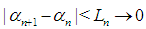 . Since
. Since 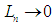 and the root
and the root 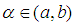 with
with 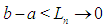 ;
; 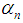 must converge to the root
must converge to the root 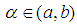 .
.  CONDITIONF FOR ITERATION:
CONDITIONF FOR ITERATION: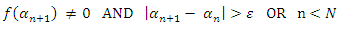
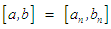 into ten sub intervals, evaluate functioal value of the mid point and at most four others, [but could be only one] (to its left or right) which it compare with that of the lower limit
into ten sub intervals, evaluate functioal value of the mid point and at most four others, [but could be only one] (to its left or right) which it compare with that of the lower limit 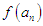 With the excution of each step the length of the succeeding interval is reduced to
With the excution of each step the length of the succeeding interval is reduced to 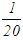 of the previous interval
of the previous interval 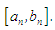 At the end of each step condition for succeeding interval which is excatly as in the bisection method is implimented. On the other hand, in the bisection method, the interval is halfed per each iterative step, mid point functional value compared with one of the end points
At the end of each step condition for succeeding interval which is excatly as in the bisection method is implimented. On the other hand, in the bisection method, the interval is halfed per each iterative step, mid point functional value compared with one of the end points 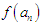 or
or 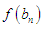 in each iteration step. At each of the step succeeding interval conditions are also implimented.Four steps in the bisection method can reduce the length of the interval
in each iteration step. At each of the step succeeding interval conditions are also implimented.Four steps in the bisection method can reduce the length of the interval 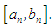 by a factor of
by a factor of 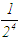 .To surpass the accuracy level of the marching method, five iterations of the bisection method will be required. From the search algorithm for the marching method, with one, two or three searches per step, the matching method will involve less work and post more accurate results, [i,e, 75 percent of the time]. After n iterations the length of the succeeding interval for the bisection method is:
.To surpass the accuracy level of the marching method, five iterations of the bisection method will be required. From the search algorithm for the marching method, with one, two or three searches per step, the matching method will involve less work and post more accurate results, [i,e, 75 percent of the time]. After n iterations the length of the succeeding interval for the bisection method is: 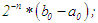 while that of the marching method is:
while that of the marching method is: 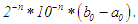 If that of the bisection is further divided by 8, we still have:
If that of the bisection is further divided by 8, we still have: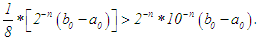 Error: Like in other brackecting methods, the maximum absolute error in the marching method is half the length of the nth interval. Thus after n iterations, the maximum absolute error in the method is:
Error: Like in other brackecting methods, the maximum absolute error in the marching method is half the length of the nth interval. Thus after n iterations, the maximum absolute error in the method is: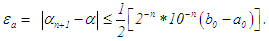 The convergence rate is linear. If we use the maximum or upper bound for the error at the nth iteration and denote it by
The convergence rate is linear. If we use the maximum or upper bound for the error at the nth iteration and denote it by 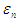 then we have (Chapra and Canale, 2006, Mathews, 1987)
then we have (Chapra and Canale, 2006, Mathews, 1987)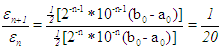
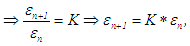 where
where  is a constant, hence the convergence is linear. For the bisection method the constant
is a constant, hence the convergence is linear. For the bisection method the constant 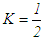 . It follows that the bisection method redues the bracketing interval by half while the marching method reduces same interval by a factor of 20.
. It follows that the bisection method redues the bracketing interval by half while the marching method reduces same interval by a factor of 20.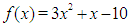 in
in 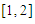 ; using the first 15 iterations. Out put the successive intervals and the approximate root in each interval.
; using the first 15 iterations. Out put the successive intervals and the approximate root in each interval.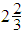 .Problem 2: Use the matching method to find the root of
.Problem 2: Use the matching method to find the root of 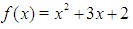 in
in 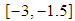 ; using the first 14 iterations. Output the successive intervals and the approximate root in each interval.
; using the first 14 iterations. Output the successive intervals and the approximate root in each interval.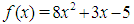 in
in 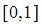 using the first 15 iterations. Out put the successive intervals and the approximate root in each interval.
using the first 15 iterations. Out put the successive intervals and the approximate root in each interval. 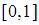 .Problem 4: By using the marching method obtain an approximate root for
.Problem 4: By using the marching method obtain an approximate root for 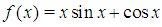 in
in 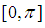 ;
; 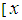 in radians] using the first 15 iterations. Output end points of successive interval and the approximate roots in each interval.
in radians] using the first 15 iterations. Output end points of successive interval and the approximate roots in each interval.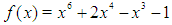 on
on 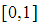 ; with the marching method using the first 15 iterations. Out put the end points of successive intervals and the approximate root in each.
; with the marching method using the first 15 iterations. Out put the end points of successive intervals and the approximate root in each. 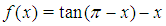 on the interval
on the interval 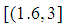 where
where 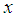 is in radians with the first 16 iterations.
is in radians with the first 16 iterations.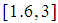 .Problem 7: Determine the approximate root of
.Problem 7: Determine the approximate root of 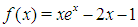 on the interval
on the interval 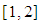 correct to 15 decimal places or using the first 15 iterations of the marching method.
correct to 15 decimal places or using the first 15 iterations of the marching method.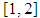 is not known.
is not known.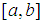 , i.e.
, i.e. 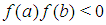 , the interval is partitioned into ten equal parts with
, the interval is partitioned into ten equal parts with 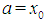 and
and 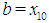 . Either one of the end points of the subintervals is the root or one of the subintervals contains the root. A search is conducted to determine this interval. This search might involve evaluation of at most four functional values or might just be one or two per step! The approximate root is taken as the mid-point of the new interval and if it is not the root, the process is repeated until the root is found or the stopping criterion is met. An algorithm was developed and a program coded in JAVA was used to solve seven test problems involving polynomials and transcendental functions. Results are tabulated the tables give the intervals and the approximate roots for each step. Results obtained show a very high precision of about ten decimal places in ten iterations which is equivalent to one decimal per step. For few decimal places or iterations, computation with calculator can be used.The Marching Method ensures that the approximation converges to the desired root, highly accurate, economical in terms of space and time, easy to program and can be used to solve nonlinear algebraic or transcendental equations. The program coding can be done in any other high level language that is capable of searching.
. Either one of the end points of the subintervals is the root or one of the subintervals contains the root. A search is conducted to determine this interval. This search might involve evaluation of at most four functional values or might just be one or two per step! The approximate root is taken as the mid-point of the new interval and if it is not the root, the process is repeated until the root is found or the stopping criterion is met. An algorithm was developed and a program coded in JAVA was used to solve seven test problems involving polynomials and transcendental functions. Results are tabulated the tables give the intervals and the approximate roots for each step. Results obtained show a very high precision of about ten decimal places in ten iterations which is equivalent to one decimal per step. For few decimal places or iterations, computation with calculator can be used.The Marching Method ensures that the approximation converges to the desired root, highly accurate, economical in terms of space and time, easy to program and can be used to solve nonlinear algebraic or transcendental equations. The program coding can be done in any other high level language that is capable of searching.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML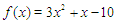 in
in 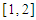 ; obtained from a JAVA coding
; obtained from a JAVA coding
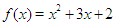 in
in 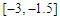 obtained from a JAVA coding
obtained from a JAVA coding
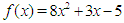 in
in 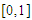 ; obtained from a JAVA coding
; obtained from a JAVA coding
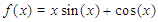 on
on 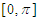 ; obtained from coding in JAVA
; obtained from coding in JAVA
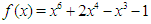 on
on 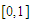 ; obtained from a JAVA coding
; obtained from a JAVA coding
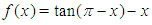 on
on 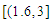 ; obtained from a JAVA coding
; obtained from a JAVA coding
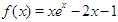 on
on 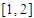 ; obtained from a JAVA coding
; obtained from a JAVA coding