1. Introduction

Volterra-Fredholm Integral equations have received significant meaning in the mathematical physics, biology, engineering, and contact problems in the theory of elasticity [14, 6]. These types of equations can be solved analytically in [1, 5]. At the same time, the sensing of numerical methods takes an important place in solving them [7, 15].

In the present work, we consider a mixed Volterra-Fredholm integral equation of the second kind of the form

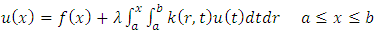(1)

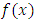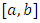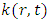we assume that is continuous on the interval and is continuous on 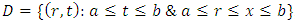, while u(x) is the unknown continuous function in 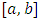to be determined.

Ahmed solved this equation by using least square approximation method, [12]. Wazwaz solved this problem by using the method of series solution and the Adomian decomposition method, [3]. In [10], Ezzati and Najafalizadeh used Cas wavelets for solving linear and nonlinear Volterra-Fredholm integral equations. In [9] Wang used least square approximation method to solve this type of equation. In addition, Ibrahim used new iterative method for solving the linear Volterra-Fredholm and mixed Volterra-Fredholm integral equations in [4]. Also, Hasan solved it by using linear programming method, [8].

The objective of this work is to study the existence and uniqueness of solution of equation (1), also to present an approximate solution using fixed point iteration method, and then the Aitken method is used to accelerate the convergence of the solution.

2. Definitions and Theores [11, 2]

This section deals with some definitions and theorems which are used in this work

Definition 2.1. Let 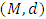be a metric space and 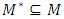with the mapping 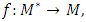an element 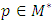is a fixed point of the mapping f if .

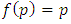Definition 2.2. Let 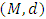be a complete metric space, the mapping 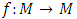is called contractive mapping if there is a real number 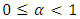such that for each 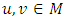we have

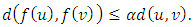Definition 2.3. Assume that 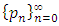is linearly convergent sequence to the limit p, then the sequence 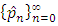that constructed by the acceleration (Aitken) formula

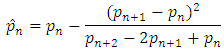, converges to p more rapidly than does the original sequence .

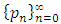Theorem 2.1. Let 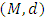be a complete metric space and 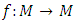be a contractive mapping on M, then f has a unique fixed point. Moreover, for any 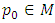the sequence of iterates 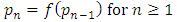converges to a fixed point of f.

Theorem 2.2. Let 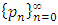be any sequence converging linearly to the limit p with 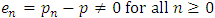. The sequence 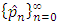converges to p faster than 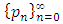in the sense .

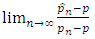3. The Application of Fixed Point Method (FPM) on LMVFIE2^nd

We consider the mixed Volterra-Fredholm integral equation (1.1) and define the operator T as follows

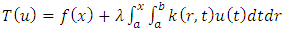(2)

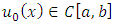Clearly, the solution of equation (1) is the fixed-point of operator T. By choosing the initial function , the following fixed-point iteration will be introduced

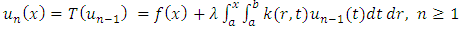(3)

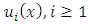several successive approximations will be determined by using equation (3.2), then the sequence of approximate solutions 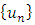will be produced which approaches the exact solution u as n approaches infinity. It is just the contractive property which is responsible for clustering the sequence 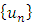in toward a limit point. Therefore the main concepts that are needed for fixed-point theorem are a complete metric space and a contractive mapping which would ensure the existence of a unique solution for the presented equation.

In the following, we show that under proper assumptions, T becomes a contractive mapping.

Theorem 3.1. Let 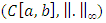be a complete metric space, and the functions k and f be continuous in their respective domain i.e. 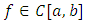and 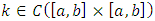, if additionally the following inequality

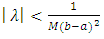(4)

satisfied, then the mapping T that defined in equation (2) becomes a contractive mapping.

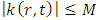Proof: First we indicate that the kernel is bounded that is for some positive real number M.

Let 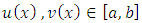, then

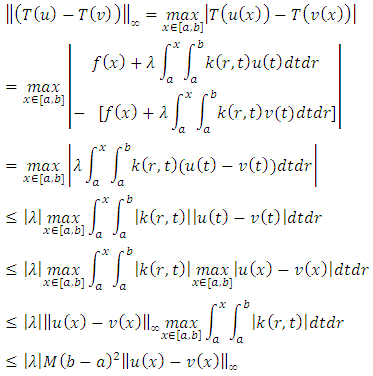Then with the assumption 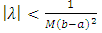we get that .

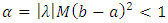Consequently, the mapping T of the linear Volterra-Fredholm integral equation becomes a contractive mapping.

4. The Existence and Uniqueness of Solution

To ensure the existence of a unique solution of the MVFIE2^nd, we have to show that T has a unique fixed-point and the sequence 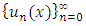generated by iteration (3) converges to this unique fixed-point.

Theorem 4.1. Let 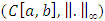be a complete metric space and T be a contractive mapping of MVFIE2^nd defined in (3)

then

i. T has a unique fixed-point

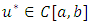ii. For any 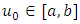the sequence of iterates 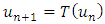converges to .

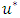Proof: i. By taking the limit of both sides of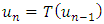

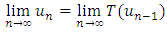Since T is contraction mapping, then it is continuous, so

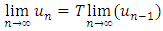Thus 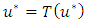. Hence T has a fixed-point.

Now, suppose that 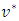is also a fixed-point of T, that is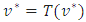

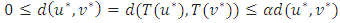Remembering that 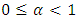, the above implies that

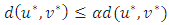This means that 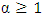, which is contradicts our assumption, therefore .

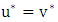ii. By the closer condition from part (i), we have:

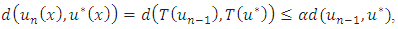also we have

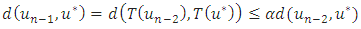that is we get

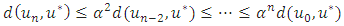Taking the limit of both sides produces

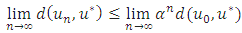Since 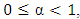, then 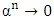, as 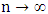, that is .

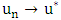5. The FPM Algorithm

To find an approximate solution of (LMVFIE2^nd) by FPM perform the following steps:

Step 1: select positive integers a, b, and n.

Step 2: put 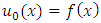as an initial approximation.

Step 3: calculate 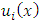in equation (3) for all .

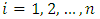Step 4: increment i and repeat the previous step until desired level of accuracy is reached.

Step 5: find .

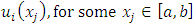Step 6: compute the absolute error of each root .

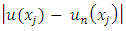6. Acceleration of Approximation (Aitken)

In this section, the possibility of improving the rate of convergence will be discussed for a slowly convergent sequence of iterates. The approach we adopt is due to Aitken. The idea is to use the terms of the sequence and their rate of change to predict the future behavior of the iteration. The proses are applicable to any linearly convergence.

Suppose that the sequence 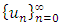is linearly convergent to the limit u. It follow that there exists a constant c, with 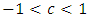, such that for sufficiently large value of n,

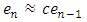(5)

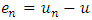where . It can be deduced that

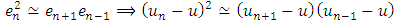we find that

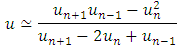(6)

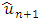this approximation will be denoted by and the errors 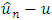by 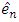. It will be found that the sequence 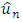is also convergent with the same limit u, but with a noticeably better approximation and faster rate of convergence as it stated in theorem (2.1).

7. Aitken on FPM for Solving MVFIE2^nd

In this section, the Aitken's method has been applied successfully on fixed-point method to find the solution of our integral equation, where the first three approximations are computed by fixed-point method and then substituted in equation (6) to get the procedure

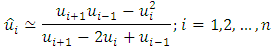(7)

where good estimations and sometimes exact solution will be found.

8. Numerical Examples

In this section, several examples will be solved to show the accuracy of our approach.

Example 1. Consider the following LMVFIE2^nd

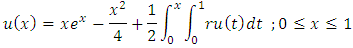where 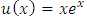is the exact solution.

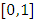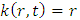Assume that f(x) is continuous on , and is continuous on the square 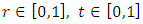, hence it is bounded there and a bound 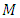is 1, that is

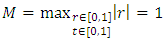, also we have

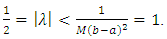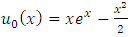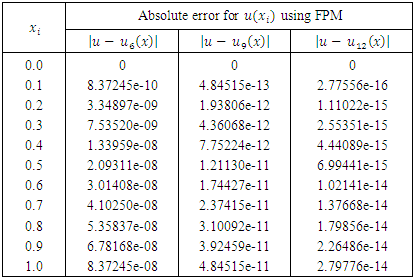
So according to the above theorem the problem has a unique solution and as described above, first we let , and then 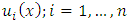will be determined. By choosing different values of (n), we will get the results that are listed in Table 1, while Figure 1 gives a comparison between the exact and the approximate solution using (F.P.) solution for different values of n.

Table 1. The results of Example 1 using FPM with n = 6, 9, 12 and Aitken method

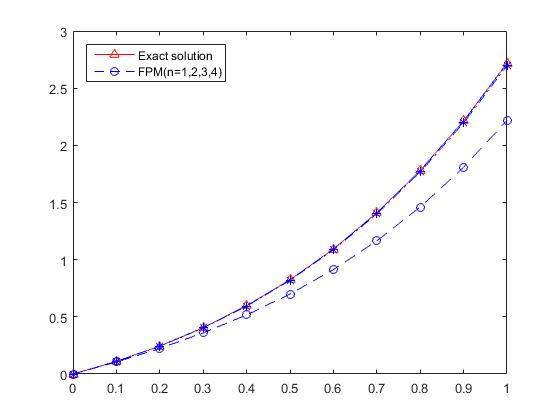Figure 1. Exact solutions and numerical results of example 1 using (F.P.) for n=1, 2, 3, and 4

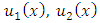Now to accelerate the convergence, the approximate solutions and 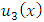will be found by FPM as follows:

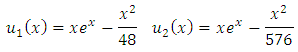and

and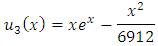 then substituted them in the Aitken procedure to get 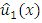which gives the exact solution with only one iteration.

Example 2. Consider the following LMVFIE2^nd

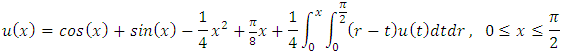where exact solution is .

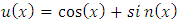First, it will be verified whether the described method can be used for solving this problem. Since and , therefore we only check the satisfying of inequality (10). In this example 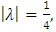and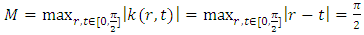

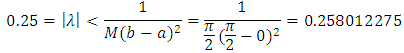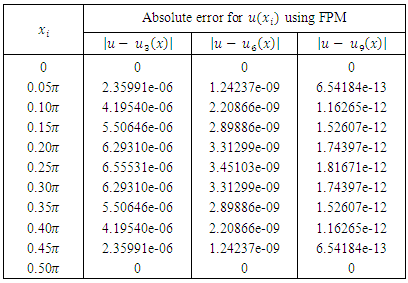
This means that FPM can be applied, Let 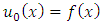, Applying the algorithm of the FPM with different values of n the following results that are listed in Table 2 are obtained, while Figure 2 gives a comparison between the exact and the approximate solution using (F.P.) solution for different values of n.

Table 2. The results of Example 2 using FPM with n = 3,6,9

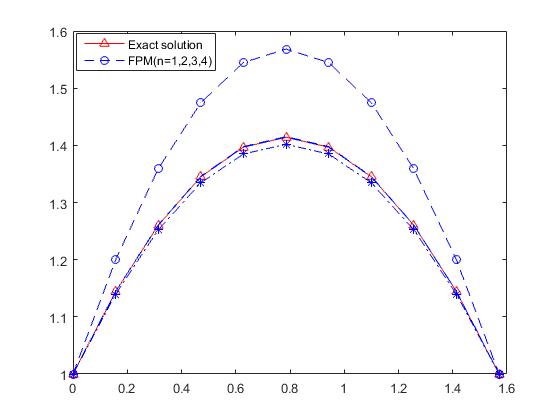Figure 2. Exact solutions and numerical results of example 2 using (F.P.) for n=1, 2, 3, and 4

9. Conclusions

In this paper, the existence and uniqueness of solution of linear mixed Volterra-Fredholm integral equation of the second kind (LSMVFIE2^nd) is verified and proved, the result is obtained by the help of some extensions of Banach's contraction principle in complete metric space. The fixed-point method introduced to solve the mentioned equation and then the solution is accelerated by Aitken formula. Two examples are presented for illustration and good approximate results are found. Moreover, the results of both of them (FPM & Aitken) are compared to each other and then with the exact solutions to demonstrate the implementation of the method. The given numerical examples and the outcomes in Tables (1-2) and Figures (1-2) are supported these claims.