-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2018; 8(5): 103-112
doi:10.5923/j.ajcam.20180805.03

Parameterized GGE Solving Linear Integer, Binary, or Mixed Programs (LIP, LBP, or LMP) (LIS-IV)
Paul T. R. Wang
WangPaul_Research.org, USA
Correspondence to: Paul T. R. Wang, WangPaul_Research.org, USA.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The author proposes an innovative approach that utilizes a single parameter as the gap between the objective values of a linear program and its associated linear integer, binary, or mixed programs (LIP, LBP, or/and LMP) with the concept of Generalized Gaussian Elimination (GGE) to resolve the feasibility of the associated linear Integer, binary, or mixed programs as to obtain the desired optimal solution if such a solution for LIP, LBP, or LMP does exist. Such an innovative LIP, LBP, or LMP solution technique does not require the traditional branch and bound (B&B) technique and it offers a computational complexity that is comparable to that of the GGE solution technique itself. Note that the computational complexity of the GGE approach is comparable to that of the original Gaussian Elimination (GE) for system of linear equalities. Sample LIP and LBP using this parameterized GGE to find their optimal solutions that match exactly to the answers obtained by the traditional B&B technique are provided to illustrate the correctness and simplicity of such a parameterized GGE (PGGE) approach for solving LIP, LBP, or LMP. Consequently, this PGGE is a new and effective solution technique much more powerful than the traditional B&B technique for LIP, LBP or LMP. Applying such a parameterized GGE solution technique to problems in the NP-Complete (NPC) group, one may be able to determine the overall computational complexity of the NP class and provide insight as to whether or not NP is also P? Furthermore, such a parameterized GGE technique is also applicable to resolve the feasibility of integer, binary, or mixed differential variation inequalities.
Keywords: Homogeneous Linear Systems, Feasible Intervals, Generalized Gaussian Elimination, LP, LBP, LIP, LMP, Differential Variation Inequalities, Computational Complexity, and NP-Completeness, Global, Recursive, and Greedy Optimization Algorithms
Cite this paper: Paul T. R. Wang, Parameterized GGE Solving Linear Integer, Binary, or Mixed Programs (LIP, LBP, or LMP) (LIS-IV), American Journal of Computational and Applied Mathematics , Vol. 8 No. 5, 2018, pp. 103-112. doi: 10.5923/j.ajcam.20180805.03.
Article Outline
1. Introduction
- Very large systems of linear inequalities with thousands or millions of variables and/or constraints are very tough to resolve. Typically, linear inequalities are solved with the famous Simplex method [1-4] the ellipsoid method [6], or the interior points method [7, 11]. For linear binary, integer, or mixed programs, classical Branch and Bond (B&B) technique [26] is used to locate the best solution if it does exist. Whether or not a linear system is solvable or whether or not a feasible linear system contains an integer, binary, or mixed solution is one of the most challenging questions known as NP-complete (NPC) for applications in operations research (OR) [10]. If problems in the NPC can be resolved as effectively as problems in P, one may be able to prove that NP is indeed also P. Recently, the author has shown that Gaussian Elimination for solving systems of linear equalities may be generalized to compute the feasible interval (unique, finite, unbounded, or null included) of each individual variable in terms of other variables with a computational complexity comparable to that of the original Gaussian Elimination method for systems of linear equalities [20].In this paper, the gap between the objective value of a linear integer, binary or mixed program and the objective value of the associated linear program excluding integer, binary, or mixed constraints as a relaxed or restricted linear program is used to control the feasible intervals of all variables such that optimal solution for LIP, BIP, or LMP is obtained. Since if both the LP and its associated LIP, LBP, or LMP are solvable with unique solutions, the gap between their associated objective values is also a fixed value that can be uniquely determined and verified using this parameterized GGE approach without the need of using the classical B&B procedure. Such a parameterized GGE is applied to sample LIP and LBP to obtain identical optimal solutions more effectively than they would be obtained through the traditional B&B approach. The difference between the traditional B&B and this PGGE searching approach for solutions of linear system is precisely the global, recursive, and greedy nature of PGGE versus the classical local nongreedy nature of B&B approach for solving linear systems.
2. Homogeneous Linear Systems Feasibility (HLSF) with New Notations [17-19]
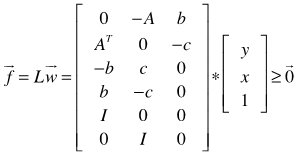
- Given any system of linear inequalities or equalities in vector and matrix form,
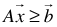 where
where 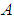 is an m by n matrix,
is an m by n matrix, 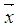 and
and 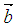 are m by 1 and n by 1 column vectors respectively. We define the homogeneous linear system feasibility (HLSF) for
are m by 1 and n by 1 column vectors respectively. We define the homogeneous linear system feasibility (HLSF) for 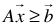 as follows
as follows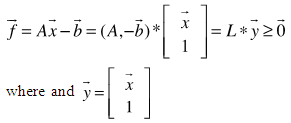 | (1) |
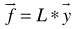 is referred to as the feasibility vector of the original linear system of inequalities
is referred to as the feasibility vector of the original linear system of inequalities 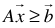 .Note that any system or subsystem of linear equalities
.Note that any system or subsystem of linear equalities 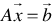 can always be converted into a system or subsystem of linear inequalities as
can always be converted into a system or subsystem of linear inequalities as 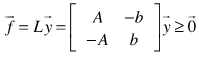 .The author adopted the following new notations to simplify the illustration of GGE:Let
.The author adopted the following new notations to simplify the illustration of GGE:Let 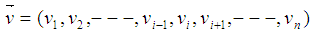 be an 1 by n row vector, and let
be an 1 by n row vector, and let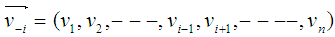 be the 1 by n-1 sub-vector of
be the 1 by n-1 sub-vector of 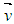 .With such a new notation, it is clear that for the dot product of two vectors
.With such a new notation, it is clear that for the dot product of two vectors 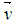 and
and 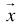 , we have,
, we have, 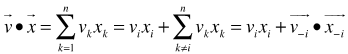 | (2) |
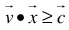 , we have
, we have 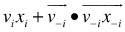 .Given the following homogenous linear inequality (HLI):
.Given the following homogenous linear inequality (HLI):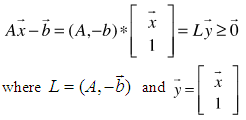 | (3) |
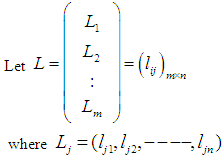 | (4) |
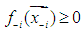 to highlight the nonexistence or absence of the variable,
to highlight the nonexistence or absence of the variable, 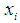 , from the function (either an equality or an inequality) for
, from the function (either an equality or an inequality) for 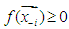 .
.2.1. A Literature Overview and Motivation
- Traditionally, linear inequalities are resolved as linear programs using either the Simplex methods (Dantzig, 1947), Crisis Cross algorithms (Fukuda & Terlaky, 1997), interior point method (Khachiyan, 1979), projective algorithms (Strang, 1987), path-following algorithms (Gondzio & Terlaky, 1996), and penalty or barrier functions (Nocedal and Wright, 1999). Most approaches centered on iterative searching for feasible points within the n dimensional polytope, i.e., the n-polytope, defined by the constraint linear inequalities. The author with his colleagues [18] proposed a new approach that recursively reduces the worst infeasibility, the sum of all infeasibility, and the number of constraints with the worst infeasibility based upon nonzero coefficients or a subset of the nonzero coefficients that defines the given system of linear inequalities [18]. Such an approach is capable of finding the exact solution if such a feasible solution is unique, a feasible solution if there is more than one solution. For a linear system that does not have a feasible solution, this approach is capable of minimizing the sum of all infeasibilitieies or the worst infeasibility, and pinpointing to the relevant coefficients to reveal true conflicts of the linear system [18].Over a five-year period from 2009 to 2014, three new techniques in dealing with linear systems with both equalities and inequalities were proposed by the author and his colleagues. The first technique (LIS-I) that examines the atomic components of system of linear inequalities is a set of algorithms that recursively reduce the sum of all infeasibilities, maximum infeasibility, and the number of constraints with the maximum infeasibility [17, 18]. Replacing variable substitution by variable transition, Gaussian Elimination for system of linear equalities does offer a generalized Gaussian Elimination (GGE) method that is capable of computing the feasible interval of an individual variable is done by LIS-II [20]. A third technique, LS-III, utilizes both projective and orthogonal geometry of unit vectors over the surface an n-dimensional hyperspace such as the unit-shell and the concepts of recursively finding equal distanced points to selected set of points on the unit shell with increasing rank to locate a solution if such a solution does exist [19]. In this paper, for every solvable linear program with its computed optimal value,
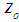 , a single parameter,
, a single parameter, 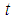 , is used to relax the objective value,
, is used to relax the objective value, 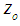 , such that the feasible intervals of all the variables that contain either the desired integer or binary solution and their associated objective value are uniquely determined.Such a single parameter driven GGE does not require B&B testing. It also preserves the computational complexity of both GE and GGE for any liner system with a finite number of variables or constraints. We provide sample LIP and LBP solved by this innovative technique as a parameterized GGE (PGGE) solution technique for LIP and LBP. Note that the PGGE approach may be applied recursively to LBP, LIP, or LMP in order to gradually increase the total number of variables as real, binary, integer, or desired mixed type. With the added variable as the gap of last best solution to selected neighboring feasible solutions, the PGGE is greedy in nature and will terminate with last best solution or no solution if the current feasible solution does not have a better neighboring desired binary, integer, or mixed type as
, such that the feasible intervals of all the variables that contain either the desired integer or binary solution and their associated objective value are uniquely determined.Such a single parameter driven GGE does not require B&B testing. It also preserves the computational complexity of both GE and GGE for any liner system with a finite number of variables or constraints. We provide sample LIP and LBP solved by this innovative technique as a parameterized GGE (PGGE) solution technique for LIP and LBP. Note that the PGGE approach may be applied recursively to LBP, LIP, or LMP in order to gradually increase the total number of variables as real, binary, integer, or desired mixed type. With the added variable as the gap of last best solution to selected neighboring feasible solutions, the PGGE is greedy in nature and will terminate with last best solution or no solution if the current feasible solution does not have a better neighboring desired binary, integer, or mixed type as 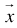 . The power of PGGE approach is due to the fact that the feasible interval (unique, undounded, or null) of a given variable,
. The power of PGGE approach is due to the fact that the feasible interval (unique, undounded, or null) of a given variable, 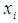 , can be uniquely and recursively computed as both lower bounds and upper bounds of the selected variable in terms of changes in all other vairables. Hence, the impact of any change of a single variable or simulatenaously changes of all variables to the feasible interval of a specific variable or variables of choice can be determined and computed to resolve inequalities feasibility issues. More specifically, the reason this can be done is that the feasible interval of a specific variable of a given linear system (LP, LBP, LIP, or LMP) may be computed from its maximum lower bound (mlb) and least upper bound (lub) which can be expressed as linear functions of other variables by column normalization corresponding to the variable of choice from its homogeneous linear form. The required variable type for real, binary or integer are enforced with rows added for both lower and upper bounds within the homogeneous linear form. Futhermore, equalities can always be treated as two opposite linear inequalities to account for difference in variable types and combined equalities with inequalities as demonstrated in this paper. Note that a linear system with equalities and inequalities combined has a solution only if the feasible intervals for all its variables are not null, namely,
, can be uniquely and recursively computed as both lower bounds and upper bounds of the selected variable in terms of changes in all other vairables. Hence, the impact of any change of a single variable or simulatenaously changes of all variables to the feasible interval of a specific variable or variables of choice can be determined and computed to resolve inequalities feasibility issues. More specifically, the reason this can be done is that the feasible interval of a specific variable of a given linear system (LP, LBP, LIP, or LMP) may be computed from its maximum lower bound (mlb) and least upper bound (lub) which can be expressed as linear functions of other variables by column normalization corresponding to the variable of choice from its homogeneous linear form. The required variable type for real, binary or integer are enforced with rows added for both lower and upper bounds within the homogeneous linear form. Futhermore, equalities can always be treated as two opposite linear inequalities to account for difference in variable types and combined equalities with inequalities as demonstrated in this paper. Note that a linear system with equalities and inequalities combined has a solution only if the feasible intervals for all its variables are not null, namely, 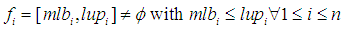 where n is the number of variables.
where n is the number of variables.3. Parameterized GGE for System of Linear Inequalities
- Given a solvable Linear Program (LP) and its associated Linear Integer Program (LIP), Linear Binary Program (LBP), or Linear Mixed Program (LMP) as:LP:
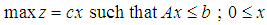 with the optimal value
with the optimal value 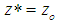 LIP:
LIP: 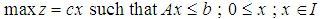 while
while 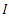 is the set of all integersLBP:
is the set of all integersLBP: 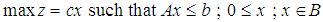 while
while 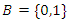 LMP:
LMP: 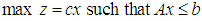
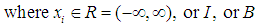 It is obvious that a solvable LIP, LBP, or LMP, its source LP, i.e., by removing some or all its integer or binary constraint or constraints to its variables must also be solvable; while the converse statement may not be true. A solvable LP does not imply its associated LIP, LBP, or LMP with added integer or binary constraints will also be solvable.Given a solvable source LP with its optimal value,
It is obvious that a solvable LIP, LBP, or LMP, its source LP, i.e., by removing some or all its integer or binary constraint or constraints to its variables must also be solvable; while the converse statement may not be true. A solvable LP does not imply its associated LIP, LBP, or LMP with added integer or binary constraints will also be solvable.Given a solvable source LP with its optimal value, 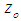 , computed by either the GGE (LIS-II) [20], Unit-Shell (LIS-III) [19], LIS-I [18], or other approaches such as the Simplex, ellipsoid, or interior points methods) [1 to 8], the following steps are required to implement the proposed parameterized GGE for LIP or LBP.Step 1: Convert the source LP to Homogeneous Linear Feasibility Form (HLF),
, computed by either the GGE (LIS-II) [20], Unit-Shell (LIS-III) [19], LIS-I [18], or other approaches such as the Simplex, ellipsoid, or interior points methods) [1 to 8], the following steps are required to implement the proposed parameterized GGE for LIP or LBP.Step 1: Convert the source LP to Homogeneous Linear Feasibility Form (HLF), 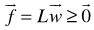 as described in the GGE paper [20]; solve the original LP by GGE to obtain its unique solution as
as described in the GGE paper [20]; solve the original LP by GGE to obtain its unique solution as 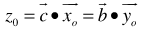 if (5) is solvable; namely the feasible interval for each
if (5) is solvable; namely the feasible interval for each  is unique for all
is unique for all  .
. | (5) |
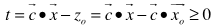 be the gap between the optimal objective value of an LP and the objective value of the associated LBP, LIP, or LMP. For LBP, LIP, or LMP to be solvable, we only have to add the following three constraints as inequalities:
be the gap between the optimal objective value of an LP and the objective value of the associated LBP, LIP, or LMP. For LBP, LIP, or LMP to be solvable, we only have to add the following three constraints as inequalities: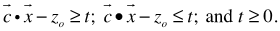 Consequently, for LIP, LBP, or LMP defined as
Consequently, for LIP, LBP, or LMP defined as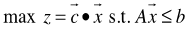 with
with 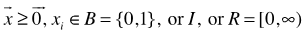 The feasible intervals for
The feasible intervals for 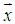 computed must contain the desirable integer, binary, or real values. Hence, we define the following linear inequalities for LIP or LBP respectively as:
computed must contain the desirable integer, binary, or real values. Hence, we define the following linear inequalities for LIP or LBP respectively as: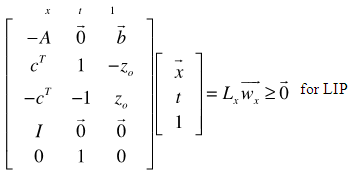 | (6) |
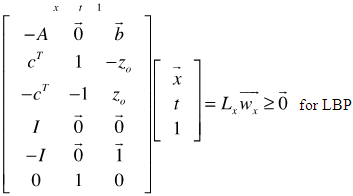 | (7) |

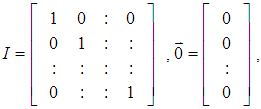 and
and 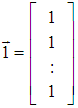 .Step 2: Normalize each column of
.Step 2: Normalize each column of 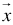 in (6 or 7) such that the coefficients of that column
in (6 or 7) such that the coefficients of that column  are either 1, 0, or -1 (by dividing row
are either 1, 0, or -1 (by dividing row  with
with 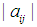 for column
for column 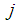 ). Equivalently. We have:
). Equivalently. We have: 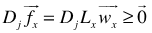 where
where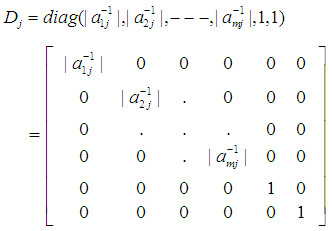 | (8) |
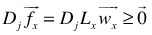 uniquely defines the feasible interval
uniquely defines the feasible interval 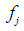 of
of 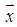 as linear functions of the parameter,
as linear functions of the parameter, 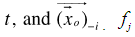 can be computed (uniquely as null, unbounded, finite, or single value) whether or not the optimal LIP, LBP, or LMP is solvable with an optimal objective value
can be computed (uniquely as null, unbounded, finite, or single value) whether or not the optimal LIP, LBP, or LMP is solvable with an optimal objective value 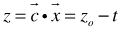 If there is a finite and positive value of
If there is a finite and positive value of 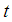 (the minimum value
(the minimum value 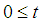 such that all the feasible intervals of
such that all the feasible intervals of 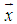 contain at least the desired type of integer, binary, or real number.Step 3: Compute the feasible interval
contain at least the desired type of integer, binary, or real number.Step 3: Compute the feasible interval 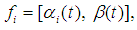 for individual variable,
for individual variable, 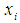 of
of 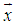 as a linear function in
as a linear function in 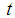 and
and 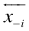 from Step 2 Consequently, LIP or LBP (6 or 7) is solvable only if there is minimum
from Step 2 Consequently, LIP or LBP (6 or 7) is solvable only if there is minimum 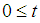 such that
such that 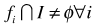 (or
(or 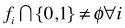 ). For mixed LMP, slightly modified (6 or 7) is required to exclude or include the desired nonbinary or noninteger variables.Step 4: From the last
). For mixed LMP, slightly modified (6 or 7) is required to exclude or include the desired nonbinary or noninteger variables.Step 4: From the last 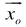 and
and 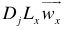 the feasible interval for
the feasible interval for 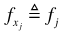 for
for 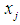 can be computed. Each feasible interval
can be computed. Each feasible interval 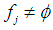 has two end points: maximum lower bound (mlb) and least upper bound (lub) with mlb
has two end points: maximum lower bound (mlb) and least upper bound (lub) with mlb 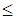 lub. By substituting
lub. By substituting 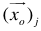 with the end points of
with the end points of 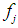 we have at most 2n neighboring potential feasible solutions for (6 or 7) or if
we have at most 2n neighboring potential feasible solutions for (6 or 7) or if 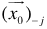 and the selected end point as
and the selected end point as 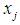 remains feasible in (6 or 7). Note that
remains feasible in (6 or 7). Note that 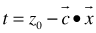 can be computed for each of the 2n cases. Compute new feasible interval
can be computed for each of the 2n cases. Compute new feasible interval 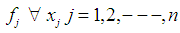 .Step 5: Among the 2n cases, select only cases with
.Step 5: Among the 2n cases, select only cases with 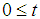 and
and 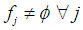 and recompute
and recompute 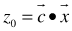 and
and 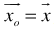 .Repeat Steps 3 to 5 recursively until no more feasible
.Repeat Steps 3 to 5 recursively until no more feasible 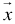 exists; i.e., termination occurs at Step 3.
exists; i.e., termination occurs at Step 3.4. Highlight of PGGE for LIP, LBP, or LMP
- In summary, the PGGE for LIP, LBP, or LMP is a natural extension of GGE to resolve the feasibility issues of mixed or pure LIP, LBP, LMP, or LP. It is recursively and agreesively applied to the current best solution as a new linear optimization technique that only solves LP with GGE or other LP solution techniques once. The search for LBP, LIP, or LMP solution is done by recomputing all feasible intervals based upon column nomalization, and computed gap between last optimal solution and the neighboring feasible solutions globally. No branch and bound search and repeatedly solving new LPs on the binary search tree is required to locate the optimal and desired solution. Consequently, PGGE is suitable for very large linear systems with millions of variables and may be speeded up further with an advanced paralleling computing facility and setup that current B&B techniques may offer.
5. Examples
- To illustrate the applicability of parameterized GGE for LIP or LBP, Consider the following LIP
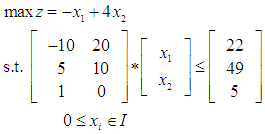 | (9) |
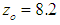 with
with 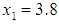 and
and 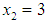 .
.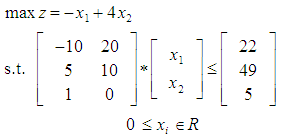 | (10) |
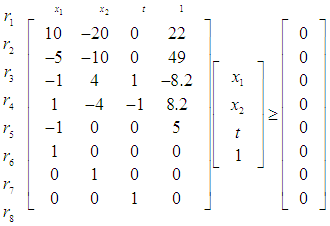 | (11) |
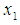 as:
as: | (12) |
 | (13) |
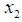 as:
as: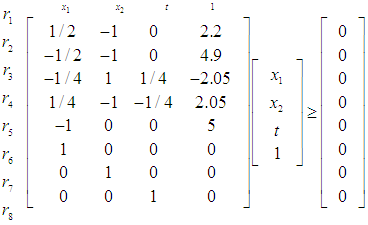 | (14) |
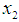
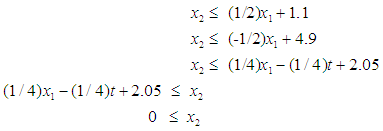 | (15) |
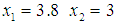 , and
, and 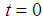 . There are 4 neighboring mixed real and integral cases where there are more or equal number of integers
. There are 4 neighboring mixed real and integral cases where there are more or equal number of integers 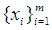 as
as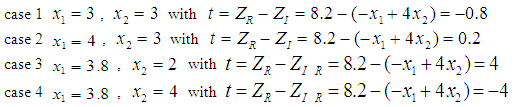 Note that both case 1 and case 4, we have
Note that both case 1 and case 4, we have 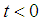 , case 2 has the smallest
, case 2 has the smallest 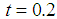 , from (15) with
, from (15) with 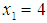 and
and 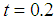 , and the feasible interval for
, and the feasible interval for 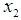 is
is 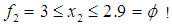 Hence, case 3 is the best choice with
Hence, case 3 is the best choice with 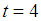 , and the feasible interval for
, and the feasible interval for 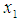 from (13) is
from (13) is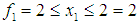 . Also
. Also 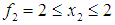 from (15). Hence, the optimal solution for LIP (9) is
from (15). Hence, the optimal solution for LIP (9) is 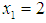 ,
, 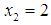 with
with 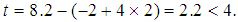 A second example for solving LBP with the parameterized GGE is demonstrated as following:
A second example for solving LBP with the parameterized GGE is demonstrated as following: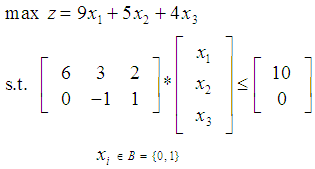 | (16) |
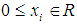 has an optimal solution as
has an optimal solution as 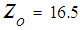 with
with 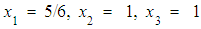 .Convert the LBP (16) with
.Convert the LBP (16) with 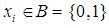 for all
for all 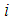 to Homogeneous Linear Feasibility Form (HLF), as described in section 3. as
to Homogeneous Linear Feasibility Form (HLF), as described in section 3. as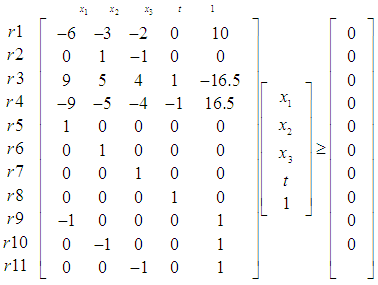 | (17) |
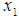 , we have
, we have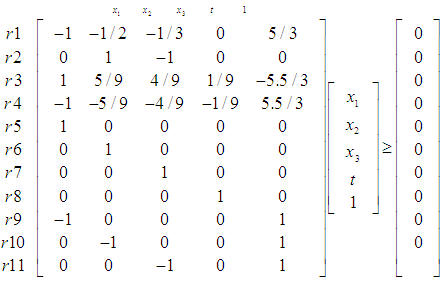 | (18) |
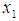 as:
as: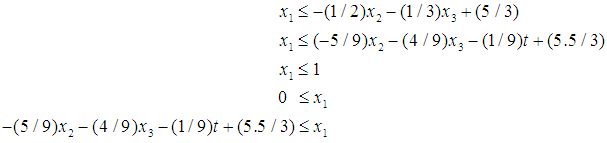 | (19) |
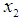 form (17), we have
form (17), we have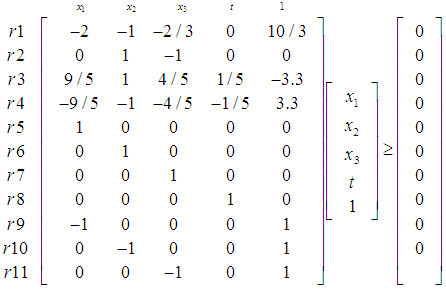 | (20) |
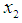 as:
as: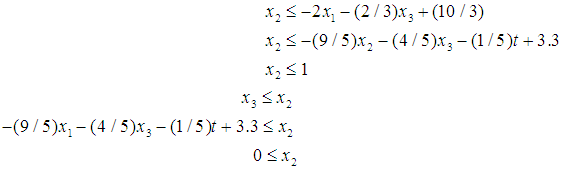 | (21) |
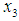 form (17), we have
form (17), we have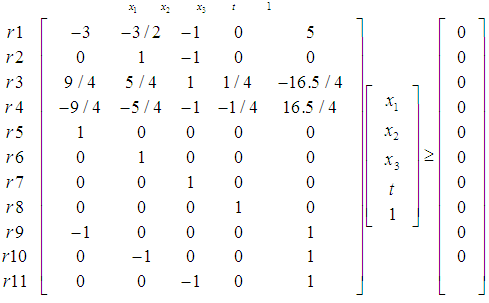 | (22) |
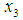 as:
as: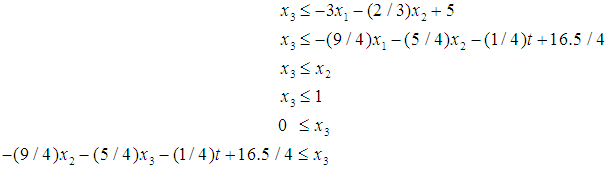 | (23) |
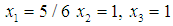 , and
, and 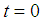 , there are 4 neighboring mixed real and boolean cases with more or equal number of boolean
, there are 4 neighboring mixed real and boolean cases with more or equal number of boolean 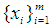 as:
as: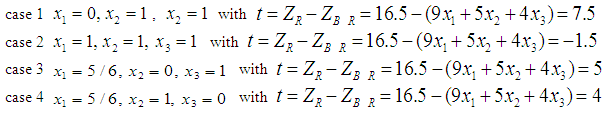 Inequalities (19), (21), and (23) provide both lower bounds and upper bounds for each variable
Inequalities (19), (21), and (23) provide both lower bounds and upper bounds for each variable 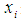 for
for 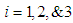 . The feasible interval for each variable
. The feasible interval for each variable 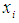 is
is 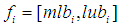 where
where 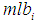 is the maximum lower bounds and
is the maximum lower bounds and 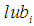 is the least upper bounds for variable
is the least upper bounds for variable 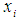 . Hence, we have:case 1 we have
. Hence, we have:case 1 we have 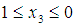 ; hence the feasible interval for
; hence the feasible interval for 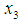 is
is 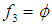 .case 2 we have
.case 2 we have 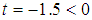 case 3 we have
case 3 we have 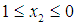 ; henace the feasible interval for
; henace the feasible interval for 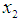 is
is 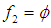 .case 4 we have
.case 4 we have 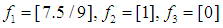 We can apply the same argument with the best mixed linear solutions, LMP, for (16) as
We can apply the same argument with the best mixed linear solutions, LMP, for (16) as 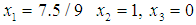 , and
, and 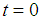 , there are only two neighboring mixed real and boolean cases with more or equal number of binary
, there are only two neighboring mixed real and boolean cases with more or equal number of binary 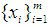 as:
as: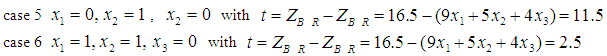 Note that for the neighboring binary solution with
Note that for the neighboring binary solution with 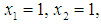 and
and 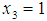 we have
we have 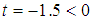 as shown in case 2. Hence, we have the LBP solution as
as shown in case 2. Hence, we have the LBP solution as 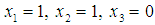 with the minimum
with the minimum 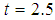 for (16).
for (16).6. Conclusions and Future Work
- In conclusion, the author proposes a unique parameter to recursively reduce the gap of solutions between a linear program and its associated as a relaxed or restricted integer, binary, and/or mixed linear program based upon the generalization of the traditional Gaussian elimination (GE) as a Parameterized and Generalized Gaussian Elimination (namely, PGGE) for solving a system of linear inequalities by computing the feasible intervals of all variables in order to resolve the feasibility of all linear systems with both equalities and/or inequalities included. This PGGE technique may be utilized to handle all linear systems for binary, integer, or mixed programs with both equalities, and inequalities included. Note that the Generalized Gaussian Elimination (GGE) for linear systems is applicable to a wide range of engineering and scientific applications and is related closely to the NPC mystery of the operations research and the solvability of differential variation inequalities (DVI). Furthermore, it can be shown that GE is indeed a special case of GGE and that both GGE and GE do share the same worst case computational complexity of
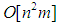 where n is the number of variables and m is the number of constraints. This is accomplished by replacing the variable substitution of the Gaussian elimination method by variable transition such that a specific variable may be safely and recursively eliminated without losing its binding inequalities and preserving both the maximum lower bounds (i.e., the greatest lower bound) (MLB) and the least upper bound (LUB). With the PGGE approach, individual variable’s lower bounds and upper bounds can be computed as linear functions of other variables and its feasible interval determined for any changes and its impact on the gap between optimal LP, LBP, LIP, and LMP recursively computed to locate optimal solution or solutions when such solution or solutions exist. By adding a single paramater to recursively control the gap between the last optimal solutions of a linear real, integer, binary, or mixed program and its neighboring linear programs, it is shown that any linear system with mixed linear equalities and inequalities may be converted into its standard homogeneous form such that the proposed GGE algorithm and PGGE algorithms may be applied to obtain the new feasible intervals of all variables uniquely determnined by this control paramater and other variables recursively. From the feasible intervals of all the variables of a given linear system, one may determine whether or not it contains binary, integers, or mixed solutions. The correctness and validity of GGE is illustrated by solving sample linear programs with unique solution, unbounded solution, and no solution [20]. In this paper, the author utilizes a single parameter,
where n is the number of variables and m is the number of constraints. This is accomplished by replacing the variable substitution of the Gaussian elimination method by variable transition such that a specific variable may be safely and recursively eliminated without losing its binding inequalities and preserving both the maximum lower bounds (i.e., the greatest lower bound) (MLB) and the least upper bound (LUB). With the PGGE approach, individual variable’s lower bounds and upper bounds can be computed as linear functions of other variables and its feasible interval determined for any changes and its impact on the gap between optimal LP, LBP, LIP, and LMP recursively computed to locate optimal solution or solutions when such solution or solutions exist. By adding a single paramater to recursively control the gap between the last optimal solutions of a linear real, integer, binary, or mixed program and its neighboring linear programs, it is shown that any linear system with mixed linear equalities and inequalities may be converted into its standard homogeneous form such that the proposed GGE algorithm and PGGE algorithms may be applied to obtain the new feasible intervals of all variables uniquely determnined by this control paramater and other variables recursively. From the feasible intervals of all the variables of a given linear system, one may determine whether or not it contains binary, integers, or mixed solutions. The correctness and validity of GGE is illustrated by solving sample linear programs with unique solution, unbounded solution, and no solution [20]. In this paper, the author utilizes a single parameter, 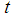 , to recursively compute feasible intervals for all variables and locate the desired optimal real, binary, integer, or mixed solutions for a given linear system.Future work of this research includes the implementation of PGGE as java code and Excel VB functions for very large systems of linear inequalities or mixed of linear equalities and inequalities with millions of variables and/or constraints. The proposed PGGE techniques may be applied to most members of the NPC class of problems in Operations Research applicarions. Funding from NSF or private foundations will be pursued to speed up the development of Java or VB functional codes for solving eigenvector systems, computing orthogonal basis, and DVI applications. PGGE may also be applied to problems in operations research to reveal the availability of integer, binary, or mixed solutions encountered in the NPC mystery as open issue on whether or not NP is indeed also P ?! [27].
, to recursively compute feasible intervals for all variables and locate the desired optimal real, binary, integer, or mixed solutions for a given linear system.Future work of this research includes the implementation of PGGE as java code and Excel VB functions for very large systems of linear inequalities or mixed of linear equalities and inequalities with millions of variables and/or constraints. The proposed PGGE techniques may be applied to most members of the NPC class of problems in Operations Research applicarions. Funding from NSF or private foundations will be pursued to speed up the development of Java or VB functional codes for solving eigenvector systems, computing orthogonal basis, and DVI applications. PGGE may also be applied to problems in operations research to reveal the availability of integer, binary, or mixed solutions encountered in the NPC mystery as open issue on whether or not NP is indeed also P ?! [27].ACKNOWLEDGEMENTS
- Generalization of the classical Gaussian elimination for linear systems to cover inequalities is the result of years of inquiry and discussion with Dr. Leone C. Monticone and Dr. William P. Niedringhaus, colleagues of the author at the MITRE Corporation where the author served as an aviation engineer. The author also was benefited professionally and intellectually from his colleagues, Dr. Leonard Wojcik and Mr. Matt McMahon during many years at the MITRE Corporation working on MITRE sponsored research (MSR) projects related to solving very large linear systems. The PGGE approach is entirely developed by the author after his retirement from the MITRE Corporation in 2013. Review and editorial advice from SAP and AJCAM are also essential to the improved quality and readability of this paper.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML