-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2018; 8(5): 93-102
doi:10.5923/j.ajcam.20180805.02

h, k, NA: Evaluating the Relative Uncertainty of Measurement
Boris Menin
Mechanical & Refrigeration Consultation Expert, Beer-Sheba, Israel
Correspondence to: Boris Menin, Mechanical & Refrigeration Consultation Expert, Beer-Sheba, Israel.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

For verification of the measurement accuracy of fundamental physical constants, the CODATA unique technique is used. This procedure is a complex process based on a careful discussion of the input data, and the justification and construction of tables of values sufficient for the direct use of the relative uncertainty are conducted using modern advanced statistical methods and powerful computers. However, at every stage of data processing, researchers must rely on common sense, that is, an expert conclusion. In this article, the author proposes a theoretical and informational grounded justification for calculating the relative uncertainty by using the comparative uncertainty. A detailed description of the data and the processing procedures do not require considerable time. Examples of measurements results of three fundamental constants are analysed, applying information-oriented approach. Comparison of the achieved relative and comparative uncertainties is introduced and discussed.
Keywords: Avogadro number, Boltzmann constant, Planck constant, Information theory, Comparative and relative uncertainties
Cite this paper: Boris Menin, h, k, NA: Evaluating the Relative Uncertainty of Measurement, American Journal of Computational and Applied Mathematics , Vol. 8 No. 5, 2018, pp. 93-102. doi: 10.5923/j.ajcam.20180805.02.
Article Outline
1. Introduction
- It is expected that in 2018 that the International System of Units (SI) will be redefined on the basis of certain values of some fundamental constants [1]. This is a dramatic change, one consequence of which is that there will no longer be a clear distinction between the base quantities and derived quantities [2].Recommended CODATA values and units for constants [3] are based on the conventions of the current SI, and any modifications to these conventions will have implications for the units. One consequence of this difference is that mathematics does not provide information on how to include units in the analysis of physical phenomena. One of the goals of the SI is to provide a systematic structure for including units in equations describing physical phenomena.The desire to reduce the value of uncertainty in the measurement of fundamental physical constants is due to several reasons. First, the achievement of an accurate quantitative description of the physical universe depends on the numerical values of the constants that appear in theories. Secondly, the general consistency and validity of the basic theories of physics can be proved by carefully studying the numerical values of these constants, determined from different experiments in different fields of physics.One needs to note the main feature of the CODATA technique in determining the relative uncertainty of one fundamental physical constant or the other. For using CODATA technique based on solid principles of probability and statistics, tables of values that allow direct use of relative uncertainty are constructed, using modern advanced statistical methods and powerful computers. This, in turn, allows for checking the consistency of the input data and the output set of values. However, at every stage of data processing, one needs to use her or his intuition, knowledge and experience (one's personal philosophical leanings [4]). In addition, it should be that the concept of relative uncertainty was used when considering the accuracy of the achieved results (absolute value and absolute uncertainty of the separate quantities and criteria) during the measurement process in different applications. However, this method for identifying the measurement accuracy does not indicate the direction of deviation from the true value of the main quantity. In addition, it involves an element of subjective judgment [5].Let us start with the disclaimer: the author does not promote the CODATA method and does not blame him. The author draws attention to the fact that the introduction of a statistical-expert method for estimating the accuracy of measurement of a fundamental physical constant assumes, by default, the existence of such nonprofessional criteria that are not accepted at scientific conferences, are not resolved for publication in scientific journals and are simply not mentioned in personal conversations: the desire to promote their own project, the desire to obtain additional investment to continue experiments, and to achieve international recognition of the achieved results. Apparently, this situation suits most researchers. The aim of this paper is an introduction of information-oriented approach [6] for analyzing measurement of fundamental physical constants along with a relative uncertainty, by a comparative uncertainty and to compare results. It is explained by the fact that in the framework of the information approach, a theoretical and informational grounding and justification is carried out for calculating the relative uncertainty.
2. Information Approach
- During modeling process, scientists use quantities inherent in the SI. SI is generated by the collective imagination. SI is an instrument, which is characterized by the presence of the equiprobable accounting of any quantity by a conscious observer that develops the model due his knowledge, intuition, and experience. Each quantity allows the researcher to obtain a certain amount of information about the studied object. The total number of quantities can be calculated, and this corresponds to the maximum amount of information contained in the SI. In addition, every experimenter selects a particular class of phenomena (CoP) to study the measurement process of the fundamental physical constant. CoP is a set of physical phenomena and processes described by a finite number of base and derived quantities that characterize certain features of the object [7]. For example, in mechanics, SI uses the basis {the length L, weight M, time Т}, that is, CoPSI
 LMТ. Surprisingly, one can calculate the total number of dimensional and dimensionless quantities inherent in SI. By that, to calculate the first-born, absolute uncertainty in determining the dimensionless researched main quantity, "embedded" in a physical-mathematical model and caused only by the limited number of chosen quantities. It can be organized following the below mentioned steps:(1) There are ξ = 7 base quantities: L is the length, M is the mass, Т is time, I is the electric current, Θ is the thermodynamic temperature, J is the luminous intensity, F is the amount of substances [8];(2) The dimension of any derived quantity q can only be expressed as a unique combination of dimensions of the main base quantities to different powers:
LMТ. Surprisingly, one can calculate the total number of dimensional and dimensionless quantities inherent in SI. By that, to calculate the first-born, absolute uncertainty in determining the dimensionless researched main quantity, "embedded" in a physical-mathematical model and caused only by the limited number of chosen quantities. It can be organized following the below mentioned steps:(1) There are ξ = 7 base quantities: L is the length, M is the mass, Т is time, I is the electric current, Θ is the thermodynamic temperature, J is the luminous intensity, F is the amount of substances [8];(2) The dimension of any derived quantity q can only be expressed as a unique combination of dimensions of the main base quantities to different powers: 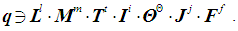 | (1) |
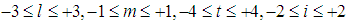 | (2) |
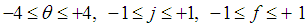 | (3) |
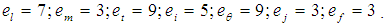 | (4) |
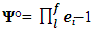
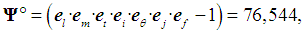 | (5) |
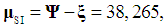 | (6) |
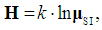 | (7) |
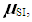 equally probable accounted quantities,
equally probable accounted quantities, 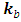 is the Boltzmann's constant. (8) When a researcher chooses the influencing factors (the conscious limitation of the number of quantities that describe an object, in comparison with the total number µSI), entropy of the mathematical model changes a priori. Then one can write
is the Boltzmann's constant. (8) When a researcher chooses the influencing factors (the conscious limitation of the number of quantities that describe an object, in comparison with the total number µSI), entropy of the mathematical model changes a priori. Then one can write 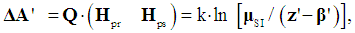 | (8) |
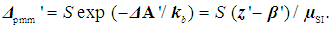 | (9) |
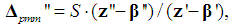 | (10) |
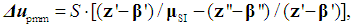 | (11) |
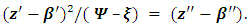 | (12) |
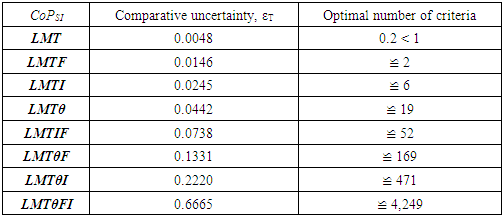
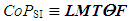 is usually used. In this case the minimum comparative uncertainty (εmin)LMTθF can be calculated by the following way:
is usually used. In this case the minimum comparative uncertainty (εmin)LMTθF can be calculated by the following way: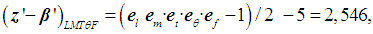 | (13) |
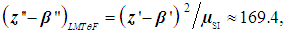 | (14) |
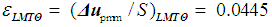 | (15) |
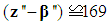 | (16) |
|
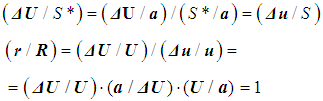 | (17) |
3. Formulation of Procedure
- If the range of observation S is not defined, the information obtained during the observation/measurement cannot be determined, and the entropic price becomes infinitely large [10]. In the framework of the information-oriented approach, it seems that the theoretical limit of the absolute and relative uncertainties depends on the empirical value, that is, possible interval of placing (the observed range of variations) S of the measured physical constant. In other words, the results will be completely different if a larger interval of changes is considered in the measured fundamental physical constant. It is right, however, if S is not declared, the information obtained in the measurement cannot be determined. Any specific measurement requires a certain (finite) a priori information about the components of the measurement and interval of observation of the measured quantity. These requirements are so universal that it acts as a postulate of metrology [11]. This, the observed range of variations, depends on the knowledge of the developer before undertaking the study. "If nothing is known about the system studied, then S is determined by the limits of the measuring devices used" [10]. That is why, taking into account Brillouin’s suggestions, there are two options of applying the conformity principle to analyze the measurement data of the fundamental physical constants. First, this principle dictates, factually, analyzing the data of the magnitude of the achievable relative uncertainty at the moment taking into account the latest results of measurements. The extended range of changes in the quantity under study S indicates an imperfection of the measuring devices, which leads to a large value of the relative uncertainty. The development of measuring technology, the increase in the accuracy of measuring instruments, and the improvement in the existing and newly created measurement methods together lead to an increase in the knowledge of the object under study and, consequently, the magnitude of the achievable relative uncertainty decreases. However, this process is not infinite and is limited by the conformity principle. The reader should bear in mind that this conformity principle is not a shortcoming of the measurement equipment or engineering device, but of the way the human brains work. When predicting behavior of any physical process, physicists are, in fact, predicting the perceivable output of instrumentation. It is true that, according to the µ-hypothesis, observation is not a measurement, but a process that creates a unique physical world with respect to each particular observer. Thus, in this case, the range of observation (possible interval of placing) of the fundamental physical constant S is chosen as the difference between the maximum and minimum values of the physical constant measured by different scientific groups during a certain period of recent years. Only in the presence of the results of various experiments one can speak about the possible appearance of a measured value in a certain range. Thus, using the smallest attainable comparative uncertainty inherent in the selected class of phenomena during measuring the fundamental constant, it is possible to calculate the recommended minimum relative uncertainty that is compared with the relative uncertainty of each published study. In what follows, this method is denoted as IARU and includes the following steps:(1) From the published data of each experiment, the value z, relative uncertainty rz and standard uncertainty uz (possible interval of u placing) of the fundamental physical constant are chosen;(2) The experimental absolute uncertainty Δz is calculated by multiplying the fundamental physical constant value z and its relative uncertainty rz attained during the experiment, Δz = z · rz; (3) The maximum zmax and minimum zmin values of the measured physical constant are selected from the list of measured values zi of the fundamental physical constant mentioned in different studies; (4) As a possible interval for placing the observed fundamental constant Sz, the difference between the maximum and minimum values is calculated, Sz = zmax - zmin; (5) The selected comparative uncertainty εT (Table 1) inherent in the model describing the measurement of the fundamental constant is multiplied by the possible interval of placement of the observed fundamental constant Sz to obtain the absolute experimental uncertainty value ΔIARU in accordance with the IARU, ΔIARU = εT · Sz; (6) To calculate the relative uncertainty rIARU in accordance with the IARU, this absolute uncertainty ΔIARU is divided by the arithmetic mean of the selected maximum and minimum values, rIARU = ΔIARU / ((zmax + zmin)/2); (7) The relative uncertainty obtained rIARU is compared with the experimental relative uncertainties ri achieved in various studies;(8) According to IARU, a comparative experimental uncertainty of each study, εIARUi is calculated by dividing the experimental absolute uncertainty of each study Δz on the difference between the maximum and minimum values of the measured fundamental constant Sz, εIARUi = Δz / Sz. These calculated comparative uncertainties are also compared with the selected comparative uncertainty εT (Table 1). Second, S is determined by the limits of the measuring devices used [10]. This means that as the observation interval in which the expected true value of the measured fundamental physical constant is located, a standard uncertainty is selected when measuring the physical constant in each particular experiment. Compared with various fields of technology, experimental physics is better for the fact that in all the researches, the experimenters introduce the output data of the measurement with uncertainty bars. At the same time, it should be remembered that the standard uncertainty of a particular measurement is subjective, because the conscious observer probably did not take into account this or that uncertainty. The experimenters calculate the standard uncertainty, taking into account all possibilities, they noticed the measured uncertainties. Then, one calculates ratio between the absolute uncertainty reached in an experiment and standard uncertainty, acting as a possible interval for allocating a fundamental physical constant. So, in the framework of the information approach, the comparative uncertainties achieved in the studies are calculated, which in turn are compared with the theoretically achievable comparative uncertainty inherent in the chosen class of phenomena. Standard uncertainty can be calculated also for quantities that are not normally distributed. Transformation of different types of uncertainty sources into standard uncertainty is very important. In what follows, this method is denoted as IACU and includes the following steps.(1) From the published data of each experiment, the value z, relative uncertainty rz and standard uncertainty uz (possible interval of placing) of the fundamental physical constant are chosen;(2) The experimental absolute uncertainty Δz is calculated by multiplying the fundamental physical constant value z and its relative uncertainty rz attained during the experiment, Δz = z · rz;(3) The achieved experimental comparative uncertainty of each published research εIACUi is calculated by dividing the experimental absolute uncertainty Δz on the standard uncertainty uz, εIACUi = Δz / uz;(4) The experimental calculated comparative uncertainty εIACUi is compared with the selected comparative uncertainty εT (Table 1) inherent in the model, which describes the measurement of the fundamental constant. We will apply IARU and IACU in analyzing the data measurement of the three fundamental physical constants h, k, NA.
4. Applications
4.1. Planck Constant h
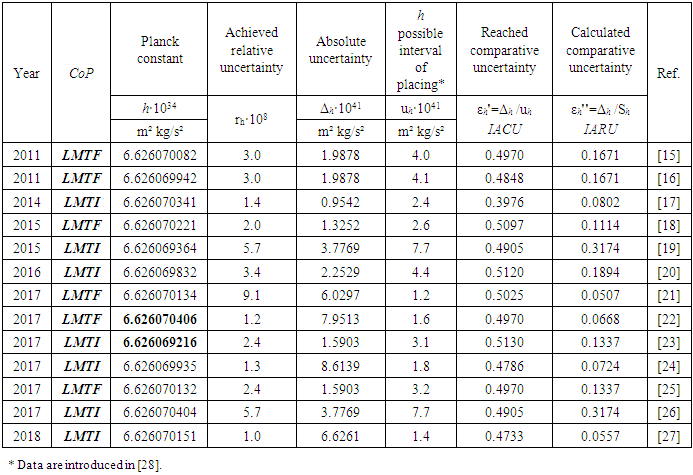
- Planck constant h is of great importance in modern physics. It is explained by the following reasons [12]: (a) It defines the quanta (minimum amount) for the energy of light and therefore also the energies of electrons in atoms. The existence of a smallest unit of light energy is one of the foundations of quantum mechanics.(b) It is a factor in the Uncertainty Principle, discovered by Werner Heisenberg in 1927;(c) Planck constant has enabled the construction of the transistors, integrated circuits, and chips that have revolutionized our lives.(d) For over a century, the weight of a kilogram has been determined by a physical object, but that could change in 2018 under a new proposal that would base it on Planck constant.Therefore, a huge amount of researches were dedicated to the Planck constant measurement [13]. The most summarized data published in scientific journals in recent years, about the magnitude of the standard uncertainty of the Planck constant and the Boltzmann constant measurements are presented in [14]. The measurements, made during 2011-2018, were analyzed for this study. The data are summarized in Table 2 [15-27]. It has been demonstrated that two methods have the capability of realizing the kilogram according to its future definition with relative standard uncertainties of a few parts in 108: the Kibble balance (CoPSI ≡ LMТI) and the x-ray crystal density (XRCD) method (CoPSI ≡ LMТF).
|
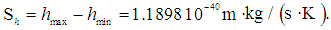 | (18) |
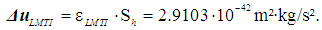 | (19) |
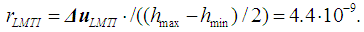 | (20) |
4.2. Boltzmann Constant k
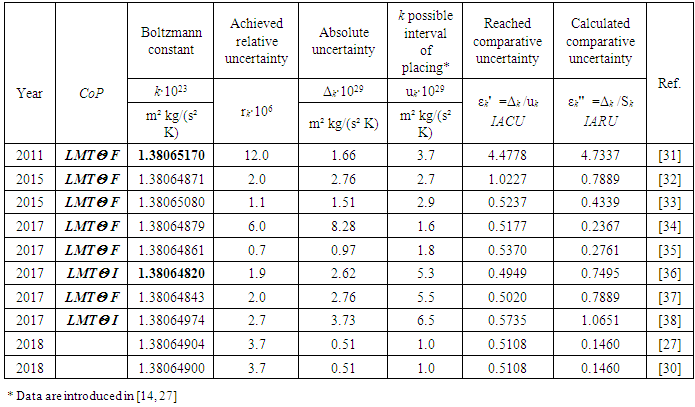
- The analysis of the Boltzmann constant k plays an increasingly important role in our physics today to ensure the correct contribution to the next CODATA value and to the new definition of the Kelvin. This task is more difficult and crucial when its true target value is not known. This is the case for any methodologies intended to look at the problem from a possible another view and which, may have different constraints and need special discussion. A detailed analysis of the measurements of Boltzmann constant made since 1973 is available in [27, 30]. The more recent of these measurements, made during 2011-2018 [27, 30-38], were analyzed for this study. The data are summarized in Table 3. The noted scientific articles, in most cases belong to CoPSI ≡ LMТF [31-35, 37], some to CoPSI ≡ LMТI [36, 38]. Although the authors of the research studies cited in these papers mentioned all the possible sources of uncertainty, the values of absolute and relative uncertainties can still differ by more than two times. And, a similar situation exists in the spread of the values of comparative uncertainty.
|
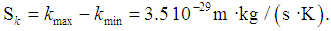 | (21) |
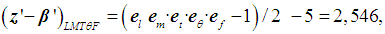 | (22) |
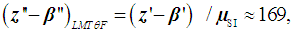 | (23) |
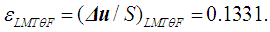 | (24) |
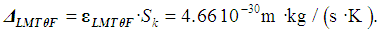 | (25) |
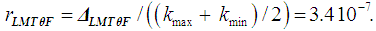 | (26) |
4.3. Avogadro Constant NA
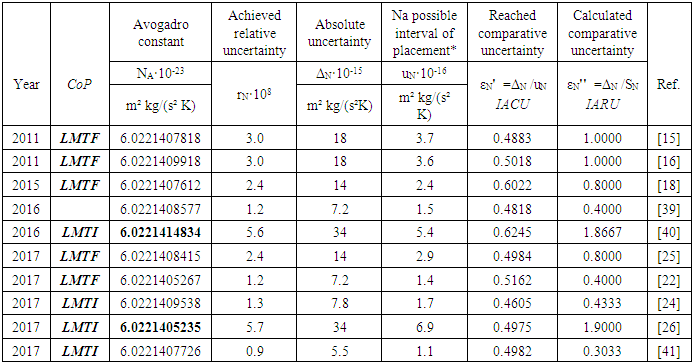
- The Avogadro constant, NA, is the physical constant that connects microscopic and macroscopic quantities, and is indispensable especially in the field of chemistry. In addition, the Avogadro constant is closely related to the fundamental physical constants, namely, the electron relative atomic mass, fine-structure constant, Rydberg constant, and Planck constant. During the period 2011 to 2017, several scientific publications were analyzed, based on the available relative and comparative uncertainty values [15, 16, 18, 22, 24-26, 39-41], and the results are summarized in Table 4.
|
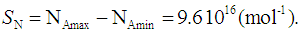 | (27) |
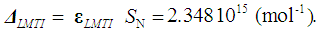 | (28) |
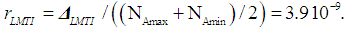 | (29) |
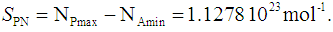 | (30) |
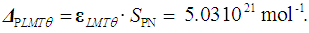 | (31) |
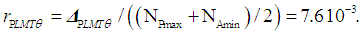 | (32) |
5. Discussion and Conclusions
- The proposed information approach makes it possible to calculate the absolute minimum uncertainty in the measurement of the investigated quantity of the phenomenon using formula (13). The calculation of the recommended relative uncertainty is a useful consequence of the formulated μ-hypothesis and is presented for application in calculating the relative uncertainty of measurement of various physical constants.The information-oriented approach, in particular, IARU, makes it possible to calculate with high accuracy the relative uncertainty, which is in good agreement with the recommendations of CODATA. The principal difference of this method, in comparison with the existing statistical and expert methodology of CODATA, is the fact that the information method is theoretically justified.Significant differences in the values of the comparative uncertainties achieved in the experiments and calculated in accordance with the IACU can be explained as follows. The very concept of comparative uncertainty, within the framework of the information approach, assumes an equally probable account of various variables, regardless of their specific choice by scientists when formulating a model for measuring a particular fundamental constant. Based on their experience, intuition and knowledge, the researchers build a model containing a small number of quantities, and which, in their opinion, reflects the fundamental essence of the process under investigation. In this case, many phenomena, perhaps not significant, secondary, which characterized by specific quantities, are not taken into account. For example, when measuring a value of Planck constant by the LNE Kibble balance (CoPSI≡ LMТI), located inside and shielded, temperature (base quantity is θ) and humidity are controlled, and the air (base quantity is F) density is calculated [26]. Thus, the possible influence of temperature and the use of other type of gas, for example, inert gas, are neglected by developers. In this case, we get a paradoxical situation. On one side, different groups of scientists dealing with the problem of measuring a certain fundamental constant and using the same method of measurement "learn" from each other and improve the test stand to reduce uncertainties known to them. This is clearly seen using the IARU method: when measuring h, k, NA, all the comparative uncertainties are very consistent, especially for measurements made in recent years. However, ignoring a large number of secondary factors, which are neglected by experimenters, leads to a significant variance in the comparative uncertainties calculated by the IACU method.Although the goal of our work is to obtain a fundamental restriction on the measurement of fundamental physical constants, we can also ask whether it is possible to reach this limit in a physically well-formulated model. Since our estimation is given by optimization in comparison with the achieved comparative uncertainty and the observation interval, it is clear that in the practical case, the limit cannot be reached. This is due to the fact that there is an unavoidable uncertainty of the model. It implies the initial preferences of the researcher, based on his intuition, knowledge and experience, in the process of his formulation. The magnitude of this uncertainty is an indicator of how likely it is that your personal philosophical inclinations will affect the outcome of this process. When a person mentally builds a model, at each stage of its construction, there is some probability that the model will not match this phenomenon with a high degree of accuracy.Our framework is not limited to measuring the fundamental physical constants: all considerations within our framework are purely informational theoretically in nature and apply to any models of experimental physics and technology.It would seem, on the side of the CODATA scientists - the ability to analyze and extensive knowledge. Why does the real results of the information method allow you to go the other way? The most important reason is that the analysis is based on factual data, based on a theoretically grounded approach, rather than biased, statistically expert, motivated by any beliefs or preferences. Also, the facts necessary for scientific analysis simply appeared only in recent years. Yes, there was no precedent such that the amateur suddenly presented a theoretically grounded approach based on information theory. This was in 2015 for the first time. An information-oriented approach leads us to the following conclusions. If the mathematics and physics that describe the surrounding reality are effective human creations, then we must take into account the relationship between human consciousness and reality. In addition, the ultimate limits of theoretical, computational, experimental and observational methods, even using the best computers and the most complex experiments, such as the Large Hadron Collider, are limited to the μ-hypothesis applicable to any human activity. Undoubtedly, the current unprecedented scientific and technological progress will continue. However, since the limit for this advance exists, the speed of discoveries is slowed down. This remark is especially important for artificial intelligence, which seeks to create a truly super intelligent machine.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML