| [1] | A. S. Nguetcho Tchakoutio, J. R. Bogning, D. Yemele and T. C. Kofané, “Kink compactons in models with parametrized periodic double-well and asymmetric substrate potentials”, Chaos, Solitons & Fractals, vol. 21, no 1, pp. 165-176, 2004. |
| [2] | D. J. Srolovitz and P. S. Lomdahl “Dislocation dynamics in the 2-D Frenkel-Kontorova model”, Physica D: Nonlinear Phenomena, vol. 23, no 1-3, p p. 402-412, 1986. |
| [3] | S. B. Yamgoué, J. R. Bogning, A. Kenfack Jiotsa and T. C. Kofané “Rational harmonic balance-based approximate solutions to nonlinear single-degree-of-freedom oscillator equations”, Physica Scripta, vol. 81, no 3, p. 035003, 2010. |
| [4] | Tian Bo, G. M. Wei, Zhang Chun-Yi, et al. “Transformations for a generalized variable-coefficient Korteweg–de Vries model from blood vessels, Bose–Einstein condensates, rods and positons with symbolic computation”, Physics Letters A, vol. 356, no 1, p p. 8-16, 2006. |
| [5] | J.R. Bogning, A.S. Tchakoutio Nguetcho and T. C. Kofané “Gap solitons coexisting with bright soliton in nonlinear fiber arrays” International Journal of Nonlinear Sciences and Numerical Simulations Vol. 6(4), pp.339-342, 2005. |
| [6] | J. R. Bogning and T. C. Kofané “Multi-instability of Gap solitons and dynamics of nonlinear excitations in the array of optical fibers” Chaos, Solitons and Fractals Vol. 27, 377-385, 2006. |
| [7] | J. R. Bogning and T. C. Kofané “Analytical Solutions of the discrete nonlinear Schrödinger equations in arrays of optical fibers” Chaos, Solitons and Fractals vol. 28, pp.148-153, 2006. |
| [8] | J. R. Bogning, S. B. Yamgoué and T. C. Kofané, “Effects of torque on the solitons and instantaneous gap solitons in periodically twisted birefringent optical fibers”, Far East journal of Dynamical system, Vol. 11, No.3, pp. 237-250, 2009. |
| [9] | Kuang, Yang (ed.). Delay differential equations: with applications in population dynamics. Academic Press, 1993. |
| [10] | L. A. Lipsitz and A. L. Goldberger, “Loss of 'complexity' and aging: Potential applications of fractals and chaos theory to senescence”, Jama, vol. 267, no 13, p p. 1806-1809, 1992. |
| [11] | V. A. Brazhnyi and V. V. Konotop, “Stable and unstable vector dark solitons of coupled nonlinear Schrödinger equations: Application to two-component Bose-Einstein condensates”, Physical Review E, vol. 72, no 2, p. 026616, 2005. |
| [12] | V. E. Zakharov, and A. B. Shabat, “A scheme for integrating the nonlinear equations of mathematical physics by the method of the inverse scattering problem. I”, Functional analysis and its applications, vol. 8, no 3, p p. 226-235, 1974. |
| [13] | Z. Jie-Fang and C. Feng-Juan, «Abundant Multisoliton Structures of the Generalized Nizhnik–Novikov–Veselov Equation”, Communications in Theoretical Physics, vol. 38, no 4, p. 395, 2002. |
| [14] | L. Senyue and H. Xingbiao, «Broer-Kaup systems from Darboux transformation related symmetry constraints of Kadomtsev-Petviashvili equation”, Communications in theoretical physics, vol. 29, no 1, p. 145, 1998. |
| [15] | F. A. En-Gui, “Solving Kadomtsev–Petviashvili Equation via a New Decomposition and Darboux Transformation”, Communications in Theoretical Physics, vol. 37, no 2, p p. 145-, 2002. |
| [16] | A. M. Wazwaz, “Multiple-soliton solutions for the KP equation by Hirota’s bilinear method and by the tanh–coth method”, Applied Mathematics and Computation, vol. 190, no 1, p p. 633-640, 2007. |
| [17] | J. Hietarinta, “Introduction to the Hirota bilinear method. In: Integrability of Nonlinear Systems”, Springer, Berlin, Heidelberg, pp. 95-103,1997. |
| [18] | S. Y. Lou and H. C. Ma, « Non-Lie symmetry groups of (2+ 1)-dimensional nonlinear systems obtained from a simple direct method”, Journal of Physics A: Mathematical and General, vol. 38, no 7, p. 129, 2005. |
| [19] | W. Oevel and W.H. Steeb, “Painlevé analysis for a time-dependent Kadomtsev-Petviashvili equation”, Physics Letters A, vol. 103, no 5, p p. 239-242, 1984. |
| [20] | J. Weiss, “Modified equations, rational solutions, and the Painlevé property for the Kadomtsev–Petviashvili and Hirota–Satsuma equations”, Journal of mathematical physics, vol. 26, no 9, p p. 2174-2180, 1985. |
| [21] | C. T. Djeumen Tchaho, J. R. Bogning and T. C. Kofané, “Multi-Soliton Solutions of the Modified Kuramoto-Sivashinsky’s Equation by the BDK Method”, Far East Journal of Dynamical Systems, Vol.15, pp. 83 – 98, 2011. |
| [22] | C. T. Djeumen Tchaho, J. R. Bogning and T. C. Kofané, “Modulated Soliton Solution of the Modified Kuramoto-Sivashinsky's Equation”, American Journal of Computational and Applied Mathematics, Vol. 2, pp. 218-224, 2012. |
| [23] | J. R. Bogning, C. T. Djeumen Tchaho and T. C. Kofané, “Construction of the soliton solutions of the Ginzburg-Landau equations by the new Bogning-Djeumen Tchaho-Kofané method”, Physica Scripta, Vol. 85, pp. 025013-025018, 2012. |
| [24] | J. R. Bogning, C. T. Djeumen Tchaho and T. C. Kofané, “Generalization of the Bogning-Djeumen Tchaho-Kofané method for the construction of the solitary waves and the survey of the instabilities”, Far East Journal of Dynamical systems, Vol. 20, No. 2, pp.101-119, 2012. |
| [25] | J. R. Bogning, C. T. Djeumen Tchaho and T. C. Kofané, “Solitary wave solutions of the modified Sasa- Satsuma nonlinear partial differential equation”, American Journal of Computational and Applied Mathematics, Vol. 3, No. 2, pp. 97-107, 2013. |
| [26] | J. R. Bogning, “Pulse soliton solutions of the modified KdV and Born-Infeld equations”, International Journal of Modern Nonlinear Theory and Application, vol.2, pp.135-, 2013. |
| [27] | J. R. Bogning, “N th Order Pulse Solitary Wave Solution and Modulational Instability in the Boussinesq Equation”, American Journal of Computational and Applied Mathematics, vol. 5, no 6, p p. 182-188, 2015. |
| [28] | J. R. Bogning, K. Porsezian, G. Fautso Kuiaté, H. M. Omanda, “Gap solitary pulses induced by the modulational instability and discrete effects in array of inhomogeneous optical fibers”, Physics Journal, Vol.1. No. 3, pp. 216-224, 2015. |
| [29] | J. R. Bogning, “Sech^{n} solutions of the generalized and modified Rosenau-Hyman equations, Asian Journal of Mathematics and Computer Research, vol. 9(1), pp. 1-7, 2016. |
| [30] | J. R. Bogning, “Nth order pulse solitary wave solution and modulational instability in the Boussinesq equation”, American Journal of Computational and Applied Mathematics, 5(6), pp. 182-188, 2015. |
| [31] | R. Njikue, J. R. Bogning and T. C. Kofané, “Exact bright and dark solitary wave solutions of the generalized higher-order nonlinear Schrödinger equation describing the propagation of ultra-short pulse in optical fiber”, Vol. 2, pp. 025030-025038, 2018. |
| [32] | G. Tiague Takongmo and J.R. Bogning, “Construction of Solutions in the shape (pulse; pulse) and (kink; kink) of a set of two equations modeled in a nonlinear inductive electrical line with crosslink capacitor”, American Journal of Circuits, Systems and Signal Processing vol. 4(2), pp. 28-35, 2018. |
| [33] | G. Tiague Takongmo and J.R. Bogning, “Construction of Solitary wave solutions of modeled equations in a nonlinear hybrid electrical line” American Journal of Circuits, Systems and Signal Processing, vol. 4(1), pp. 8-14, 2018. |
| [34] | G. Tiague Takongmo and J.R. Bogning, “Solitary wave solutions of modeled equations in a nonlinear capacitive electrical line”, American Journal of Circuits, Systems and Signal Processing, vol. 4(2), pp. 15-22, 2018. |
| [35] | G. Tiague Takongmo and J.R. Bogning, “Construction of Solitary wave solutions of higher-order nonlinear partial differential equations modeled in a modified nonlinear Noguchi Electrical”, American Journal of Circuits, Systems and Signal Processing, vol. 4(3), pp. 36-44, 2018. |
| [36] | B. B. Kadomtsev, V. I. Petviashvili, "On the stability of solitary waves in weakly dispersive media". Sov. Phys. Dokl. Vol.15, pp. 539-541, 1970. |
| [37] | A. M. Wazwaz, Two forms of (3+1)-dimensional B-type Kadomtsev–Petviashvili equation: multiple soliton solutions. Physica Scripta, vol. 86, no 3, pp. 035007-, 2012. |
| [38] | J. R. Bogning, “Mathematics for nonlinear Physics: Solitary wave in the center of the resolution of dispersive nonlinear partial differential equations”, Book in press, 2018. |



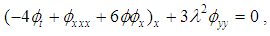
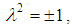 originate from a 1970 paper by two soviet physicists, Boris Kadomtsev (1928-1998) and Vladimir Petviashvili (1936-1993). The two researchers derived the equation that now bears their name as a model to study the evolution of long ion-acoustic waves of small amplitude propagating in plasma under the long transverse perturbations. In the absence of transverse dynamics, this problem is described by the Korteweg-de Vries (KdV) equation. The KP equation was soon widely accepted as a natural extension of classic KdV equation in two spatial dimensions, and was later derived as model for surface and internal water waves by Ablowitz and Segur (1979), and in nonlinear optics by Pelinovsky, Stepanyants and Kivshar (1995), as well as in other physical settings.The focus of the 1970 paper was on a particular problem, the stability of solitons of KdV equation with respect to transverse perturbations. The authors showed that the KdV solitons are stable to such perturbations in the case of media characterized by negative dispersion (that when the phase speed of infinitesimal perturbation decreases with the wave number), in opposite case of positive dispersion media (where the phases speed increases with the wave number).The B-type (3+1)-dimensional Kadomtsev Petviashvili equations are given by [37]
originate from a 1970 paper by two soviet physicists, Boris Kadomtsev (1928-1998) and Vladimir Petviashvili (1936-1993). The two researchers derived the equation that now bears their name as a model to study the evolution of long ion-acoustic waves of small amplitude propagating in plasma under the long transverse perturbations. In the absence of transverse dynamics, this problem is described by the Korteweg-de Vries (KdV) equation. The KP equation was soon widely accepted as a natural extension of classic KdV equation in two spatial dimensions, and was later derived as model for surface and internal water waves by Ablowitz and Segur (1979), and in nonlinear optics by Pelinovsky, Stepanyants and Kivshar (1995), as well as in other physical settings.The focus of the 1970 paper was on a particular problem, the stability of solitons of KdV equation with respect to transverse perturbations. The authors showed that the KdV solitons are stable to such perturbations in the case of media characterized by negative dispersion (that when the phase speed of infinitesimal perturbation decreases with the wave number), in opposite case of positive dispersion media (where the phases speed increases with the wave number).The B-type (3+1)-dimensional Kadomtsev Petviashvili equations are given by [37]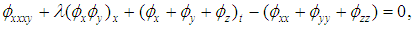
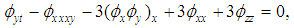
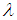 is a real constant. The main objective in this work is to establish the conditions which verified the coefficients
is a real constant. The main objective in this work is to establish the conditions which verified the coefficients 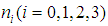 and
and 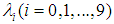 such that the following (3+1) B-type Kadomtsev Petviashvili family equations defined as
such that the following (3+1) B-type Kadomtsev Petviashvili family equations defined as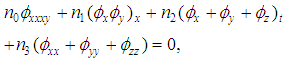
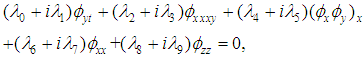
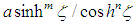 in certain classes of NPDEs, where
in certain classes of NPDEs, where 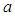 is a real or complex and
is a real or complex and 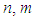 the real constants. This method is focused on the construction of solitary wave solution. It has been adopted to facilitate the resolution or the construction of certain types of nonlinear partial differential equations where the nonlinear terms and dispersive terms coexist. It is also devoted to the construction of the solitary wave solutions of certain categories of NPDEs of the form
the real constants. This method is focused on the construction of solitary wave solution. It has been adopted to facilitate the resolution or the construction of certain types of nonlinear partial differential equations where the nonlinear terms and dispersive terms coexist. It is also devoted to the construction of the solitary wave solutions of certain categories of NPDEs of the form 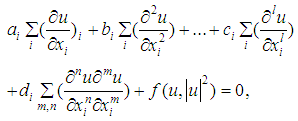
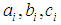 and
and 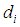 are constants that characterize partial differential equations,
are constants that characterize partial differential equations, 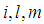 and
and 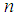 positive natural integers,
positive natural integers, 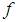 a linear arbitrary function of
a linear arbitrary function of 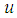 and
and 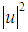 , and
, and 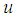 the unknown function to determine and
the unknown function to determine and 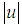 the magnitude of
the magnitude of 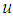 . We look for the solution of equation (6) under the form of linear combination of the hyperbolic function as follows
. We look for the solution of equation (6) under the form of linear combination of the hyperbolic function as follows 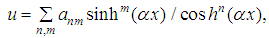
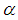 is constant which depends on the parameter of the system which models NPDE and
is constant which depends on the parameter of the system which models NPDE and 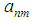 the constants to be determined. Introducing the Bogning function defined by
the constants to be determined. Introducing the Bogning function defined by 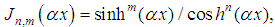
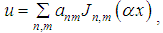
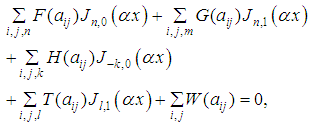
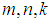 and
and 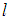 are the positive whole integers.Setting the coefficients
are the positive whole integers.Setting the coefficients 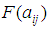 ,
, 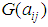 ,
, 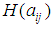 ,
, 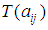 and
and 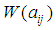 to zero we obtain the coefficient equations then, the resolution permits to determine the coefficients
to zero we obtain the coefficient equations then, the resolution permits to determine the coefficients 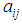 .
. 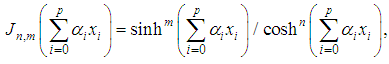
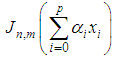 represents the implicit form of the function,
represents the implicit form of the function, 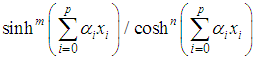 the explicit form of the function,
the explicit form of the function, 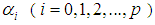 represent the parameters associated to the independent variables
represent the parameters associated to the independent variables 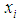 (
(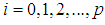 ), the couple
), the couple 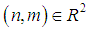 indicate the power of the function. In a more precise way,
indicate the power of the function. In a more precise way, 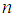 is the power of
is the power of 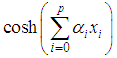 and
and 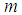 the power of
the power of 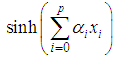 . In dimension one; it is defined and according to the choice of the constant of anybody by
. In dimension one; it is defined and according to the choice of the constant of anybody by 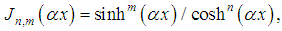
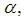 represents the parameter associated with the independent variable
represents the parameter associated with the independent variable 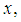 and the couple
and the couple 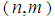 indicates the power of the function.
indicates the power of the function. 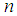 is the power of
is the power of 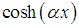 and
and 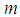 the power of
the power of 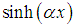 . Some of the main properties of this function we are going to use to solve the equations are given by:
. Some of the main properties of this function we are going to use to solve the equations are given by: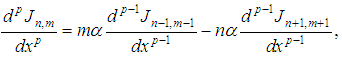
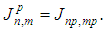
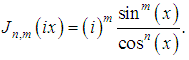
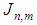 of parameter
of parameter 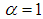 , in order to simplify calculations of the various terms of equation (4), we pose the change of variable
, in order to simplify calculations of the various terms of equation (4), we pose the change of variable 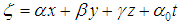 and equation (4) becomes
and equation (4) becomes 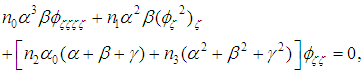
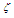 , gives
, gives 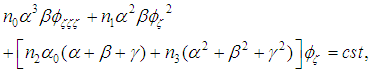
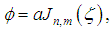
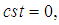 yields to the range equation which is the main equation in the centre of all analysis
yields to the range equation which is the main equation in the centre of all analysis 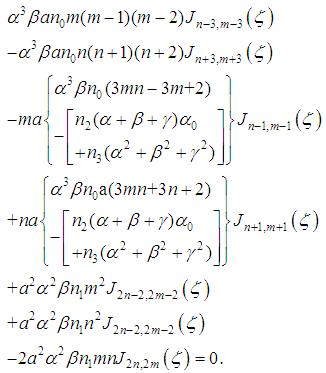
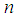 and
and 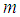 for which certain terms of equation (19) gather are given by
for which certain terms of equation (19) gather are given by 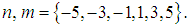 § When
§ When 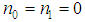 , equation (4) reduces to
, equation (4) reduces to 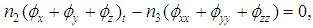
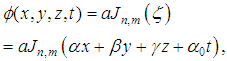
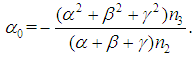
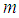 and
and 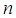 for which certain terms of equation (12) gather are given by
for which certain terms of equation (12) gather are given by 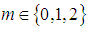 and
and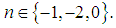 Thus, we observe these cases as follows:§ When
Thus, we observe these cases as follows:§ When 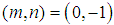 and
and 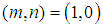 we obtain respectively from equation (19), the following equations
we obtain respectively from equation (19), the following equations 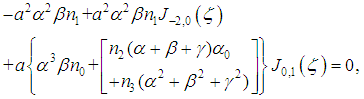
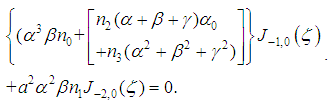
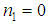 gives
gives 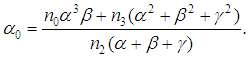
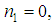 reduces equation (4) as follows
reduces equation (4) as follows 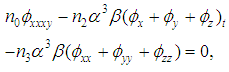
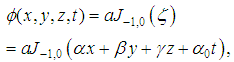
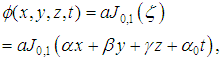
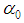 is defined by equation (25). § When
is defined by equation (25). § When 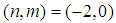 or
or 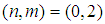 we obtain respectively from equation (19)
we obtain respectively from equation (19) 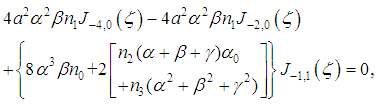
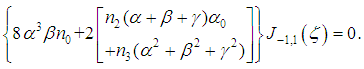
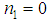 gives
gives 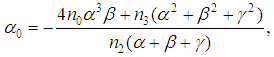
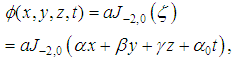
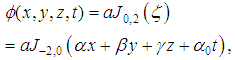
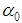 is defined by equation (28). § When
is defined by equation (28). § When 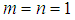 and
and 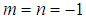 we obtain in that order from equation (19), equations
we obtain in that order from equation (19), equations 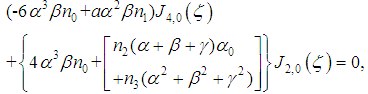
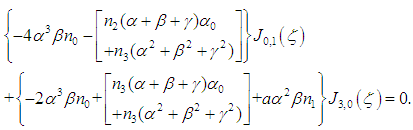
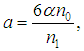
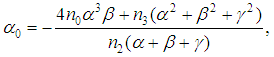
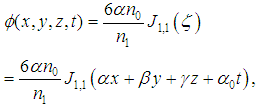
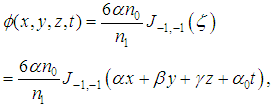
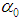 is defined by equation (34).We see that from the different relations linking the constants
is defined by equation (34).We see that from the different relations linking the constants 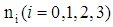 , we can define many equations derived from equation (4) as well as their solutions.
, we can define many equations derived from equation (4) as well as their solutions. 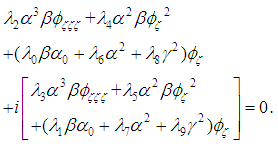
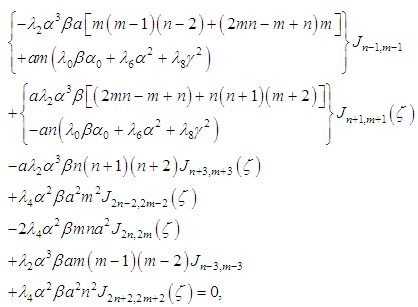
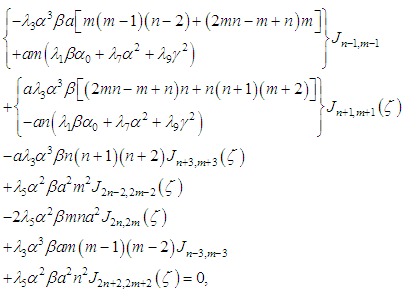
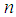 and
and 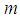 for which certain terms of equations (39) and (40) gather are given by
for which certain terms of equations (39) and (40) gather are given by 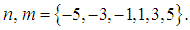 The analysis of the equations (38) and (39) above enables to identify all the possibilities of solutions.§ When
The analysis of the equations (38) and (39) above enables to identify all the possibilities of solutions.§ When 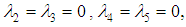
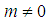 and
and 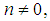 we obtain respectively from equations (38) and (39) the following equations
we obtain respectively from equations (38) and (39) the following equations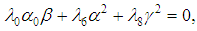
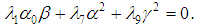
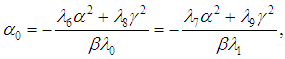
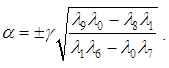
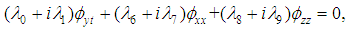
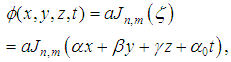
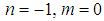 or
or 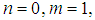 the resolution of equations (38) and (39) impose to set
the resolution of equations (38) and (39) impose to set 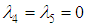 and obtain the constants given by
and obtain the constants given by 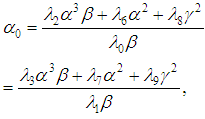
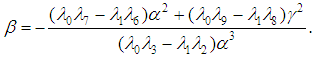
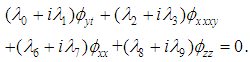
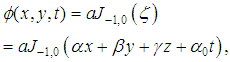
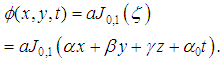
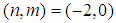 or
or 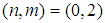 , we obtain from equations (38) and (39) the constraint
, we obtain from equations (38) and (39) the constraint 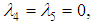 such that
such that 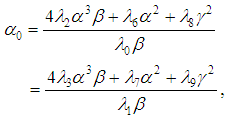
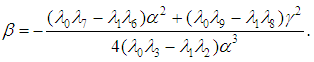
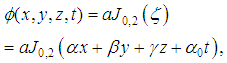
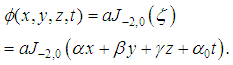
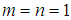 and
and 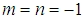 we find from equations (38) and (39) that
we find from equations (38) and (39) that 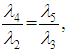
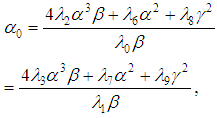
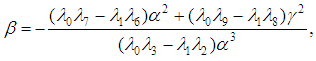
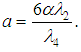
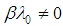 ,
, 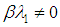 ,
, 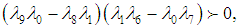
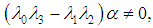
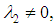
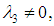
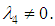 With the above conditions, equation (5) reduces to
With the above conditions, equation (5) reduces to 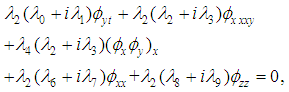
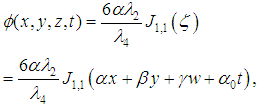
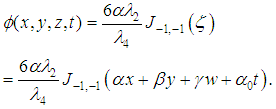
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML