-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2018; 8(4): 70-79
doi:10.5923/j.ajcam.20180804.02

Novel Method for Calculating the Measurement Relative Uncertainty of the Fundamental Constants
Boris Menin
Mechanical & Refrigeration Consultation Expert, Beer-Sheba, Israel
Correspondence to: Boris Menin , Mechanical & Refrigeration Consultation Expert, Beer-Sheba, Israel.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Heisenberg's 90-year-old tenet on uncertainties in physics asserts that, in nature, determination of the accuracy of coordinates and momentum of any material object has a fundamental limit. Besides, Planck's constant is vanishingly small, with respect to macro bodies, and hence cannot be used for practical applications. In this paper, the author proposes another novel limit, based on the concept that every model contains a certain amount of information about the object under study, and hence it must have optimal number of selected quantities. The author demonstrates how, by the usual measurements of fundamental physical constants, the proposed novel limit can be applied to estimate the permissible absolute and relative uncertainties of the metric being measured. For this, the author used the information theory for giving a theoretical explanation and for grounding of the experimental results, which determine the precision of different fundamental constants. It is shown that this new fundamental limit, characterizing the discrepancy between a model and the observed object, cannot be overcome by any improvement in measuring instruments, mathematical methods or super-powerful computers.
Keywords: Computational modelling, Information theory, Measurement of fundamental physical constants, Theory of measurements, Theory of similarity
Cite this paper: Boris Menin , Novel Method for Calculating the Measurement Relative Uncertainty of the Fundamental Constants, American Journal of Computational and Applied Mathematics , Vol. 8 No. 4, 2018, pp. 70-79. doi: 10.5923/j.ajcam.20180804.02.
Article Outline
1. Basic Thesis
- Modeling is an information process through which information about a state and the behaviour of an observed object is obtained from the developed model. This information is the main subject of interest in modeling theory [1]. Let a specific object under investigation be considered. The modeller, during a thought experiment (the distortion is not brought in a real system) chooses, according to his or her knowledge, intuition and experience, specific quantities that characterize a studied process. The choice of set of quantities is constrained not only by the possible duration of the study and its permitted cost. The main problem of the modeling process is that the observer selects quantities from a vast but finite set of quantities that are defined within, for example, the International System of Units (SI). When modeling a physical phenomenon, one group of scientists may choose quantities that may substantially differ from those chosen by another group, as happened, for example, during the study of electrons that behave like particles or waves. That is why SI can be characterized by equally probable accounting of any quantity chosen by the modeler. The SI includes seven base quantities: L- length, M– mass, Т– time, I– electric current,
 thermodynamic temperature, J– force of light and F– amount of substance [2]. SI has the consensus of the scientists. Besides, modeling of the phenomena is impossible without SI, which is considered the basis of people’s knowledge about the nature surrounding them. SI includes the base and the derived quantities used for describing different classes of phenomena (CoP). For example, in SI mechanics, there a basis used is {L– length, M– mass and Т– time}, i.e. CoPSI ≡ LMT. It is known [3] that the dimension of any derived quantity can be expressed as a unique function of the product of base quantities with certain exponents, i.e., l... f, which can take only integer values and change over specific ranges:
thermodynamic temperature, J– force of light and F– amount of substance [2]. SI has the consensus of the scientists. Besides, modeling of the phenomena is impossible without SI, which is considered the basis of people’s knowledge about the nature surrounding them. SI includes the base and the derived quantities used for describing different classes of phenomena (CoP). For example, in SI mechanics, there a basis used is {L– length, M– mass and Т– time}, i.e. CoPSI ≡ LMT. It is known [3] that the dimension of any derived quantity can be expressed as a unique function of the product of base quantities with certain exponents, i.e., l... f, which can take only integer values and change over specific ranges: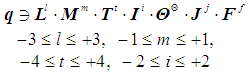 | (1) |
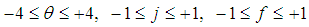 | (2) |
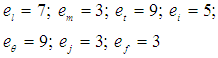 | (3) |
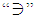 means "corresponds to a dimension"; еl, …, еf denote the numbers of choices of dimensions for each base quantity. For example, L-3 is used in a formula of density, and
means "corresponds to a dimension"; еl, …, еf denote the numbers of choices of dimensions for each base quantity. For example, L-3 is used in a formula of density, and 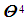 in the Stefan-Boltzmann law. Because SI is an Abelian finite group [4, 5] with the natural structure of a module over the ring of integers, the exponents of the base quantities in formula (1) for SI take only integer values! Thankfully, because of this fact, and considering (1) - (3) and the π-theorem [6], the total number of possible dimensionless criteria µSI of SI could be calculated
in the Stefan-Boltzmann law. Because SI is an Abelian finite group [4, 5] with the natural structure of a module over the ring of integers, the exponents of the base quantities in formula (1) for SI take only integer values! Thankfully, because of this fact, and considering (1) - (3) and the π-theorem [6], the total number of possible dimensionless criteria µSI of SI could be calculated 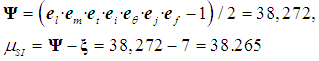 | (4) |
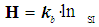 | (5) |
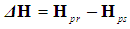 | (6) |
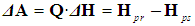 | (7) |
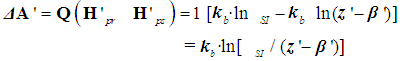 | (8) |
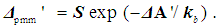 | (9) |
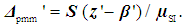 | (10) |
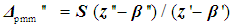 | (11) |
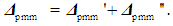 | (12) |
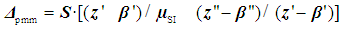 | (13) |
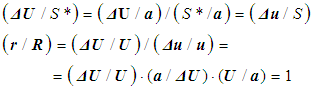 | (14) |
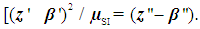 | (15) |
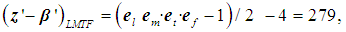 | (16) |
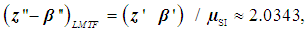 | (17) |
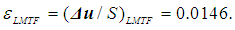 | (18) |
2. Applications
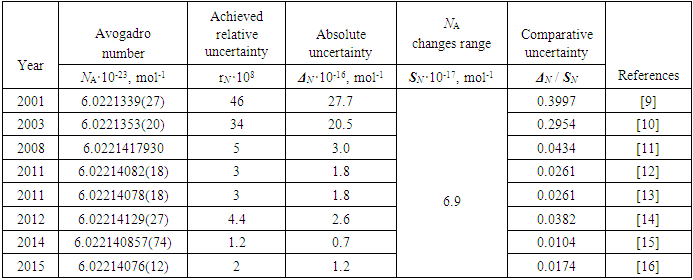
2.1. Avogadro Number NA
- During the period 2001 to 2015, several scientific publications were analyzed, based on the available relative and comparative uncertainty values [9-16], and the results are summarized in Table 1. In order to apply a stated approach, an estimated observation interval of the Avogadro number is chosen as the difference in its values obtained from the experimental results of two projects: Namin = 6.0221339(27)·1023 mol-1 [9] (De Bievre et al., 2001) and Namax = 6.022140857(74)·1023 mol-1 [15].
|
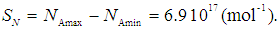 | (19) |
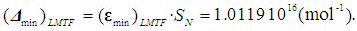 | (20) |
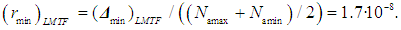 | (21) |
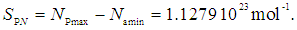 | (22) |
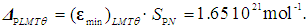 | (23) |
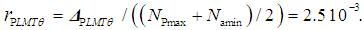 | (24) |
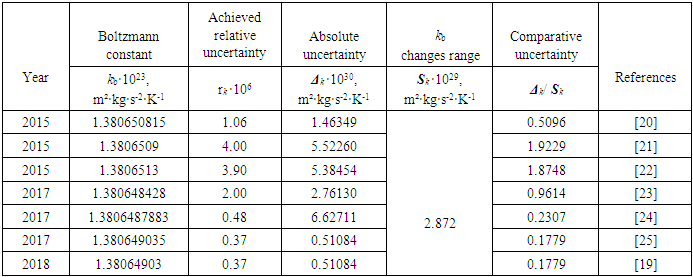
2.2. Boltzmann Constant kb
- A detailed analysis of the measurements of Boltzmann’s constant, made since 1973 is available in [19]. The more recent of these measurements, made during 2015-2018 [19-25], were analyzed for this study. In order to apply a stated approach, an estimated observation interval of kb is chosen as the difference in its values obtained from the experimental results of two projects: kbmax = 1.3806513·10-23 m²·kg·s-2·K-1 [22] and kbmin = 1.380648428·10-23 m²·kg·s-2·K-1 [2]. In this case, the possible observed range Sk of kb variation is equal to:
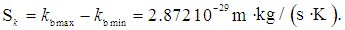 | (25) |
|
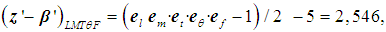 | (26) |
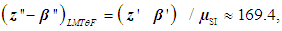 | (27) |
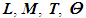 and F; division by 2 indicates that there are direct and inverse quantities, e.g. L1 is the length and L-1 is the run length. The object can be judged based on the knowledge of only one of its symmetrical parts, while the other parts that structurally duplicate this part may be regarded as information-empty. Therefore, the number of options of dimensions may be reduced by 2 times. According to (13), (26) and (27),
and F; division by 2 indicates that there are direct and inverse quantities, e.g. L1 is the length and L-1 is the run length. The object can be judged based on the knowledge of only one of its symmetrical parts, while the other parts that structurally duplicate this part may be regarded as information-empty. Therefore, the number of options of dimensions may be reduced by 2 times. According to (13), (26) and (27), 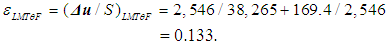 | (28) |
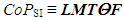 is given by the following:
is given by the following: 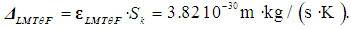 | (29) |
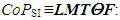
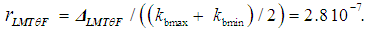 | (30) |
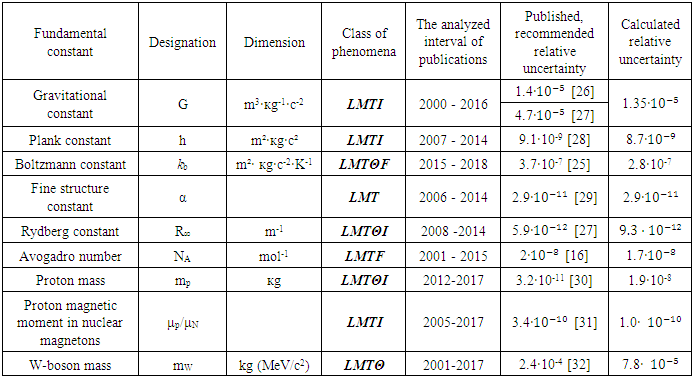
2.3. Summarized Data
- Following an analogous procedure, the measurement results for the Planck constant, the fine structure constant, the Rydberg constant, the Avogadro number, the mass of a proton, the proton magnetic moment, in nuclear magnetons and W-boson mass were analyzed and the results summarized in Table 3 [16, 25-32]. The discrepancy between the published and the calculated values of relative uncertainty could be because of insufficient volume of data, which can be overcome by the author in his future work. Another reason is the need to improve experimental test benches. It is necessary to hope for the best: the continuation of the financing of experimental research, but the ideas for improving measurement methods never end.
|
3. Discussion and Conclusions
- The proposed information approach has its own implications. Any physical process, from quantum mechanics to palpitation, can be viewed by the observer only through the idiosyncratic "lens." Its material is a combination of not only mathematical equations, but also of the researcher's desire, intuition, experience and knowledge. These, in turn, are framed by SI, which is chosen with the consensus of the researchers. Thus, a sort of aberration—distortion of reality—creeps into modeling, prior to the formulation of any physical, or even, mathematical statement. The degree of distortion of the image in comparison with the actual process depends essentially on the chosen class of phenomena and the number of the “quantities created by observation” [36]. The accuracy of the model of any physical phenomena can no longer be considered limited by the boundaries, determined by the Heisenberg uncertainty relation. “Potential accuracy of the measurement” [17] is limited by the initially known unrecoverable comparative uncertainty determined by the μ-hypothesis and depending on the class of phenomena and the number of quantities chosen by the strong-willed researcher. This is where equation (13) can be considered a kind of compromise solution between future possibilities, limitations in improving measuring devices, diversity in mathematical calculation methods, and the increasing power of computers.Under the unrecoverable uncertainty of the model, we mean the initial preferences of the researcher, based on his intuition, knowledge and experience, in the process of its formulation. The magnitude of this uncertainty is an indicator of how likely it is that one's personal philosophical leanings will affect the outcome of this process. Therefore, modeling, like any information process, looks like any similar process in nature - noisy, with random fluctuations, in our case, an equiprobable choice of quantities that depends on the observer. When a person mentally builds a model, at each stage of its construction there is some probability that the model will not match the phenomenon to a high degree of accuracy.The quality of the scientific hypothesis should be judged not only by its correspondence to empirical data, but also by its predictions. In this study, information theory was used to give a theoretical explanation and grounding of the experimental results, which determine the precision of different fundamental constants. A focus on the real is what allows the information measure approach to explore new avenues in the different physical theories and technologies. The approach proposed here can answer one fundamental question - how we are seeing? - because it is based on the fundamental subject, namely the International system of units. The information approach allows for crafting of a meaningful picture of future results, because it is based on the realities of the present. In this sense, when applying the results of precision research to the limitations that constrain modern physics, it is necessary to clearly understand the research framework and the way the original data can be modified [34]. This can be considered as an additional reason for speedy implementation of the μSI - hypothesis, the concept of SI and, in general, the information approach for analyzing existing experimental data on the measurement of fundamental physical constants. The experimental physics segment is expected to be the most rewarding application for the information method, thanks to a greater demand for high accuracy measurements. The proposed information approach allows for calculating the absolute minimum uncertainty of the measurement of the investigated quantity of the phenomenon, using formula (13). Calculation of the recommended relative uncertainty is a useful consequence of the formulated μ-hypothesis and is presented for application in calculation of relative measurement uncertainty of different physical constants.The main purpose of most measurement models is to make predictions, in verifying the true-target magnitude of the researched quantity. The quantity that need to be predicted are generally not experimentally observable before the prediction, since otherwise no prediction would be needed. Assessing the credibility of such extrapolative predictions is challenging. In validation CODATA's approach, the model outputs for observed quantities are constructed, using modern advanced statistical methods and powerful computers to determine if they are consistent. By itself, this consistency only ensures that the model can predict the measured physical constants under the conditions of the observations [37]. This limitation dramatically reduces the utility of the CODATA effort for decision making because it implies nothing about predictions for scenarios outside of the range of observations. μ-hypothesis proposes and explores a predictive assessment process of the relative uncertainty that supports extrapolative predictions for models of measurement of the fundamental physical constants. The findings of this study are applicable to all the models in physics and engineering including climate, heat- and mass-transfer and theoretical and experimental physics systems in which there is always a trade-off between model’s complexity and the accuracy required. On other side, the proposed method is not claimed to be universally applicable, because it does not answer the question on the selection of specific physical quantities for the best representation of the surrounding world. The information-oriented approach for estimating the model's uncertainty does not involve any spatio-temporal or causal relationship between the quantities involved; instead, it considers only the differences between their numbers. However, it can be firmly asserted that the findings presented here reveal, contrary to what is generally believed, that the precision of physics and engineering devices is fundamentally bounded by certain constraints and cannot be improved to an arbitrarily high degree of accuracy. The outcome of this study, which seems to be too good to be true, indeed turns out to be a real breakthrough.It is now possible to design optimal models, which use the required number of the dimensional quantities that correspond to the selected SBQ, chosen according to engineering and experimental physics considerations.The theory of measurements and its concepts remain the correct science today, in the twenty-first century, and will remain faithful forever (paraphrase of Prof. L.B. Okun [38]. The use of the μSI hypothesis only limits the scope of the measurement theory for uncertainties exceeding the uncertainty in the physical-mathematical model due to its finiteness. The key idea is that, although the basic principles of measurement remain valid, they need to be applied discreetly, depending on the stage of model's computerization.Though the summarized data and explanations to Tables 1-3 appear to confirm the predictive power of the μ-hypothesis, the present author is skeptical of considering them as "confirmation". In fact, the μ-hypothesis is considered a Black Swan [39] among the existing theories related to checking the discrepancy between the model and the observed object, because none of the existing methods for validating and verifying the constructed model takes into account the smallest absolute uncertainty of the model’s measured quantity, caused by the choice of the class of the phenomena and the number of quantities created by observation.“Our knowledge of the world begins not with matter but with perceptions” [40]. According to the μ-hypothesis, there are no physical quantities independent of the observer. Instead, all physical quantities refer to the observer. This is motivated by the fact that, according to the information approach, different observers can take differently account of the same sequence of events. Therefore, each observer assumes to "dwell" in his own physical world, as determined by the context of his own observations.Finally, because the values of comparative uncertainties and the required number of the chosen quantities are completely independent and different for each class of a phenomena, the attained approach can now, in principle, become an arbitrary metric for comparing different models that describe the same recognized object. In this way, the information measure approach will radically alter the present understanding of the modeling process. In conclusion, it must be said that, fortunately or unfortunately, one sees everything in the world around him or her, through a haze of doubts and errors, excepting love and friendship. If you did not know about the μ-hypothesis, you would not come to this conclusion.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML