Md. Babul Hossain, Mousumi Datta
Department of Mathematics, Mawlana Bhashani Science and Technology University, Santosh, Tangail, Bangladesh
Correspondence to: Md. Babul Hossain, Department of Mathematics, Mawlana Bhashani Science and Technology University, Santosh, Tangail, Bangladesh.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this paper we introduced a new method, named Elzaki Substitution Method, which is based on Elzaki transform for solving linear partial differential equations with mixed partial derivatives. This proposed method will play an important role to find exact solutions of partial differential equations involving mixed partial derivatives with less computation as compared with other methods such as Method of Separation of Variables (MSV) and Variation Iteration Method (VIM). Elzaki transforms of partial derivatives with some fundamental properties are presented in this paper. Illustrative examples are presented to demonstrate the effectiveness, efficiency and applicability of proposed method.
Keywords:
Partial differential equations, Exact solution, Elzaki Transform, Elzaki Substitution Method
Cite this paper: Md. Babul Hossain, Mousumi Datta, Solutions of Linear Partial Differential Equations with Mixed Partial Derivatives by Elzaki Substitution Method, American Journal of Computational and Applied Mathematics , Vol. 8 No. 3, 2018, pp. 59-64. doi: 10.5923/j.ajcam.20180803.03.
1. Introduction
Linear partial differential equations involving mixed partial derivatives arise in various fields of physical science, astronomy and engineering. Sometimes it’s very difficult to solve them, either numerically or theoretically. There are various methods such as Method of Separation of Variables, Variation Iteration Method, Laplace Transform, Laplace Substitution Method [7], Sumudu Transform, to solve these kinds of equations. In recent, Tariq Elzaki introduced a new integral transform known as Elzaki transform [1-6] which is modified transform of Sumudu and Laplace transforms. Elzaki transform can be used to solve ordinary differential equations [1], partial differential equations [3, 8], partial integro-differential equations [9, 12], system of partial differential equations [10, 13] and wave equations [8, 15]. The main advantage of Elzaki transform is that it eliminates the need of linearization, perturbation or any other transformation. Elzaki transforms are widely used for solving ordinary and partial differential equations. The existing methods for solving partial differential equations involving mixed partial derivatives are time consuming with large computation. Our proposed method is more powerful and efficient to solve partial differential equations involving mixed partial derivatives with less computation.
2. Preliminaries
2.1. Elzaki Transform
A new transform called the Elzaki transform defined for function of exponential order we consider functions in the set 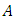 defined by:
defined by: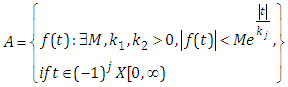 | (2.1) |
In a set 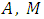 is constant must be finite,
is constant must be finite, 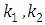 may be finite or infinite.The Elzaki transform is defined by
may be finite or infinite.The Elzaki transform is defined by 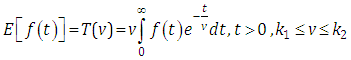 | (2.2) |
In this transform the variable 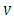 is used to factor the variable
is used to factor the variable 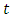 in the argument of function
in the argument of function 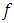 . This transform has deeper connection with the Laplace transform. The aim of this study is to show the applicability of this interesting new transform and its ability in solving the mixed order linear partial differential equations.
. This transform has deeper connection with the Laplace transform. The aim of this study is to show the applicability of this interesting new transform and its ability in solving the mixed order linear partial differential equations.
2.2. Fundamental Properties of Elzaki Transform
Table 1
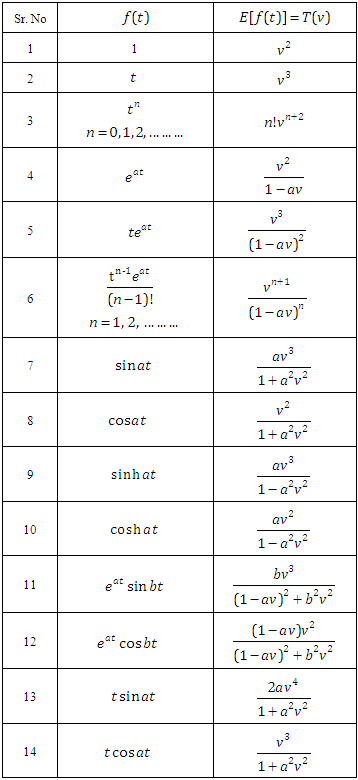 |
| |
|
2.3. Elzaki Transformations of Partial Derivatives
Let 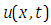 be a function of two independent variables
be a function of two independent variables 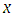 and
and 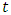 , then
, then 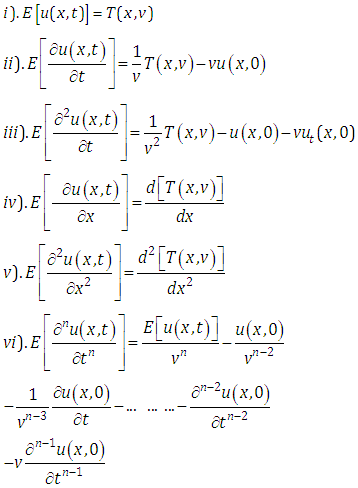
3. Elzaki Substitution Method
The aim of this section is to discuss the Elzaki substitution method. We consider the general form of non-homogeneous partial differential equation with initial conditions is given below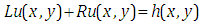 | (3.1) |
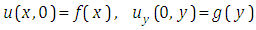 | (3.2) |
Where 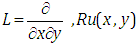 is the remaining linear terms in which contains only first order partial derivatives of
is the remaining linear terms in which contains only first order partial derivatives of 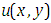 with respect to either
with respect to either 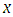 or
or 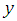 and
and 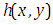 is the source term.We can write equation (3.1) in the following form
is the source term.We can write equation (3.1) in the following form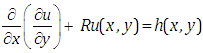 | (3.3) |
Substituting 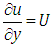 in equation (3.3), we obtain
in equation (3.3), we obtain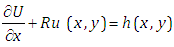 | (3.4) |
Taking Elzaki transform of equation (3.4) with respect to x, we get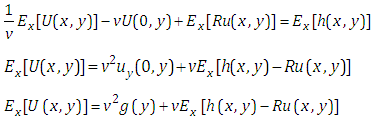 | (3.5) |
Taking inverse Elzaki transform of equation (3.5) with respect to x, we get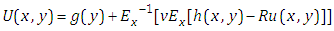 | (3.6) |
Re-substitute the value of 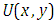 in equation (3.6), we get
in equation (3.6), we get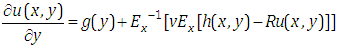 | (3.7) |
This is a first order partial differential equation in the variables x and y.Taking Elzaki transform of equation (3.7) with respect to y, we get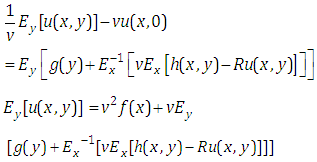 | (3.8) |
Taking the inverse Elzaki transform of equation (3.8) with respect to y, we get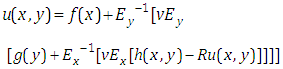 | (3.9) |
The last equation (3.9) gives the exact solution of initial value problem (3.1)
4. Illustrative Examples
To illustrate this method for partial differential equations with mixed partial derivatives we take four examples in this sectionExample 1: Consider the following linear partial differential equation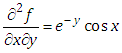 | (4.1) |
with initial conditions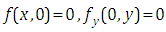 | (4.2) |
In the above initial value problem 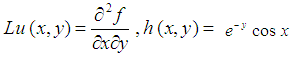 and general linear term
and general linear term 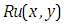 is zero.We can re-write equation (4.1) in the following form
is zero.We can re-write equation (4.1) in the following form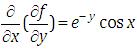 | (4.3) |
Substituting 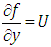 in equation (4.3), we get
in equation (4.3), we get 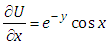 | (4.4) |
which is non-homogeneous partial differential equation of first order.Taking Ezaki transform on both sides of equation (4.4) with respect to x, we get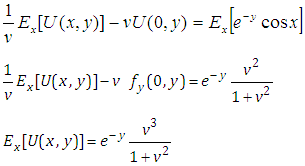 | (4.5) |
Taking inverse Elzaki transform of equation (4.5) with respect to x, we get 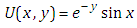
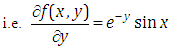 | (4.6) |
which is the partial differential equation of first order in the variables x and y.Taking Elzaki transform of equation (4.6) with respect to y, we get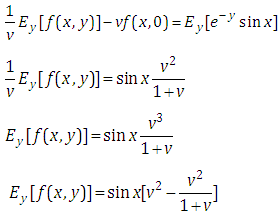 | (4.7) |
Taking inverse Elzaki transform of equation (4.7) with respect to y, we get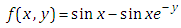 | (4.8) |
This is the required exact solution of equation (4.1). This can be verifying though the substitution.Example 2: Consider the linear partial differential equation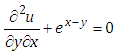 | (4.9) |
With the initial conditions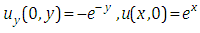 | (4.10) |
Equation (4.10) we can write in the following form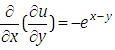 | (4.11) |
Putting 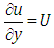 in equation (4.11), we get the non-homogeneous partial differential equation of first order is
in equation (4.11), we get the non-homogeneous partial differential equation of first order is 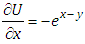 | (4.12) |
Taking Elzaki transform on both sides of equation (4.12) with respect to x, we obtain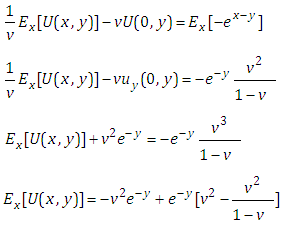 | (4.13) |
Taking inverse Elzaki transform on both sides of equation (4.13) with respect to x, we get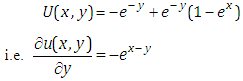 | (4.14) |
Taking Elzaki transform on both sides of equation (4.14) with respect to y, we get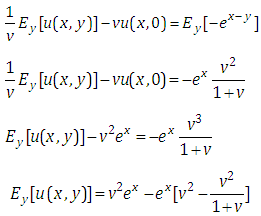 | (4.15) |
Taking inverse Elzaki transform on both sides of equation (4.15) with respect to y, we get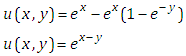 This is the required exact solution of equation (4.9). This can be verifying though the substitution.Example 3: Consider the linear partial differential equation
This is the required exact solution of equation (4.9). This can be verifying though the substitution.Example 3: Consider the linear partial differential equation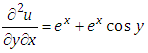 | (4.16) |
with the initial conditions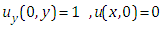 | (4.17) |
We can write the equation (4.16) in the following form as 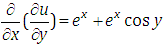 | (4.18) |
Putting 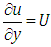 in equation (4.18), we get
in equation (4.18), we get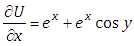 | (4.19) |
This is the non-homogeneous partial equation of first order.Taking Elzaki transform on both sides of equation (4.19) with respect to x, we get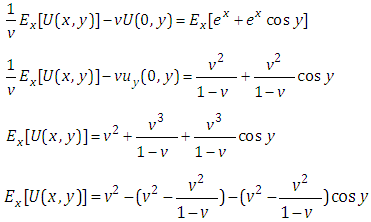 | (4.20) |
Taking inverse Elzaki transform on both sides of equation (4.20) with respect to x, we get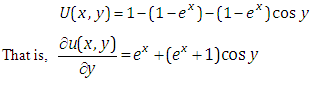 | (4.21) |
Taking Elzaki transform on both sides of equation (4.21) with respect to y, we get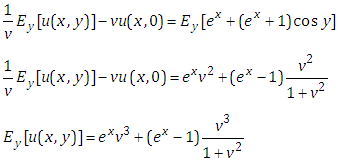 | (4.22) |
Taking inverse Elzaki transform on both sides of equation (4.22) with respect to y, we get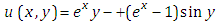 This is the required exact solution of equation (4.16). This can be verifying though the substitution.Example 4: Consider the linear partial differential equation with
This is the required exact solution of equation (4.16). This can be verifying though the substitution.Example 4: Consider the linear partial differential equation with 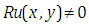
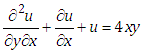 | (4.23) |
With the initial conditions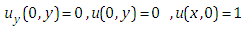 | (4.24) |
Equation (4.23) can be written in the following form as 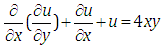 | (4.25) |
Putting 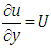 in equation (4.25), we get
in equation (4.25), we get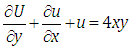 | (4.26) |
Taking Elzaki transform on both sides of equation (4.26) with respect to x, we get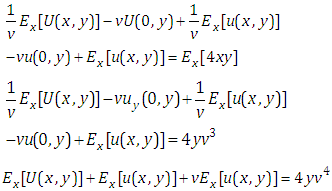 | (4.27) |
Taking inverse Elzaki transform on both sides of equation (4.27) with respect to x, we get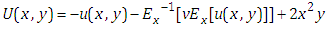 That is,
That is, 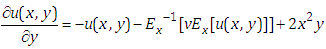 | (4.28) |
Taking Elzaki transform on both sides of equation (4.28) with respect to y, we get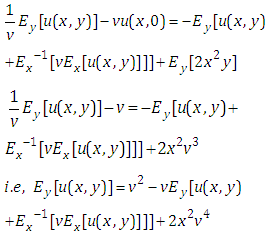 | (4.29) |
Taking inverse Elzaki transform on both sides of equation (4.29) with respect to y, we get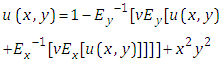 We cannot solve the equation (4.30) because our goal
We cannot solve the equation (4.30) because our goal 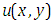 is appeared in both sides of equation (4.30). Thus the equation (4.23) we cannot solve by using Elzaki substitution method because of
is appeared in both sides of equation (4.30). Thus the equation (4.23) we cannot solve by using Elzaki substitution method because of 
5. Conclusions
The main goal of this paper is to find exact solutions of partial differential equations involve mixed partial derivatives with general linear term 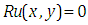 by proposed Elzaki Substitution Method. This result has been extracted that Elzaki Substitution Method plays a key role in finding the solution of higher order initial value problem which involves the mixed partial derivatives with general linear term
by proposed Elzaki Substitution Method. This result has been extracted that Elzaki Substitution Method plays a key role in finding the solution of higher order initial value problem which involves the mixed partial derivatives with general linear term 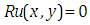 . The operation of this method is simple in use and time saving. But the result of example number four tell us that Elzaki Substitution Method is not applicable for those partial differential equations in which
. The operation of this method is simple in use and time saving. But the result of example number four tell us that Elzaki Substitution Method is not applicable for those partial differential equations in which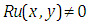 . Consequently the Elzaki Substitution Method can be applied for other equations that performing in various scientific fields.
. Consequently the Elzaki Substitution Method can be applied for other equations that performing in various scientific fields.
References
| [1] | Elzaki, T.M., 2011. The new integral transforms “Elzaki Transform”. Global Journal of Pure and Applied Mathematics, 7(1), pp.57-64. |
| [2] | Elzaki, T.M., 2012. On the New Integral Transform “ELzaki Transform” Fundamental Properties Investigations and Applications. Global Journal of Mathematical Sciences: Theory and Practical, 4(1), pp.1-13. |
| [3] | Elzaki, T.M., 2011. Application of new transform “Elzaki transform” to partial differential equations. Global Journal of Pure and Applied Mathematics, 7(1), pp.65-70. |
| [4] | Elzaki, T.M., 2012. On Some Applications of New Integral Transform ''Elzaki Transform''. The Global Journal of Mathematical Sciences: Theory and Practical, 4(1), pp.15-23. |
| [5] | Elzaki, T.M., 2011. On the connections between Laplace and Elzaki transforms. Advances in Theoretical and Applied Mathematics, 6(1), pp.1-11. |
| [6] | Elzaki, T.M., 2012. Elzaki and Sumudu transforms for solving some differential equations. Global Journal of Pure and Applied Mathematics., 8(2). |
| [7] | Handibag, S. and Karande, B.D., 2012. Laplace substitution method for solving partial differential equations involving mixed partial derivatives. International journal of pure and applied mathematics, 78(7), pp.973-979. |
| [8] | Devi, A., Jakhar, M. And Gill, V., 2018. • Solution of Partial Differential Equations by Elzaki Transform. International Journal of Mathematical Archive EISSN 2229-5046, 9(1). |
| [9] | Arabia, J.S., 2015. Solution of partial integro-differential equations by Elzaki transform method. Applied Mathematical Sciences, 9(6), pp.295-303. |
| [10] | Elzaki, T.M., 2011. On the ELzaki Transform and System of Partial Differential Equations. Advances in Theoretical and Applied Mathematics, 6(1), pp.115-123. |
| [11] | Elzaki, T.M. and Ezaki, S.M., 2011. On the solution of integro-differential equation systems by using Elzaki transform. Global Journal of Mathematical Sciences: Theory and Practical, 3(1), pp.13-23. |
| [12] | Mahgob, M.M.A., 2015. Solution of partial integro-differential equations by double Elzaki transform method. Mathematical Theory and Modeling, 5(5). |
| [13] | Elzaki, T.M. and Elzaki, S.M., 2012. On the Tarig transform and system of partial differential equations. Applied Mathematics, Elixir Appl. Math, 42, pp.6373-6376. |
| [14] | Alshikh, A.A. and AbdelrahimMahgoub, M.M., 2016. A Comparative Study Between Laplace Transform and Two New Integrals. ELzaki” Transform and “Aboodh” Transform,” Pure and Applied Mathematics Journal2016, 5(5), pp.145-150. |
| [15] | Hussain, F., 2017. Solution of 1-dimensional Wave equation by Elzaki Transform. Internation Journal of Multidisciplinary Researcs and Development, 4(10), pp.64-67. |



 defined by:
defined by: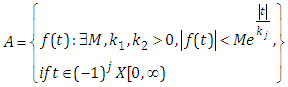
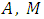 is constant must be finite,
is constant must be finite, 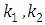 may be finite or infinite.The Elzaki transform is defined by
may be finite or infinite.The Elzaki transform is defined by 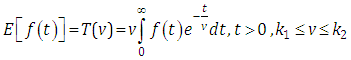
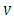 is used to factor the variable
is used to factor the variable 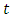 in the argument of function
in the argument of function 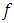 . This transform has deeper connection with the Laplace transform. The aim of this study is to show the applicability of this interesting new transform and its ability in solving the mixed order linear partial differential equations.
. This transform has deeper connection with the Laplace transform. The aim of this study is to show the applicability of this interesting new transform and its ability in solving the mixed order linear partial differential equations.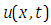 be a function of two independent variables
be a function of two independent variables 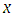 and
and 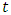 , then
, then 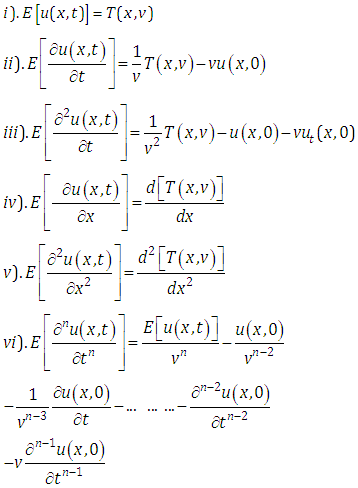
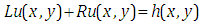
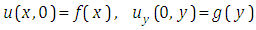
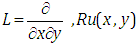 is the remaining linear terms in which contains only first order partial derivatives of
is the remaining linear terms in which contains only first order partial derivatives of 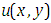 with respect to either
with respect to either  or
or 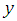 and
and 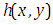 is the source term.We can write equation (3.1) in the following form
is the source term.We can write equation (3.1) in the following form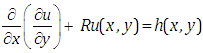
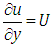 in equation (3.3), we obtain
in equation (3.3), we obtain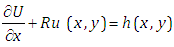
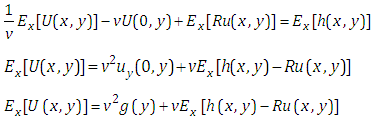
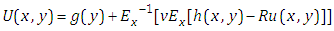
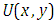 in equation (3.6), we get
in equation (3.6), we get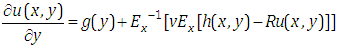
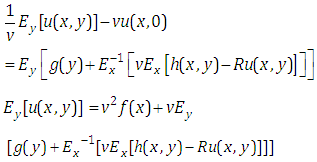
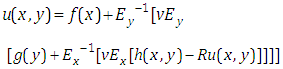
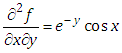
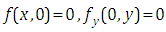
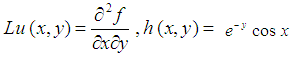 and general linear term
and general linear term 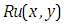 is zero.We can re-write equation (4.1) in the following form
is zero.We can re-write equation (4.1) in the following form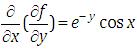
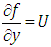 in equation (4.3), we get
in equation (4.3), we get 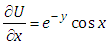
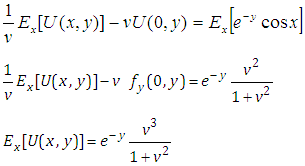
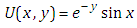
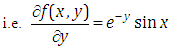
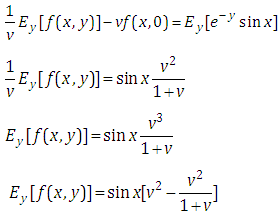
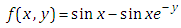
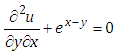
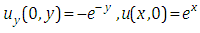
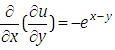
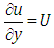 in equation (4.11), we get the non-homogeneous partial differential equation of first order is
in equation (4.11), we get the non-homogeneous partial differential equation of first order is 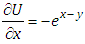
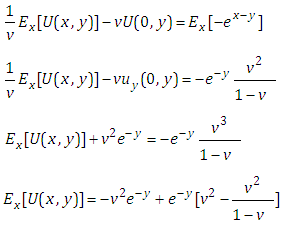
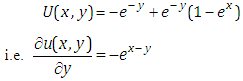
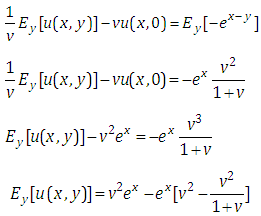
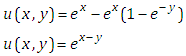 This is the required exact solution of equation (4.9). This can be verifying though the substitution.Example 3: Consider the linear partial differential equation
This is the required exact solution of equation (4.9). This can be verifying though the substitution.Example 3: Consider the linear partial differential equation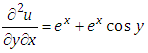
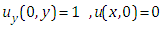
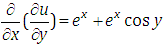
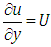 in equation (4.18), we get
in equation (4.18), we get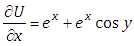
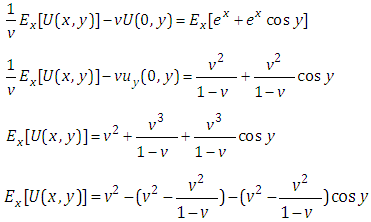
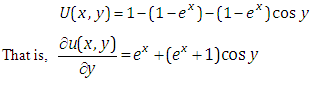
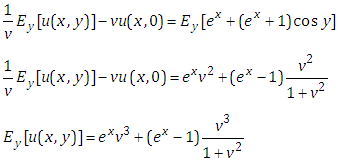
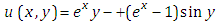 This is the required exact solution of equation (4.16). This can be verifying though the substitution.Example 4: Consider the linear partial differential equation with
This is the required exact solution of equation (4.16). This can be verifying though the substitution.Example 4: Consider the linear partial differential equation with 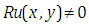
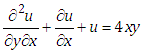
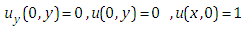
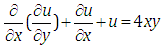
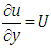 in equation (4.25), we get
in equation (4.25), we get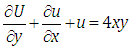
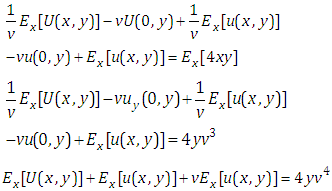
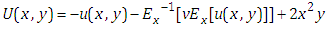 That is,
That is, 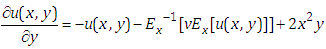
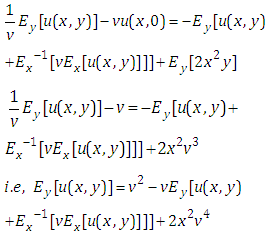
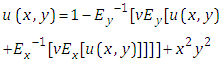 We cannot solve the equation (4.30) because our goal
We cannot solve the equation (4.30) because our goal 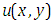 is appeared in both sides of equation (4.30). Thus the equation (4.23) we cannot solve by using Elzaki substitution method because of
is appeared in both sides of equation (4.30). Thus the equation (4.23) we cannot solve by using Elzaki substitution method because of 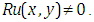
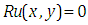 by proposed Elzaki Substitution Method. This result has been extracted that Elzaki Substitution Method plays a key role in finding the solution of higher order initial value problem which involves the mixed partial derivatives with general linear term
by proposed Elzaki Substitution Method. This result has been extracted that Elzaki Substitution Method plays a key role in finding the solution of higher order initial value problem which involves the mixed partial derivatives with general linear term 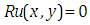 . The operation of this method is simple in use and time saving. But the result of example number four tell us that Elzaki Substitution Method is not applicable for those partial differential equations in which
. The operation of this method is simple in use and time saving. But the result of example number four tell us that Elzaki Substitution Method is not applicable for those partial differential equations in which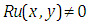 . Consequently the Elzaki Substitution Method can be applied for other equations that performing in various scientific fields.
. Consequently the Elzaki Substitution Method can be applied for other equations that performing in various scientific fields. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML