-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2018; 8(3): 47-49
doi:10.5923/j.ajcam.20180803.01

A New Method for Solving Nonlinear Equations Based on Euler’s Differential Equation
Masoud Saravi
Emeritus Professor of Islamic Azad University of Iran, Iran
Correspondence to: Masoud Saravi, Emeritus Professor of Islamic Azad University of Iran, Iran.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Usually the methods based on Taylor expansion series for 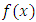 have better convergence [1]. But, nearly, all of them contain one or more derivatives of
have better convergence [1]. But, nearly, all of them contain one or more derivatives of 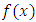 . The purpose of this paper is to introduce a technique to obtain free from derivatives which works better than methods others that been considered in most text book for solving nonlinear equations by providing some numerical examples.
. The purpose of this paper is to introduce a technique to obtain free from derivatives which works better than methods others that been considered in most text book for solving nonlinear equations by providing some numerical examples.
Keywords: Nonlinear equations, Order of convergence, Euler’s equation, Iteration formulae
Cite this paper: Masoud Saravi, A New Method for Solving Nonlinear Equations Based on Euler’s Differential Equation, American Journal of Computational and Applied Mathematics , Vol. 8 No. 3, 2018, pp. 47-49. doi: 10.5923/j.ajcam.20180803.01.
1. Introduction
- The problem of finding the roots of a given equation
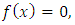 | (1) |
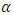 arise frequently in science and engineering. In most cases it is difficult to obtain an analytical solution of (1). Hence the exploitation of numerical methods for solving such equations becomes a main subject of considerable interests. Usually in all text books the methods split into two sections, namely methods without derivatives and methods with derivatives [2, 3, 4, 6, 8, 9, 10]. Probably the most well-known and widely used algorithm to find a root of
arise frequently in science and engineering. In most cases it is difficult to obtain an analytical solution of (1). Hence the exploitation of numerical methods for solving such equations becomes a main subject of considerable interests. Usually in all text books the methods split into two sections, namely methods without derivatives and methods with derivatives [2, 3, 4, 6, 8, 9, 10]. Probably the most well-known and widely used algorithm to find a root of 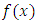 without derivative is the fixed point iteration method. In next section, we introduce a new algorithm and by expressing weak and strong aspect of this method, it will be deduced that the order of convergence is more than other methods without derivatives if the equation (1) contains simple roots.
without derivative is the fixed point iteration method. In next section, we introduce a new algorithm and by expressing weak and strong aspect of this method, it will be deduced that the order of convergence is more than other methods without derivatives if the equation (1) contains simple roots. 2. Procedure
- Expanding
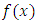 in (1) by Taylor's series about the point
in (1) by Taylor's series about the point 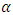 , we get
, we get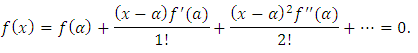 By approximating this series we may write
By approximating this series we may write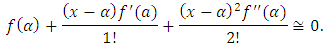 That is,
That is,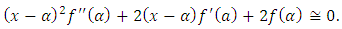 | (2) |
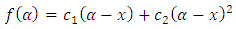 | (3) |
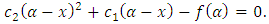 | (4) |
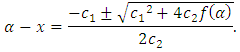 That is
That is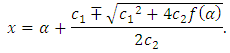 | (5) |
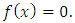
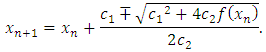 | (6) |
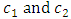 can be found by two choices for
can be found by two choices for 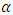 in (4). For example, let
in (4). For example, let 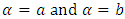 , then
, then 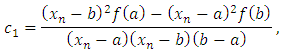 and
and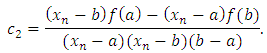 Therefore equation (6) becomes
Therefore equation (6) becomes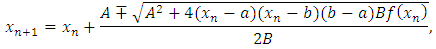 | (7) |
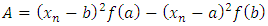 and
and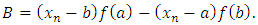 Remark 1: It should be noted that our starting value cannot be a or b, i.e.,
Remark 1: It should be noted that our starting value cannot be a or b, i.e., 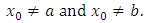 It would be better to start with
It would be better to start with 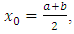 where
where 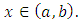 Remark 2: The sign,
Remark 2: The sign, 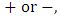 of the square root term is chosen to agree with the sign
of the square root term is chosen to agree with the sign 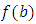 to keep
to keep 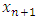 close to
close to 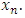 Remark 3: To find the order of convergence of this method we need some difficult square root computations, hence we avoid these computations. But the following examples in next section show that the order of convergence of this method must nearly be quadratic.
Remark 3: To find the order of convergence of this method we need some difficult square root computations, hence we avoid these computations. But the following examples in next section show that the order of convergence of this method must nearly be quadratic. 3. Numerical Examples
- This sections deals with some numerical test on some problems that been considered in several Numerical Analysis text books. We resolved them by this method and compare the results. Example 1: Consider
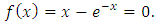 This equation has been taken from [5] and has a real root on (0,1). If we wish to approximate this root with accuracy 10-4 by the bisection method, we need 14 iterations to obtain an approximation accurate to 10-4. Because with
This equation has been taken from [5] and has a real root on (0,1). If we wish to approximate this root with accuracy 10-4 by the bisection method, we need 14 iterations to obtain an approximation accurate to 10-4. Because with 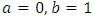 and
and 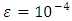 we get
we get 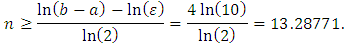 But if we apply our method, we obtain
But if we apply our method, we obtain 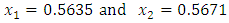 so that
so that 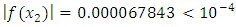 .Even we use chord (modified regula-falsi) method given by
.Even we use chord (modified regula-falsi) method given by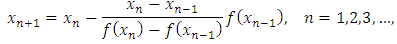 starting with
starting with 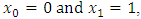 we come to following results:
we come to following results: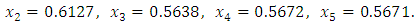 Example 2: Equation
Example 2: Equation 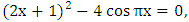 has a root in (1/4, 1/3). This equation been considered in [2]. The correct value to (4D) is
has a root in (1/4, 1/3). This equation been considered in [2]. The correct value to (4D) is 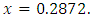 The authors used fixed point iteration formula showed that if we write
The authors used fixed point iteration formula showed that if we write 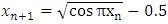 and start with mid-point of [1/4, 1/3] then
and start with mid-point of [1/4, 1/3] then 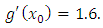 Since
Since 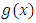 is continue there is an interval within [1/4, 1/3] over which
is continue there is an interval within [1/4, 1/3] over which 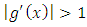 But by our method with plus sign (since f(1/3)>0) we obtained:
But by our method with plus sign (since f(1/3)>0) we obtained: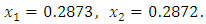 Although if they used a new scheme given by
Although if they used a new scheme given by 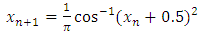 , with
, with 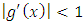 but with the same starting vale this scheme requires fifteen iterations to converges to the root 0.2872. Let's consider another example. This example was chosen from [3].Example 3: Approximate a zero of
but with the same starting vale this scheme requires fifteen iterations to converges to the root 0.2872. Let's consider another example. This example was chosen from [3].Example 3: Approximate a zero of 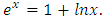 In this book only mentioned that this equation has not real root. The roots correct to (4d) are
In this book only mentioned that this equation has not real root. The roots correct to (4d) are 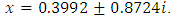 We used with starting value
We used with starting value 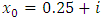 for fixed point iteration method and get
for fixed point iteration method and get 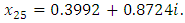 But by (7) we obtained
But by (7) we obtained 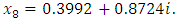 It seems this equation has only two conjugate complex roots, because we examined several numbers and every time we reached to this result. This fact may be examined by considering complex equation
It seems this equation has only two conjugate complex roots, because we examined several numbers and every time we reached to this result. This fact may be examined by considering complex equation 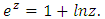 Example 4: Consider
Example 4: Consider 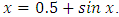 This equation has a root on (1, 2) and is given in [2,4, 5,6]. Let
This equation has a root on (1, 2) and is given in [2,4, 5,6]. Let 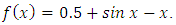 By fixed point iteration method we obtained following results:
By fixed point iteration method we obtained following results: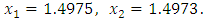 Of course in this example
Of course in this example 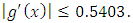 Now we apply our method. We have
Now we apply our method. We have 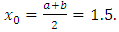 Since
Since 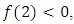 hence we use (7) with minus sign and we get
hence we use (7) with minus sign and we get 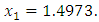 We also used Newton method with
We also used Newton method with 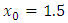 and get
and get 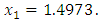 Note 1: Although by Newton method we had the same result on first iteration but this is not always true. See following example [4].Example 5: Consider
Note 1: Although by Newton method we had the same result on first iteration but this is not always true. See following example [4].Example 5: Consider 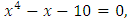 has a root in (1, 2). We used scheme given by (7) and get
has a root in (1, 2). We used scheme given by (7) and get 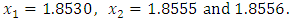 But by Newton’s method with
But by Newton’s method with 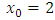 we obtained
we obtained 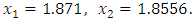 But with initial value
But with initial value 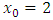 , in third iteration we get
, in third iteration we get 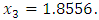 In general, the Newton method works better, in particular when the equation has complex roots. Let’s consider polynomial equations with all complex roots.Example 6: Approximate all roots of equation given by
In general, the Newton method works better, in particular when the equation has complex roots. Let’s consider polynomial equations with all complex roots.Example 6: Approximate all roots of equation given by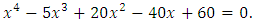 This example was chosen from [7]. In this book mentioned that this equation has not real roots and with starting value
This example was chosen from [7]. In this book mentioned that this equation has not real roots and with starting value 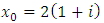 found
found 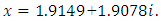 It is clear that a second root will be
It is clear that a second root will be 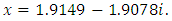 The other two roots are
The other two roots are 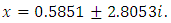 If we start with
If we start with 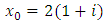 with
with 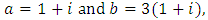 after 8 iterations we obtain
after 8 iterations we obtain 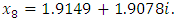 but by Newton method, with
but by Newton method, with 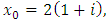 we need only two iterations.
we need only two iterations.4. Conclusions
- Results of all examples in this paper show the efficiency of this method comparing with other methods without derivatives. Although several methods free from derivatives been considered, but they contain too much computations [11, 12, 13, 14, 15, 16]. This method is not better than Newton method but it is not far from this method. In particular, sometimes its convergence is better than Newton method. If we compare with other methods which contain more differentiations is a useful formula to ignore differentiations. Author hope to extend this method to a system of nonlinear equations. Research in this matter is one of my future goals.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML