-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2018; 8(2): 37-45
doi:10.5923/j.ajcam.20180802.03

Analysis and Computation of Fuzzy Differential Equations via Interval Differential Equations with a Generalized Hukuhara-type Differentiability
J. Sunday
Department of Mathematics, Adamawa State University, Mubi, Nigeria
Correspondence to: J. Sunday, Department of Mathematics, Adamawa State University, Mubi, Nigeria.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

One of the most efficient ways to model the propagation of epistemic uncertainties (in dynamical environments/systems) encountered in applied sciences, engineering and even social sciences is to employ Fuzzy Differential Equations (FDEs). The FDEs are special type of Interval Differential Equations (IDEs). The IDEs are differential equations used to handle interval uncertainty that appears in many mathematical or computer models. The concept of generalized Hukuhara (gH) differentiability shall be applied in analyzing such equations. We further apply a highly efficient computational method to approximate the solution of some modeled FDEs. The results obtained clearly showed that the method adopted in the research is efficient and computationally reliable.
Keywords: Analysis, Computation, FDEs, Hukuhara differentiability, IDEs
Cite this paper: J. Sunday, Analysis and Computation of Fuzzy Differential Equations via Interval Differential Equations with a Generalized Hukuhara-type Differentiability, American Journal of Computational and Applied Mathematics , Vol. 8 No. 2, 2018, pp. 37-45. doi: 10.5923/j.ajcam.20180802.03.
Article Outline
1. Introduction
- It is no exaggeration to say that differential equations play important roles in modeling of physical and engineering problems, such as those in solid and fluid mechanics, viscoelasticity, biology, physics and many other areas, [1]. The theory of Fuzzy Differential Equations (FDEs) has focused much attention in the last decades since it provides good models for dynamical systems under uncertainty, [2].In general, the parameters, variables and initial conditions within a model are considered as being defined exactly. In reality, there may be only vague, imprecise or incomplete information about the variables and parameters available. This can result from errors in measurement, observation, or experimental data; or maintenance induced errors. To overcome uncertainties or lack of precision, one can use a fuzzy environment in parameters, variables and initial conditions in place of exact (fixed) ones by turning general differential equations into FDEs.In real applications, it can be complicated to obtain exact solution of FDEs due to the complexities in fuzzy arithmetic, creating the need for use of reliable and efficient numerical techniques in the solution of FDEs. Thus, there are many methods that have been derived to study FDEs. The first and most popular approach is using Hukuhara differentiability for fuzzy number value functions. Here, the existence and uniqueness of solutions of FDEs are analyzed. Under appropriate conditions, the FDEs that will be considered have locally two solutions. Some methods that exist in literature for the solutions of FDEs under the Hukuhara differentiability concept include Adomian decomposition method [3, 4], modified Euler’s method [5], Improved Runge-Kutta method [6], He’s homotopy perturbation method [7], Simpson’s rule [8], Picard method [9], Combined Laplace transformation and variational iteration methods [10], among others.Of recent, some results have been published on random FDEs. The random approach can be adequate in modeling of the dynamics of real phenomena which are subjected to two kinds of uncertainty: randomness and fuzziness simultaneously, [2]. Also, according to [5], the study of FDEs forms a suitable setting for mathematical modeling of real-world problems in which uncertainties or vagueness pervade.In this research, we shall be interested in the analysis and computation of FDEs of the form
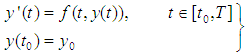 | (1) |
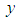 is a fuzzy function of
is a fuzzy function of 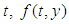 is a fuzzy function of the crisp variable
is a fuzzy function of the crisp variable 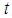 and the fuzzy variable
and the fuzzy variable 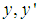 is the fuzzy derivative of
is the fuzzy derivative of 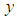 and
and 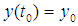 is a triangular or a triangular shaped fuzzy number.The sufficient conditions for the existence of a unique solution to the FDE (1) are that
is a triangular or a triangular shaped fuzzy number.The sufficient conditions for the existence of a unique solution to the FDE (1) are that 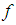 be continuous function satisfying the Lipschitz condition,
be continuous function satisfying the Lipschitz condition,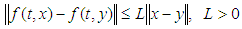 | (2) |
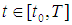 by a set of discrete equally spaced grid points
by a set of discrete equally spaced grid points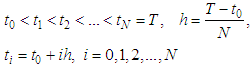
2. Preliminaries
- In this section, some definitions shall be presented. We shall also introduce some necessary notations that shall be employed in this paper.Consider the space
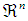 of
of 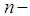 dimensional real numbers and let
dimensional real numbers and let 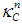 be the space of nonempty compact and convex sets of
be the space of nonempty compact and convex sets of 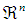 . If
. If 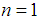 , denote
, denote 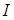 the set of (closed bounded) intervals of the real line. Let
the set of (closed bounded) intervals of the real line. Let 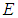 be the set of all upper semi-continuous normal convex fuzzy numbers with bounded
be the set of all upper semi-continuous normal convex fuzzy numbers with bounded 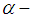 level intervals. Then,
level intervals. Then, 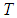 is the set of all triangular or triangular shaped fuzzy number and
is the set of all triangular or triangular shaped fuzzy number and 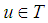 .Definition [11]A fuzzy number is a fuzzy subset of the real line with normal, convex and upper semi continuous membership function of bounded support. A fuzzy number
.Definition [11]A fuzzy number is a fuzzy subset of the real line with normal, convex and upper semi continuous membership function of bounded support. A fuzzy number 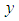 is represented by an ordered pair of functions
is represented by an ordered pair of functions 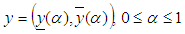 which satisfies the following three conditions:(i)
which satisfies the following three conditions:(i) 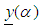 is a bounded left continuous non-decreasing function
is a bounded left continuous non-decreasing function 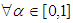 (ii)
(ii) 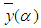 is a bounded right continuous non-increasing function
is a bounded right continuous non-increasing function 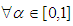 (iii)
(iii) 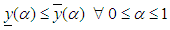 A fuzzy number is a generalization of a regular, real number in the sense that it does not refer to one single value but rather to a connected set of possible values, where each possible value has its own weight between 0 and 1. This weight is called the membership function.It is important to state that our fuzzy number will be triangular shaped. A triangular fuzzy number
A fuzzy number is a generalization of a regular, real number in the sense that it does not refer to one single value but rather to a connected set of possible values, where each possible value has its own weight between 0 and 1. This weight is called the membership function.It is important to state that our fuzzy number will be triangular shaped. A triangular fuzzy number 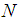 is defined by three real numbers
is defined by three real numbers 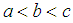 , where the base of the triangle is the interval
, where the base of the triangle is the interval 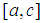 and its vertex is at
and its vertex is at 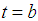 .Triangular fuzzy numbers will be written as
.Triangular fuzzy numbers will be written as 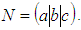 The membership function for the triangular fuzzy number
The membership function for the triangular fuzzy number 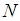 is defined as
is defined as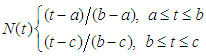 | (3) |
 (ii) momotonically decreasing on
(ii) momotonically decreasing on  also, the core of a fuzzy number is the set of values where the membership value equals one, [12].Definition [5]Let
also, the core of a fuzzy number is the set of values where the membership value equals one, [12].Definition [5]Let  be a nonempty set. A fuzzy set
be a nonempty set. A fuzzy set 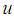 in
in 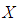 is characterized by its membership function
is characterized by its membership function 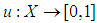 . Then
. Then 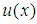 is interpreted as the degree of membership of an element
is interpreted as the degree of membership of an element 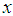 in the fuzzy set
in the fuzzy set 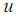 for each
for each 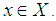 Definition [13]The generalized Hukuhara difference of two sets
Definition [13]The generalized Hukuhara difference of two sets 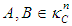 (
(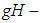 difference for short) is defined as follows,
difference for short) is defined as follows,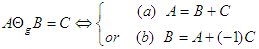 | (4) |
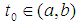 and
and 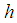 be such that
be such that 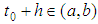 , then the gH-derivative of a function
, then the gH-derivative of a function 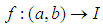 can be defined as
can be defined as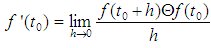 | (5) |
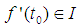 satisfying (5) exists, we say that
satisfying (5) exists, we say that 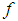 is generalized Hukuhara differentiable (
is generalized Hukuhara differentiable (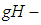 differentiable for short) at
differentiable for short) at 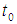 . It is important to state that sometimes,
. It is important to state that sometimes, 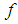 may be strongly generalized (Hukuhara) or weakly generalized (Hukuhara) differentiable at
may be strongly generalized (Hukuhara) or weakly generalized (Hukuhara) differentiable at 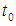 .We denote the fuzzy function
.We denote the fuzzy function 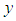 by
by 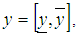 where
where 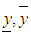 are lower and upper branches of
are lower and upper branches of 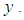 Definition [14]Let
Definition [14]Let 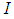 be a real interval. A mapping
be a real interval. A mapping 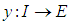 is called a fuzzy process and we define its
is called a fuzzy process and we define its  level set as
level set as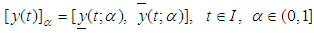 | (6) |
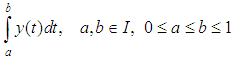 is defined by
is defined by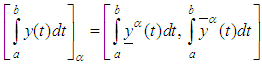 | (7) |
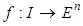 is Hukuhara differentiable and its Hukuhara derivative
is Hukuhara differentiable and its Hukuhara derivative 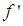 is integrable over
is integrable over 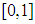 then,
then,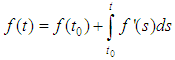 | (8) |
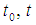 where
where 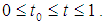 Definition [15]A numerical integration scheme is said to be
Definition [15]A numerical integration scheme is said to be 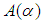 -stable for some
-stable for some 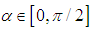 if the wedge
if the wedge 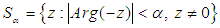 | (9) |
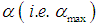 is called the angle of absolute stability.
is called the angle of absolute stability.3. Interval Differential Equations and the Generalized Hukuhara Differentiability
- According to [13], generalization of the concept of Hukuhara differentiability can be of great help in the study of IDEs. Consider the IDE
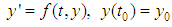 | (10) |
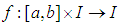 with,
with, 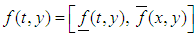 for
for 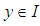
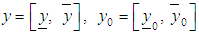 Lemma 3.1 [13]The IDE (10) is locally equivalent to the integral equation
Lemma 3.1 [13]The IDE (10) is locally equivalent to the integral equation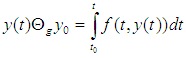 | (11) |
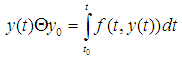 and
and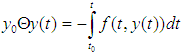 with
with 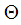 being the classical Hukuhara difference.This integral equation formulation helps us in obtaining existence result for IDEs.Theorem 3.1 [13]Let
being the classical Hukuhara difference.This integral equation formulation helps us in obtaining existence result for IDEs.Theorem 3.1 [13]Let 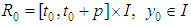 nontrivial and
nontrivial and 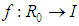 be continuous. If
be continuous. If 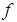 satisfies the Lipchitz condition
satisfies the Lipchitz condition 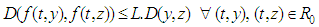 , then the interval problem (10) and by extension the FDE (1) has exactly two solutions
, then the interval problem (10) and by extension the FDE (1) has exactly two solutions 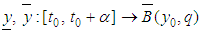 satisfying
satisfying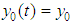
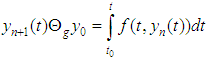 More precisely, the successive iterations
More precisely, the successive iterations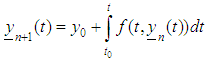 and
and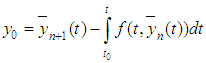 converge to these two solutions
converge to these two solutions 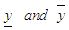 respectively.See [13] for proof.
respectively.See [13] for proof.4. Derivation of a Computational Method and Analysis of Its Basic Properties
- In order to compute the approximate solution to FDEs of the form (1), we derive a highly efficient two-step computational method that has the form,
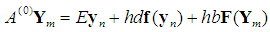 | (12) |
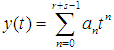 | (13) |
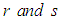 are the numbers of collocation and interpolation points respectively. Let the approximate solution to FDE (1) be given by power series of degree 5; taking
are the numbers of collocation and interpolation points respectively. Let the approximate solution to FDE (1) be given by power series of degree 5; taking 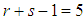 in equation (13) gives,
in equation (13) gives,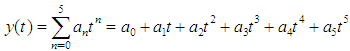 | (14) |
 | (15) |
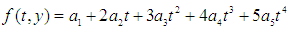 | (16) |
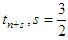 and collocating (16) at points
and collocating (16) at points 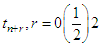 , leads to a system of nonlinear equation of the form,
, leads to a system of nonlinear equation of the form,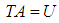 | (17) |
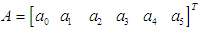
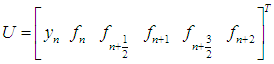
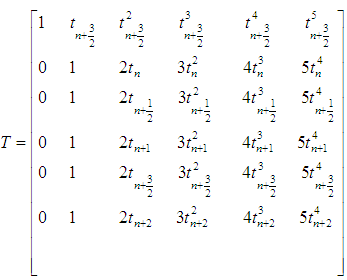 Solving the system (17) by Gauss elimination method for the
Solving the system (17) by Gauss elimination method for the 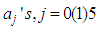 and substituting back into the power series basis function gives a linear multistep method of the form,
and substituting back into the power series basis function gives a linear multistep method of the form,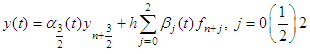 | (18) |
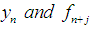 are given by,
are given by,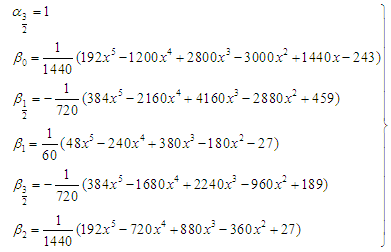 | (19) |
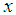 is given as
is given as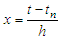 | (20) |
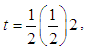 gives a discrete two-step computational method of the (12) given by,
gives a discrete two-step computational method of the (12) given by, | (21) |
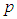 of the computational method and error constants are given respectively by
of the computational method and error constants are given respectively by 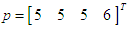 and
and 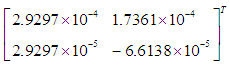 (ii) The method is adjudged to be consistent since it has order
(ii) The method is adjudged to be consistent since it has order  . Note that consistency controls the magnitude of the local truncation error committed at each stage of the computation, [16](iii) The computational method is said to be zero-stable, if the roots
. Note that consistency controls the magnitude of the local truncation error committed at each stage of the computation, [16](iii) The computational method is said to be zero-stable, if the roots  of the first characteristic polynomial
of the first characteristic polynomial 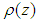 defined by
defined by 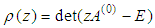 satisfies
satisfies 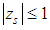 and every root satisfying
and every root satisfying 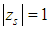 have multiplicity not exceeding the order of the differential equation, [16, 17]. The first characteristic polynomial is given by,
have multiplicity not exceeding the order of the differential equation, [16, 17]. The first characteristic polynomial is given by, 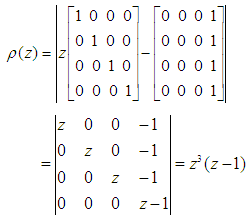 Thus, solving for in
Thus, solving for in 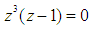 | (22) |
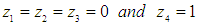 . Hence, the computational method (21) is said to be zero-stable.(iv) The computational method is convergent since it is consistent and zero-stable.(v) The region of absolute stability of the computational method is shown in the figure below
. Hence, the computational method (21) is said to be zero-stable.(iv) The computational method is convergent since it is consistent and zero-stable.(v) The region of absolute stability of the computational method is shown in the figure below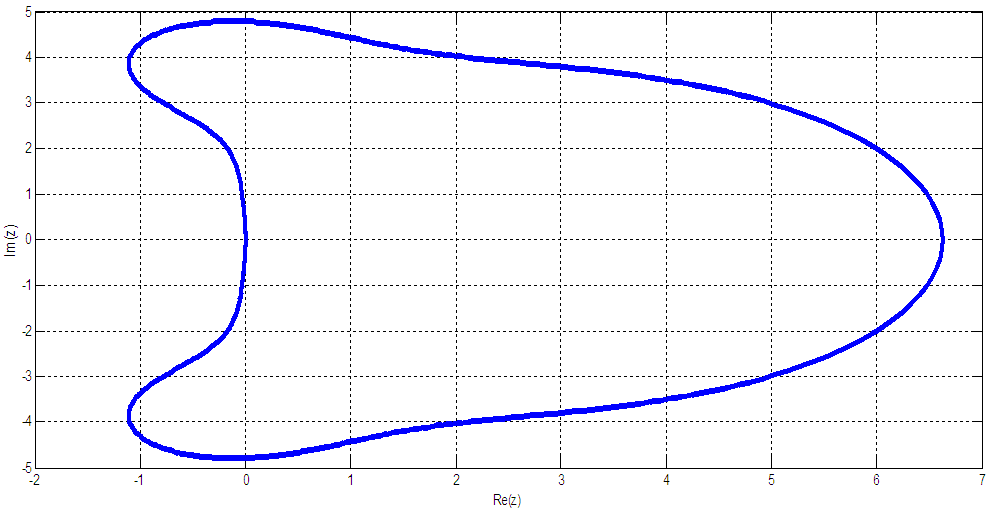 | Figure 4.1. Stability region of the computational method |
 -stable, since the stability region consists of the complex plane outside the enclosed figure. Note that the unstable region is the interior of the curve (when the curve is on the positive plane) while the stability region contains the exterior part of the curve.
-stable, since the stability region consists of the complex plane outside the enclosed figure. Note that the unstable region is the interior of the curve (when the curve is on the positive plane) while the stability region contains the exterior part of the curve.5. Results
- Let
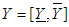 and
and 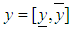 denote respectively the exact (analytic) solution and approximate (computed) solution of the fuzzy differential equations of the form (1). That is,
denote respectively the exact (analytic) solution and approximate (computed) solution of the fuzzy differential equations of the form (1). That is,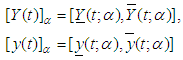 Also, let absolute error
Also, let absolute error 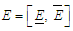 be defined by
be defined by 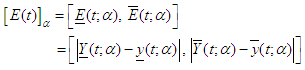 We shall apply the computational method derived on some FDEs to test its efficiency and reliability. It is important to state that the FDEs that shall be solved in this section are all interval differential equations.Problem 5.1: Consider the Fuzzy differential equation,
We shall apply the computational method derived on some FDEs to test its efficiency and reliability. It is important to state that the FDEs that shall be solved in this section are all interval differential equations.Problem 5.1: Consider the Fuzzy differential equation, 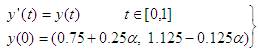 | (23) |
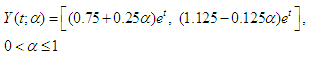 | (24) |
 Source: [18]
Source: [18]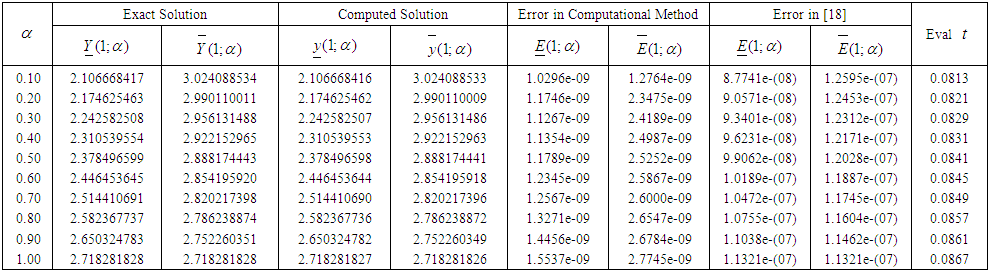 | Table 5.1. Showing the result for Problem 5.1 at t = 1 |
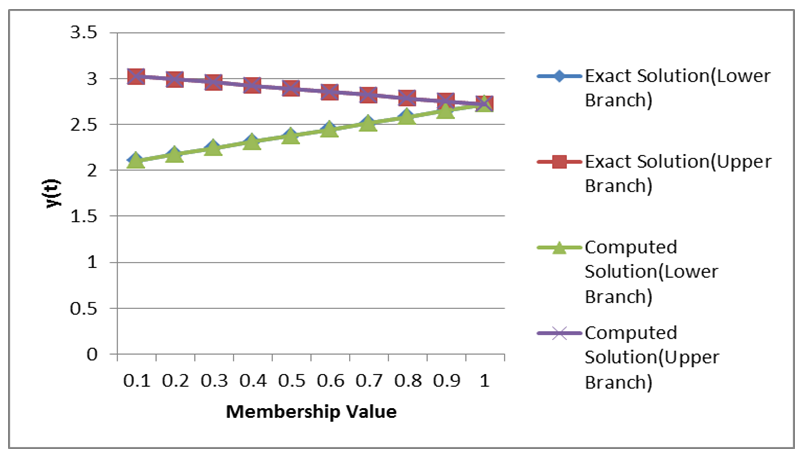 | Figure 5.1. Graphical results comparing the exact and computed solutions for Problem 5.1 |
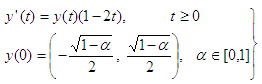 | (25) |
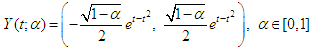 | (26) |
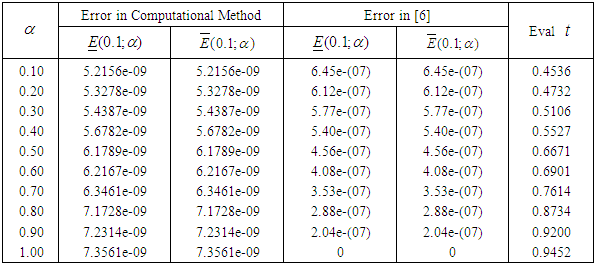
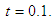 Source: [6]
Source: [6]
|
 | Figure 5.2. Graphical results comparing the absolute errors in the computational method with that of [6] for Problem 5.2 |
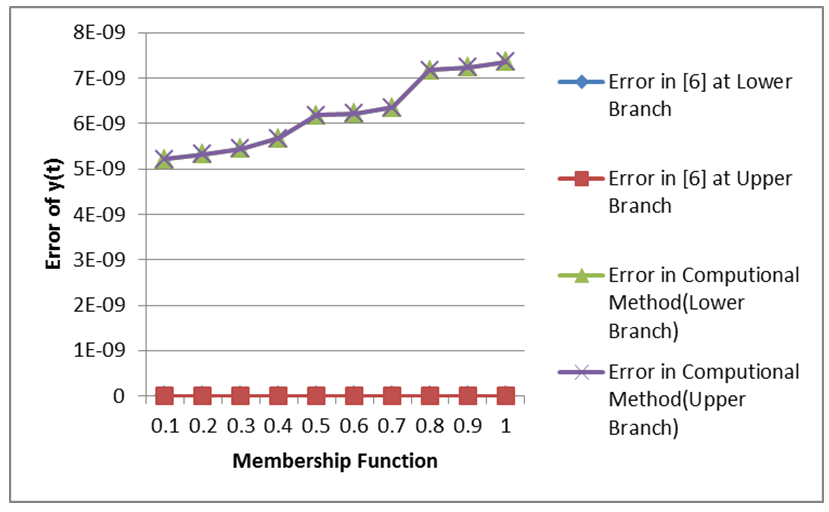
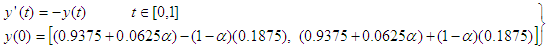 | (27) |
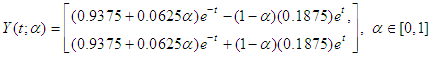 | (28) |
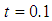 Source: [18]
Source: [18]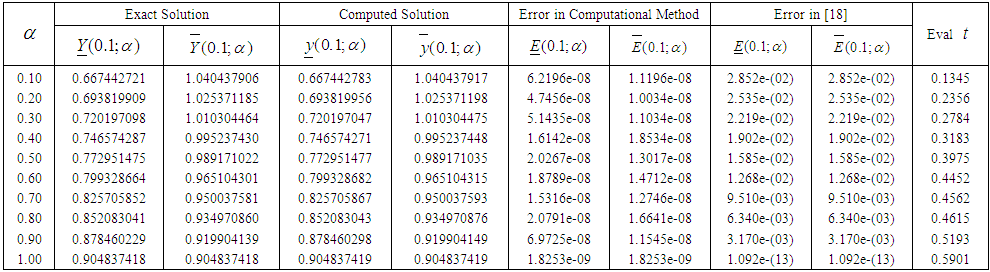 | Table 5.3. Showing the result for Problem 5.3 at t = 0.1 |
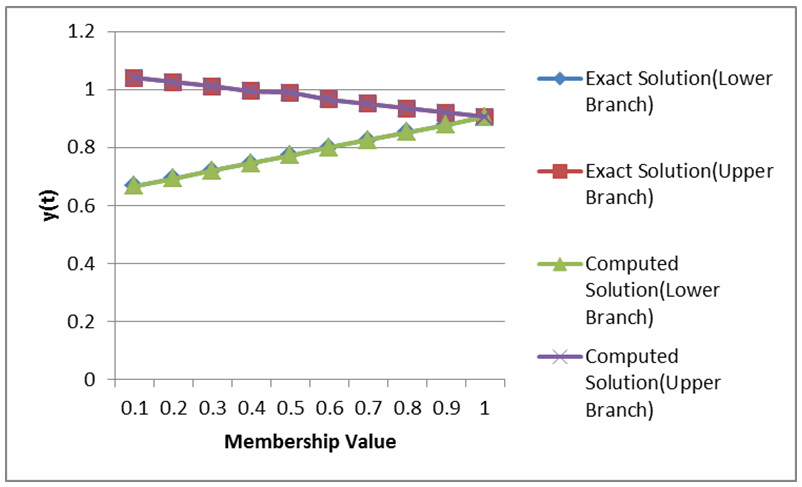 | Figure 5.3. Graphical results comparing the exact and computed solutions for Problem 5.3 |
6. Conclusions
- IDEs with a generalized Hukuhara type differentiability were studied to obtain an existence theorem and uniqueness of two solutions for FDEs. Special case interval differential equations called the fuzzy differential equations have been studied. We also looked at the influence of Hukuhara differentiability on such differential equations. It is however important to state that the setback of this approach is that the solution becomes fuzzier as time goes by. Thus, the fuzzy solution behaves quite differently from the crisp solution. To avoid this setback, [19] interpreted FDEs as a family of differential inclusions. However, the main shortcoming of using differential inclusions is that we do not have a derivative of a fuzzy-number-valued function, [5].In view of these shortcomings, the generalized differentiability was introduced in [20, 21, 22] where the original initial value problem is replaced by two parametric ordinary differential systems which are then solved numerically using classical algorithm. You may refer to the work of [23], where they applied the block backward differentiation formula under generalized differentiability.Conclusively, one may also say that the computational method adopted in this research effectively approximates the FDEs.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML