R. Thukral
Padé Research Centre, England
Correspondence to: R. Thukral, Padé Research Centre, England.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
A new secant-type method for finding zeros of nonlinear equations is presented. In terms of computational cost the new iterative method requires two evaluations of functions per iteration. It is shown and proved that the new method has a convergence of order 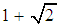 . We examine the effectiveness of the new method by approximating the simple root of several nonlinear equations. Numerical examples are given to demonstrate exceptional convergence speed of the proposed method. It is observed that our proposed method is competitive with other similar robust methods and very effective in high precision computations.
. We examine the effectiveness of the new method by approximating the simple root of several nonlinear equations. Numerical examples are given to demonstrate exceptional convergence speed of the proposed method. It is observed that our proposed method is competitive with other similar robust methods and very effective in high precision computations.
Keywords:
Secant method, Newton method, Simple root, Nonlinear equations, Root-finding, Order of convergence
Cite this paper: R. Thukral, A New Secant-type Method for Solving Nonlinear Equations, American Journal of Computational and Applied Mathematics , Vol. 8 No. 2, 2018, pp. 32-36. doi: 10.5923/j.ajcam.20180802.02.
1. Introduction
Finding the root of nonlinear equations is one of important problem in science and engineering [5]. In this paper, we present a new iterative method to find a simple root  of the nonlinear equation
of the nonlinear equation 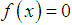 , where
, where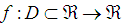 for an open interval D is a scalar function. The multipoint root-solvers is of great practical importance since it overcomes theoretical limits of one-point methods concerning the convergence order and computational efficiency. In recent years, some modifications of the Newton-type methods for simple root have been proposed and analysed [5] and very little work has been done on the secant-type methods. Therefore, the purpose of this paper is to show further development of the secant-type methods. In addition, we will demonstrate the similarity between the Fernandez-Torres and Tiruneh et al. method. We have found that the efficiency index of new iterative method has a better efficiency index than the classical Newton method and equivalent to the Fernandez-Torres, Tiruneh et al. and McDougall et al. methods [1, 3, 6]. Furthermore, we demonstrate the performance of the new method is significantly better when compared with the established methods.The two well-known iterative methods for finding simple root of nonlinear equations are namely, the classical secant method and the classical Newton method, given by
for an open interval D is a scalar function. The multipoint root-solvers is of great practical importance since it overcomes theoretical limits of one-point methods concerning the convergence order and computational efficiency. In recent years, some modifications of the Newton-type methods for simple root have been proposed and analysed [5] and very little work has been done on the secant-type methods. Therefore, the purpose of this paper is to show further development of the secant-type methods. In addition, we will demonstrate the similarity between the Fernandez-Torres and Tiruneh et al. method. We have found that the efficiency index of new iterative method has a better efficiency index than the classical Newton method and equivalent to the Fernandez-Torres, Tiruneh et al. and McDougall et al. methods [1, 3, 6]. Furthermore, we demonstrate the performance of the new method is significantly better when compared with the established methods.The two well-known iterative methods for finding simple root of nonlinear equations are namely, the classical secant method and the classical Newton method, given by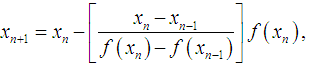 | (1) |
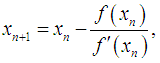 | (2) |
and their order of convergence is 1.618 and 2 respectively. For the purpose of this paper, we present a new secant-type method for finding simple root of nonlinear equations.The structure of this paper is as follows: Some basic definitions relevant to the present work are presented in the section 2. In section 3 the new secant-type method and prove the order of convergence are described. In section 4 we demonstrate the equivalency of the two methods recently introduced. Finally, in section 5, numerical comparisons are made to demonstrate the performance of the presented method.
2. Review of Definitions
In order to establish the order of convergence of an iterative method, following definitions are used [1].Definition 1 Let 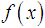 be a real-valued function with a root
be a real-valued function with a root 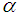 and let
and let 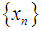 be a sequence of real numbers that converge towards
be a sequence of real numbers that converge towards 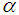 . The order of convergence p is given by
. The order of convergence p is given by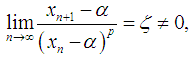 | (3) |
where 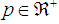 and
and 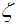 is the asymptotic error constant [2, 5, 7].Definition 2 Let
is the asymptotic error constant [2, 5, 7].Definition 2 Let 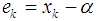 be the error in the kth iteration, then the relation
be the error in the kth iteration, then the relation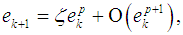 | (4) |
is the error equation. If the error equation exists, then p is the order of convergence of the iterative method [2, 5, 7].Definition 3 Let r be the number of function evaluations of the method. The efficiency of the method is measured by the concept of efficiency index and defined as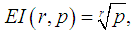 | (5) |
where p is the order of convergence of the method [4].Definition 4 Suppose that 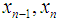 and
and 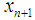 are three successive iterations closer to the root
are three successive iterations closer to the root 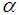 of (1). Then the computational order of convergence may be approximated by
of (1). Then the computational order of convergence may be approximated by 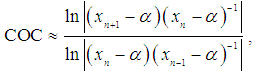 | (6) |
further details may be found in [8].
3. The Method and Analysis of Convergence
In this section, we shall define the new iterative method, namely, the secant-type method. To obtain the solution of (1), the new method requires two evaluations of functions and set a particular initial point, ideally close to the simple root. Therefore the expression of the new iterative method for determining the simple root of (1) is given as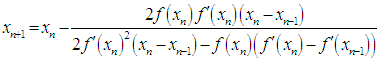 | (7) |
where 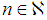 ,
, 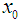 is the initial value and provided that the denominator of (7) is not equal to zero. It is essential to verify our finding and prove the order of convergence of the new iterative method.TheoremAssume that the function
is the initial value and provided that the denominator of (7) is not equal to zero. It is essential to verify our finding and prove the order of convergence of the new iterative method.TheoremAssume that the function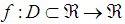 for an open interval D has a simple root
for an open interval D has a simple root 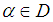 . Let
. Let 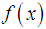 be sufficiently smooth in the interval D. If the initial points
be sufficiently smooth in the interval D. If the initial points 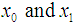 are sufficiently close to
are sufficiently close to 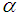 , then the asymptotic convergence order of the new method defined by (7) is
, then the asymptotic convergence order of the new method defined by (7) is 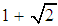 . Proof Let
. Proof Let 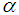 be a simple root of
be a simple root of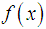 , i.e.
, i.e. 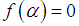 and
and 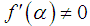 , and the errors at
, and the errors at 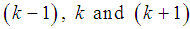 iteration are expressed as
iteration are expressed as 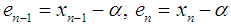 and
and 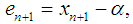 respectively.Using Taylor expansion and taking into account that
respectively.Using Taylor expansion and taking into account that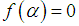 , we have
, we have 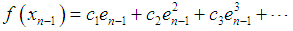 | (8) |
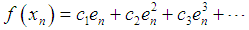 | (9) |
where 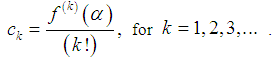 | (10) |
Furthermore, we have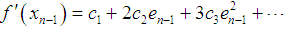 | (11) |
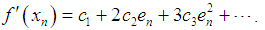 | (12) |
By substituting the above expressions in the numerator of (7), we obtain 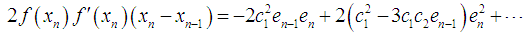 | (13) |
and similarly the denominator of (7) is given as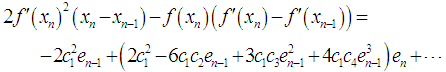 | (14) |
Dividing (14) by (13) and simplifying, we have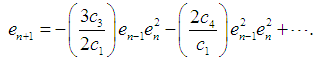 | (15) |
In order to prove the order of convergence of (15), we define positive real terms of 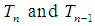 as
as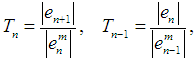 | (16) |
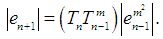 | (17) |
Therefore, from (15) we obtain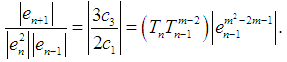 | (18) |
In order to satisfy the asymptotic equation (18), the power of the error term shall approach zero, that is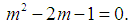 | (19) |
It is obvious that quadratic equation (19) has two roots,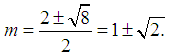 | (20) |
The order of convergence of the method (7) is determined by the positive root of (20). Hence, the new method defined by (7) has a convergence order of 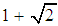 . This completes the proof. The new method (7) requires 2 function evaluations and has the order of convergence
. This completes the proof. The new method (7) requires 2 function evaluations and has the order of convergence 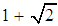 and to determine the efficiency index of the new method, definition 3 shall be used. Hence, the efficiency index of the new iterative method given by (7) is
and to determine the efficiency index of the new method, definition 3 shall be used. Hence, the efficiency index of the new iterative method given by (7) is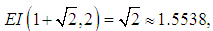 | (21) |
and the efficiency index of the Newton method and the secant method is given by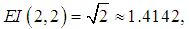 | (22) |
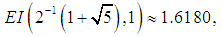 | (23) |
respectively. This indicates that the new method has a better efficiency index than the Newton method and is equivalent to the Fernandez-Torres, Tiruneh et al. and McDougall et al. methods.
4. The Established Methods
For the purpose of comparison, three well-known iterative methods are considered namely, the McDougall et al., the Fernandez-Torres method and the Tiruneh et al. methods. Since these methods are well established, the essential formulas are used to calculate the approximate solution of the given nonlinear equations and thus compare the effectiveness of the new method. First we will state the Fernandez-Torres method and the Tiruneh et al. method and then demonstrate the similarity between these methods.In [1], Fernandez-Torres developed a super-quadratic convergence order method for finding simple root of nonlinear equations, the essential expression used in the method is given as,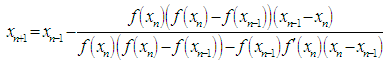 | (24) |
The Tiruneh et al. method given in [7] is also a super-quadratic convergence order method for finding simple root of nonlinear equations and is expressed as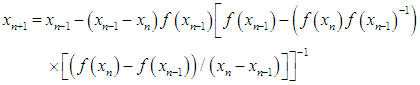 | (25) |
To demonstrate the equivalency of these methods we will first denote the following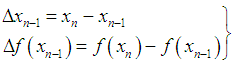 | (26) |
Using (26) and simplifying the Fernandez-Torres method (24), we get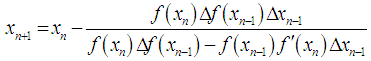 | (27) |
and similarly Tiruneh et al. method (25) is given as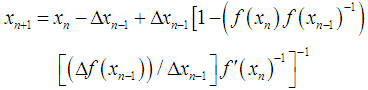 | (28) |
To demonstrate the Fernandez-Torres and Tiruneh et al. methods produce identical approximation of the simple root of the nonlinear equation, hence, we simply equate the two methods.Let 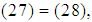 we have
we have 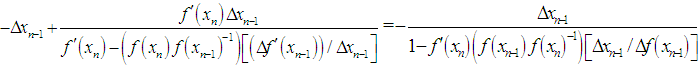 | (29) |
Cancelling common factors, we obtain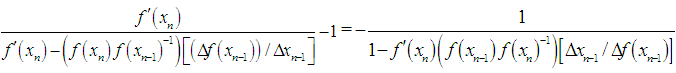 | (30) |
Simplifying, we get 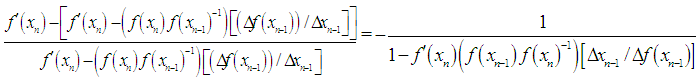 | (31) |
Further simplification yields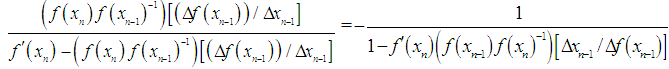 | (32) |
Applying cross-multiplication rule to (32), we obtain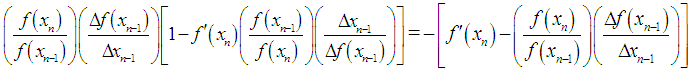 | (33) |
Expanding (33), we have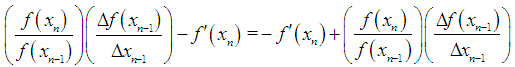 | (34) |
The equation (34) establishes that the Fernandez-Torres and Tiruneh et al. methods produce identical estimates of the simple root of the nonlinear equation. Furthermore, this is manifested in the numerical examples.Another super-quadratic convergence order method for finding simple root of nonlinear equations was presented by McDougall et al. [3], we state the essential expressions used in the method. The initial points are given as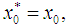 | (35) |
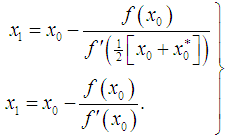 | (36) |
Then the calculation of the simple root of the nonlinear equation is given by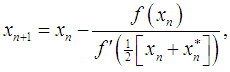 | (37) |
where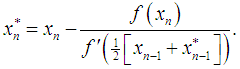 | (38) |
5. Numerical Examples
The proposed iterative method given by (7) is employed to solve nonlinear equation with simple root. The difference between the simple root 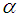 and the approximation
and the approximation 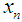 for test function with initial guess
for test function with initial guess 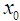 is displayed in tables. Furthermore, the computational order of convergence approximations are displayed in tables and we observe that this perfectly coincides with the theoretical result. The numerical computations listed in the table was performed on an algebraic system called Maple and the errors displayed are of absolute value. The results in the tables were obtained by the following algorithm Algorithm (Maple program) sroots:=[fsolve(f(x),x)]:root1:=sroots[1];diff(f(x),x);x[0]:=x0:dfx[0]:= diff(f(x),x);x[1]:=x[0]-fx[0]/dfx[0]:for n from 1 to 6 dofx[n]:=f(x);dfx[n]:=diff(f(x),x);x1[n]:=x[n]-x[n-1]:dfxx[n]:=dfx[n]-dfx[n-1]:x[n+1]:=evalf(x[n]-(2fx[n]dfx[n]x1[n])/(2dfx[n]^2x1[n]- fx[n]dfxx[n]);new[n]:=root1-x[n];coc:=evalf(ln(new[n]/new[n-1])/(ln(new[n-1]/new[n-2]));print(n,new[n],coc);end:Numerical example 1We will demonstrate the convergence of the new iterative method for the following nonlinear equation
is displayed in tables. Furthermore, the computational order of convergence approximations are displayed in tables and we observe that this perfectly coincides with the theoretical result. The numerical computations listed in the table was performed on an algebraic system called Maple and the errors displayed are of absolute value. The results in the tables were obtained by the following algorithm Algorithm (Maple program) sroots:=[fsolve(f(x),x)]:root1:=sroots[1];diff(f(x),x);x[0]:=x0:dfx[0]:= diff(f(x),x);x[1]:=x[0]-fx[0]/dfx[0]:for n from 1 to 6 dofx[n]:=f(x);dfx[n]:=diff(f(x),x);x1[n]:=x[n]-x[n-1]:dfxx[n]:=dfx[n]-dfx[n-1]:x[n+1]:=evalf(x[n]-(2fx[n]dfx[n]x1[n])/(2dfx[n]^2x1[n]- fx[n]dfxx[n]);new[n]:=root1-x[n];coc:=evalf(ln(new[n]/new[n-1])/(ln(new[n-1]/new[n-2]));print(n,new[n],coc);end:Numerical example 1We will demonstrate the convergence of the new iterative method for the following nonlinear equation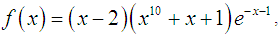 | (39) |
Having the exact value of the simple root of (39) is 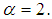 In Table 1 are the errors obtained by the methods described, based on the initial point (IP)
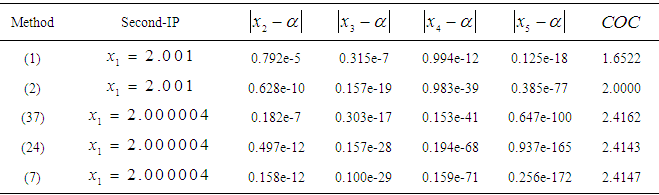
In Table 1 are the errors obtained by the methods described, based on the initial point (IP) 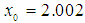 . We observe that the new iterative method is converging to the expected order.
. We observe that the new iterative method is converging to the expected order. Table 1. Errors occurring in the estimates of the simple root of (39) by the methods described
 |
| |
|
Numerical example 2We will demonstrate the convergence of the new iterative method for the following nonlinear equation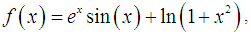 | (40) |
Having the exact value of the simple root of (40) is 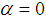 In Table 2 are the errors obtained by the methods described, based on the initial value
In Table 2 are the errors obtained by the methods described, based on the initial value 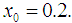
Table 2. Errors occurring in the estimates of the simple root of (40) by the methods described
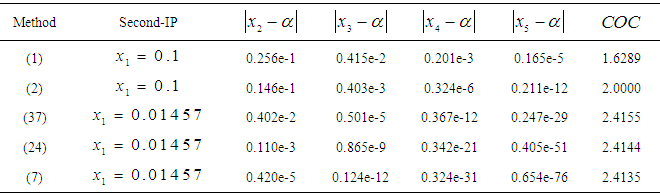 |
| |
|
Numerical example 3We will demonstrate the convergence of the new method for the following nonlinear equation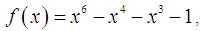 | (41) |
having the exact value of the simple root of (41) is 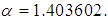 In Table 3 are the errors obtained by the methods described, based on the initial value
In Table 3 are the errors obtained by the methods described, based on the initial value 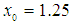 .
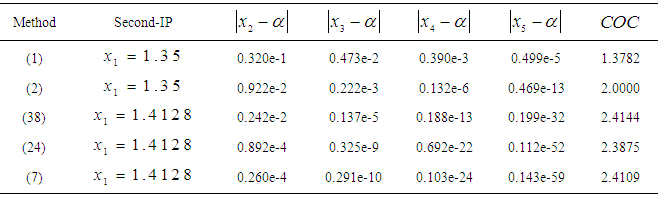
.Table 3. Errors occurring in the estimates of the simple root of (41) by the methods described
 |
| |
|
6. Conclusions
A new secant-type method for solving nonlinear equations with simple root has been presented. The effectiveness of the new method is examined by showing the accuracy of the simple root of several nonlinear equations. We have shown numerically and verified that the new iterative method has convergence of order 2.414. The major advantage of the new method is that it is very effective and produces high precision of approximation of the simple root. Finally, we conclude that the new method may be considered a very good alternative to the classical methods.
References
| [1] | G. Fernandez-Torres, A novel geometric modification of the Newton-secant method to achieve convergence of order 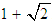 . and its dynamics, Mod. Sim. Eng. 2015 art. ID 502854. . and its dynamics, Mod. Sim. Eng. 2015 art. ID 502854. |
| [2] | W. Gautschi, Numerical Analysis: an Introduction, Birkhauser, 1997. |
| [3] | T. J. McDougall, S. J. Wotherspoon, A simple modification of Newton’s method to achieve convergence of order 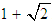 . Appl. Math. Lett. 29 (2014) 20-25. . Appl. Math. Lett. 29 (2014) 20-25. |
| [4] | A. M. Ostrowski, Solutions of equations and system of equations, Academic Press, New York, 1960. |
| [5] | M. S. Petkovic, B. Neta, L. D. Petkovic, J. Dzunic, Multipoint methods for solving nonlinear equations, Elsevier 2012. |
| [6] | A.T. Tiruneh, W. N. Ndlela, S. J. Nkambule, A two-point Newton method suitable for non-convergent cases and with super-quadratic convergence, Adv. Numer. Anal. 2013 art. ID 687382. |
| [7] | J. F. Traub, Iterative Methods for solution of equations, Chelsea publishing company, New York 1977. |
| [8] | S. Weerakoon, T. G. I. Fernando, A variant of Newton’s method with accelerated thirdorder convergence Appl. Math. Lett. 13 (2000) 87-93. |


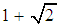 . We examine the effectiveness of the new method by approximating the simple root of several nonlinear equations. Numerical examples are given to demonstrate exceptional convergence speed of the proposed method. It is observed that our proposed method is competitive with other similar robust methods and very effective in high precision computations.
. We examine the effectiveness of the new method by approximating the simple root of several nonlinear equations. Numerical examples are given to demonstrate exceptional convergence speed of the proposed method. It is observed that our proposed method is competitive with other similar robust methods and very effective in high precision computations.
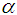 of the nonlinear equation
of the nonlinear equation 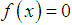 , where
, where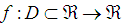 for an open interval D is a scalar function. The multipoint root-solvers is of great practical importance since it overcomes theoretical limits of one-point methods concerning the convergence order and computational efficiency. In recent years, some modifications of the Newton-type methods for simple root have been proposed and analysed [5] and very little work has been done on the secant-type methods. Therefore, the purpose of this paper is to show further development of the secant-type methods. In addition, we will demonstrate the similarity between the Fernandez-Torres and Tiruneh et al. method. We have found that the efficiency index of new iterative method has a better efficiency index than the classical Newton method and equivalent to the Fernandez-Torres, Tiruneh et al. and McDougall et al. methods [1, 3, 6]. Furthermore, we demonstrate the performance of the new method is significantly better when compared with the established methods.The two well-known iterative methods for finding simple root of nonlinear equations are namely, the classical secant method and the classical Newton method, given by
for an open interval D is a scalar function. The multipoint root-solvers is of great practical importance since it overcomes theoretical limits of one-point methods concerning the convergence order and computational efficiency. In recent years, some modifications of the Newton-type methods for simple root have been proposed and analysed [5] and very little work has been done on the secant-type methods. Therefore, the purpose of this paper is to show further development of the secant-type methods. In addition, we will demonstrate the similarity between the Fernandez-Torres and Tiruneh et al. method. We have found that the efficiency index of new iterative method has a better efficiency index than the classical Newton method and equivalent to the Fernandez-Torres, Tiruneh et al. and McDougall et al. methods [1, 3, 6]. Furthermore, we demonstrate the performance of the new method is significantly better when compared with the established methods.The two well-known iterative methods for finding simple root of nonlinear equations are namely, the classical secant method and the classical Newton method, given by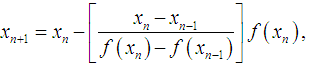
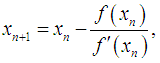
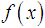 be a real-valued function with a root
be a real-valued function with a root 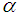 and let
and let 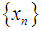 be a sequence of real numbers that converge towards
be a sequence of real numbers that converge towards 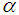 . The order of convergence p is given by
. The order of convergence p is given by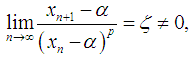
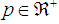 and
and 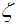 is the asymptotic error constant [2, 5, 7].Definition 2 Let
is the asymptotic error constant [2, 5, 7].Definition 2 Let 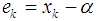 be the error in the kth iteration, then the relation
be the error in the kth iteration, then the relation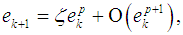
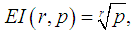
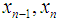 and
and 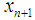 are three successive iterations closer to the root
are three successive iterations closer to the root 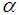 of (1). Then the computational order of convergence may be approximated by
of (1). Then the computational order of convergence may be approximated by 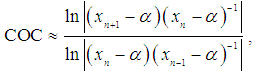
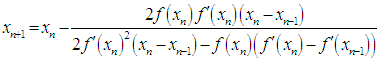
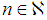 ,
, 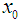 is the initial value and provided that the denominator of (7) is not equal to zero. It is essential to verify our finding and prove the order of convergence of the new iterative method.TheoremAssume that the function
is the initial value and provided that the denominator of (7) is not equal to zero. It is essential to verify our finding and prove the order of convergence of the new iterative method.TheoremAssume that the function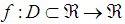 for an open interval D has a simple root
for an open interval D has a simple root 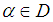 . Let
. Let 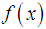 be sufficiently smooth in the interval D. If the initial points
be sufficiently smooth in the interval D. If the initial points 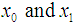 are sufficiently close to
are sufficiently close to 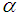 , then the asymptotic convergence order of the new method defined by (7) is
, then the asymptotic convergence order of the new method defined by (7) is 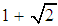 . Proof Let
. Proof Let 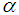 be a simple root of
be a simple root of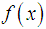 , i.e.
, i.e. 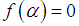 and
and 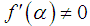 , and the errors at
, and the errors at 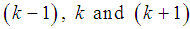 iteration are expressed as
iteration are expressed as 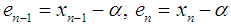 and
and 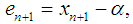 respectively.Using Taylor expansion and taking into account that
respectively.Using Taylor expansion and taking into account that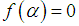 , we have
, we have 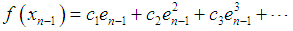
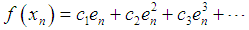
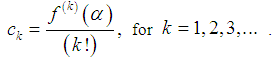
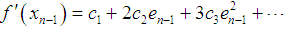
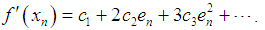
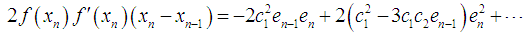
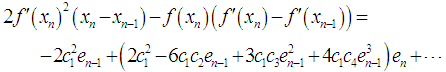
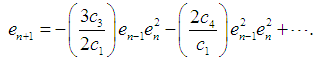
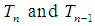 as
as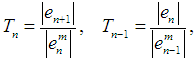
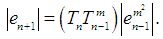
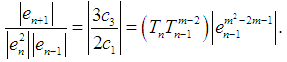
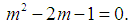
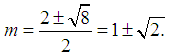
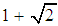 . This completes the proof. The new method (7) requires 2 function evaluations and has the order of convergence
. This completes the proof. The new method (7) requires 2 function evaluations and has the order of convergence 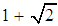 and to determine the efficiency index of the new method, definition 3 shall be used. Hence, the efficiency index of the new iterative method given by (7) is
and to determine the efficiency index of the new method, definition 3 shall be used. Hence, the efficiency index of the new iterative method given by (7) is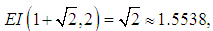
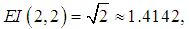
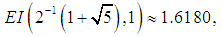
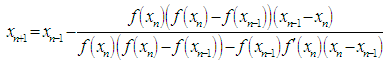
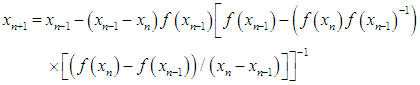
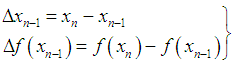
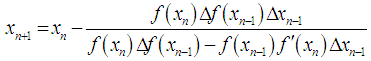
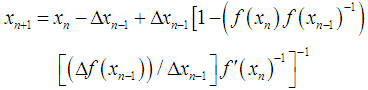
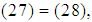 we have
we have 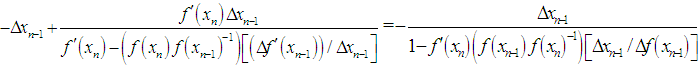
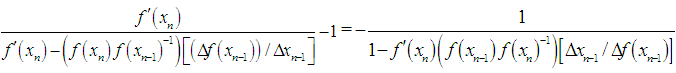
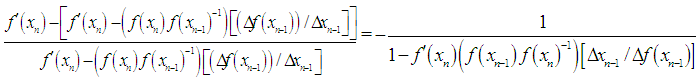
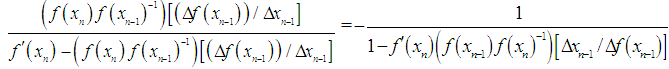
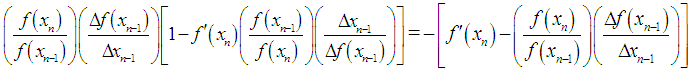
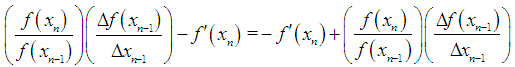
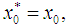
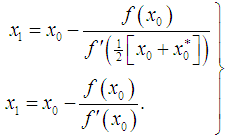
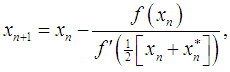
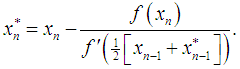
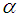 and the approximation
and the approximation 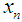 for test function with initial guess
for test function with initial guess 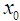 is displayed in tables. Furthermore, the computational order of convergence approximations are displayed in tables and we observe that this perfectly coincides with the theoretical result. The numerical computations listed in the table was performed on an algebraic system called Maple and the errors displayed are of absolute value. The results in the tables were obtained by the following algorithm Algorithm (Maple program) sroots:=[fsolve(f(x),x)]:root1:=sroots[1];diff(f(x),x);x[0]:=x0:dfx[0]:= diff(f(x),x);x[1]:=x[0]-fx[0]/dfx[0]:for n from 1 to 6 dofx[n]:=f(x);dfx[n]:=diff(f(x),x);x1[n]:=x[n]-x[n-1]:dfxx[n]:=dfx[n]-dfx[n-1]:x[n+1]:=evalf(x[n]-(2fx[n]dfx[n]x1[n])/(2dfx[n]^2x1[n]- fx[n]dfxx[n]);new[n]:=root1-x[n];coc:=evalf(ln(new[n]/new[n-1])/(ln(new[n-1]/new[n-2]));print(n,new[n],coc);end:Numerical example 1We will demonstrate the convergence of the new iterative method for the following nonlinear equation
is displayed in tables. Furthermore, the computational order of convergence approximations are displayed in tables and we observe that this perfectly coincides with the theoretical result. The numerical computations listed in the table was performed on an algebraic system called Maple and the errors displayed are of absolute value. The results in the tables were obtained by the following algorithm Algorithm (Maple program) sroots:=[fsolve(f(x),x)]:root1:=sroots[1];diff(f(x),x);x[0]:=x0:dfx[0]:= diff(f(x),x);x[1]:=x[0]-fx[0]/dfx[0]:for n from 1 to 6 dofx[n]:=f(x);dfx[n]:=diff(f(x),x);x1[n]:=x[n]-x[n-1]:dfxx[n]:=dfx[n]-dfx[n-1]:x[n+1]:=evalf(x[n]-(2fx[n]dfx[n]x1[n])/(2dfx[n]^2x1[n]- fx[n]dfxx[n]);new[n]:=root1-x[n];coc:=evalf(ln(new[n]/new[n-1])/(ln(new[n-1]/new[n-2]));print(n,new[n],coc);end:Numerical example 1We will demonstrate the convergence of the new iterative method for the following nonlinear equation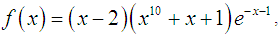
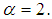 In Table 1 are the errors obtained by the methods described, based on the initial point (IP)
In Table 1 are the errors obtained by the methods described, based on the initial point (IP) 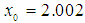 . We observe that the new iterative method is converging to the expected order.
. We observe that the new iterative method is converging to the expected order. 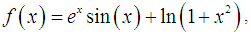
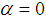 In Table 2 are the errors obtained by the methods described, based on the initial value
In Table 2 are the errors obtained by the methods described, based on the initial value 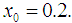
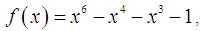
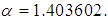 In Table 3 are the errors obtained by the methods described, based on the initial value
In Table 3 are the errors obtained by the methods described, based on the initial value 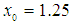 .
. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML


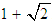 . and its dynamics, Mod. Sim. Eng. 2015 art. ID 502854.
. and its dynamics, Mod. Sim. Eng. 2015 art. ID 502854.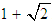 . Appl. Math. Lett. 29 (2014) 20-25.
. Appl. Math. Lett. 29 (2014) 20-25.