-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2018; 8(1): 20-25
doi:10.5923/j.ajcam.20180801.03

New Category of Soft Topological Spaces
Shuker Mahmood Khalil, Mayadah Abd Ulrazaq
Department of Mathematics, College of Science, University of Basrah, Basrah, Iraq
Correspondence to: Shuker Mahmood Khalil, Department of Mathematics, College of Science, University of Basrah, Basrah, Iraq.
| Email: |  |
Copyright © 2018 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this work, we introduce new category of soft topological space is called soft 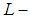 closed topological space, also we study in details the properties of soft
closed topological space, also we study in details the properties of soft 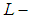 closed space and its relation with soft second-countable space, we state that every soft second-countable space is soft
closed space and its relation with soft second-countable space, we state that every soft second-countable space is soft 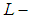 closed but the converse is not true in general, also we describe its relation with soft Lindelof space, soft compact space, and soft absolutely closed space.
closed but the converse is not true in general, also we describe its relation with soft Lindelof space, soft compact space, and soft absolutely closed space.
Keywords:
Soft sets, Soft Lindelof space, Soft compact space, Soft 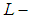 closed space, Soft absolutely closed, Soft second-countable space
closed space, Soft absolutely closed, Soft second-countable space
Cite this paper: Shuker Mahmood Khalil, Mayadah Abd Ulrazaq, New Category of Soft Topological Spaces, American Journal of Computational and Applied Mathematics , Vol. 8 No. 1, 2018, pp. 20-25. doi: 10.5923/j.ajcam.20180801.03.
Article Outline
1. Introduction
- The topological structures of set theories dealing with uncertainties were first discussed by Chang [2]. E. F. Lashin et al. [6] generalized rough set theory in the framework of topological spaces. Shabir and Naz [20] are the first persons who introduce the concept of soft topological spaces which are defined over an initial universe with a fixed parameters. Zorlutuna, et al. [21] introduced some new concepts in soft topological spaces and give some new properties about soft topological spaces. Molodtsov [17] introduced the concept of a soft set as a mathematical tool for dealing with uncertainties. Soft set theory has rich potential for practical applications in several domains. In recently years, soft set theory has been researched in many fields see ([8]-[16]). Compact spaces are one of the most important classes in general topological spaces [3]. They have many well-known properties which can be used in many disciplines. Next, the notion of compact soft spaces around a soft topology is introduced see [21]. Later some other properties of soft topological spaces were also examined: soft countability axioms [19]. In 2017, the notion of soft sequentially absolutely closed space is introduced by S. Mahmood. We introduce in this work the new notation is called soft
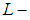 closed space and we prove in this work the soft
closed space and we prove in this work the soft 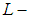 closed space is a soft topological property, also we study its relation with soft Lindelof space, we show that every soft Lindelof spaces is a soft
closed space is a soft topological property, also we study its relation with soft Lindelof space, we show that every soft Lindelof spaces is a soft 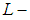 closed space but the converse is not true in general, also we show that every soft space satisfies the soft second axiom of countability that is soft
closed space but the converse is not true in general, also we show that every soft space satisfies the soft second axiom of countability that is soft 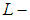 closed space and every soft compact space or soft absolutely closed space is soft
closed space and every soft compact space or soft absolutely closed space is soft 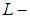 closed space.
closed space.2. Preliminaries
- We now begin by recalling some definitions and some of the basic prosperities of the soft sets.Definition 2.1: ([17])Let
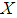 be an initial universe set and let
be an initial universe set and let 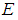 be a set of parameters. A pair
be a set of parameters. A pair 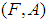 is called a soft set (over
is called a soft set (over 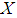 ) where
) where 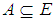 and
and 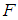 is a multivalued function
is a multivalued function 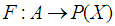 . In other words, the soft set is a parameterized family of subsets of the set
. In other words, the soft set is a parameterized family of subsets of the set 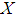 . Every set
. Every set 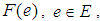 from this family may be considered as the set of e-elements of the soft set
from this family may be considered as the set of e-elements of the soft set 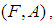 or as the set of
or as the set of 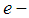 approximate elements of the soft set. Clearly, a soft set is not a set. For two soft sets
approximate elements of the soft set. Clearly, a soft set is not a set. For two soft sets 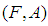 and
and 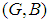 over the common universe
over the common universe 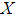 , we say that
, we say that 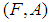 is a soft subset of
is a soft subset of 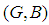 if
if 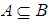 and
and 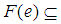
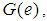 for all
for all 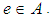 We write
We write 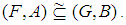
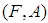 is said to be a soft superset of
is said to be a soft superset of 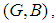 if
if 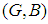 is a soft subset of
is a soft subset of 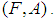 Two soft sets
Two soft sets 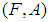 and
and 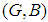 over a common universe
over a common universe 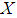 are said to be soft equal if
are said to be soft equal if 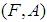 is a soft subset of
is a soft subset of  and
and 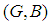 is a soft subset of
is a soft subset of 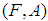 . A soft set
. A soft set 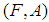 over
over  is called a null soft set, denoted by
is called a null soft set, denoted by 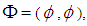 if for each
if for each 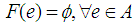 . Similarly, it is called universal soft set, denoted by
. Similarly, it is called universal soft set, denoted by 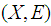 , if for each
, if for each 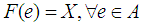 . The collection of all soft sets over a universe
. The collection of all soft sets over a universe 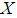 and the parameter set
and the parameter set 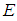 is a family of soft sets denoted by
is a family of soft sets denoted by 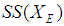 . Also, the collection of all soft sets over a universe
. Also, the collection of all soft sets over a universe 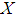 and the parameter set
and the parameter set 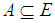 is a family of soft sets denoted by
is a family of soft sets denoted by 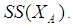 Definition 2.2: ([7]) The union of two soft sets
Definition 2.2: ([7]) The union of two soft sets 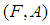 and
and 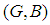 over
over 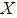 is the soft set
is the soft set 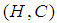 , where
, where 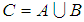 and for all
and for all 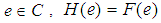 if
if 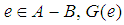 if
if 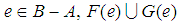 if
if 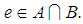 We write
We write 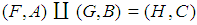 . The intersection
. The intersection 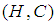 of
of 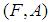 and
and 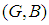 over
over 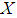 , denoted
, denoted 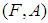
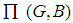 , is defined as
, is defined as 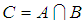 , and
, and 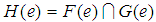 for all
for all 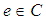 . Definition 2.3: ([21]) The soft set
. Definition 2.3: ([21]) The soft set 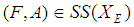 is called a soft point in
is called a soft point in 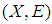 , denoted by
, denoted by 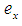 , if there exist
, if there exist 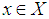 and
and 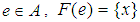 and
and 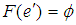 for all
for all 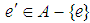 . The soft point
. The soft point 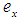 is said to be in the soft set
is said to be in the soft set 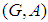 , denoted by
, denoted by 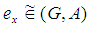 , if for the element
, if for the element 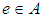 and
and 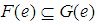 .Definition 2.4: ([20]) The difference
.Definition 2.4: ([20]) The difference 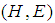 of two soft sets
of two soft sets 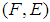 and
and 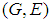 over
over 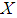 , denoted by
, denoted by 
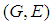 , is defined as
, is defined as 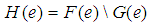 for all
for all 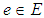 .Definition 2.5: ([20]) Let
.Definition 2.5: ([20]) Let 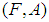 be a soft set over
be a soft set over 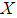 . The complement of
. The complement of 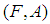 with respect to the universal soft set
with respect to the universal soft set 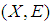 , denoted by
, denoted by 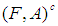 , is defined as
, is defined as 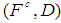 , where
, where 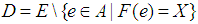
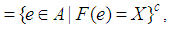 and for all
and for all 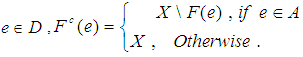 Proposition 2.6: ([20]) Let
Proposition 2.6: ([20]) Let 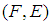 and
and 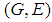 be the soft sets over
be the soft sets over 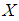 . Then(1)
. Then(1) 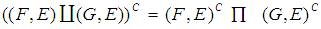 (2)
(2) 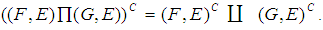 Definition 2.7: ([20])Let
Definition 2.7: ([20])Let  be the collection of soft sets over
be the collection of soft sets over  . Then
. Then 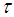 is called a soft topology on
is called a soft topology on 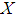 if
if 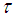 satisfies the following axioms:(i)
satisfies the following axioms:(i) 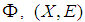 belong to
belong to 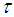 . (ii) The union of any number of soft sets in
. (ii) The union of any number of soft sets in 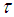 belongs to
belongs to 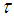 . (iii) The intersection of any two soft sets in
. (iii) The intersection of any two soft sets in 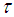 belongs to
belongs to 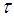 .The triplet
.The triplet 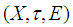 is called a soft topological space over
is called a soft topological space over 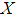 . The members of
. The members of 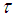 are called soft open sets in
are called soft open sets in 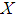 and complements of them are called soft closed sets in
and complements of them are called soft closed sets in 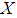 . Definition 2.8: ([4])The soft closure of
. Definition 2.8: ([4])The soft closure of 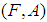 is the intersection of all soft closed sets containing
is the intersection of all soft closed sets containing 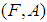 . (i.e) The smallest soft closed set containing
. (i.e) The smallest soft closed set containing 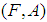 and is denoted by
and is denoted by 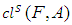 . The soft interior of
. The soft interior of 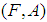 is the union of all soft open set is contained in
is the union of all soft open set is contained in 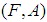 and is denoted by
and is denoted by 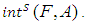 Definition 2.9: ([1]) Let
Definition 2.9: ([1]) Let 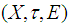 be a soft topological space. A sub-collection
be a soft topological space. A sub-collection 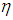 of
of 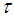 is said to be a base for
is said to be a base for 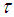 if every member of
if every member of 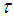 can be expressed as a union of members of
can be expressed as a union of members of 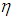 .Definition 2.10: ([1]) Let
.Definition 2.10: ([1]) Let 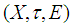 be a soft topological space, and let
be a soft topological space, and let 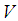 be a family a soft neighborhood of some soft point
be a family a soft neighborhood of some soft point 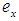 . If, for each soft neighborhood
. If, for each soft neighborhood 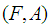 of
of 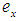 , there exists a
, there exists a 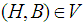 such that
such that 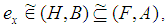 then we say that
then we say that 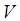 is a soft neighborhoods base at
is a soft neighborhoods base at 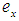 .Definition 2.11: ([18]) A family
.Definition 2.11: ([18]) A family 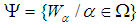 of soft sets is a cover of a soft set (F, A) if
of soft sets is a cover of a soft set (F, A) if 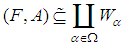 . If each member of
. If each member of 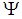 is a soft open set, then
is a soft open set, then 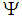 is called a soft open cover.Definition 2.12: ([18]) A soft topological space
is called a soft open cover.Definition 2.12: ([18]) A soft topological space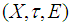 is called soft compact space if each soft open cover of
is called soft compact space if each soft open cover of 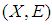 has a finite subcover.Definition 2.14 ([1]) Let
has a finite subcover.Definition 2.14 ([1]) Let 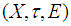 be a soft topological space. Then
be a soft topological space. Then 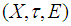 is called soft absolutely closed iff for each soft open cover
is called soft absolutely closed iff for each soft open cover 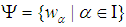 of
of 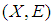 , there exist
, there exist 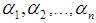 such that
such that 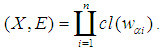 Definition 2.15 ([1]) Let
Definition 2.15 ([1]) Let 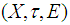 be a soft topological space. If
be a soft topological space. If 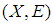 has a countable soft base, then we say that
has a countable soft base, then we say that 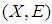 is soft second-countable.Definition 2.16: ([1]) A soft space
is soft second-countable.Definition 2.16: ([1]) A soft space 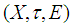 is soft Lindelof if each soft open covering
is soft Lindelof if each soft open covering 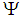 of
of 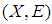 has a countable subcover.Definition 2.17 ([5]) Let
has a countable subcover.Definition 2.17 ([5]) Let 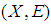 and
and 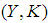 be soft classes and let
be soft classes and let 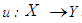 and
and 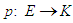 be mappings. Then a mapping
be mappings. Then a mapping 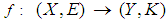 is defined as: for a soft set
is defined as: for a soft set 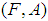 in
in 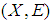 ,
, 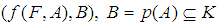 is a soft set in
is a soft set in 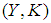 given by
given by 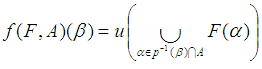 for
for 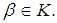
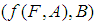 is called a soft image of a soft set
is called a soft image of a soft set 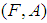 . If B = K, then we shall write
. If B = K, then we shall write 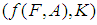 as
as 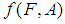 .Definition 2.18 ([5]) Let
.Definition 2.18 ([5]) Let 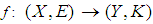 be a mapping from a soft class
be a mapping from a soft class 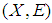 to another soft class
to another soft class 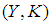 and
and 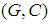 a soft set in soft class
a soft set in soft class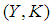 where
where 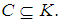 Let
Let 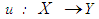 and
and 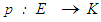 be mappings. Then
be mappings. Then 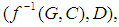
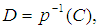 is a soft set in the soft classes
is a soft set in the soft classes 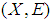 defined as:
defined as: 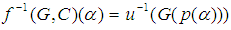 for
for 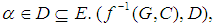 is called a soft inverse image of
is called a soft inverse image of 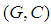 . Hereafter, we shall write
. Hereafter, we shall write 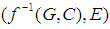 as
as 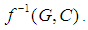 Theorem 2.19 ([5]) Let
Theorem 2.19 ([5]) Let 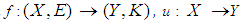 and
and 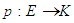 be mappings. Then for soft sets
be mappings. Then for soft sets 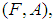
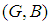 and a family of soft sets
and a family of soft sets 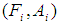 in the soft class
in the soft class 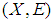 we have:(1)
we have:(1) 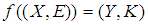 ,(2)
,(2) 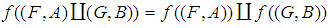 in general
in general 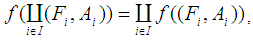 (3)
(3) 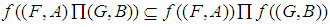 in general
in general 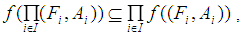 (4) If
(4) If 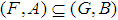 then
then 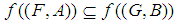 , (5)
, (5) 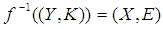 , (6)
, (6) 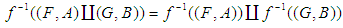 in general
in general 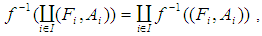 (7)
(7) 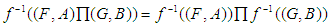 in general
in general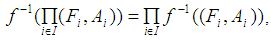 (8) If
(8) If 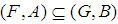 then
then 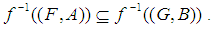 Definition 2.20 ([5]) A soft mapping
Definition 2.20 ([5]) A soft mapping 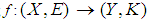 is said to be soft continuous (briefly s-continuous) if the soft inverse image of each soft open set of
is said to be soft continuous (briefly s-continuous) if the soft inverse image of each soft open set of 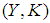 is a soft open set in
is a soft open set in 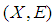 .Definition 2.21 ([5]) A soft mapping
.Definition 2.21 ([5]) A soft mapping 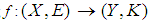 is said to be soft open (briefly s-open) if soft image of each soft open set of
is said to be soft open (briefly s-open) if soft image of each soft open set of 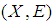 is a soft open set in
is a soft open set in 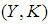 .Definition 2.22 ([5]) A soft mapping
.Definition 2.22 ([5]) A soft mapping 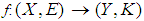 is said to be soft homeomorphism if f is onto and one to one.
is said to be soft homeomorphism if f is onto and one to one.3. Soft Lindelof Closed Space
- Definition 3.1 Let
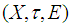 be a topological space we say that
be a topological space we say that 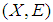 is a soft Lindelof closed space (soft
is a soft Lindelof closed space (soft 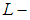 closed space) iff each soft open cover
closed space) iff each soft open cover 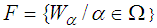 of
of 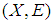 has a soft countable subfamily whose soft closure covers
has a soft countable subfamily whose soft closure covers 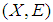 [i.e.
[i.e. 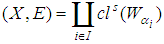 ].Example 3.2 Let
].Example 3.2 Let  be real line, and let
be real line, and let 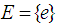 . Then
. Then 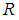 be an uncountable set. Let
be an uncountable set. Let 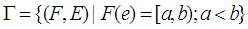 , and let
, and let 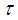 be the soft topology generated by
be the soft topology generated by 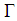 as a base. Hence
as a base. Hence 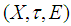 is soft
is soft 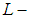 closed space. Indeed, for each soft point
closed space. Indeed, for each soft point 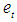 , it is easy to see that
, it is easy to see that 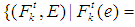
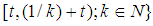 is a soft neighborhoods base at
is a soft neighborhoods base at 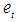 . Let
. Let 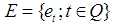 . Thus
. Thus 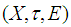 is
is 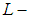 closed space.Theorem: 3.3 If
closed space.Theorem: 3.3 If 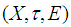 is a soft Lindelof space, then
is a soft Lindelof space, then 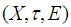 is a soft
is a soft 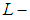 closed space.Proof:Let
closed space.Proof:Let 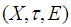 be a soft Lindelof space. Then for each soft open cover
be a soft Lindelof space. Then for each soft open cover 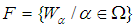 of
of 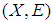 there is a countable sub-collection of
there is a countable sub-collection of 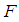 which also covers
which also covers 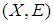 [i.e.
[i.e. 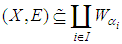 , where
, where 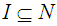 ]. However,
]. However, 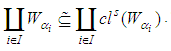 This implies that
This implies that 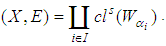 Hence
Hence 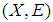 is a soft
is a soft 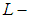 closed space. Remark 3.4: The converse of theorem (3.3) is not true in general. So we will show in following theorem when will be hold. Theorem: 3.5Let
closed space. Remark 3.4: The converse of theorem (3.3) is not true in general. So we will show in following theorem when will be hold. Theorem: 3.5Let 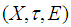 be a soft discrete space. Then
be a soft discrete space. Then 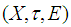 is soft Lindelof space if and only if
is soft Lindelof space if and only if 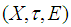 is
is 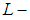 closed.Proof:Assume that
closed.Proof:Assume that 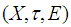 is soft Lindelof space. Then by [theorem (3.3)] we consider that
is soft Lindelof space. Then by [theorem (3.3)] we consider that 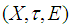 is soft
is soft 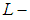 closed space.Conversely, suppose that
closed space.Conversely, suppose that 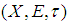 is a soft
is a soft 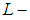 closed space and let
closed space and let 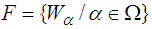 be a soft open cover of
be a soft open cover of 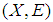 . Then there is a countable sub family whose closure covers
. Then there is a countable sub family whose closure covers 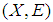 [i.e.
[i.e. 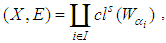 where
where 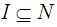 ]. However, for each soft open set in
]. However, for each soft open set in 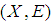 we have
we have 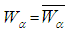 [since
[since 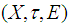 is soft discrete space]. Therefore [
is soft discrete space]. Therefore [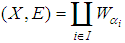 where
where 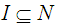 ], Then (X,T) is a soft Lindelof space.Theorem 3.6: Every soft compact space is a soft
], Then (X,T) is a soft Lindelof space.Theorem 3.6: Every soft compact space is a soft 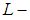 closed space.Proof: Assume that
closed space.Proof: Assume that 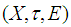 is a soft compact space, then for each soft open cover
is a soft compact space, then for each soft open cover 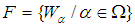 of
of 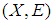 there exists a finite sub-collection of
there exists a finite sub-collection of 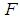 which also covers
which also covers 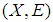 , However, each finite family is countable family. Therefore
, However, each finite family is countable family. Therefore 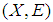 is a soft Lindelof space. Hence
is a soft Lindelof space. Hence 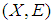 is a soft
is a soft 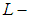 closed space by [Theorem, (3.3)]. Theorem 3.7: Every soft absolutely closed space is a soft
closed space by [Theorem, (3.3)]. Theorem 3.7: Every soft absolutely closed space is a soft 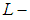 closed space.Proof:Assume that
closed space.Proof:Assume that 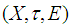 is a soft topological space where
is a soft topological space where 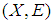 is absolutely closed, let
is absolutely closed, let 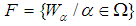 be a soft open cover of
be a soft open cover of 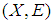 . Then there is a finite sub-collection of whose soft closure covers
. Then there is a finite sub-collection of whose soft closure covers 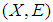 [since
[since 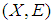 is soft absolutely closed space], thus there is a countable sub-collection of
is soft absolutely closed space], thus there is a countable sub-collection of 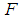 whose soft closure covers
whose soft closure covers 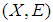 [since each finite family is a countable family]. Then
[since each finite family is a countable family]. Then 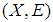 is a soft
is a soft  closed space.Theorem 3.8: If
closed space.Theorem 3.8: If 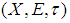 is soft second-countable, then
is soft second-countable, then 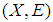 is a soft
is a soft 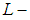 closed space.Proof:Assume that
closed space.Proof:Assume that 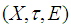 is a soft second-countable, then
is a soft second-countable, then 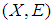 has a countable soft base. Therefore for each soft open cover there is a countable sub-cover of
has a countable soft base. Therefore for each soft open cover there is a countable sub-cover of  . Then
. Then 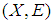 is a soft Lindelof space but by [Theorem, (3,3)] we have
is a soft Lindelof space but by [Theorem, (3,3)] we have 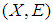 is a soft
is a soft  closed space.Remark 3.9: The converse of the theorem (3, 8) is not true in general.Example 3.10 Let
closed space.Remark 3.9: The converse of the theorem (3, 8) is not true in general.Example 3.10 Let 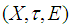 be a soft
be a soft 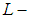 closed topological space in example (3.2) we shall prove that
closed topological space in example (3.2) we shall prove that 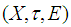 is not soft second-countable. Let
is not soft second-countable. Let 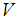 be an arbitrary soft base for
be an arbitrary soft base for 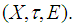 For arbitrary soft point
For arbitrary soft point 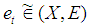 and soft open neighborhood
and soft open neighborhood 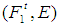 , there exists a soft open set
, there exists a soft open set 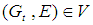 such that
such that 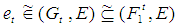 , and hence
, and hence 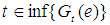 . If
. If 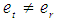 , then
, then 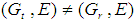 . Therefore, the set
. Therefore, the set 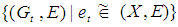 is an uncountable subfamily of
is an uncountable subfamily of 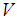 , and thus
, and thus 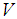 is an uncountable family.Proposition 3.11: A soft
is an uncountable family.Proposition 3.11: A soft 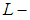 closeness is a topological property.Proof:Assume that
closeness is a topological property.Proof:Assume that 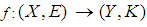 is a soft homeomorphism and
is a soft homeomorphism and 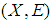 is a soft
is a soft  closed space, we went to show that
closed space, we went to show that 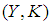 is a soft
is a soft  closed space. Suppose that
closed space. Suppose that 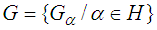 is a soft open cover of
is a soft open cover of 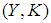 [i.e.
[i.e. 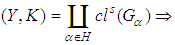
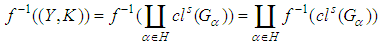 ]. However,
]. However, 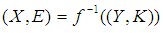 [since
[since 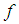 is on to] and since
is on to] and since 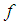 is soft continuous function we have
is soft continuous function we have 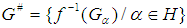 is a soft open cover of
is a soft open cover of 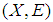 but
but 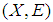 is a soft
is a soft 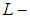 closed space, then there is a countable sub-collection of
closed space, then there is a countable sub-collection of 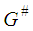 whose soft closure covers
whose soft closure covers 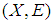 [i.e.
[i.e. 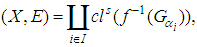 where
where  ], therefore
], therefore 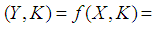
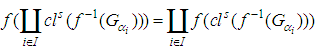
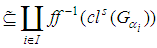
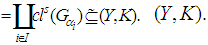 Thus
Thus 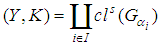 , where
, where 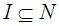 . Then
. Then 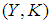 is soft
is soft 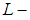 closed space. Theorem 3.12: The cartesian product of countably many soft
closed space. Theorem 3.12: The cartesian product of countably many soft 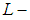 closed spaces is soft
closed spaces is soft 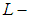 closed.Proof: Let
closed.Proof: Let 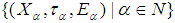 be a family of countable many soft
be a family of countable many soft 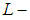 closed spaces. For each
closed spaces. For each 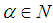 , let
, let 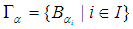 be asoft open cover of
be asoft open cover of 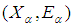 . Then there is a soft countable subfamily of
. Then there is a soft countable subfamily of 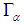 whose soft closure covers
whose soft closure covers 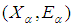 [i.e.
[i.e. 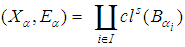 ]. Put
]. Put 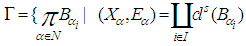 , for countable many values
, for countable many values 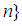 . Hencev
. Hencev 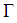 is a countable. Further,
is a countable. Further, 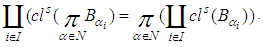 Then for any soft open cover
Then for any soft open cover 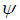 for
for 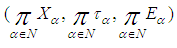 , there is a soft countable subfamily of
, there is a soft countable subfamily of 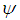 whose soft closure covers
whose soft closure covers 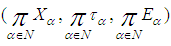 .Remark 3.13: By the above results we have the following diagram:
.Remark 3.13: By the above results we have the following diagram: | Figure 1. Diagram showing relationships among some of the soft spaces |
4. Conclusions
- In this paper, the concept of soft
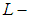 closed spaces is introduced. Further, in this work we describe its relation with soft Lindelof space, soft compact space, and soft absolutely closed space. Assume
closed spaces is introduced. Further, in this work we describe its relation with soft Lindelof space, soft compact space, and soft absolutely closed space. Assume 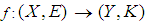 is a soft strongly open map (soft generality open) from
is a soft strongly open map (soft generality open) from 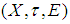 soft
soft 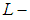 closed space into
closed space into 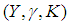 soft countable
soft countable 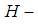 closed space (soft sequentially
closed space (soft sequentially 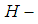 closed space). The question we are concerned with is: what is the possible property of soft map
closed space). The question we are concerned with is: what is the possible property of soft map 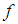 need to provide that
need to provide that 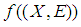 is soft countable
is soft countable 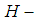 closed (soft sequentially
closed (soft sequentially 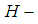 closed) subspace of
closed) subspace of 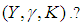
ACKNOWLEDGEMENTS
- The authors would like to thank from the anonymous reviewers for carefully reading of the manuscript and giving useful comments, which will help to improve the paper.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML -Closed sets in Soft Topological Spaces, Journal of Advances in Mathematics, 4(3), 478- 485.
-Closed sets in Soft Topological Spaces, Journal of Advances in Mathematics, 4(3), 478- 485. Algebras of the power sets, International Journal of Applications of Fuzzy Sets and Artificial Intelligence, 7, 231-243.
Algebras of the power sets, International Journal of Applications of Fuzzy Sets and Artificial Intelligence, 7, 231-243.