T. Zhanlav1, Kh. Otgondorj2
1Institute of Mathematics, National University of Mongolia, Mongolia
2School of Applied Sciences, Mongolian University of Science and Technology, Mongolia
Correspondence to: Kh. Otgondorj, School of Applied Sciences, Mongolian University of Science and Technology, Mongolia.
| Email: |  |
Copyright © 2018 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
We propose a new family of optimal eight-order methods for solving nonlinear equations. The order of convergence of proposed methods verified using sufficient convergence conditions given in [6]. Using of sufficient convergence condition allows us to develop new optimal three-point iterations. Various numerical examples are considered to check the performance and to verify the theoretical results. Numerical comparisons of proposed methods with some existing methods are made. The test results are in good accordance with our study.
Keywords:
Nonlinear equations, Iterations methods, Optimal order of convergence
Cite this paper: T. Zhanlav, Kh. Otgondorj, A New Family of Optimal Eighth-order Methods for Solving Nonlinear Equations, American Journal of Computational and Applied Mathematics , Vol. 8 No. 1, 2018, pp. 15-19. doi: 10.5923/j.ajcam.20180801.02.
1. Introduction
At present, there are many optimal eighth-order methods for solving nonlinear equations (see, e.g., [1, 2, 3]). They require complicated convergence analysis that is feasible only by symbolic computation, although they produce high accuracy. The interest for these methods has renewed in recent years due to the rapid development of digital computers, advanced computer arithmetic and symbolic computation. In this note, we develop a family of three-point methods with optimal eighth-order convergence. In Section 2, the new family is developed and its convergence analysis is discussed. Unlike the usually considered convergence analysis here we first time used the sufficient conditions under which the three-point iteration have the eighth order of convergence [7, 8]. This allows to simplify the proof of theorem and to reduce tedious calculations. We also discussed similar theorems given by Sharma and Arora in [4, 5] and by Petrovic et al in [3]. The theoretical results proved in Section 2 are verified in Section 3 by considering various numerical examples. A comparison of the new methods with the existing methods is also given in this section.
2. The Family of Methods
Let 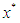 be a simple zero of the function
be a simple zero of the function 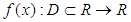 and
and 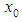 be an initial approximation to
be an initial approximation to 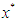 . We consider the following simple three-point iteration
. We consider the following simple three-point iteration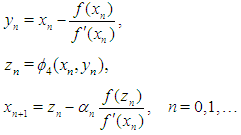 | (1) |
Here 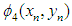 is any two–point optimal fourth order scheme and
is any two–point optimal fourth order scheme and 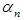 is given by the following formula
is given by the following formula 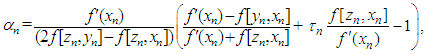 | (2) |
where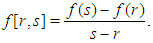 | (3) |
Note that any two–point optimal fourth order iteration can be written as [8]: 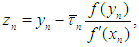 | (4) |
or 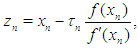 | (5) |
where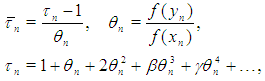 | (6) |
with some constants 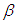 and
and 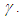 Theorem 1 Let the function
Theorem 1 Let the function 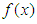 be sufficiently differentiable in a neighborhood of its simple zero
be sufficiently differentiable in a neighborhood of its simple zero 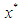 and
and 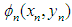 is an optimal fourth order method. If the initial approximation
is an optimal fourth order method. If the initial approximation 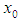 is sufficiently close to
is sufficiently close to 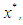 then the order of convergence of iteration (1), (2) is 8. Proof Using (1), (6) we have
then the order of convergence of iteration (1), (2) is 8. Proof Using (1), (6) we have 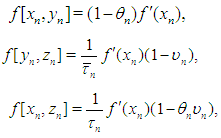 | (7) |
where 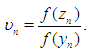 | (8) |
Substituting (7) and (8) into (2) we get 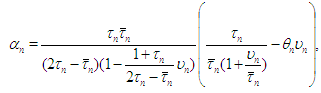 | (9) |
Using the well-known expansion 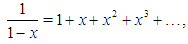 | (10) |
One can write (9) as 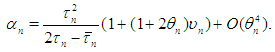 | (11) |
Since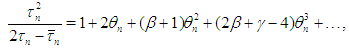 then from (11), we obtain
then from (11), we obtain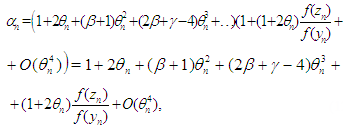 | (12) |
in which we have used 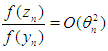 . Then by Theorem 1 and 2 in [7, 8] the order of convergence of (1) and (2) is 8.It is often used two-point iterations (5) with functions [1-5]
. Then by Theorem 1 and 2 in [7, 8] the order of convergence of (1) and (2) is 8.It is often used two-point iterations (5) with functions [1-5] 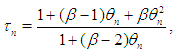 | (13) |
and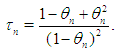 | (14) |
In [10] it was developed optimal fourth–order method with parameter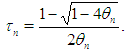 | (15) |
According to (15) we call the iteration (1), (2) with (15) the eighth–order iteration based on Zhanlav’s fourth-order method. Similar theorems for (1) presented by Sharma and Arora in [4, 5] under choices 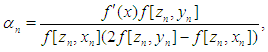 | (16) |
and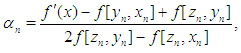 | (17) |
and by Petkovic et al in [3] under choice 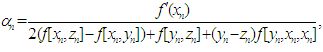 | (18) |
where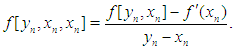 Now we consider the three-point iterations (1) with
Now we consider the three-point iterations (1) with 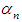 given by formula
given by formula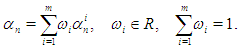 | (19) |
Here by 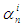 we denote any functions satisfying the condition (12). In particular, as
we denote any functions satisfying the condition (12). In particular, as 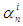 one can take functions (2), (16), (17) and (18). As before, using the sufficient convergence conditions (12) it is easy to prove that the convergence order of three–point iterations (1) with
one can take functions (2), (16), (17) and (18). As before, using the sufficient convergence conditions (12) it is easy to prove that the convergence order of three–point iterations (1) with 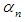 given by (19) is 8.
given by (19) is 8.
3. Numerical Experiments
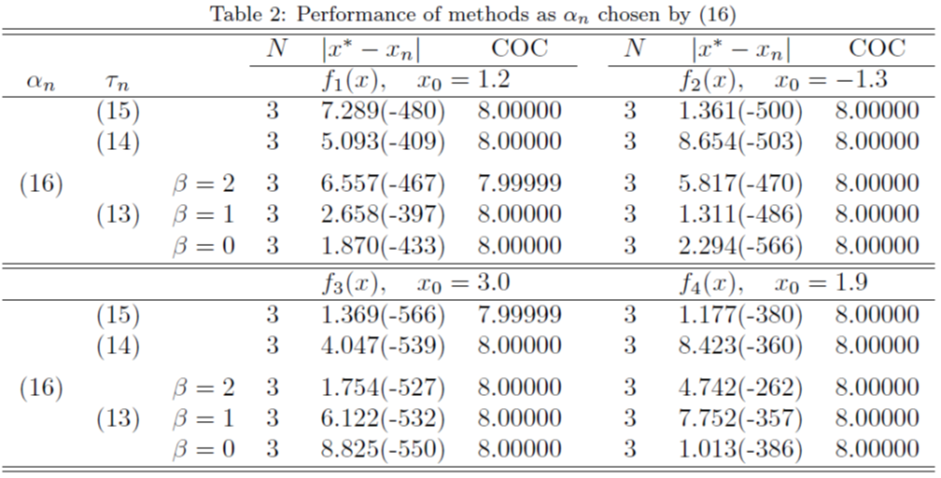
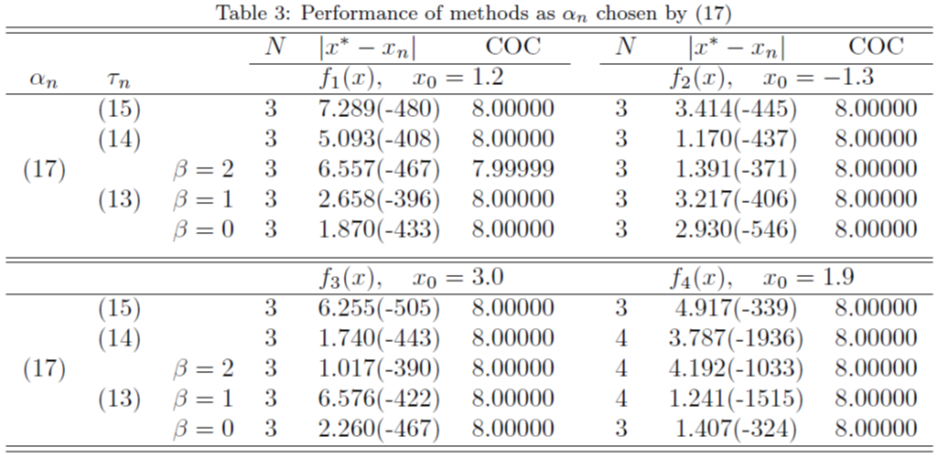
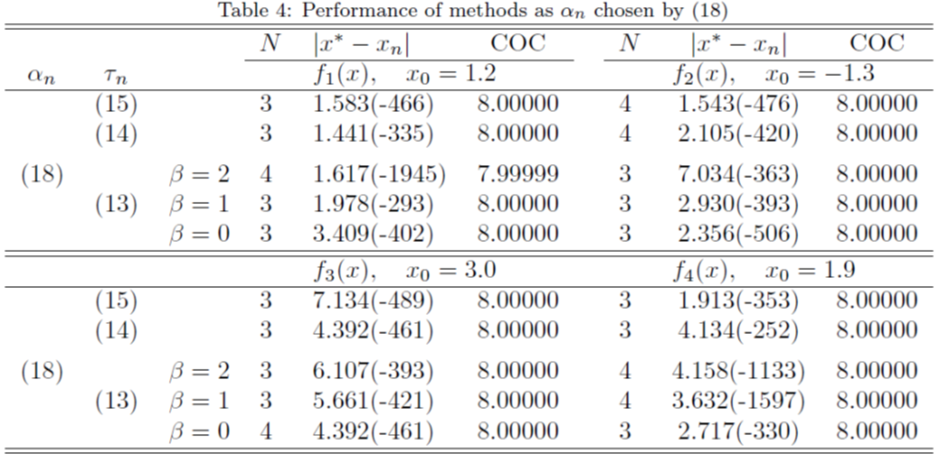
In this section, we have made some numerical experiments on our proposed method and given some numerical comparisons with existing optimal eighth order methods as various examples. We consider the following test functions used in [5, 6]: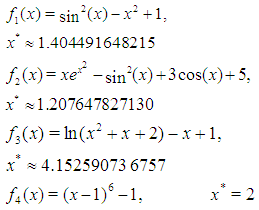 All computations have been carried out using Maple 18 computer algebra system with 1500 significant digits and the fixed stopping criterion
All computations have been carried out using Maple 18 computer algebra system with 1500 significant digits and the fixed stopping criterion 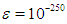 . In Tables 1-4,
. In Tables 1-4, 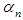 and
and 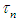 with some parameters are considered in first and in second columns, respectively. The number of iterations
with some parameters are considered in first and in second columns, respectively. The number of iterations 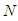 , the absolute value
, the absolute value 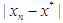 and the computational order of convergence (COC) are displayed in theseTables as well. To verify the theoretical order of convergence of our methods, we calculate the computational order of convergence using the formula [6]
and the computational order of convergence (COC) are displayed in theseTables as well. To verify the theoretical order of convergence of our methods, we calculate the computational order of convergence using the formula [6]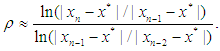 For a comparison, we employed the Sharma-Arora methods with function (16), (17) and method given in [3] with function (18). From Tables 1-4, we see that the COC perfectly coincides with theoretical order and the new method (1), (2) with function (15) is comparable with existing methods.
For a comparison, we employed the Sharma-Arora methods with function (16), (17) and method given in [3] with function (18). From Tables 1-4, we see that the COC perfectly coincides with theoretical order and the new method (1), (2) with function (15) is comparable with existing methods.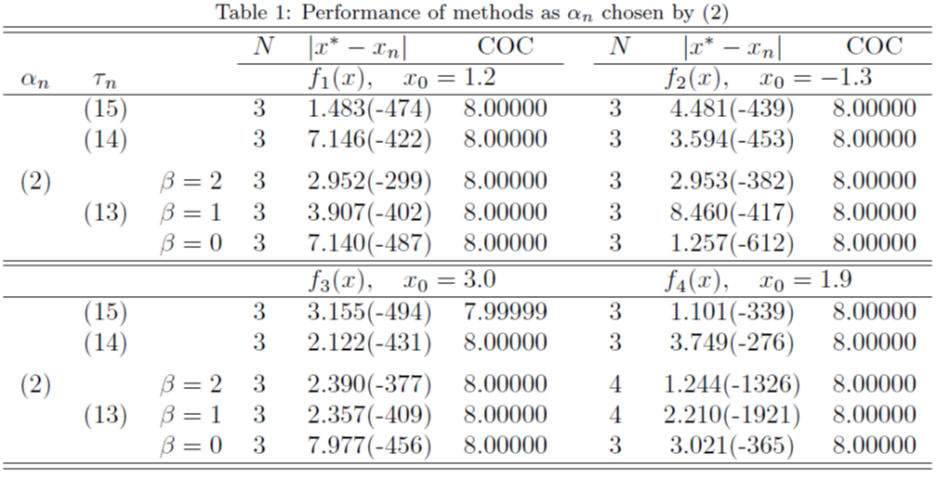 | Table 1 |
 | Table 2 |
 | Table 3 |
 | Table 4 |
4. Conclusions
In this paper, a new family of optimal eight--order methods for solving nonlinear equations is introduced and studied. This family (1), (19) includes the three--point methods given by Sharma and Arora in [4, 5] and by Petkovic et al in [3] and our proposed method (1), (2) as particular cases. Finally, the theoretical proofs and numerical experiments have shown that new iterative method is of eight-order and effective.
ACKNOWLEDGEMENTS
This work was supported by the Foundation of Science and Technology of Mongolian under grant SST_007/2015.
References
| [1] | C. Chun, B. Neta, Comparative study of eighth-order methods for finding simple roots of nonlinear equations, Numer. Algor. 74 (2017) 1169-1201. |
| [2] | Chun, C. & Neta, B. On the new family of optimal eighth order methods developed by Lotfi et al. Numer Algor (2016) 72: 363. |
| [3] | M.S. Petkovic, B. Neta, L.D. Petkovic, J. Dzunic, Multipoint Methods for Solving Nonlinear Equations, Elsevier, 2013. |
| [4] | M.S. Petkovic, B. Neta, L.D. Petkovic, J. Dzunic, Multipoint Methods for Solving Nonlinear Equations, A survey. Appl. Math. Comput. 226 (2014) 635-660. |
| [5] | J.R. Sharma, H. Arora, A new family of optimal eighth order methods with dynamics for nonlinear equations, Appl. Math. Comput. 273 (2016) 924-933. |
| [6] | J.R. Sharma, H. Arora, An efficient family of weighted-Newton methods with optimal eighth order convergence, Appl. Math. Lett. 29 (2014) 1-6. |
| [7] | X. Wang, L. Liu, Modified Ostrowski's method with eighth-order convergence and high efficiency index, Appl. Math. Lett. 23 (2010) 549-554. |
| [8] | T. Zhanlav, O. Chuluunbaatar, V. Ulziibayar, Generating function method for constructing new iterations, Appl. Math. Comput. 315 (2017) 414-423. |
| [9] | T. Zhanlav, O. Chuluunbaatar, V. Ulziibayar, The necessary and sufficient conditions for some two and three--point Newton's type iterations, Comput Math. Math. Phys. 57 (2017) 1090--1100. |
| [10] | T. Zhanlav, V. Ulziibayar, Modified King's Methods with Optimal Eighth-order of Convergence and High Efficiency Index, American Journal of Comput and Applied Math.6(5) (2016) 177-181. |
| [11] | T. Zhanlav, O. Chuluunbaatar, V. Ulziibayar, Accelerating the convergence of Newton-type iterations, J. Numerical analysis and approximation theory. 46 (2) (2017) 162–180. |


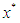 be a simple zero of the function
be a simple zero of the function 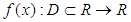 and
and 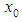 be an initial approximation to
be an initial approximation to 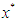 . We consider the following simple three-point iteration
. We consider the following simple three-point iteration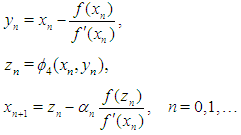
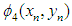 is any two–point optimal fourth order scheme and
is any two–point optimal fourth order scheme and 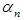 is given by the following formula
is given by the following formula 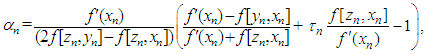
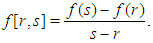
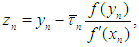
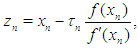
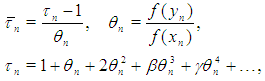
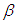 and
and 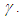 Theorem 1 Let the function
Theorem 1 Let the function 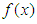 be sufficiently differentiable in a neighborhood of its simple zero
be sufficiently differentiable in a neighborhood of its simple zero 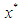 and
and 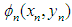 is an optimal fourth order method. If the initial approximation
is an optimal fourth order method. If the initial approximation 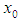 is sufficiently close to
is sufficiently close to 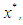 then the order of convergence of iteration (1), (2) is 8. Proof Using (1), (6) we have
then the order of convergence of iteration (1), (2) is 8. Proof Using (1), (6) we have 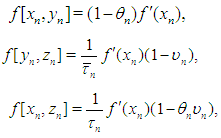
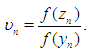
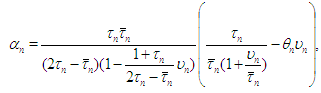
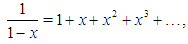
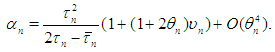
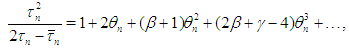 then from (11), we obtain
then from (11), we obtain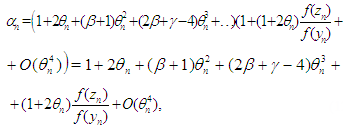
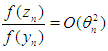 . Then by Theorem 1 and 2 in [7, 8] the order of convergence of (1) and (2) is 8.It is often used two-point iterations (5) with functions [1-5]
. Then by Theorem 1 and 2 in [7, 8] the order of convergence of (1) and (2) is 8.It is often used two-point iterations (5) with functions [1-5] 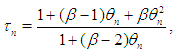
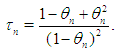
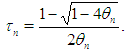
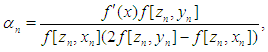
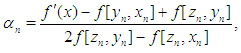
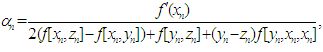
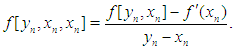 Now we consider the three-point iterations (1) with
Now we consider the three-point iterations (1) with 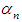 given by formula
given by formula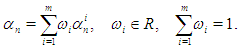
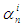 we denote any functions satisfying the condition (12). In particular, as
we denote any functions satisfying the condition (12). In particular, as 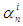 one can take functions (2), (16), (17) and (18). As before, using the sufficient convergence conditions (12) it is easy to prove that the convergence order of three–point iterations (1) with
one can take functions (2), (16), (17) and (18). As before, using the sufficient convergence conditions (12) it is easy to prove that the convergence order of three–point iterations (1) with 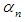 given by (19) is 8.
given by (19) is 8.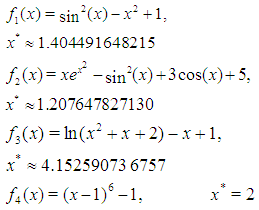 All computations have been carried out using Maple 18 computer algebra system with 1500 significant digits and the fixed stopping criterion
All computations have been carried out using Maple 18 computer algebra system with 1500 significant digits and the fixed stopping criterion 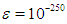 . In Tables 1-4,
. In Tables 1-4, 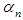 and
and 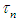 with some parameters are considered in first and in second columns, respectively. The number of iterations
with some parameters are considered in first and in second columns, respectively. The number of iterations 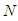 , the absolute value
, the absolute value 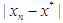 and the computational order of convergence (COC) are displayed in theseTables as well. To verify the theoretical order of convergence of our methods, we calculate the computational order of convergence using the formula [6]
and the computational order of convergence (COC) are displayed in theseTables as well. To verify the theoretical order of convergence of our methods, we calculate the computational order of convergence using the formula [6]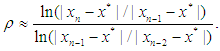 For a comparison, we employed the Sharma-Arora methods with function (16), (17) and method given in [3] with function (18). From Tables 1-4, we see that the COC perfectly coincides with theoretical order and the new method (1), (2) with function (15) is comparable with existing methods.
For a comparison, we employed the Sharma-Arora methods with function (16), (17) and method given in [3] with function (18). From Tables 1-4, we see that the COC perfectly coincides with theoretical order and the new method (1), (2) with function (15) is comparable with existing methods.



 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML